汽车电控单元仿真软件设计与实现
田宏远,谭火彬,梅雅淇
(北京航空航天大学 软件学院,北京 100191)
0 引言
随着新能源汽车的发展,仿真软件逐渐成为新能源汽车研发与生产过程中不可缺少的工具,并逐渐主导着研发流程[1]。新能源汽车仿真涉及整车、电控逻辑、空气动力学和热力学等多个领域,包含了物理性质、行为表现等多个维度。汽车电控单元(Electronic Control Unit,ECU)是指汽车内部各个系统的控制模块,比较典型的有新能源汽车的电池充放电控制单元。本文将聚焦于汽车电控单元系统行为仿真,重点讨论如何从零开始构建一个领域系统的仿真软件。
1 相关工作
在电控单元仿真领域,既有成熟的商用软件Simulink,又有开源的如SciLab 内的Xcos 软件,这些软件都采用图形界面建模,并内置了多种求解器进行求解仿真。功能更为强大的Simulink 还支持代码生成,将模型转化为实际的代码,以便作进一步验证[2]。Simulink 通常用于系统级别的设计和仿真,尤其是控制系统,可以对物理硬件、嵌入式软件、算法和系统运行环境组成的复杂虚拟系统进行仿真[3]。此外,对于需要进行上位机验证的系统,还可以生成嵌入式代码进行后续的测试与验证[4]。在建模语言方面,Modelica 是一个基于方程的面向对象的计算机语言,支持跨领域复杂物理系统的建模,例如机械、电子以及面向过程的子模型系统[5]。Modelica 采用数学方程式的形式描述各个领域的物理现象和规律,并根据系统拓扑结构和语言内在关联对模型进行集成,并通过对微分方程或代数方程的求解实现仿真运算[6]。
用户在使用上述软件时会面临3 个主要问题:①软件安装过程繁琐,仅使用软件的部分功能却要对软件进行全量安装;②软件对于安装机器的性能配置要求高,增加了用户的硬件成本;③仿真流程不透明,很难针对用户的特定需求进行适应性二次开发和模型库扩展。
为此,本文提出基于B/S 架构、系统建模语言(Systems Modeling Language,SysML)与因果框图(Causal Block Diagram,CBD)的建模仿真设计方案以解决上述问题,并实现了一套易于拓展的仿真流程,方便用户进行二次开发和拓展。
2 相关理论
2.1 因果框图
因果框图(Causal Block Diagram,CBD)是一种通过不同形状的图形和连接线来表示模块间依赖关系的数据结构[7],线条所表示的数据依赖关系也可以用来表示数据的流动方向。图1 表示一个简单的CBD,由A、B、C、D 4 个基础模块组成。从依赖关系的角度来看,依赖关系与连线箭头的方向相反,A 不依赖于任何模块,B 依赖于A,C 依赖于A 和B,D 依赖于B 和C;从数据流动的角度来看,数据从A流出,到达B 和C,又从B 流向C,最后从B 和C 一起汇入D。
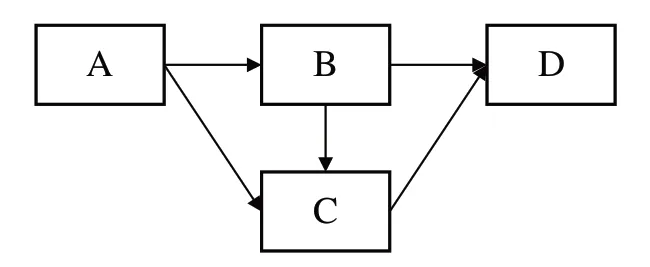
Fig.1 Example of CBD图1 CBD示例
与数据结构中图的定义类似,指向模块的线的数量称为该模块的入度,从该模块指出的线的数量称为该模块的出度。入度为0 的模块即为整个模型的输入,称为输入模块;出度为0 的模块即为整个模型的输出,称为输出模块。入度和出度均不为0的模块称为功能模块。
CBD 最早来自于电路领域,不同的形状框可以代表不同的电路元件,有着不同功能。线条则代表导线,象征着电流的流动方向。电路图本身也是一种对实体电路的建模,当电源施加不同参数时,将相应的电学元件表现出的输出用来表征电路系统的行为,其实就是一个典型的仿真建模过程[8]。
为了进行层次化的系统建模,CBD 中也引入了分层的概念。CBD 中的一个模块可以是由若干其他模块和连线组成的子图,子图中的子模块间也存在着依赖关系,整个子图又在外层中与其他模块形成依赖关系。图2 给出了一个含有层次关系的CBD。其中,B 模块由一个子图组成,子图中B3依赖于B2,B2依赖于B1。而在整个CBD 中,C 依赖于B,B 依赖于A。因此,B1、B2 和B3 均依赖于A,C依赖于B1、B2 和B3。这种层次关系建模可以丰富模型的表达能力,支持将系统分解为子系统,为复杂系统建模提供了解耦和抽象功能。
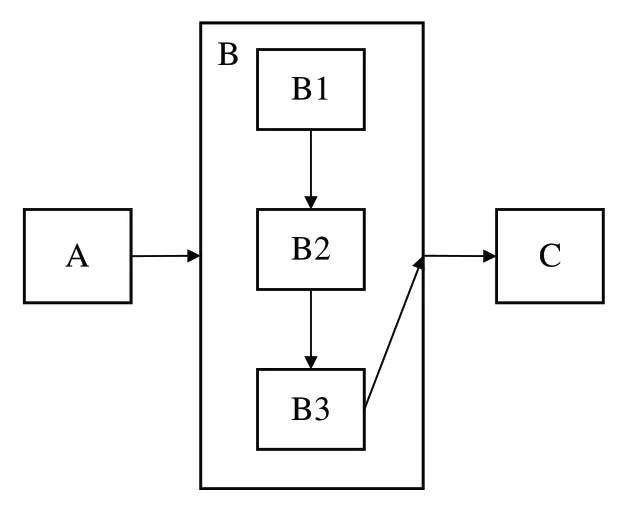
Fig.2 CBD with layers图2 含有层次的CBD
利用CBD 可以完成系统的建模,在下一节中,本文将为静态图赋予语义,使其能够实现动态的仿真功能。
2.2 离散事件系统仿真
离散事件系统(Discrete Event System,DEV)是指一种离散状态、事件驱动的系统,其状态演变完全取决于时间上异步离散事件的发生。DEV 仅由离散状态空间和事件驱动状态转换机制组成[9]。离散事件系统尝试用一个个时间点和状态的变化去描述一个系统,在一个特定的时刻,每个基本模块都有自己所处的状态,并有相应的状态变化函数,用于计算该模块下一时刻所处的状态。
仿真模型由一个个基础仿真模块通过连接组成。使用CBD 和SysML 表示离散事件系统,需要定义好基础模块图的指称语义(Denotational Semantics)和操作语义(Operational Semantics)。指称语义即为每个基础模块定义计算公式;操作语义即指定基础模块的计算顺序,计算序列按顺序计算指称语义中定义的各个公式的值,得到最终的仿真结果。
指称语义的定义因不同的领域需求而有所不同。以电控仿真领域为例,通常需要为加法器、积分器、增益器等常见基础仿真模块定义指称语义。每个基础模块含有输入和输出端口,模块从输入端口获取数据后,经指称语义计算后,由输出端口输出。连线用来连接两个基础仿真模块的输入和输出,连线两端的数据是相同的。特别的,不含输入端口的模块称为输入模块,是整个模型的输入;不含输出端口的模块称为输出模块,是整个模型的输出。
模型图通常可以经过处理后转化为一个有向无环图。对于含有数据依赖关系的有向无环图[10],可以采用拓扑排序的方法得到模块的先后顺序,该先后顺序就是指称语义的计算顺序。拓扑排序的思想是从入度为零的节点开始(对应于CBD 中的输入模块),断开其与节点的连线,并将这些入度为零的节点添加到结果列表中,标识为已排序,然后去寻找图中入度为零的节点,以此类推,直至所有节点都被访问过。由于图中没有圈的存在,因此算法执行到最后一定能访问完所有节点。
如图3 所示,图的入度为零的模块(即输入模块)是A,出度为零的模块(即输出模块)是E。拓扑排序算法首先从A 开始,删除其指向B 和C 的连线,并将A 加入已排序的结果列表sorted。之后,B 模块为唯一入度为零的模块,算法访问B 模块,删除其指向C 和D 的连线,并将B 加入已排序的结果列表。以此类推,算法执行完毕后得到图的拓扑排序结果为[A,B,C,D,E],且已遍历完所有模块。
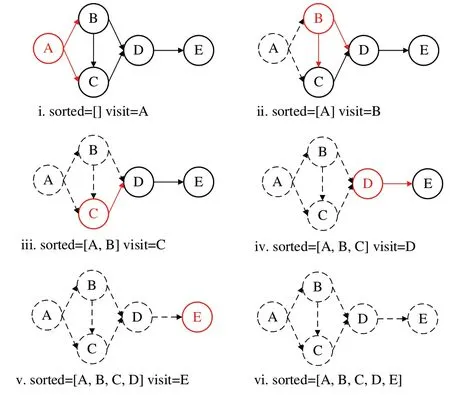
Fig.3 Example of topological sort图3 拓扑排序示例
操作语义所要完成的工作就是对于拓扑排序后的结果列表,在每个时间步内逐一遍历并执行相应模块的指称语义。下面将以伪代码的形式描述操作语义指导下的指称语义计算过程,如算法1所示。
算法1 离散事件系统仿真算法
输入:表示模型的有向无环图G,仿真时长T,仿真步长step
输出:仿真结果
2.3 连续事件系统仿真
在连续事件系统仿真中,需要对连续时间和状态进行建模与仿真,此时则需要引入新的描述形式——微分方程系统(Differential Equation System,DES)[12]。使用微分方程进行系统建模时,并不会通过状态转移函数来计算下一时刻模块的状态变化,而是通过导函数的形式给出状态的变化率来描述状态如何变化。在给定状态值和时间段的情况下,任意时刻的状态值需要根据导函数来计算。可以采取数值积分的方法对连续事件系统的状态进行求解,学界对此已有很多研究,例如欧拉法、龙格库塔(Runge-Kutta)法(根据不同情况分为多种阶数,常见的有二阶和四阶)[11]。
2.4 代数环
代数环(algebraic loop)[13]是指CBD 中模块之间的依赖关系构成一个环,即形成模块间的循环依赖。具体地,在仿真模型中,如果一个模块的值取决于另一个模块的值,而该模块的值又依赖于第一个模块的值,则会形成一个代数环[14]。这会导致仿真系统无法求解变量的值,因为每个模块都需要已知其它模块的值才能计算出自己的值,类似于操作系统中的“死锁”。
图4 展示的即是建模过程中产生的一个代数环。其中,G 是一个增益模块,目的是将输入放大为原来的2 倍后输出。图中明显形成了一个圈回路。要想计算C 的值,就需要先计算C 的增益与2 相加后的结果,从而造成了循环依赖。从数学形式上,可以通过解方程得到C 的值为-2。但是如果放入到仿真流程中,经过一圈的计算,还是回到了C 的输出上,仅凭语句无法直接得出C 的值,除非经过进一步的数学推理(即方程求解)。
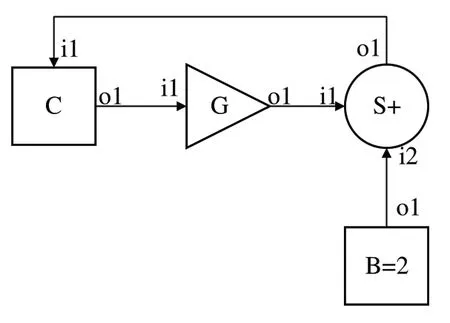
Fig.4 Example of algebraic loop图4 代数环示例
如前文所述,CBD 表达了模块间数据的依赖性,因此可以采用拓扑排序的方式对基础模块进行排序[15],得到的顺序就是正确的计算顺序。然而,由于代数环的存在,用户建立好的CBD 模型并不能直接用于拓扑排序,而是需要经过一定的特殊处理,这种处理被称为代数环的消解。
关于代数环的消解,目前学界有多种解决办法,最常用的就是将代数环转化为数学方程的形式进行矩阵运算求解[16]。但并非所有形式的代数环均有解,因此在建模过程中要尽可能避免代数环的出现。
然而,并非所有在模型中出现的圈都是代数环。在CBD 模型中,当存在回路并且回路中不存在非直接馈通模块(non-direct feedthrough block)时,才会出现代数环。非直接馈通模块是指模块无需知道输入信号即可计算当前时间步的输出,通常维护一个state 变量来存储过往的计算值直接输出,典型的非直接馈通模块有积分模块(Integrator)和单位时延模块(Unit Delay)。因此,在环路中可以断开所有连接到非直接馈通模块的连线,使得环路断开,此时则不再有代数环的问题,如图5所示。
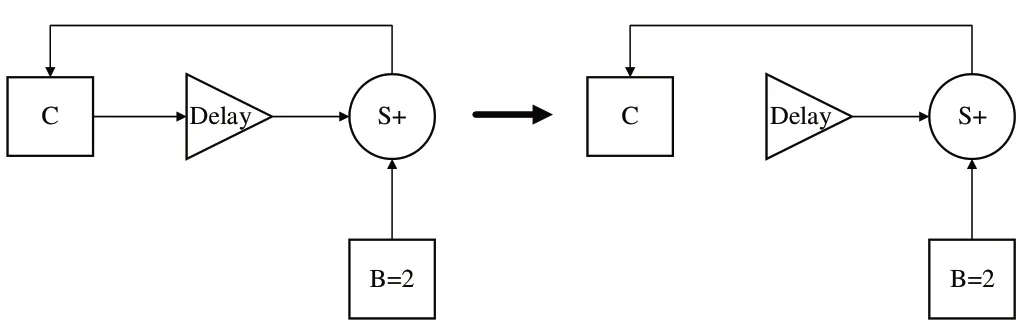
Fig.5 Breaking loop according to non-direct feedthrough module图5 根据非直接馈通模块断开环路
3 仿真系统设计
用户使用建模仿真软件进行系统建模仿真的一个完整流程如图6 所示。首先用户在建模端进行相应的模型搭建,并设定好仿真参数(如仿真时长、仿真步长等);然后建模端会以JSON(JavaScript Object Notation)文件的形式将模型保存,并发送到仿真端;仿真端接收到文件后,则进行相应的仿真运行操作。仿真器将根据用户设置的参数运行模型。在运行时,会判断当前时间步是否到达仿真时长,如果没有到达则继续进行仿真运算;如果到达,则视为仿真完成。运行完成后将结果返回给建模端进行可视化展示和数据下载。从提交仿真模型直至仿真结束所涉及的全部过程称为仿真阶段。本文软件关注的就是仿真阶段的全部功能。

Fig.6 Flow of modeling and simulating图6 建模仿真流程
3.1 软件总体设计
软件采取分层架构,根据功能自顶向下分为数据交互层、数据解析层和仿真运算层。软件体系结构如图7所示。
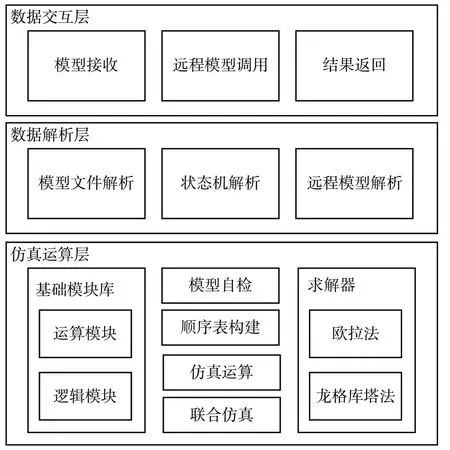
Fig.7 Software architecture图7 软件体系结构
数据交互层主要负责模型接收和远程模型调用,以及仿真结果的返回。接收到的数据将交给数据解析层,将结果返回给建模端进行展示。
数据解析层主要负责解析数据交互层接收到的数据,包括将模型文件解析为内存中的对象、状态机语句值计算以及远程模型文件解析。解析后的模型信息将传给下一层仿真运算层进行仿真计算。
最底层是仿真运算层,也是整个仿真工具的核心。在这一层中,首先需要有基础模块库支撑整个模型的搭建和仿真运行。其次,需要求解器支持连续模型的方程求解,即数值积分计算。当模型被解析完成后,会通过顺序表构建、模型自检进行仿真运行前的准备,之后即可运行仿真。如果涉及联合仿真,将会与其他模型进行数据交互,实现模型之间的同步运行。后文将重点关注仿真运算层的设计与实现。
3.2 基础模块库设计
基础模块库是支撑建模与仿真的基础。基础模块是指参与建模的最基本的计算单元(对应CBD 中的模块),基础模块间通过有方向的连接线的连接构成模型图[17]。
所有基础模块都具有相似的一部分功能和属性,也有其自身的特点,因此可以使用接口的形式将公共的功能抽象出来。
对于模块共有的属性,可以采取继承父类子类的形式将共有属性传递到每个子类中,或者选择组合的方式——即持有该公共属性实例,作为字段出现在其他类中来实现公共属性的统一管理。图8 是所有模块公共属性抽象出的共有结构体BasicProperty,拥有编号id、组件名name 和是否启用enable 3个属性。

Fig.8 Class diagram of public basic property图8 公共基本属性类图
所有基本操作方法组成的特征称为BasicOperation,如图9 所示。具体方法主要包括:①获取模块类型:用来判断模块属于哪一类;②获取模块的输出值:类型是Value,可能是矩阵,也可能是一个单值;③模块自检:用来检查模块是否满足仿真规范;④模块更新:用来更新模块状态值或输出值;⑤模块重置:用来重制并清空模块历史状态信息;⑥获取连接数:用来获取有多少其他模块连接到当前模块,即有多少输入端口;⑦获取第i 个输入端值:用来获取连接到当前模块的第i 个模块的输出值(当前状态值);⑧连接:用来将一个模块连接到当前模块。此外,还有用来判断模块是否是离散模块以及直接馈通模块的方法。

Fig.9 Class diagram of public basic operation图9 公共方法组成的特征类图
对于每一个具体模块,可以定义其结构体,并为该结构体实现BasicOperation 接口,同时将BasicProperty 作为该结构体的属性字段。对于模块自身特有的行为和属性,也可以为该模块的结构体增添相应的属性字段和方法。
对于模型中的每一个基础模块,完成实例化之后,需要存储在一个集合中供仿真器访问运行。然而,每一个基础模块都是一个不同的结构体,如何使用一个集合类型存储不同的结构体类型是一个重要问题。在面向对象的语言中,可以考虑采用多态的形式——父类类型(或接口类型)指向子类实例的方式,以使用一种类型代表多种不同类型[18]。
3.3 仿真流程框架
离散与连续事件的仿真计算是指根据拓扑排序得到的基础模块排序序列依次遍历每个基础模块,根据模块的性质进行离散状态更新或连续数值积分计算的过程。后文将针对这两种计算的特点进行详细介绍。
仿真计算阶段的计算流程如图10 所示。在仿真计算阶段,仿真器将根据模型提供的信息,从用户指定的开始时间到结束时间内,以固定间隔连续计算系统的状态和输出。计算模型状态和输出的这些连续时间点即称为时间步,时间步之间的间隔称为步长。步长可以取决于很多因素,如求解器类型、过零检测[19]和采样时间等。
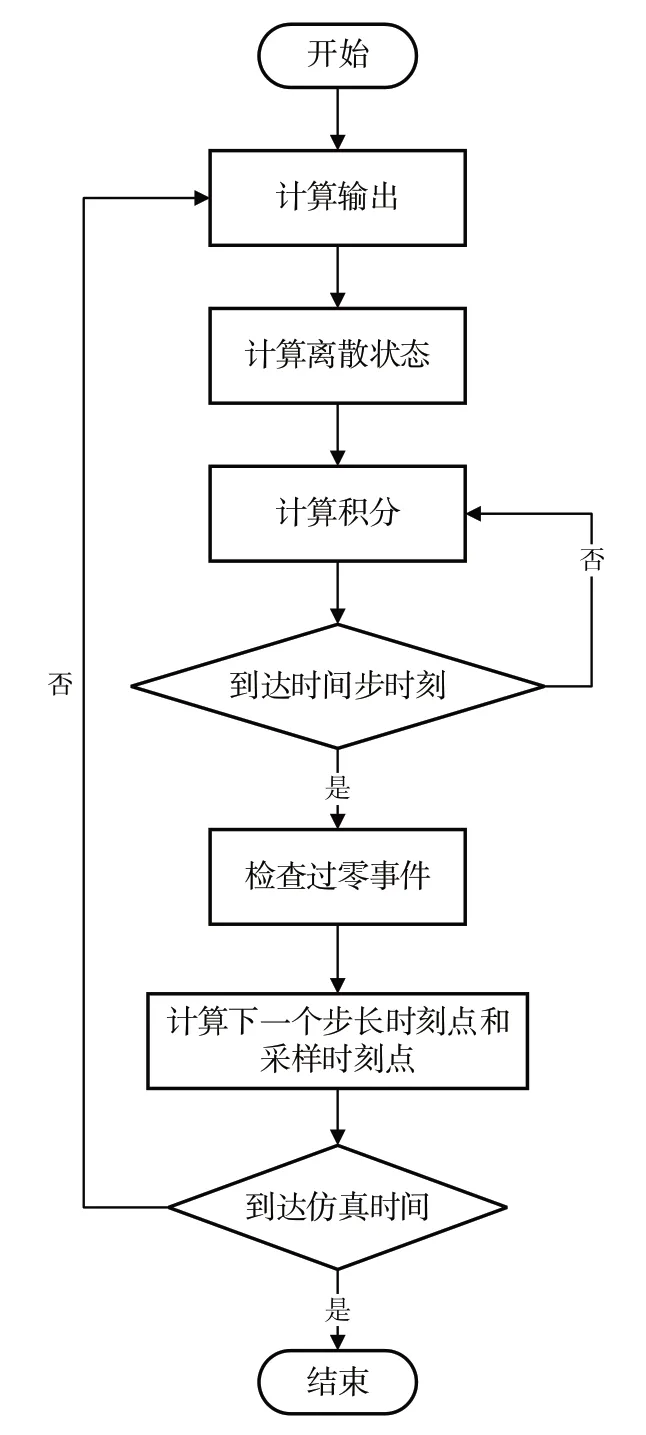
Fig.10 Flow of simulation calculation图10 仿真计算流程
仿真开始时,模型会设定系统的初始状态和输出,然后在每个时间步中计算系统输入、状态和输出的新值,并对模型进行更新(不涉及拓扑结构的更改)以应用这些计算结果。当仿真结束时,模型将输出用户所关心的模块状态及模块的最终值。
在仿真计算流程的一开始,执行引擎会调用计算输出模块的输出方法使仿真器开始工作,仿真器将根据模块状态更新顺序表指定的计算顺序依次调用模块的更新方法。对于基础模块的状态更新,如果模型中仅有离散状态模块,仿真器会根据采样时间计算仿真步长(可以是固定步长,也可以是可变步长),并调用模型的更新方法。模型会按顺序调用每个基础模块的更新方法。
对于包含连续状态的模型,仿真器将使用求解器对模型进行求解。具体地,根据求解器的数值积分算法,求解器会进入子时间步循环。在子时间步中,模块会以更小的仿真步长进行计算。在该循环中,求解器会重复调用模型的更新方法,使得在一个主时间步中可以按照连续时间间隔计算模型的输出。使用该方法可以提高数值积分计算的准确度。
最后,仿真器会判断是否到达仿真结束时间,如果没到,则循环上述过程;如果到达,则结束仿真并输出结果。
3.4 离散状态模块计算
离散模块的典型代表就是单位时延模块。单位时延模块在每个时间步的输出结果是上一步结果的值,在0 时刻的初值是一个指定值。以上定义是在采样时间与仿真步长相同的情况下,在实际情况中,采样时间与仿真步长可能不一致。仿真步长是指模型在仿真时运算的间隔时间,例如设置为0.1 的步长意味着每隔0.1 s,整个模型系统就要进行一次计算。而模块的采样时间是一个参数,其指示在仿真过程中模块何时生成输出,并在适当时更新其内部状态[20]。内部状态包括但不限于记录的连续状态和离散状态。模块的采样时间可以由用户指定,如果无需关注每个仿真步长的结果,通常可以将采样时间设置为仿真步长的整数倍。因此,修改后的时延模块定义如下:单位时延模块在每个采样时间的输出结果是上一个采样周期的值,在0 时刻的初值是一个指定值。例如,若仿真步长为0.1,采样时间为1,则在0~0.9 的仿真时间内,模块的输出均为x(0);在1.0~1.9 的仿真时间内,模块的输出为x(1),以此类推。
3.5 连续状态模块计算
连续状态系统通常采用微分方程的形式进行系统建模,因此连续状态模型的求解依赖于数学上的数值积分算法。连续状态求解并不是在真正的连续时间下进行计算,而是将时间分割成足够密集的时间点去模拟连续计算。
该软件实现了欧拉法和四阶龙格库塔法两种数值积分求解器,从而支持连续状态模型的求解。欧拉法的计算相对简单,此处不再赘述,本节将着重介绍四阶龙格库塔法。四阶龙格库塔法简称RK4 法,采用高阶的非因果数值积分求解方法能在保证高精度的同时,具有良好的通用性、稳定性和灵活性[21]。
四阶龙格库塔法采用离散化的时间步长来解决连续问题,在每个时间步内计算若干个点的函数斜率,并使用这些点斜率的平均值去估计下一个时间步的函数值。其大致流程如下:
(1)在每个时间步内,计算函数在当前仿真时间点的导数以求得斜率,并使用若干个仿真时间点与下一个时间点的中间点计算斜率,之后将上述斜率的加权平均值作为当前仿真步的斜率。
(2)使用上一步得到的斜率更新下一个时间步函数值。
使用数学公式描述上述流程如下:
微分方程的初值表示为:
则使用RK4对该方程的求解为:
其中:
其中,h 代表仿真步长。通过上述计算,函数在下一时刻的值由当前值与当前值附近若干点的斜率和仿真步长所决定。
根据上述数值积分算法可以得出,在每个仿真步长内,涉及到数值积分的计算仅发生在当前仿真时刻tn、tn+和tn+h 3 个时间点。因此,在涉及连续状态的模型求解时,需要将单个仿真步长的计算细化为3 个阶段,在此3 个阶段内完成离散状态的求解与更新以及连续状态下方程的数值积分求解。具体的,在tn和tn+h 两个仿真时刻都会触发离散模块的计算,而由于下一个仿真时刻tn+1=tn+h,因此在下一个仿真时刻会发生离散模块的重复计算。此类重复计算在存在特定模块(如计数器模块)时会影响结果。为避免这种情况的发生,需要在tn+h时刻设置离散模块的状态为未启用来阻止含有状态的离散模块更新。
三阶段的单步仿真流程如图11 所示。在每一个单次仿真时间步内,首先会按照模块更新顺序表更新除积分器外的其他基础模块。具体地,首先会针对时延模块调用更新输出值函数,使得时延模块的初始值或上一个时间步计算的状态值更新到输出。接着会调用所有时延模块和输出模块的更新函数,以计算时延模块当前时间步的值,并从所有输出模块出发,按照模块更新顺序表对应的顺序更新与输出相连的模块。在此过程中,可以计算RK4 中的k1。当其他全部模块的状态更新完成后,将禁用上文中提及的模块以避免产生重复更新错误,然后将时间步设置为,计算k2和k3。最后,将时间步设置为tn+h,计算k4和yn+1。计算完成后,启用刚才禁用的全部模块,并重复上述过程进行下一时间步的计算,直到仿真结束。
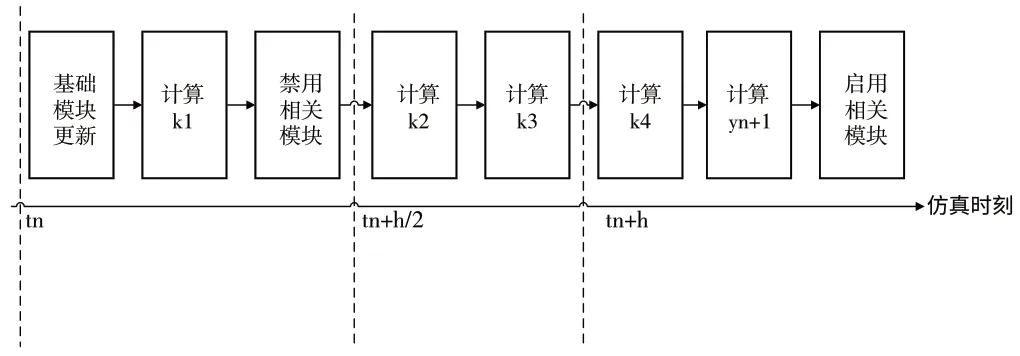
Fig.11 Three stages of single-step simulation图11 单步仿真3个阶段
通过上述过程即可实现离散和连续系统的混合仿真。当需要增添新的解算器时,需根据实际的数值积分算法进行阶段的微调,但总体计算顺序不变。
4 测试与验证
为了对仿真系统实例进行测试,本节根据基础模块框架分别搭建了3 种不同类型的基础模型实例,并在Simulink 中搭建同样的3 个模型,通过对比来验证基础模型仿真求解器仿真结果的可靠性与准确性。
4.1 离散系统仿真
本文以汽车制动系统中线性化的滑移率—附着系数关系模型作为离散系统仿真实例。防抱死制动系统(Antilock Brake System,ABS)的主要功能是通过控制车轮滑移率来动态调整车轮产生的最大摩擦力,进而保证车辆在制动过程中能够保持较为稳定的转向控制,并在最短距离内停车。车轮与地面之间的摩擦系数μ又称为路面附着系数,其与车轮滑移率s之间存在着一定的非线性关系。在此本文将其用两段直线进行近似处理,得到两段式的路面附着系数与车轮滑移率的变化关系。其变化规律可由公式(4)所示的分段差分方程表示,其中μh表示路面附着系数的峰值,μg表示车轮完全抱死时的路面附着系数,s0表示路面附着系数处于峰值时所对应的轮滑率:
车轮轮滑率的取值范围为0~1,为模拟路面附着系数随车轮轮滑率的线性变化,本文搭建了如图12 所示的模型。模型覆盖了常数模块(Constant)、单位延迟模块(Unit-Delay)、加法模块(Sum)、If 分支模块(IfBlock、IfAction)、信号合并模块(Merge)以及输出模块(Output)。其中,对于公式(4)所涉及的变量,设置μh=0.8,μg=0.6,s0=0.2。该模型的输入是常量0.001,代表一个时间步的步长。首先使用单位时延模块,延后一个时间步对变量u1进行0.001(即一个时间步)的累加,使u1代表当前时间步长。将变量u1输入给一个逻辑判断模块,如果u1的值小于或等于0.2,则进行公式(4)中第一行的计算,否则进行公式(4)中第二行的计算。二者的计算结果通过merge 模块复合在一起,并输出到显示模块,最终输出函数图像。

Fig.12 Relationship model between linearized slip rate and adhesion coefficient图12 线性化滑移率—附着系数关系模型
在使用本仿真求解器进行仿真运算时,设置仿真时长为1 s,仿真步长为0.001 s,求解得到如图13 所示的滑移率—附着系数关系曲线。同时在MATLAB(R2022a)/Simulink 中选择同样的仿真模型,设置步长类型为定步长,求解器为离散(无连续状态)类型,通过仿真运行得到如图14所示的滑移率—附着系数关系曲线。
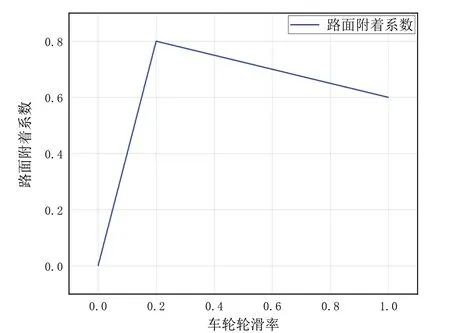
Fig.13 Curve depicting the relationship between slip rate and adhesion coefficient(simulation results of this software)图13 滑移率—附着系数关系曲线(本文软件仿真结果)
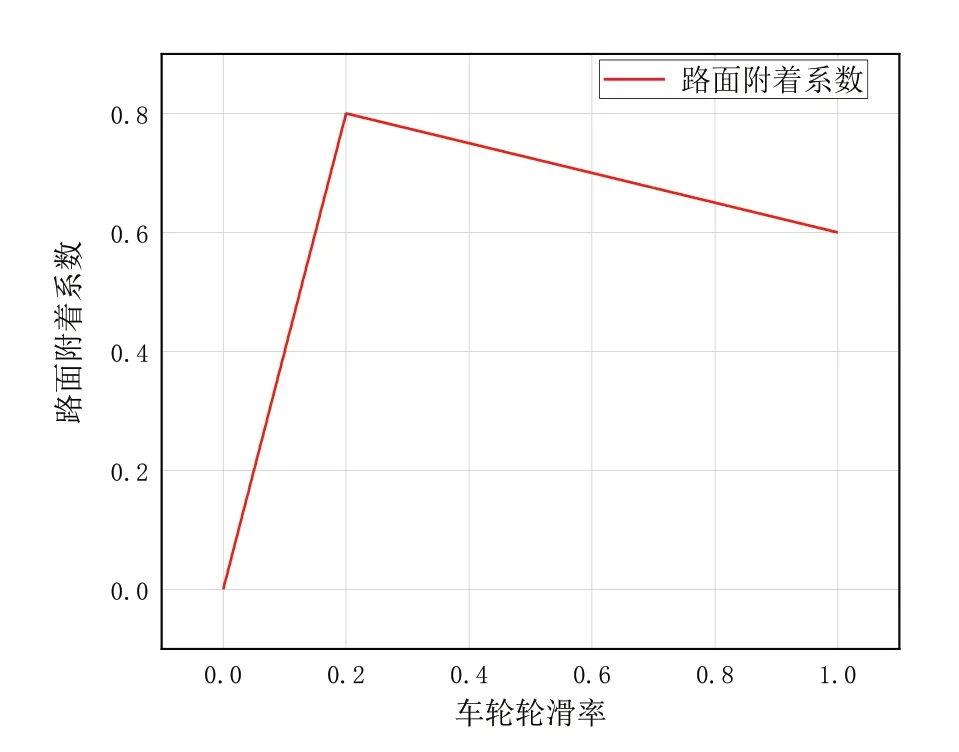
Fig.14 Curve depicting the relationship between slip rate and adhesion coefficient(simulation results of MATLAB(R2022a)/Simulink)图14 滑移率—附着系数关系曲线(MATLAB(R2022a)/Simulink仿真结果)
4.2 离散系统仿真
本文以弹球模型作为连续系统仿真的实例。弹球模型是一个经典的物理学问题,也是一个典型的基础连续系统模型。当一个球以一定的初速度和角度从一定高度自由落下时,其将受到重力的作用加速下落。当球碰到地面时,其能量将转换成弹性形变的势能,并随即释放出来,使球反弹起来。根据牛顿第二定律,球的速度变化和位置变化都是连续的,如公式(5)所示。其中,g表示重力产生的加速度,x(t)表示球在t时刻的位置,v(t)表示球在t时刻的速度。
当小球落到地面并与地面发生弹性碰撞时,其碰撞前后的速度变化可由公式(6)表示。其中,k是小球的恢复系数,v-是小球碰撞前的速度,v+是小球碰撞后的速度。
整个弹球系统模型如图15 所示,模型覆盖了常数模块(Constant)、增益模块(Gain)、积分模块(Integrator)、关系运算模块(RelationalOperator)以及输出模块(Output)。其中,对于公式(5)和公式(6)所涉及的变量,设置模型参数g=9.81,k=0.8,弹球初始速度v0=15,初始位置x0=10。该模型的输入是常量-9.81,代表重力系数,输出是速度积分器和位置积分器在每一个时间步的结果(即小球的速度和位置变化)。对于速度积分器,常量-9.81 作为积分参数输入,常量15 代表初速度,是积分器的初始值(仅在仿真开始时生效),-0.8 代表反弹速度转换系数,是小球每次落地后经过反弹得到的反向速度值(即若以v0的速度落地,则弹起的瞬时速度为-0.8v0)。对于位置积分器,常量10为小球的初始位置值,也作为位置积分器的初值(仅在仿真开始时生效)。将速度积分器的结果作为距离积分器的输入进行积分计算,得到小球在该步长时间内的距离值。此外,两个积分器会对距离是否大于或等于0 进行判断。当距离结果由小于零转换到大于或等于零时,会触发速度积分器和距离积分器的上升沿信号进行重置运算,将距离结果重置为0,速度结果重置为当前结果乘以-0.8。
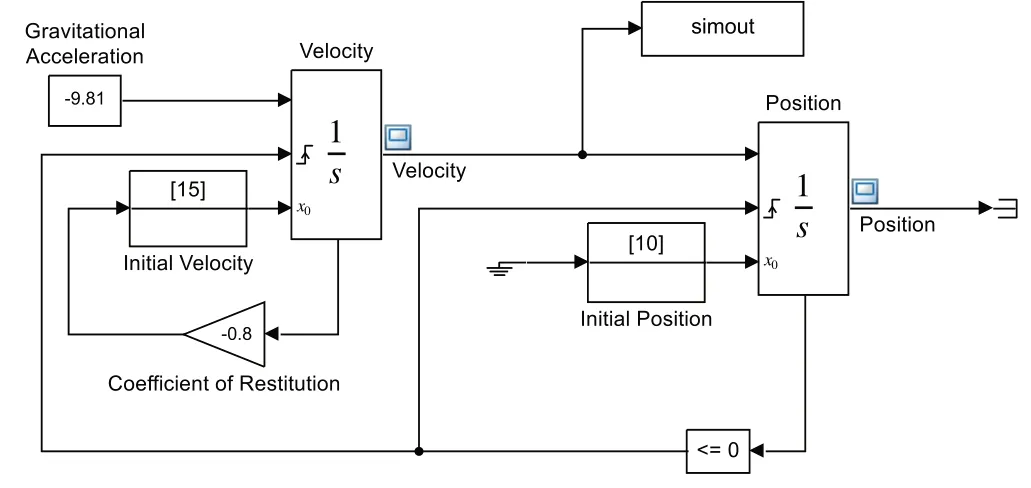
Fig.15 Model of bouncing ball system图15 弹球系统模型
在使用本仿真求解器进行仿真运算时,设置参数如下:设置仿真时长为20s,仿真步长为0.01s,得到如图16 所示的有关小球速度和位置变化的仿真曲线。同时在MATLAB(R2022a)/Simulink 中选择同样的仿真模型,设置步长类型为定步长,求解器类型为ode4(Runge-Kutta),通过仿真运行得到如图17 所示的关于小球速度和位置变化的仿真曲线。
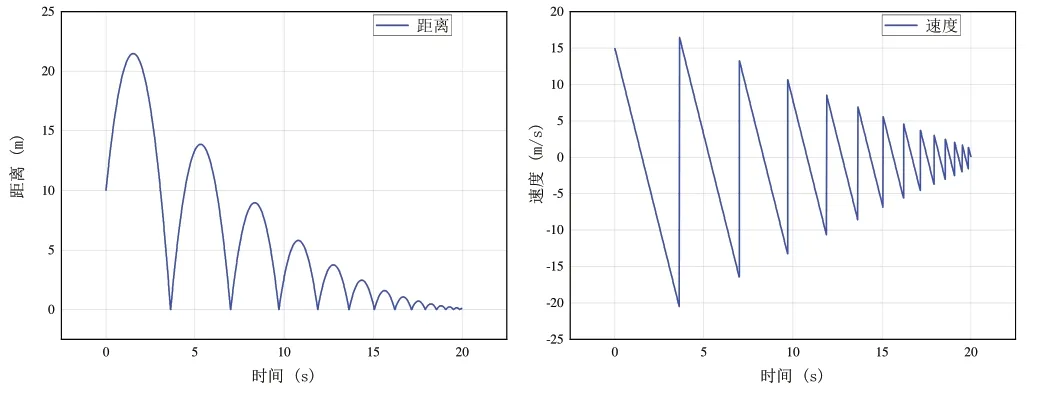
Fig.16 Velocity and position change curve(simulation results of this software)图16 速度与位置变化曲线(本文软件仿真结果)
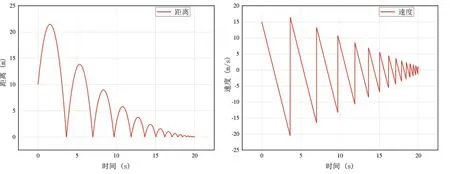
Fig.17 Velocity and position change curve(simulation results of MATLAB(R2022a)/Simulink)图17 速度与位置变化曲线(MATLAB(R2022a)/Simulink仿真结果)
4.3 混合系统仿真
混合系统中既包含连续状态的求解,又包含离散状态的求解,在实际仿真中应用广泛。例如在控制系统中,控制器的状态通常是离散的,而被控制的系统状态是连续的,因此需要使用混合系统模型来描述整个控制系统。另外,混合系统模型也被广泛应用于嵌入式系统中,例如汽车电控单元、飞机控制系统等。
本文以汽车行驶速度控制系统作为混合系统的仿真实例,如图18 所示。汽车行驶控制系统控制着汽车在行驶过程中的速度变化,其工作原理是先测量汽车的实际速度,然后根据汽车速度操纵机构的位置计算汽车的理论速度。通过这两个速度的差值计算应该施加的牵引力,并由此牵引力改变汽车速度,直到其稳定在指定的速度为止。其中,对实际速度的计算是连续的,其余的数值计算是离散的。
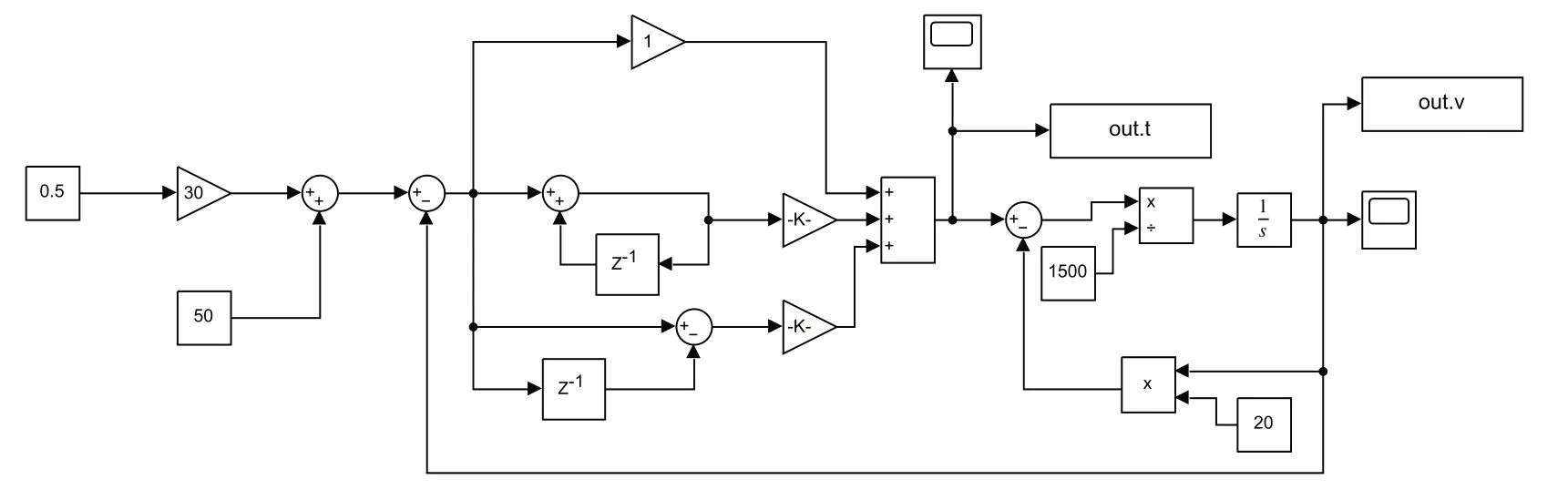
Fig.18 Model of automobile speed control system图18 汽车行驶速度控制系统模型
对于汽车理论速度的计算,其数学模型可由公式(7)表示。其中,x表示当前时刻汽车速度操纵机构的位置,vstandard表示根据汽车速度操纵机构位置计算出的汽车的理论速度。
对于汽车实际速度的计算,其数学模型可由公式(8)表示。其中,F表示汽车牵引力,m表示汽车质量,b表示摩擦阻力因子,vreal表示汽车的实际速度。
汽车牵引力则由行驶控制器PID 根据汽车当前速度与指定速度的差值计算得到,其数学模型可由公式(9)表示。其中,u(n)表示系统输入的理论速度,y(n)表示系统输出的牵引力;s(n)为一个中间量,表示对速度进行时延累加;KP、KI、KD分别为PID 控制器的比例、积分与微分控制参数。
汽车行驶速度控制系统模型如图18 所示,模型覆盖了常数模块(Constant)、增益模块(Gain)、加法模块(Sum)、减法模块(Subtract)、单位延迟模块(UnitDelay)、乘法模块(Product)、除法模块(Divide)以及输出模块(Output)。其中,对于公式(7)—公式(9)所涉及的变量,本文设置模型参数KP=1,KI=0.01,KD=0.01,m=1500,b=20,并设置延时模块采样时间为0.02s。在该模型中,输入为操纵机构的位置,用常数0.5 表示,输出是汽车的实际速度和牵引力。首先根据公式(7)计算出汽车的理论速度作为公式(9)中的u(n)输入系统,此时模型的计算分为3 路:最上路将u(n)直接输出,对应公式(9)中的KPu(n);中路将u(n)与一个单位时延前的结果相加,即s(t)=s(t-1)+u(t);下路将u(n)与一个单位时延前的结果相减,即d(n)=u(n)-u(n-1)。以上3 路结果按公式(9)中的牵引力输出公式进行计算,得到当前时刻的牵引力。该牵引力参与公式(8)的积分计算,得到实际速度。
在使用本仿真求解器进行仿真运算时,设置参数如下:仿真时长为1 000 s,仿真步长为0.01 s,求解得到如图19 所示的汽车牵引力与行驶速度变化曲线。同时,在MATLAB(R2022a)/Simulink 中建立同样的仿真模型,设置步长类型为定步长,求解器类型为ode4(Runge-Kutta),仿真运行得到如图20 所示的汽车牵引力与行驶速度变化曲线。
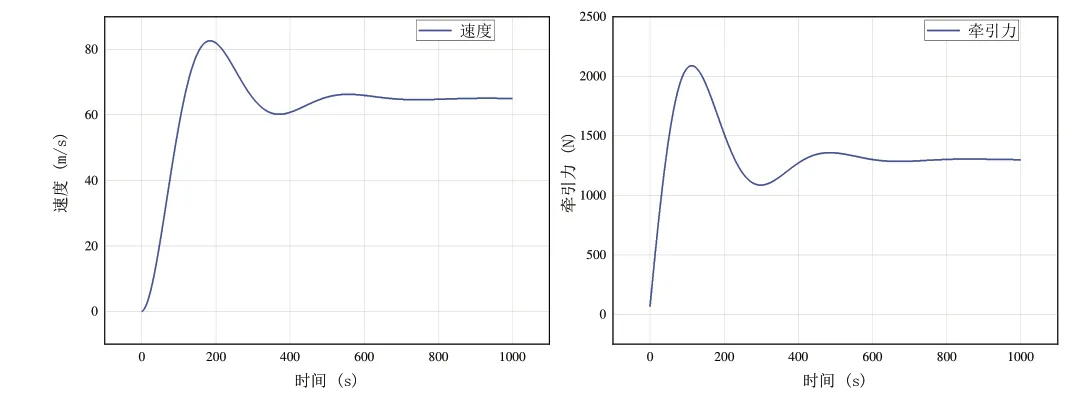
Fig.19 Curve depicting the relationship between automobile traction force and velocity change(simulation results of this software)图19 汽车牵引力与速度变化曲线(本文软件仿真结果)
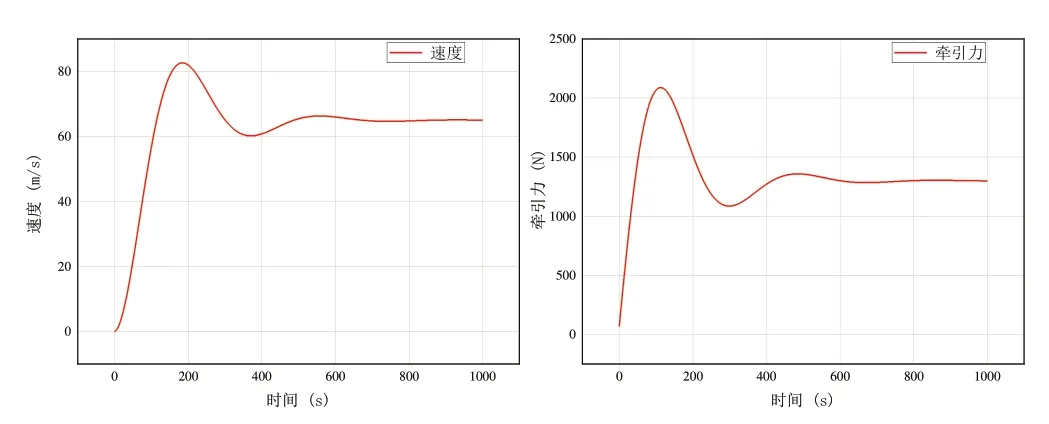
Fig.20 Curve depicting the relationship between automobile traction force and velocity change(simulation results of MATLAB(R2022a)/Simulink)图20 汽车牵引力与速度变化曲线(MATLAB(R2022a)/Simulink仿真结果)
5 结语
本文主要围绕如何从零开始搭建一个领域系统仿真软件的问题,从仿真软件的相关基础理论开始,阐述了基于CBD 的仿真系统的仿真计算流程,并介绍了相应算法。在软件实现上,从软件整体架构出发,介绍了如何搭建仿真基础模块库,并阐明了如何设计一套仿真流程以支持离散事件系统仿真和连续事件系统仿真两大仿真功能。对于微分方程的求解,采用业界常用的四阶龙格库塔法,并提出在仿真流程中使用四阶龙格库塔法进行微分方程求解的方法。最后针对多个领域的仿真典型案例,使用本文设计的软件与常用仿真软件MATLAB(R2022a)/Simulink进行了对比测试,本文设计的软件在准确度和效率上符合预期。
本文仿真方法的优点在于采用了接口式设计,代码各个模块之间的耦合度较低,可以按照接口规范快速实现对基础模块库和解算器的扩充,以提升模型的仿真能力。本文方法的局限性在于:对模型的仿真范围在很大程度上依赖于基础模块库,基础模块库限制着模型的表达能力,而没有提供一套可编程的形式供用户自己编程实现相应基础模块的计算逻辑。

