水下平板流激声辐射快速预报方法研究

胡昊灏, 周石头, 赵 傲, 蒋哲伦

(江苏科技大学 船舶与海洋工程学院,江苏 镇江 212000)

水下航行器中高航速行驶时,会在结构表面产生湍流脉动压力,并引起流激振动噪声[1]。准确预报航行体流激噪声,对水下结构减振降噪和声隐身有重要意义[2-3]。由于这类噪声涉及到流场、结构、声场等多重因素,且具有典型时空随机性,所以研究起来存在难度。

Graham[4]通过模态展开法建立了流激平板声辐射的解析理论,为掌握流激噪声产生规律奠定了理论基础。当水下结构形状复杂时,解析公式不再适用,Chevalier等[5]总结了水下航行器流激自噪声和辐射噪声的工程数值预报方法,小尺度模型一般先采用计算流体动力学 (computational fluid dynamics,CFD)大涡模拟计算结构表面湍流脉动压力,然后导入声振有限元模块计算流激声辐射,而对于大尺度模型CFD计算效率无法满足工程要求,一般用半经验公式描述湍流脉动压力,吕世金等[6]通过风洞测量获取了回转体表面的湍流脉动压力,发现测试结果与Corcos模型经验公式有较好的一致性。Maxit等[7]比较了采用空间-频率谱和波数-频率谱两种形式的湍流脉动压力经验公式数值求解流激噪声的计算效率,指出空间-频率谱有限元法由于要构造大维数激励力矩阵,对内存占用严重(即使采用矩阵分解法依然如此),从而导致计算效率低,而波数-频率谱则能明显降低内存占用,同时物理意义更清晰,然而关于波数-频率谱形式的有限元法研究目前还很少。

Aucejo等[8]提出了一种用于替代风洞中测量流激振动的试验方案,该方法用若干组空间随机分布的非相关平面波叠加来替代湍流脉动压力波数-频率谱。本文在此基础上,提出一种基于非相关平面波叠加的方法合成湍流脉动压力,并结合有限元模块建立波数-频率域的流激噪声数值预报方法,探索了相关参数对计算精度的影响。

1 平板流激声辐射基本理论

如图1所示,长为Lx,宽为Ly的矩形平板四边简支在无限大刚性障板上,在充分发展的湍流作用下,计算上半空间无限大声场的流激辐射噪声,这里假设弹性板的振动不会对流场产生影响。

图1 流激平板声辐射示意图

此时弹性板的运动方程为

D∇4w(x,y)-ρshω2w(x,y)=-pt(x,y)+pa(x,y)

(1)

式中:w为板法向位移;ρt为作用在板表面的湍流脉动压力;pa为板表面声压负载。通过解析法可以求得弹性板振速谱Svv(x,ω)和辐射声功率谱Πrad(ω)

(2)

Πrad(ω)=

(3)

式中:ΦPP(k,ω)为湍流脉动压力波数-频率谱;Hp(x,k,ω),Hp(x,k,ω)分别为振动传递函数以及声压传递函数,其物理意义为在波数为k单位平面波激励下,x位置处的振速或声压响应。

2 非相关平面波流激声辐射有限元法

2.1 非相关平面波叠加等效法

用非相关平面波叠加来合成湍流脉动压力,是指通过一组空间随机分布的广义平面波叠加来等效湍流脉动压力激励力,该技术的关键是获得平面波的等效幅值,具体的理论如下:

假设每一组平面波(这里指的广义平面波)的表达式为

Pxy(x,y,t)=Axy(t)ejkxx+jkyy

(4)

式中:Axy(t)为平面波幅值;kx,ky分别为x,y方向的波数。

对空间任意两点处的平面波作统计相关运算然后作傅里叶变换,得到空间-频率谱函数表达式为

SPxyPxy(ξx,ξy,ω)=SAxyAxy(ω)ejkxξx+jkyξy

(5)

式中:ξx,ξy分别为空间两点沿x轴和y轴的空间距离;SAxyAxy(ω)为平面波的自谱。

当多组形如(4)式的平面波叠加作用时,空间某点(x,y)处的压力之和为

(6)

由于假设了各组平面波之间非相关,那么满足当x≠x′,y≠y′时

SAxyAx′y′(ω)=0

(7)

相应的总压力空间-频率谱密度函数为

(8)

式(4)～式(8)给出了多组平面波叠加后的总压力空间-频率谱,下面要将这种谱与湍流脉动压力波数-频率谱建立联系。

由空间傅里叶变换关系可知,湍流脉动压力的空间-频率谱与波数-频率谱满足如下关系

SPP(ξx,ξy,ω)=

(9)

式中,ΦPP(kx,ky,ω)可由脉动压力的波数-频率谱经验公式给出。对式(9)的积分进行波数域离散得到

SPP(ξx,ξy,ω)=

(10)

对比式(8)和式(10)可知,当自谱SArsArs(ω)满足式(11)时,湍流脉动压力波数-频率谱可由多组非相关平面波叠加来等效

(11)

2.2 流激声辐射有限元法流程

由2.1节分析可知合成的湍流脉动压力表达式为

(12)

式中,φij为均匀分布在[0,2π]上的空间随机相位,表示平面波是空间非相关的。

(13)

(14)

式中,α1=0.116,α3=0.7分别为沿流向和展向的衰减系数。

表达式(12)将湍流脉动压力随机激励转化为一种确定性激励,此时可以通过常规有限元声振耦合技术来计算流激振动声辐射,对应的有限元方程为

(15)

式中:ul为结构位移;pl为辐射声压;K,H,M分别为刚度矩阵、耦合矩阵和质量矩阵;下标s和f分别为结构和流体。

本文对式(15)的求解过程是在商业有限元软件Comsol平台实现的,得到ul和pl后,结构的流激振动自谱以及辐射声功率谱分别为

Svv=-ω2E(uu*)

(16)

(17)

式中,E为数学期望。

计算流程如图2所示,首先利用式(12)得到等效平面波的幅值,将多组空间随机分布的平面波通过接口加载到Comsol平台建立声振耦合模型,将各组平面波激励下的响应进行平均即可得到流激振动与声辐射。

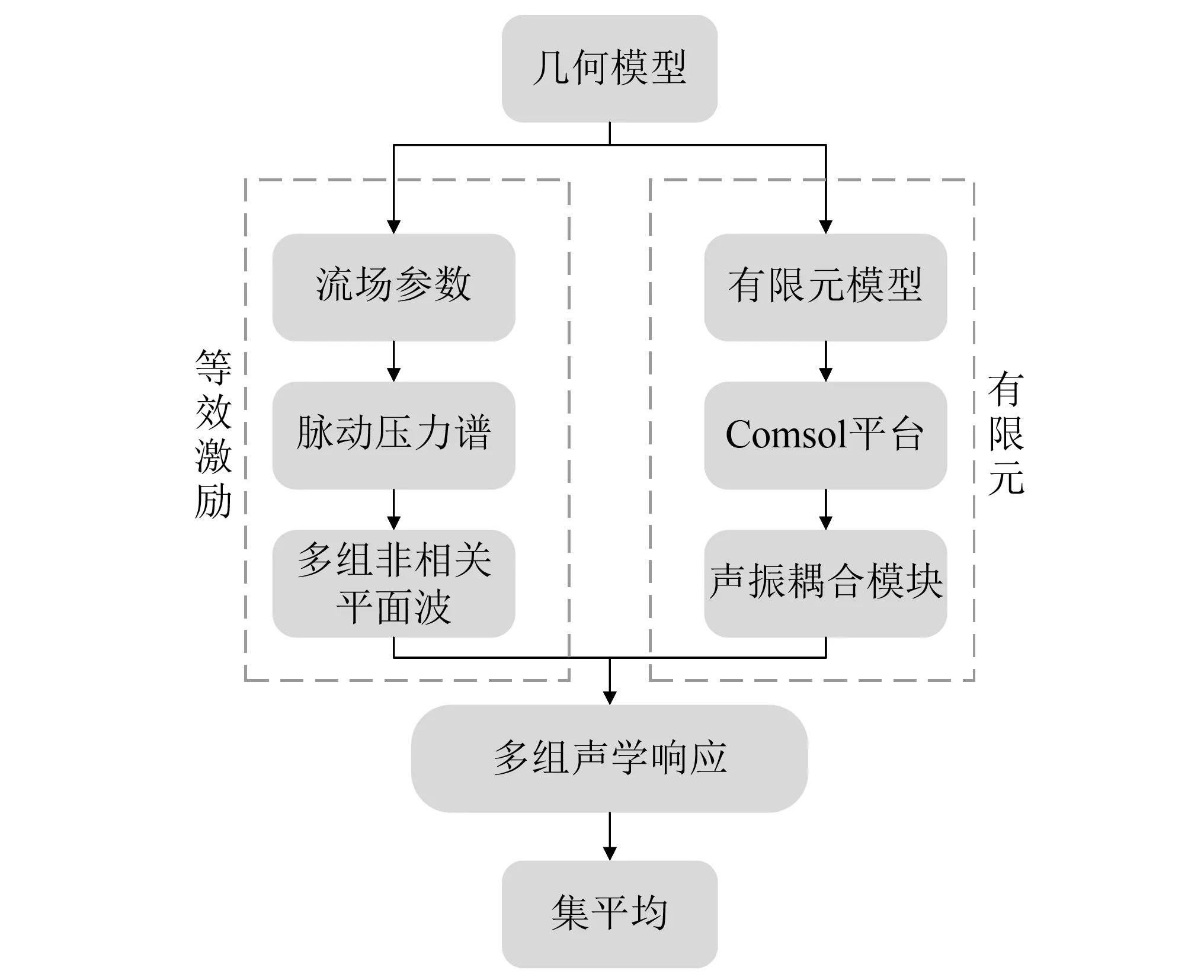
图2 计算流程图

3 算法验证

由前边理论可知,湍流脉动压力是由多组随机平面波(见式(12))所合成,因此最终的流激振动声辐射响应由各组平面波激励下的响应取平均值得到,图3展示了各组平面波激励下的响应曲线,图中黑色实线为各组响应的均值,后续计算分析中均采用此法。

例如，在学习《多位数乘一位数》这部分内容的时候，我为了让学生能够熟练地口算各种算式，我把学生分成了男女两队，让学生进行抢答对抗竞赛，男女两队在活动中，表现得特别踊跃，比赛状况十分胶着，两队都铆足了劲儿，要比出个上下来，通过组织这样的对抗竞赛，活跃了学生的思维的同时，学生为了取得好成绩，都积极地开动脑筋抢答问题，而且在竞赛中学生之间互相合作、团结互助，促进了学生之间的友谊，我对学生在竞赛中的良好表现做出了表扬，学生学习的劲头更足了，这样一来，这次的趣味性教学获得了圆满成功。

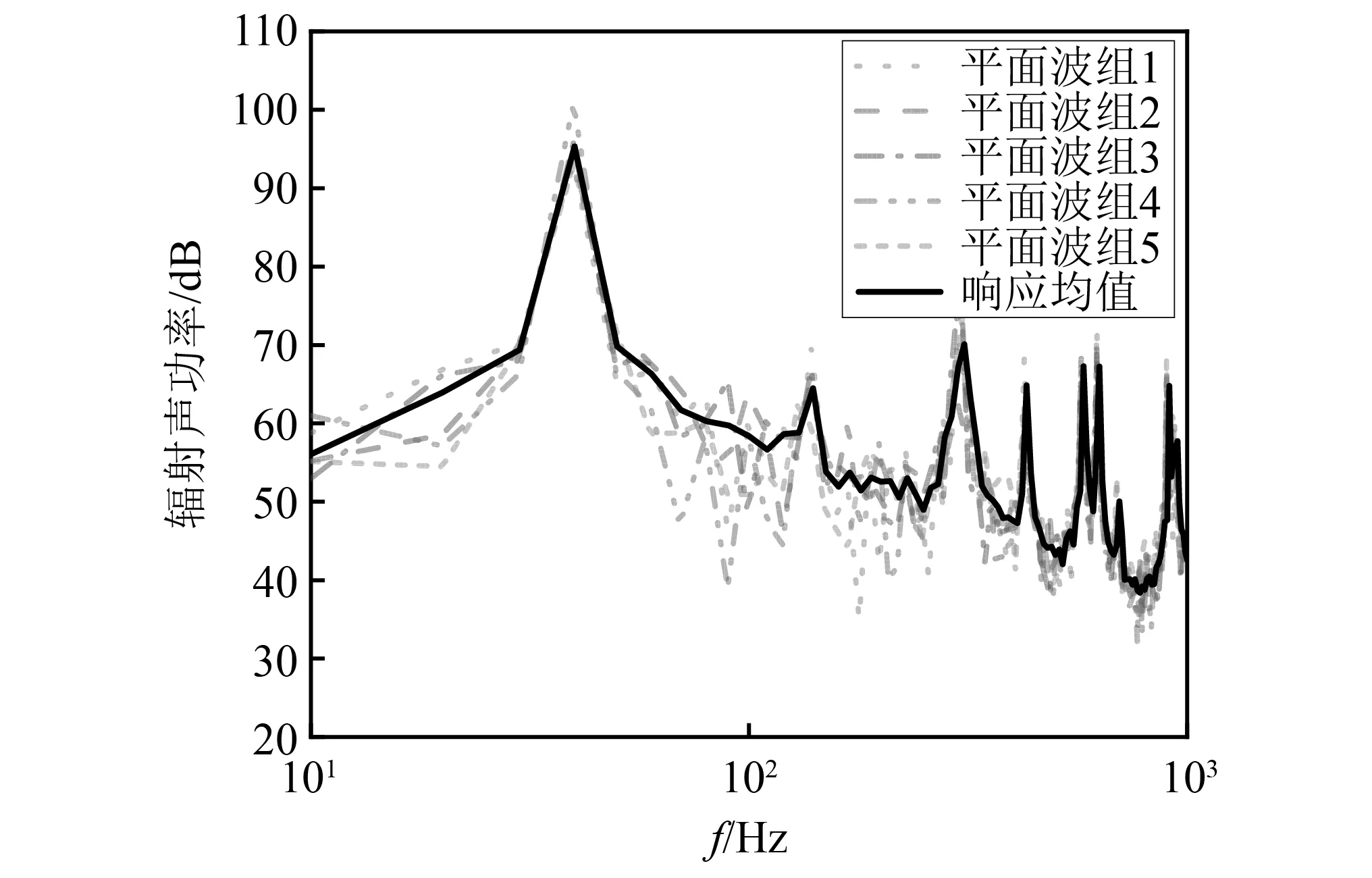
图3 多组激励下的平均响应

为了验证第2节中算法的正确性,在有限元软件Comsol中建立如图4所示的四边简支平板的有限元声振耦合模块,将多组等效平面波激励分别加载到弹性板表面,利用图3中的处理方法得到最终的平均响应。将有限元数值计算结果与流激平板解析值进行对比,来验证本文算法的正确性。

图4 有限元模型示意图

弹性板尺寸为Lx=Ly=0.5 m,厚度h=5 mm,材料为钢板,来流速度为U∞=5 m/s,后续计算分析均用此组参数。从图5可看出,本文算法与解析算法有较好的一致性,说明湍流脉动压力平面波等效合成方法结合有限元计算能够准确的预报流激声辐射。图中低频时两者有一定的误差,可能是因为解析解假设了无限大刚性障,而有限元法只能取有限尺寸的障板。

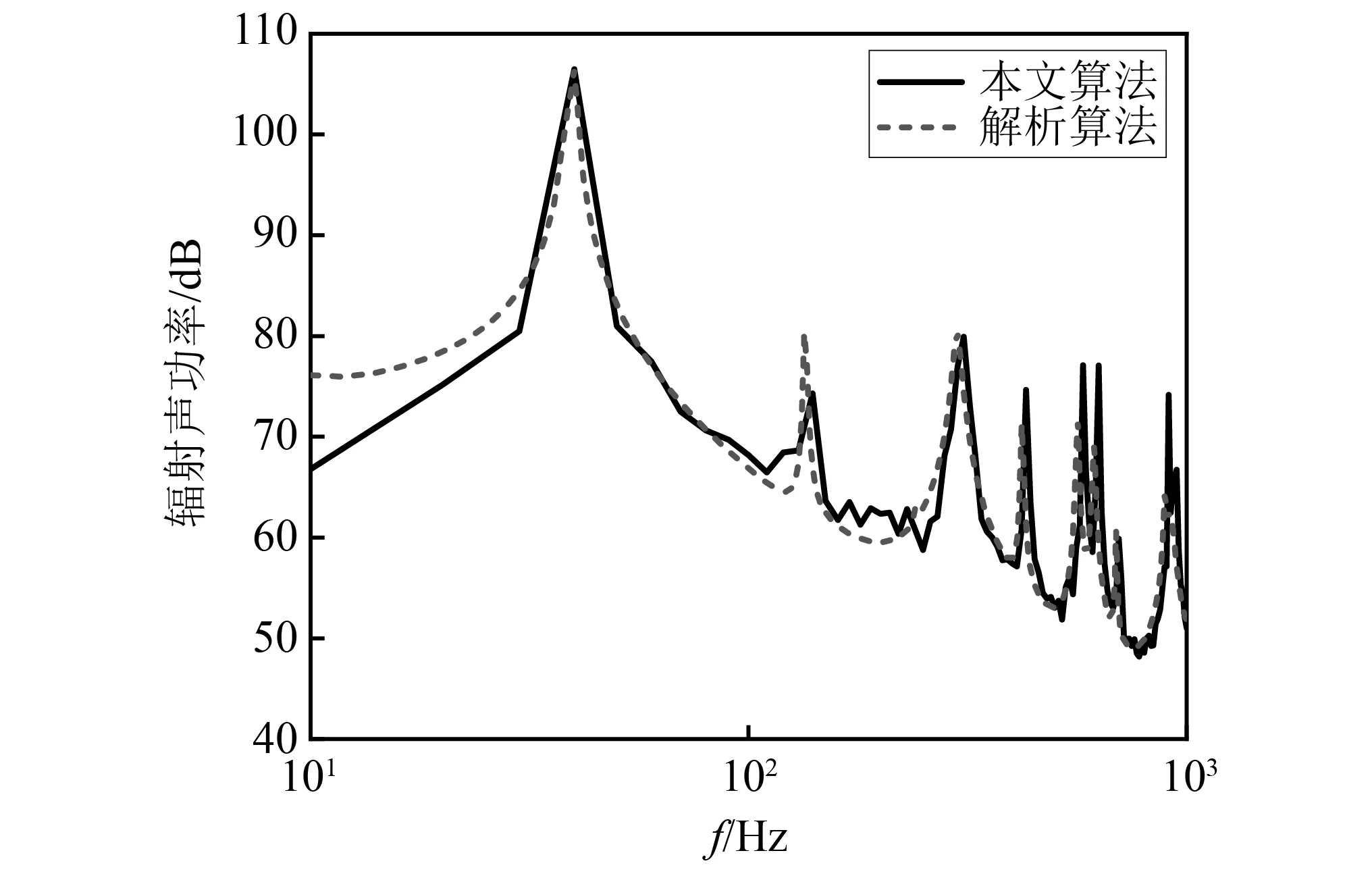
图5 算法验证

4 参数分析

由合成的湍流脉动压力表达式(12)可知,影响流激振动声辐射精度的因素包括截断波数范围、波数分辨率、平面波组数,另外有限元网格的划分准则也会影响计算精度,本节就这些问题展开讨论。

4.1 截断波数选取原则

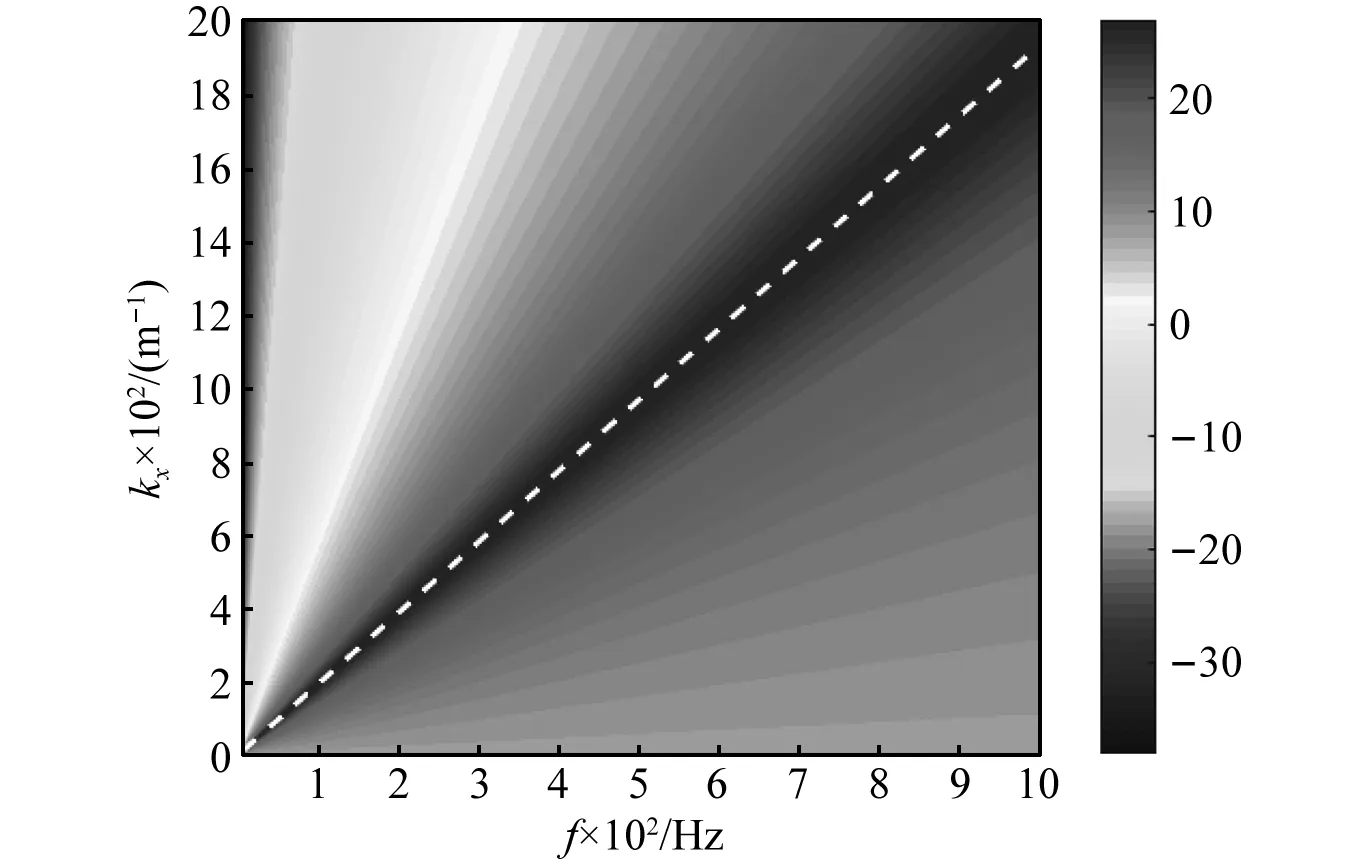
图6 湍流脉动压力波数频率谱

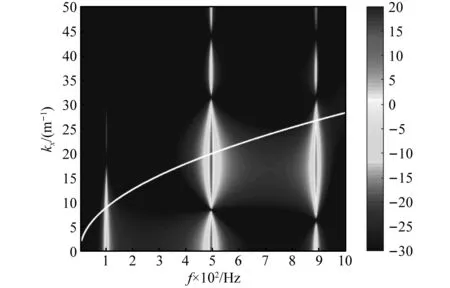
图7 平板振动传递函数波数频率谱

从图6可看出,湍流脉动压力最大值分布在迁移波数附近(白色虚线)。从图7可看出,平板振动传递函数响应最大值主要分布在小于等于弯曲波数的范围内。从图8可看出,流激振动响应的最大值也分布在弯曲波数附近。事实上只有当流速非常高时,流体迁移波数才能与结构弯曲波数耦合。因此这里初步将截断波数上限取定为结构弯曲波数。

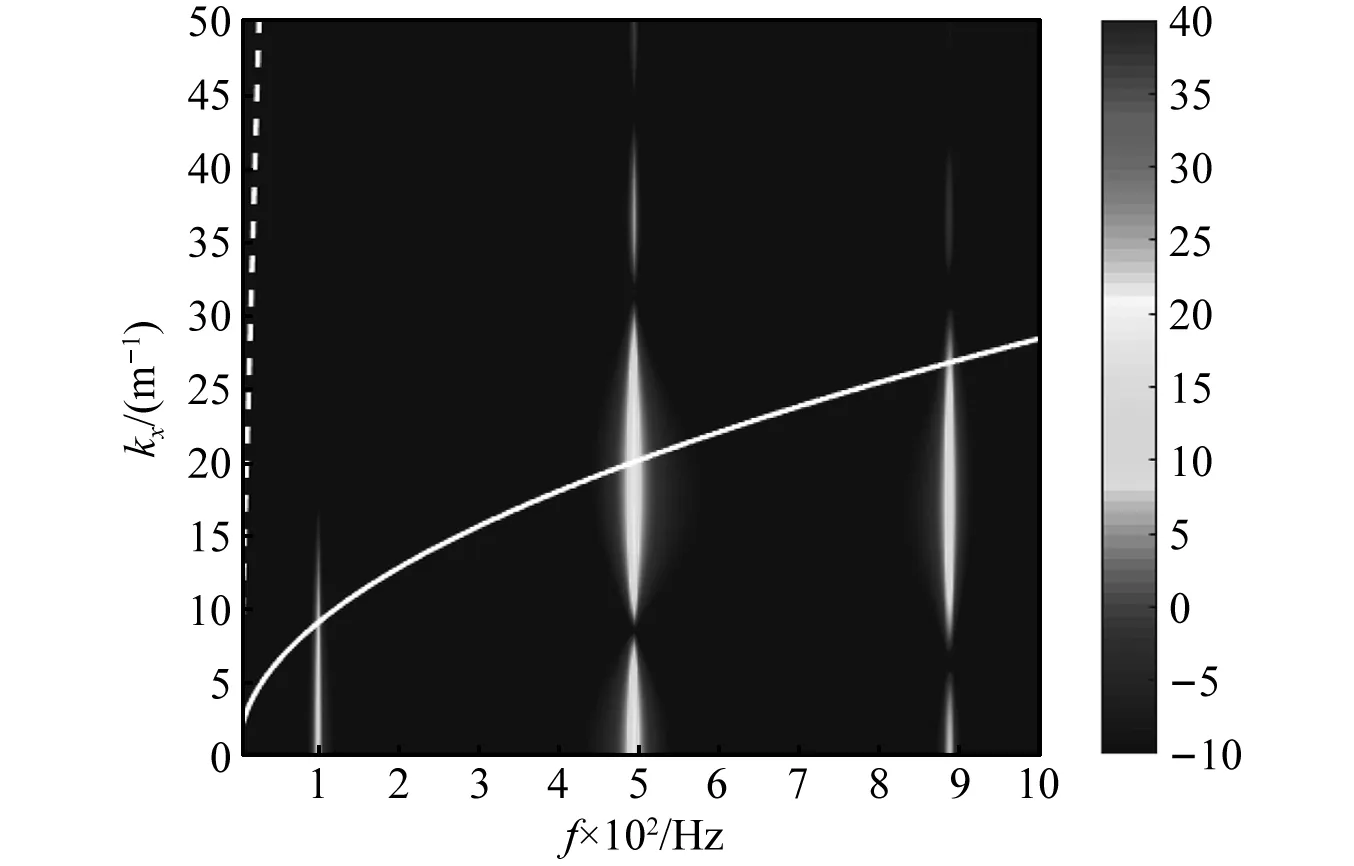
图与乘积波数频率谱

为了精细确认截断波数对流激声辐射的影响,图9给出了0.5kf和1kf,2kf(kf为弯曲波数)四种截断波数下的辐射声功率曲线,可以看出截断波数取两倍弯曲波数Kcutoff时,计算结果收敛。图10给出了1 000 Hz时两种截断波数下(0.5kf与4kf)板表面湍流脉动压力分布,4kf时的脉动压力场更精细。

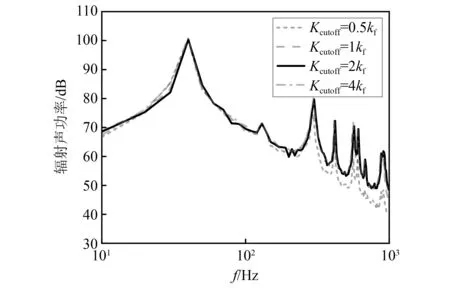
图9 截断波数的影响

图10 不同截断波数对湍流脉动压力场的影响

4.2 波数分辨率的影响

由式(12)可知,波数分辨率取值会影响湍流脉动压力谱的精度,原则上分辨率越高(对应波数分辨率数值越小)计算结果越准确。图11给出了几种不同波数分辨率取值对流激声辐射的影响,可以看出,波数分辨率对低频声辐射影响不大,对高频声辐射有一定的影响。综合考虑计算量和计算精度,这里取波数分辨率为。

图11 波数分辨率的影响

4.3 平面波组数的影响

在合成湍流脉动压力场时,理论上需要无穷多组形如式(12)的平面波叠加,然而在实际仿真时只能取有限组数,图12给出了不同组数非相关平面波叠加后的平板流激声辐射对比,可以看出随着平面波组数的增加,计算结果趋于收敛,平面波取10组与取20组的计算结果基本一致,综合考虑计算量的因素,这里取10组非相关平面波来合成湍流脉动压力场。

图12 平面波组数的影响

4.4 网格密度的影响

在采用有限元法计算声振耦合问题时,网格密度是影响计算精度的关键因素,尤其对于流激声振耦合问题的网格密度,不仅要考虑弹性结构、声场因素,还要考虑湍流脉动压力的空间分布,文献[9]指出,要获得收敛的流激振动声辐射结果,网格划分密度要远超常规的一个波长6个节点的准则,因此计算时间成本很大,无法用于分析一般工程问题。

另一方面,由于流激振动声辐射是随机问题,所以湍流脉动压力激励要考虑空间各点的互谱,从而导致激励力矩阵维度很大(需要进行Choslesky矩阵分解),进一步影响了计算效率。而本文提出的方法,则是将随机声振耦合问题转化为一般的确定性问题,降低了激励力矩阵维度,能有效提高计算效率。

图13比较了传统Choslesky分解法与本文算法的计算结果,可以看出采用同样的网格密度,本文算法与解析解有较好的一致性,而采用Choslesky分解法在中高频有较大的误差。要指出的是本文算法网格取0.5 mm时对应于一个波长4个节点的划分原则,即网格取π/2kf时,计算结果足够收敛。表1给出了不同算法单频的计算时间,进一步表明了本文算法的计算优势(所使用计算机内存为32 GB,CPU为酷睿i7 9700)。

表1 不同工况求解时间对比

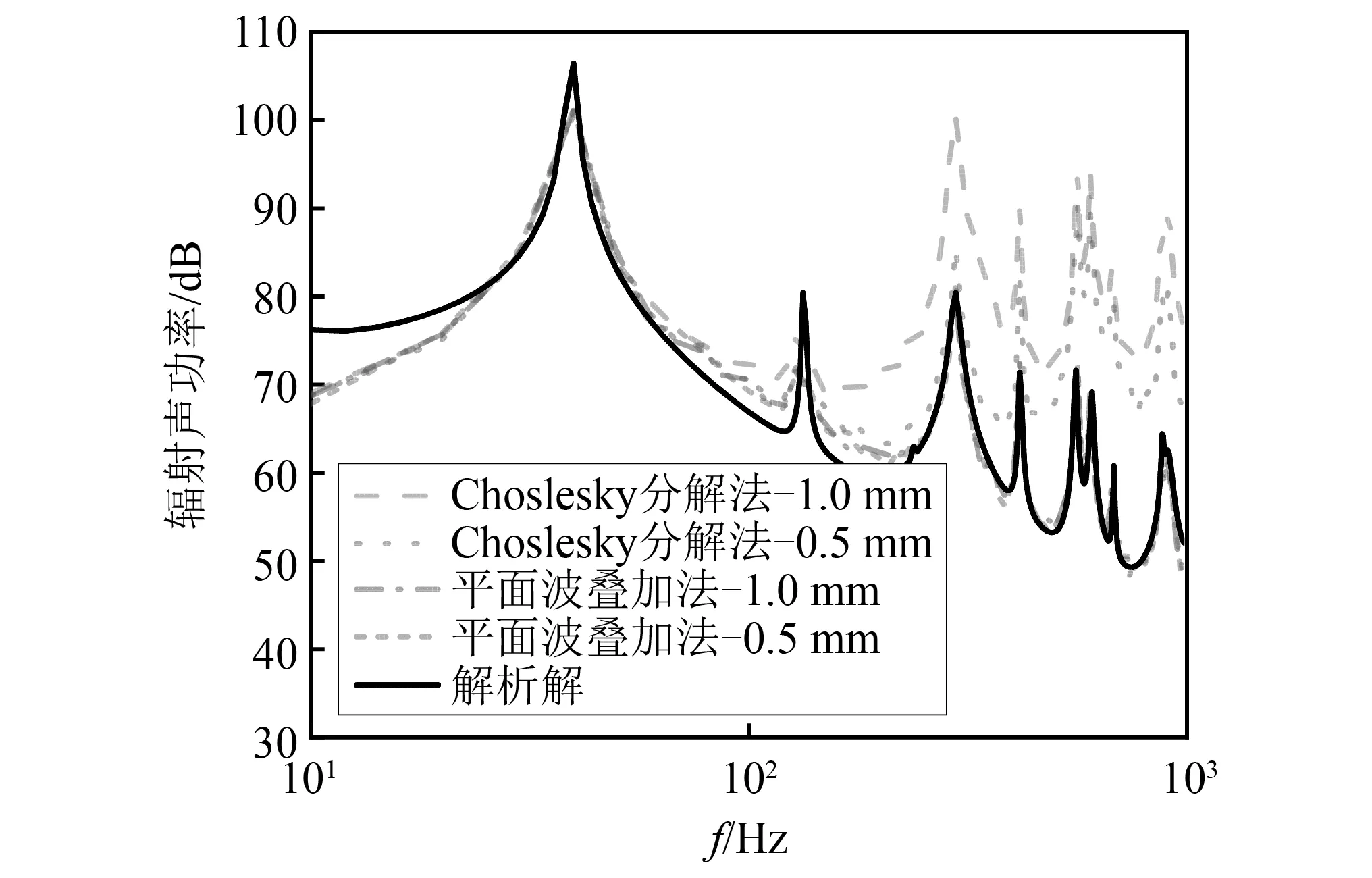
图13 网格密度的影响

5 结 论

本文以非相关平面波叠加技术为基础获得等效湍流脉动压力激励,并结合有限元声振耦合模块计算结构流激噪声,将随机声学问题转化为确定性问题。在深入分析流激噪声产生机理的基础上给出了影响该方法精度的准则,并得到如下结论:

(1)本文提出的数值预报方法能够准确预报结构流激振动噪声,并能显著提高计算效率。

(2)截断波数范围、波数分辨率、平面波组数等参数是影响湍流脉动压力激励力准确性的关键因素,需要根据文中的准则进行合理设。

(3)采用非相关平面波叠加法计算流激噪声时,声振耦合模型有限元网格密度要比传统方法稀疏,从而减少了计算负担。

为了使物理意义清晰明了,本文在进行流程描述和参数分析时均以矩形平板为例,后续研究将探索采用非相关平面波叠加法计算任意复杂结构的流激噪声。