结合微聚类和主动学习的流分类方法

尹春勇，陈双双

南京信息工程大学 计算机学院、网络空间安全学院，南京 210044

随着信息技术的飞速发展，数据的增长速度逐渐加快。来自生活中各领域的数据每时每刻都在以流的形式产生，例如社交平台的多媒体数据流、金融行业的交易数据流、交通领域的监控视频数据流。对这些数据流的挖掘和分析能够为进一步的管理提供重要的决策支持。与传统静态数据不同，数据流被定义为是高速连续的、无限的、动态变化的数据序列[1-2]，因此需要特殊的处理和挖掘算法。其中，数据流分类是数据流挖掘领域中一项关键技术。

数据流分类通常面临着概念漂移[3-4]的问题，即数据的潜在分布会随着时间的推移而发生不可预知的变化，而产生这种变化的原因有很多，例如季节的更替、温湿度的改变、设备线材的损耗。概念漂移问题会导致已有的分类模型无法适应新的数据分布，从而造成分类准确率的骤降。为了解决概念漂移问题，专家学者提出了一系列的解决办法。Ditzler 等[5]总结了两类解决方法，主动检测方法和被动适应方法。Brzezinski 等[6]利用最新到达的数据块创建基分类器，将其添加到集成中，通过更新基分类器权值应对渐变漂移。这种方法未考虑到数据块内发生概念漂移的情况，因此难以应对突变漂移，而且数据块的大小会影响分类性能，数据块过大，块中可能包含多个概念，导致对漂移的适应能力较弱；数据块过小，会由于块中样本不足导致无法很好地拟合数据分布，影响分类器的准确率。徐清妍等[7]利用滑动窗口检测概念漂移，窗口大小会影响概念漂移的检测，窗口过小容易受到噪声影响，造成误报；窗口过大会增加检测时间，且容易造成漏报[8]。

大多数应对概念漂移的分类方法处理的都是数据被完全标记的情况，在真实场景中，很多样本是无标记的，获取所有样本的真实标签既费时又费资源。针对这个问题，基于聚类的半监督方法[9-12]被提出。Masud等[10]提出了基于聚类的半监督分类器集成方法，首先数据流被划分为多个固定大小的块，每个部分标记的数据块利用聚类方法划分为多个簇，在新的数据块中训练分类器替换集成中性能最差的分类器，再使用标签传播算法标记未标记的聚类。Li 等[13]提出了一种基于优先标签数据流的半监督学习算法。该方法选择决策树作为分类器，在构造决策树的过程中，采用基于k-means 的聚类算法生成概念簇并标记无标签数据。通过比较之前和当前的概念簇判断是否发生概念漂移。Din等[14]提出了一种在线半监督学习方法（ORSL）。该方法利用在线微聚类实现对流数据的汇总，利用K最近邻（K-nearest neighbor，KNN）分类器预测传入的新实例：为每个分类器分配一个权重，选择权重最大的分类器作为最佳分类器，实现对新实例的标签预测，用这些实例更新模型。

虽然有很多方法用来处理非平稳环境下的有限标记数据流，仍然有一些问题需要解决。在半监督环境下检测概念漂移，检测效果会受到标记样本的影响。当标记样本过少时，仅仅利用有限标记样本的分类准确率检测概念漂移是不可靠的。如何在半监督环境下，同时考虑到无标记样本和有标记样本检测概念漂移，及时对模型进行更新，提高模型的分类性能是当前需要解决的问题。

主动学习是处理缺少类标签数据流的有效方法[15]，因为它可以选择信息最丰富的样本添加标签，构建最佳预测模型，节约标注成本[16]。目前，在线分类技术与主动学习相结合已成为数据流分类的有效方法之一[17]。结合主动学习，开发出稳定高效的，并且能在有限内存下工作的在线分类模型是当前基于主动学习的分类算法所面临的严峻挑战。

本文提出了一种基于聚类的主动学习方法（CALC）实现数据流分类。CALC框架有三个模块，初始模型构建、分类、在线更新。在初始模型构建阶段，利用k均值聚类算法将初始训练数据划分为k组，计算它们的聚类特征形式的统计汇总，然后利用微聚类（MC）保存这些特征。在分类阶段，为了应对概念漂移和类标签不足问题，提出了一种基于聚类距离和聚类纯度的微聚类主动学习框架，利用新的混合标注策略选择部分实例标记后重新训练模型。在模型更新阶段，定义了指数衰减函数，计算模型中的微聚类随时间变化后的权重公式，并通过合并或删除操作创建新的微聚类空间，从而得到新的分类模型。

本文的主要贡献如下：

（1）针对概念漂移和样本标记不足的数据流分类任务，提出了一个基于聚类的主动学习框架。

（2）采用基于微聚类的距离与纯度的惰性学习框架进行分类，利用微聚类中心与实例之间的距离设计一种新的不确定性策略，与随机策略结合得到混合查询策略，查询最值得标记的数据，更好地应对概念漂移。

（3）提出基于微聚类的模型自适应调整方法，设计一种相似性规则合并微聚类，删除过时微聚类，通过维护微聚类权重实现模型的动态更新。

1 相关工作

本文主要研究对于概念漂移数据流的一种基于聚类的主动学习方法。接下来对概念漂移数据流的分类方法、基于主动学习的数据流分类方法以及一些半监督分类方法进行回顾。

1.1 概念漂移

数据流中概念的经典定义是一组对象的集合，这并不符合数据流的特点。现有的大部分文献用概率定义概念。Gama等[18]用数据的联合概念分布p(x,y)表示概念，x表示d维特征向量，y表示相应的标签。数据分布由于某些因素的影响会随着时间的推移而变化，为了具体地描述这种变化，将Pt(x,y)定义为t时刻的联合概率分布。如果Pt(x,y)≠Pt+1(x,y)，说明在t和t+1 以内的时间段发生了概念漂移。联合分布用贝叶斯理论表示为Pt(x,y)=Pt(x)Pt(y|x)。从概率论的方面来分析为何会产生这种现象，原因可分为两类：（1）先验概率P(x)发生了变化，而条件概率P(y|x)没有改变，此时决策边界并没有发生变化，这种现象称为虚拟概念漂移；（2）条件概率P(y|x)发生了变化，无论先验概率P(x)有没有发生变化，决策边界都会改变，降低分类器的分类准确率，这种现象是真实概念漂移。Zliobaite 等[15]根据数据分布如何变化，将概念漂移分成了渐变式、突变式、增量式和重现式概念漂移四种类型。

（1）渐变漂移：渐变漂移的变化范围比较小，需要长时间才能观察到发生了改变，在概念漂移发生前后，概念是极为相似的，所以对分类模型的准确率影响较小。

（2）突变漂移：突变漂移是在较短时间内，数据流中的数据分布突然改变，这种变化具有瞬时性，会导致分类模型的准确率迅速降低甚至失效。这就需要模型能够及时应对这种漂移，更新模型以适应变化后的环境。

（3）增量漂移：增量漂移意味着概念以增量式变化。与渐变漂移类似，短时间内数据分布变化不大，当发生变化时，数据由多个数据分布产生，各个数据分布之间差异性较小。

（4）重现漂移：重现漂移是经过一段时间后，以前出现过的概念重新出现。现实生活中有很多例子，例如以前人们关注的一个话题，在某一个特定的时间，又重新变成热点话题。历史数据可以作为处理这种概念漂移的有效方式，重新利用以前学习过的模型而不用重复训练，避免了资源的浪费。

Bifet 等[19]提出基于可变大小滑动窗口的概念漂移主动检测方法（adaptive windowing，ADWIN），通过比较两个子窗口之间的错误率均值的不同来判断是否发生概念漂移。Nishida 等[20]提出了基于统计检验理论（statistical test of equal proportions，STEPD）检测概念漂移的方法，通过比较局部训练样本的分类准确率和全部样本的分类准确率来检测漂移，准确率一样则数据分布稳定，反之则发生了漂移。还有一些方法通过更新分类器适应概念漂移。Street 等[21]提出了流集成算法（streaming ensemble algorithm，SEA），该方法是一种基于数据块的集成分类算法，不断用最新的数据块去训练新基分类器，集成中的最大基分类器数量是固定的，一旦达到这个数量，将用新的分类器替换集成中最差的分类器。Wang等[22]提出了一种基于准确率加权集成算法（accuracy weighted ensemble，AWE），与SEA 不同的是，AWE 更新基分类器的权值是利用最近到达数据块上的分类准确率。

上述方法属于有监督分类方法，所有训练样本都是被完全标记的，并且这些标签立即可用，真实标签可用来判断分类是否正确，从而得到分类准确率，利用分类准确率检测概念漂移。但是在现实情况下，只有少量标记的样本存在，大量样本都是无标记的。由于数据流高速、海量的特性，人工标注所有样本是不切实际的，于是很多半监督分类方法被提出以解决该类问题。

1.2 基于聚类的分类方法

Widyantoro 等[23]提出了一种用于扩展不完全标记数据流的新计算框架。将少量带有标记的数据流作为输入，然后应用半监督技术对未标记数据流进行标记，由此扩展之前的少数标记数据流形成新数据流。概念漂移检测器是在新数据流进行检测的。Masud 等[10]提出基于聚类的分类模型（realistic stream classifier，ReaSC），数据流被划分为若干个块，块中的标记样本是有限的。利用聚类创建k个簇，对这些簇进行统计信息汇总得到微聚类，在微聚类上应用标签传播技术标记没有标签的微聚类，微聚类的集合构成了分类器。这些方法利用半监督技术自动标记无标签样本，并未获取这些样本的真实标签，无法判断赋予样本的标签与真实标签之间的关系。从而这些方法只适用于类条件分布不变的情况，即无法处理真正的概念漂移。

基于聚类的数据流分类方法利用聚类算法获得聚簇集合（或者将这些聚簇进一步划分为微簇），样本的统计信息可以通过聚簇来反映，这些信息体现了数据分布的局部特征和全局特征[4]。所以聚类适用于数据流中的样本标签不足的情况。为了应对概念漂移，研究者们在聚类的基础上提出了很多新的算法。

Hosseini等[24]提出一种对半监督环境中非平稳数据流的实例进行分类的集成算法（semi-supervised pool and accuracy-based stream classification，SPASC），旨在识别数据流中重现概念漂移。该算法维护一个分类器池，将聚类获得的簇集合作为基分类器保存在分类器池中并赋予权值。通过计算新到达数据块与每个基分类器的相似性判断是否发生概念漂移。Casalino等[25]提出一种基于增量自适应模糊聚类的数据流半监督分类算法（dynamic incremental semi-supervised FCM，DISSFCM）。该算法基于模糊C-均值（fuzzyC-means algorithm，FCM）对数据进行聚类，利用聚类提取数据结构进行分类。对于新到达数据块中的每个样本，预测类别为距离该样本最近的簇的类别。为了更好地应对概念漂移，利用半监督模糊C-均值（semi-supervised FCM，SSFCM）将已经得到的聚类原型与新数据块相结合，得到新的模型并计算每个簇的重构误差，如果重构误差值超过容差值时，表明当前簇的数量不足以有效地表示当前数据，将相应的簇划分为两个簇。Zheng等[26]提出了一种处理重现概念漂移和新类数据流的半监督分类框架（semisupervised classification on data streams with recurring concept drift and concept evolution，ESCR），框架建立在由多个基于聚类的分类器组成的集成模型上。当检测到不是重现概念漂移时，通过部分标记实例更新模型，根据分类器置信度分数选择少数实例标记：（1）置信度分数小于等于阈值，获取该实例的真实标签并将其添加到已标记数据实例集合中；（2）置信度分数大于阈值，模型预测该实例的标签并将其添加到未标记数据实例集合中。根据这两个集合训练新的模型。

上述聚类方法都是用于数据流分类的半监督方法，数据在以块到来的过程中，少量数据含有标记，某些簇所包含的数据可能全部无标记，不能体现出数据流的数据分布，从而影响模型的分类性能，所以需要某种策略查询能够体现数据分布的最有价值样本，利用这些有价值的样本更新分类器，提高分类性能。

1.3 基于主动学习的半监督分类

主动学习是利用采样策略，挑选一些重要的无标签样本交给专家标记，利用标记后的样本训练模型。标签请求策略的好坏决定了主动学习方法的性能[17]。主动学习中经典的标签请求策略包括不确定性策略、随机策略和混合策略[16]。不确定策略基于模型对实例预测的不确定性程度选择实例，重点是不确定度的计算。随机策略是从数据流中随机选择实例进行标注，代表着实例空间中任何区域的实例都有可能被选中，与不确定策略结合可以用来提高不确定策略的准确性。混合策略是结合随机策略和不确定策略的标注策略，是用来检测潜在概念漂移的有效方法。

李南[27]提出了一种基于聚类假设的数据流分类算法（a clustering assumption based classification algorithm for stream data，CASD），该算法利用主动学习，当新实例x被分类后，判断x是否被任意一个模型簇覆盖，如果没有被覆盖或者是处在模型簇边界时，对x进行标记。Haque 等[28]提出了一个半监督框架（efficent concept drift and concept evolution handling over stream data，ECHO），利用基于k-NN 类型的聚类组成集成分类器，提出关联和纯度来计算分类器的置信度，置信度的大小决定是否对样本进行标记。如果分类器对样本分类的置信度小于指定阈值，则请求该样本的真实标签，否则，将分类器预测的标签作为该样本的标签。这些具有标签的样本集合作为训练数据，用来训练新的分类器，替换集成分类器中最旧的分类器。

这些方法只选择决策边界附近的实例进行标注，这对发生概念漂移的数据流来说似乎不太准确，因为概念漂移会出现在实例空间的任何区域。如果漂移的实例不在决策边界附近，该策略选择的就不是变化的实例，从而不能充分应对数据分布的变化。

结合分类方法设计的标签请求策略可以有效提高分类性能。Ienco 等[29]提出了一种基于聚类的主动学习方法（active clustering learning for data streams，ACLStream）。当一批数据来临时，使用聚类方法将它们划分为n个簇。通过宏观步骤对簇进行排序，通过微观步骤对簇中的实例进行排序，以便从每个簇中选取不确定的实例即最有用的实例进行标记。最新到达的一批数据首先利用分类器c1 分类，然后利用ACLStream策略选取将要被标记的数据，最后利用被标记的样本集合更新c1。Zgraja 等[30]提出了一种新的用于漂移数据流分类的主动学习算法，该方法利用了聚类增量思想并且为每个簇分配权重，对于权重最高的簇，根据标记预算，从中随机选择实例进行标记，然后用标记样本集合训练分类器。

上述这些方法通过将数据流分类方法和主动学习方法相结合，即针对在线学习、概念漂移这些分类问题来设计标签请求策略[17]，考虑了不确定性和数据分布，避免了查询策略只关注某些特定区域的问题，验证了良好的标签查询策略能提高分类性能。

2 基于聚类的主动学习框架

在本章中，具体介绍了提出的基于聚类的主动学习框架，CALC 框架有三个模块，初始模型构建、分类、在线更新。第2.1 节介绍了初始化模型的过程，将初始训练数据存储在微聚类MC中。第2.2 节介绍了在线主动学习的分类过程，利用聚类距离和聚类纯度，提出了基于微聚类的主动学习框架。第2.3节介绍了模型的更新过程，考虑到时间效应给分类准确率带来的影响，计算微聚类随时间变化后的权重，移除权重为负或者近似为0 的微聚类，当模型中微聚类的数量达到设定值时，对微聚类进行合并或者删除操作。下面将逐步介绍每个模块。

2.1 初始模型构建

CALC 在算法1 中定义了初始化学习模型的函数。当初始训练数据(Dinit)到达时，利用k均值聚类算法将其划分为k组，不存储这k个聚类，而是计算它们的聚类特征形式的统计汇总，然后利用MC保存这些特征。MC由多个特征组成，定义为MC=(LS,SS,S,N,W,T)。其中LS和SS是分别存储聚类中带有标签的每个类的线性和、平方和，见式（1）；S对应N项类的向量，每项存储聚类中每个类中的实例数量；N是聚类中实例的总数量；W是微聚类在模型更新过程中的权重；T的初始值为0，存储微聚类从上次更新到此刻的时间。为了更好地对微聚类进行处理，利用这些聚类特征计算模型中每个微聚类的半径和中心。见式（2）和式（3）。

算法1初始模型构建

2.2 在线主动学习的分类过程

为了应对概念漂移和类标签不足问题，提出了一种基于聚类距离和聚类纯度的微聚类主动学习框架。

2.2.1 在线主动学习

针对标签稀缺问题，提出了一种新的混合标注策略，将不确定策略与随机策略相结合，处理新到来的实例，对微聚类学习模型进行动态更新使其适应数据流的渐变概念漂移和突变概念漂移。

混合标注策略如图1和算法2所示。当对新到达的未标记实例x利用微聚类学习模型进行标签预测后，判断实例x是否通过混合标记策略请求真实标签。在不确定性策略中，判断x到最近微聚类中心的距离是否大于该微聚类的半径。如果大于半径，说明x不符合当前拟合的数据分布，可能发生了概念漂移；如果等于半径，x可能刚好处于决策边界上，难以对x进行分类。所以需要对这两种情况的x进行标记。在随机策略中，生成0 到1 范围内均匀分布的随机变量ξ，如果ξ小于阈值σ，对没有被不确定性策略标记的实例进行标记，因为概念漂移可能会出现在实例空间的任何区域，不仅是决策边界附近，利用混合标注策略，可以更好地应对概念漂移。后续的标记方法将考虑不平衡数据流的分类，不仅对不确定的样本进行标记，还基于类不平衡比率实现对少数类样本的标记。利用基于边际阈值矩阵的不确定性策略，结合不平衡率动态调整阈值，筛选出难以标记的实例，将其与随机标记策略相结合，提高模型的分类性能。

图1 混合标注策略Fig.1 Mixed labeling strategy

算法2混合标注策略

2.2.2 分类

为了预测新到达实例的类标签，使用了基于微聚类结构距离和微聚类纯度的惰性学习框架。聚类假设表明，距离相近的实例更有可能具有相同的类标签。通过计算微聚类的结构距离，可以得到新到达实例x的k个距离最近的微聚类。纯度是聚类的一种评价指标，通过计算这k个微聚类的纯度，即微聚类中的实例属于同种类标签的情况，可以选择一个相对最优的微聚类。本文定义微聚类的权重为纯度与距离之比，纯度越大，距离越小，则该微聚类的重要性越强，从而为每个新到达的实例选择最合适的微聚类。对于新到达的未标记实例x，搜索离x最近的k个微聚类，利用k个微聚类进行惰性学习（即基于微聚类的k近邻法）。基于微聚类结构距离和微聚类纯度的惰性学习框架对原始的k近邻策略进行了改进，原始的k近邻是给定训练一个数据集，对于新到达实例x，从训练数据集中找到距离x最近的k个实例，这些实例中占据多数的类别即作为x的预测类别。原始的k近邻方法需要存储用于预测的整个数据集，然后得到最近邻域上的最频繁的类标签，由于数据流的潜在无穷特性，存储所有用于预测的数据是不现实的。本文的模型是动态维护一组固定数量的微聚类，从模型中找出距离x最近的k个微聚类。除结构距离以外，本文加入了微聚类的纯度指标，可以进一步找出相对最优的微聚类。通过计算k个微聚类的纯度和结构距离，可以得到相应的权重，即该微聚类在整个模型中的重要性，并选择权重最大的微聚类对新到达实例进行分类。x到微聚类的距离定义为x到微聚类中心的距离，即MCD(x,MCi)，如式（4），微聚类的纯度定义为pur(MCi)，如式（5）。定义微聚类的权重为微聚类的纯度与距离之比。此时该实例的标记label(x)为权重最大的微聚类中类频率最大的类标签，如式（6）。

其中，dist(x,)是给定实例与微聚类中心的欧几里德距离。

其中，表示x的k个最近距离的微聚类。

分类过程如算法3 所示。第4 行利用2.2.2 小节的分类方法对实例分类，第6～19 行判断是否通过混合标记策略请求真实标签。第7～9行请求真实标签，并且预测正确，则增加参与预测的微聚类的权重，并用x与其真实标签y更新参与预测的微聚类Ci，第11～12行如果预测错误，减少参与预测的微聚类权重并将实例及其真实标签存储在缓冲区中。第14～15 行如果实例x到参与预测的微聚类的距离小于微聚类的半径，则用来更新参与预测的微聚类，第17～19 行如果大于微聚类半径，则将x与其预测标签y存储在缓冲区。存储在缓冲区的实例也形成微聚类，并添加到模型中，当只有一个实例时，该微聚类的半径是以启发式的方式设置的，即把最近的微聚类半径的值分配给缓冲区中微聚类的半径。

算法3创建分类模型

2.3 模型的更新

本文提出的模型动态维护一组微聚类实现数据流分类。随着新实例x到达，需要对分类模型进行动态更新以适应可能发生的概念漂移。同时随着时间的增长，旧的微聚类不能预测此时的数据流分布，所以必须考虑到时间变化给分类准确率带来的影响。在数据流中，随着时间的不断增长，数据流的分布可能会由于概念漂移而发生改变，新到达的实例参与模型的更新，从而适应数据流发生的概念漂移。当模型中的某个微聚类长时间没有更新时，说明它与当前的数据流分布不匹配，无法正确地预测当前实例的类标签，模型需要减少过时的微聚类占整个分类模型的权重，以适应当前的数据流环境。因此本文利用指数衰减函数计算模型中的微聚类距离上次更新后的权重，定义如式（7）。其中λ是衰减率，eT是微聚类从上次更新起经过的时间。当模型中的微聚类的权重小于0 或者是近似为0 时，则从该模型中删除该微聚类。本文通过赋予权重动态调整微聚类在模型中的重要性，通常仅有两种情况会触发微聚类权重的降低，即微聚类对实例的标签分类错误，对模型综合性能产生负面影响；或微聚类长时间未被更新，已无法适应当前数据流的分布情况。当微聚类的权重减少到近似为0 或者为负时，表明这些微聚类已经过时，存储的信息不再适用，甚至对模型的正确分类造成干扰，移除它们可以提高模型的执行效率，减少模型的时空开销，而不会对有效信息造成损失。当对x的标记预测正确时，此时距离x最近的微聚类MC的特征更新：

缓冲区形成的微聚类在插入到模型中之前，判断模型中的微聚类数量是否达到了给定的最大边界MaxMC，设置最大边界可以避免由于计算机内存不足而中断对数据流的处理。如果微聚类的数量达到MaxMC时，需要空间来存储新的微聚类。按照微聚类的新旧程度排序，即微聚类最后一次更新起经过的时间大小排序。采用合并或者是删除操作来创建新的空间，搜索距离最近的未标记和已标记的两个微聚类进行合并，如果在分类模型中不存在没有标记的微聚类，则搜索具有最多数量相同标记的微聚类，找到其中最近的两个微聚类，判断两个微聚类的距离与其中最大半径的大小，如果距离比最大半径小，则合并两个微聚类，如果距离比最大半径大，将模型中最旧的微聚类删除。当检测到需要合并时，MC的特征更新如下：

算法4 将所有部分结合得到了CALC 模型。整体框架如图2所示。

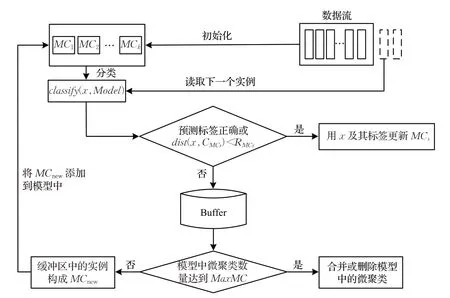
图2 CALC模型框架Fig.2 CALC model framework

算法4基于聚类的主动学习方法实现数据流分类

2.4 算法复杂度分析

（1）时间复杂度。CALC 具有三个部分：初始化模块、分类模块，更新模块。初始化模块是把初始训练数据(Dinit)划分为k个聚类，初始化模块的运行时间是O(Nk|xc),N是模型中类的总数，k是划分为聚类的数量，|xc|是c类实例的总数。初始化模块只运行一次。分类模块算法3 中第4 行的复杂度为O(maxMC)，算法4中4～6行的时间复杂度为O(maxMC)，8～16行的时间复杂度为O(maxMC2)，因为该过程涉及到两个微聚类的合并问题。因此本文提出的算法的时间复杂度为O(NK|xc|+maxMC+maxMC2)，约等于O(maxMC2)。

（2）空间复杂度。模型中维护了一组微聚类，每个微聚类由多个特征组成：MC=(LS,SS,S,N,W,T)，其中LS和SS是分别存储聚类中带有标签的每个类的线性和、平方和的d维矢量，S对应N项类的向量，N、W、T是用来存储单个值，每个微聚类MC的空间复杂度为O(2×V1×d+3),V1×d为维度为1×d的矩阵。本文提出的算法的空间复杂度为O(maxMC×MC),maxMC是模型中微聚类的最大数量。

3 实验结果和分析

本文对CALC算法进行了实验评估，在真实数据集和人工合成数据集上验证了提出方法的有效性。在这一部分中介绍了使用的数据集以及CALC 算法与其他算法的比较结果。

3.1 数据集及评价指标

本文使用了6 种不同的数据流作为数据集。它们具有不同的特征，包括真实数据集和人工合成数据集，它们在概念漂移的性质、速度和数量方面具有不同的属性。如表1所示。

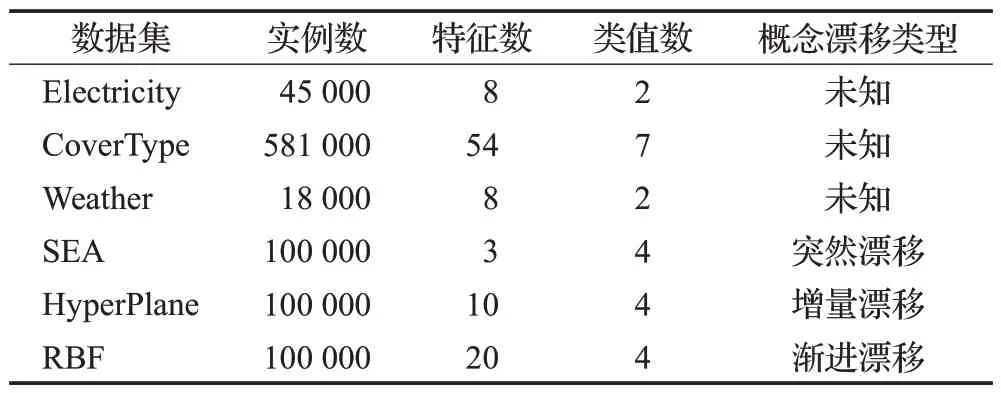
表1 实验中使用的数据集Table 1 Datasets used in experiment

（1）真实数据集

Electricity数据集[31]由45 312个样本组成，每个样本包含8个特征，这些样本分布在2个类别中。8个特征描述了电力需求、市场供应、时间、天气和季节等信息，其类别属性代表了当前时刻的电价对于过去24小时内的平均电价是上涨还是下跌。

CoverType数据集[32]的全称是森林覆盖类型。该数据集包含581 012 个数据样本，这些样本分布在7 个类别中，每个样本有54个特征，描述了土壤和其他相关信息。

Weather数据集[33]全称是内布拉斯加天气预报数据集，收集了50 年的每日天气测量气象数据。由18 159个样本组成，这些样本分为两类，其中31%为下雨，69%是无雨，每个样本包含了8 个与天气相关的特征，例如温度、压力、风速等。

（2）人工合成数据集

人工合成数据集均由在线分析开源平台（massive online analysis，MOA）[34]生成。

SEA 数据集是由MOA 平台上的SEA 生成器生成的包含100 000个数据样本的数据集，有3个属性对应4个类别。该数据集上有三次突变漂移，在2.5×104、4.5×104、7.5×104个实例处。

HyperPlane数据集是由超平面生成器在MOA平台上生成的100 000个数据样本的数据集，有10个属性对应4 个类别，该数据集上有三次增量漂移，在2.5×104、4.5×104、7.5×104个实例处。

RBF 数据集是由MOA 平台上的RandomRBF 生成器生成的包含100 000个数据样本的数据集，有20个属性对应4 个类别，该数据集包含两个渐进的概念漂移，在3.5×104、6.5×104个实例处，其中数据流的概念漂移的变化率为0.01。

本文利用准确率和内存消耗对算法进行评价，分类准确率通常是评估分类器性能的一个重要的标准，统计的是将样本正确分类的比率。实时准确率反映了模型在某个时刻的分类性能，平均准确率反映了模型在整体样本上的分类性能，除了准确率，模型的内存消耗作为辅助的评价指标。

3.2 比较方法

为了验证提出算法的性能，本文把该算法与一些经典的数据流分类算法和最近两年的算法进行比较。下面对这些比较的算法进行了简单的介绍。

在线精度更新集成（online accuracy updated ensemble，OAUE）[35]是一种集成分类方法，将基于精度的加权机制与Hoeffding 树的增量性质结合在一起，该方法对基分类器进行加权，不限制基分类器的大小，也不使用任何窗口，可以对不同类型的概念漂移做出处理。

非平稳环境中概念漂移的增量学习（incremental learning of concept drift in nonstationary environments，LNSE）[36]是另一种分类器集成方法。从连续的数据流中学习，对于新到来的一组数据建立一个基分类器，并将这些分类器与动态加权的多数相结合，不需要考虑概念漂移的性质以及速度。

DWM 是一种集成方法，利用模型分类性能，在集成中动态调整加权基分类器，因此在概念漂移发生时具有更强的响应能力[37]。

Khezri 等[38]提出了一种新的基于性能选择度量的半监督集成算法（a novel semi-supervised ensemble algorithm using a performance-based selection metric to data streams，SSE-PBS）。算法维护一个分类器池，为每个基分类器提供一个权重因子，使用多数加权投票策略对未标记的数据点进行分类。模型更新过程：（1）利用数据块中标记的样本计算基分类器的错误率，从而更新基分类器的权值。并利用新到达数据块训练新的基分类器加入池中，若池满，则替换池中权值最低的分类器。（2）利用集成分类器给未标记样本加伪标记并计算置信度，基于性能的标准选择伪标记数据的子集，添加到当前块的标记数据中以增量更新基分类器。

ORSL是近两年来一种新的数据流分类方法，通过动态维护一组微聚类对传入的数据实例分类，该方法可以在有限的内存下工作。

具有概念漂移的多类不平衡数据流的综合主动学习方法（a comprehensive active learning method for multiclass imbalanced data streams with concept drift，CALMID）是Liu 等[39]在2021 年提出的解决多类不平衡和概念漂移数据流的分类方法。提出一种基于不对称边界阈值矩阵的新型不确定性策略，将该策略与不确定性策略、随机策略相结合解决真实标签不足的问题。使用自适应窗口算法判断是否发生概念漂移，当检测到概念漂移时，利用样本滑动窗口中缓存的样本创建类平衡的训练样本序列，用这些样本训练新的基分类器添加到集成分类器中。

OAUE、DWM、LNSE是有监督学习算法，使用100%标记的数据集，ORSL、CALMID、SSE-PBS、CALC 算法是半监督学习算法，使用20%标记的数据集。

3.3 参数选择

从第2部分可以看出，该算法有3个主要参数：随机标记阈值σ，模型中微聚类的最大数量m，衰减率λ。针对这3 个参数在6 个数据集上分别实验，每个实验重复10 次，取10 次结果的平均值，以确保结果更加准确，找到参数最合适的取值。

随机标记阈值σ的取值由0.01 到0.50，从表2 可以看出，随着阈值的增大，准确率逐渐增大且波动幅度较小，当σ达到0.50 时，分类准确率最高。随机策略中生成0 到1 范围内均匀分布的随机变量，当随机变量小于阈值时进行人工标记，阈值较大代表更大概率得到真实标签，利用真实标签能够发现潜在的概念漂移，及时更新模型适应当前的数据分布。但是实例被人工标记的概率越大，标记成本越高，考虑到标记成本，本文选择σ=0.02 为默认值。

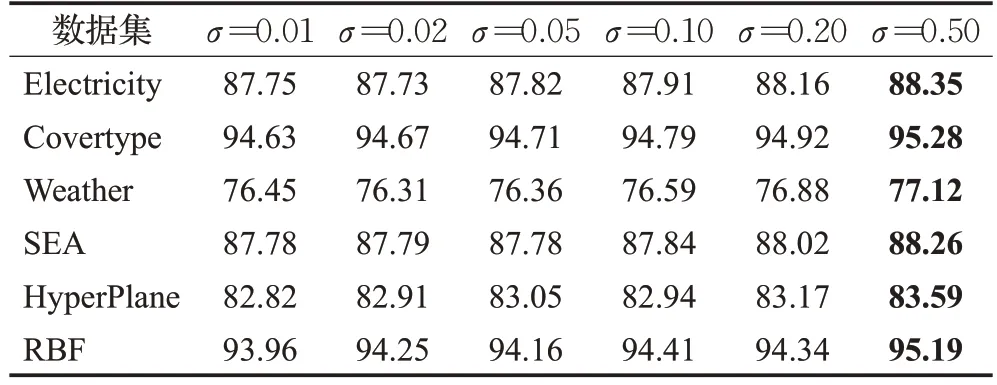
表2 不同参数σ 下的准确率比较Table 2 Accuracy under different σ 单位：%

λ的取值由0.000 001 到0.000 005，从表3 可以看出，λ的最佳取值为0.000 002，从0.000 002 以后，分类准确率呈下降趋势，这是由于随着衰减率的增大，微聚类权重受时间的影响也就越大，过多考虑时间因素，弱化了其他因素对权重的影响，从而影响模型分类准确率，本文将λ的取值设置为0.000 002。

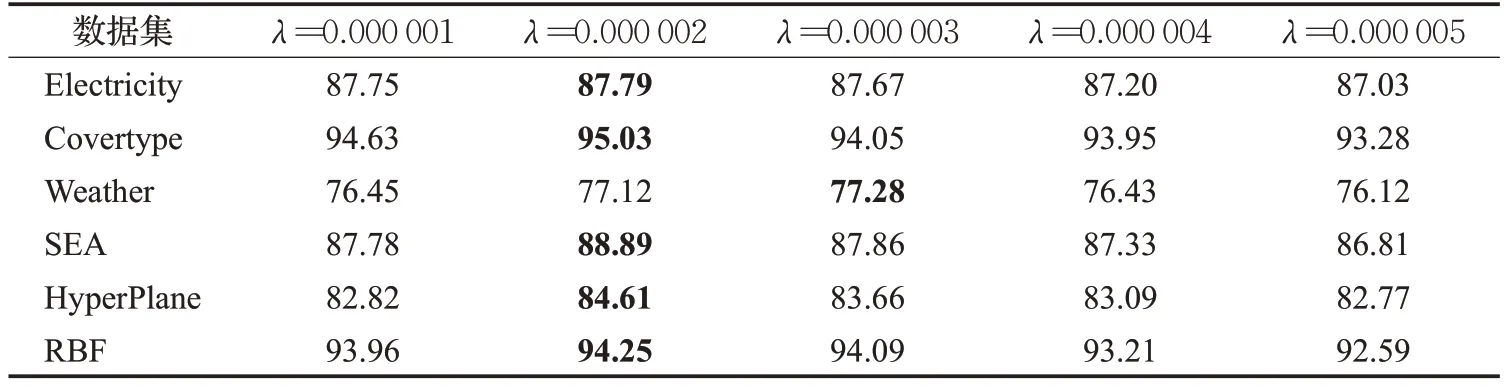
表3 不同参数λ 下的准确率比较Table 3 Accuracy under different λ 单位：%

m的取值由500 到2 500，由图3 可以看出，随着m值的不断增加，分类准确率逐渐增加，当m值达到1 500 时，分类准确率增加趋势放缓。这是由于随着模型中的微聚类数量增多，数据流的变化状态可以得到很好的检测，但是微聚类的数量增多也造成了处理时间变长。为了减少模型的处理时间，本文将最大微聚类的取值设置成1 500。

3.4 实验结果

本文从实时准确率、整个过程的平均准确率和内存消耗的角度在6个数据集上比较了提出的方法与3.2节中的对比算法。对于SEA、HyperPlane、RBF 数据集，实时准确率是指测试点前后10 000个实例的平均准确率，对于CoverType 数据集，实时准确率是指测试点前后50 000个实例的平均准确率，对于Electricity数据集，是前后5 000 个实例的平均准确率，如第10 000 个实例的实时准确率是5 000个实例到第15 000个实例的平均准确率。不同模型的实时准确率比较如图4～图9所示。

图4 显示了在SEA 数据集上，CALC 模型与其他6种模型的实时准确率比较。OAUE的准确率较高，波动幅度比CALC稍大，因为OAUE算法使用固定窗口的实例创建新分类器，以替代模型中最差的基分类器，但是窗口大小并不会根据数据分布的变化而变化，在突变漂移处无法较好地适应概念漂移。CALC、SSE-PBS、ORSL、CALMID 分类性能相对稳定，CALC 与ORSL、DWM 相比，前期准确率相差不大，随着数据流实例的增多，CALC 的分类准确率高于这两种模型，在发生突变概念漂移时，CALC准确率处于平稳或上升状态。因为CLAC不断更新微聚类的权重，使模型能够快速适应当前的数据流环境。

如图5所示，在HyperPlane数据集上，CALC和ORSL基本上没有受到增量漂移的影响，分类准确率呈上升趋势。因为CALC 将预测错误的实例或者在模型边界之外的实例移动到缓冲区中，缓冲区的实例形成微聚类参与模型的更新，可以适应概念的逐渐变化，保证分类准确率的稳定。其他五种模型的分类准确率都有不同程度的波动。虽然DWM 算法的分类准确率随着数据流实例的增长时而产生优于CALC的结果，但是DWM的分类准确率不断波动。因为DWM逐个处理到达实例，能够及时捕捉到数据分布的变化，在处理突变漂移方面具有优势，但是缺少周期更新机制，无法适应增量式概念漂移。

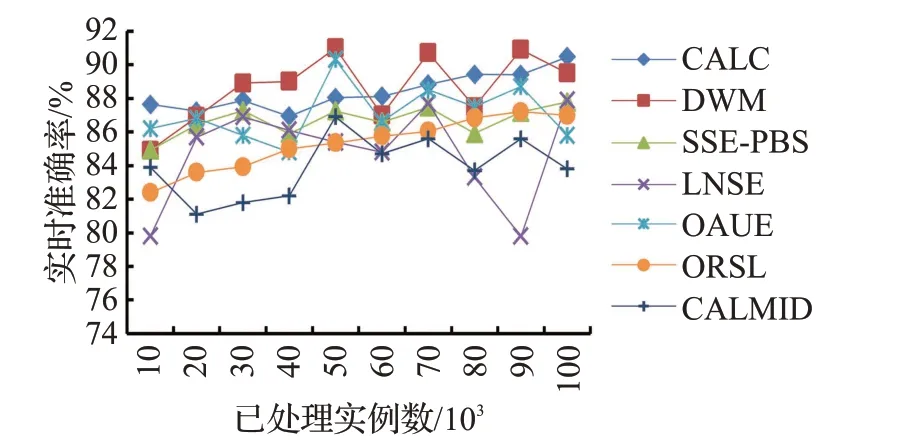
图5 在HyperPlane数据集上的实时准确率Fig.5 Real-time accuracy on HyperPlane

从图6可以看出，在RBF数据集上，CALC、OAUE、ORSL、CALMID不受渐进漂移的影响，始终保持较高的分类准确率，并且CALC的分类准确率略高于OAUE和ORSL。OAUE 能较好地适应概念漂移，DWM 和LNSE的分类准确率较低。CALC动态维护一组微聚类，根据微聚类的权重，能检测到数据流的长期变化情况，删除过时的微聚类，保证模型的周期更新。LNSE 对新到来的一组数据建立一个基分类器添加到模型中，数据块的大小会影响概念漂移的判断，而且没有增量训练已有的基分类器，导致模型处理渐进漂移时存在不稳定的缺陷。

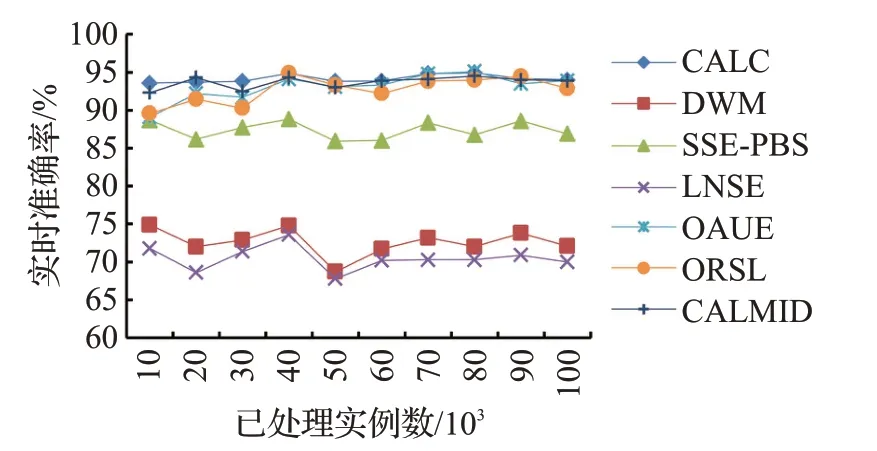
图6 在RBF数据集上的实时准确率Fig.6 Real-time accuracy on RBF

从图7 可以看出，CALC 模型的分类准确率一直比较稳定且属于较高水平，而LNSE模型的分类准确率波动严重，因为LNSE 没有对集成采用剪枝技术，当数据流中概念漂移频繁出现时，模型中的无关旧数据逐渐增多，影响分类性能。

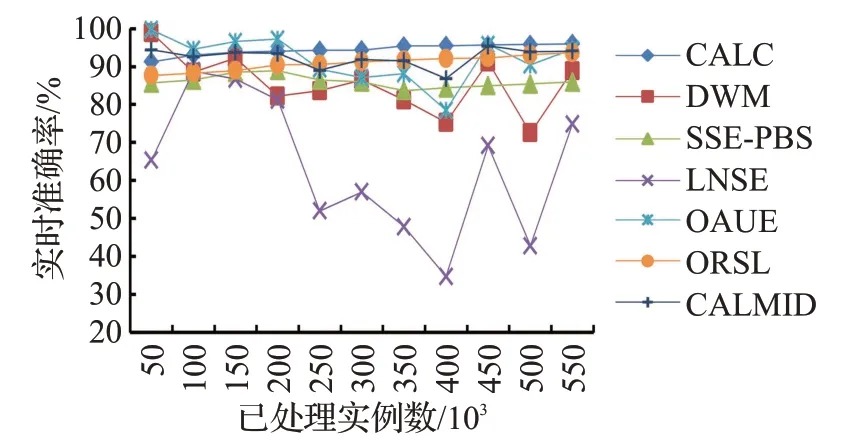
图7 在CoverType数据集上的实时准确率Fig.7 Real-time accuracy on CoverType

从图8 可以看出，在Electricity 数据集上，CALC 算法始终保持较高准确率，当模型中微聚类的权重较低时，删除所有不符合要求的微聚类，模型更新速度快，对概念漂移适应力更强。OAUE模型刚开始占优势，随着数据流实例的增长，CALC 的分类准确率高于OAUE。图9 是Weather 数据集上各个模型的实时准确率比较，CALC分类准确率基本高于其他模型。

图8 在Electricity数据集上的实时准确率Fig.8 Real-time accuracy on Electricity

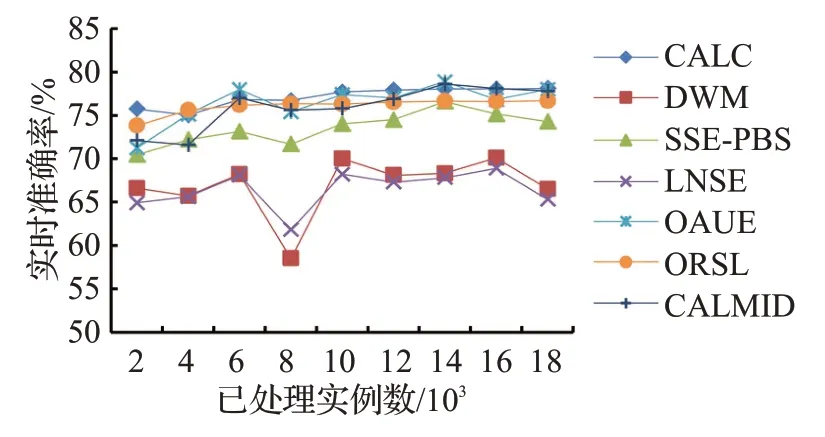
图9 在Weather数据集上的实时准确率Fig.9 Real-time accuracy on Weather

为了更加准确地比较各个模型，考虑到模型的整体分类性能，表4显示了不同数据集上不同模型的平均分类准确率。从表4 能看出CALC 的整体分类性能高于其他模型。所以，不管是在整体分类性能还是实时分类性能上，CALC与其他6种模型相比都有一定的优势。

表4 平均准确率比较Table 4 Average accuracy comparison 单位：%

3.5 内存消耗比较

由于数据流快速实时的不断产生，存储所有的数据是不现实的，所以需要在有限内存下对新到达实例进行分类。为了进一步判断模型的分类性能，实验比较了模型在6个数据集上的平均内存消耗。如表5所示，DWM内存消耗最少，其次是CALC。DWM 是一种在线集成算法，根据最新到达的实例在线更新基分类器的权值，不需要新建基分类器，内存消耗较低。CALC利用了缓冲区机制，缓冲区形成的微聚类会添加到模型中，所以内存消耗比DWM 略高，但是从3.4 节“实验结果”可以看出，CALC能更好地应对概念漂移，分类准确率更高，用少量内存换取更高的分类准确率是可取的。OAUE内存消耗最大，因为OAUE 是基于每个数据块创建一个基分类器，增加了构建分类器的频率和内存消耗。CALMID维持集成分类器、标签滑动窗口和样本滑动窗口，滑动窗口的大小对内存消耗有一定的影响。CALC设置了可存储微聚类的最大数量，当微聚类的数量达到最大值时，对模型中的微聚类进行合并或者删除操作，利用新到达实例在线更新模型，相比于其他的对比方法内存消耗更低。

表5 内存消耗比较Table 5 Memory consumption comparison

4 结语

随着互联网的快速发展，网络规模不断扩大，数据增长速度越来越快，数据流挖掘面临着理论和技术上的挑战。本文针对数据流概念漂移的问题，设计了基于聚类的数据流分类模型和对应的算法。进一步，考虑到数据类标签不足的问题，设计了主动学习混合查询策略，减少了标注成本。本文提出了基于聚类的主动学习算法，改进了在线半监督学习算法，与其他的集成分类算法相比，分类准确率更高而且面对概念漂移时更稳定。

在未来的工作中，将针对数据流中存在的类别不平衡问题进行研究。不平衡数据流中的少数类样本会突然出现，严重影响模型的准确构建。在半监督情况下，少数类样本可能出现全部无法获取真实标签的情况，影响这类样本的学习，无法反映数据的真实分布。接下来将实现不平衡数据流的分类模型，考虑如何设计一种标签查询策略对少数类样本进行标记。