三维复合混沌系统及其在图像加密的应用

于万波，黄蓉荣，王文晋

大连大学 信息工程学院，辽宁 大连 116622

随着网络技术发展，多媒体数字产品与社会媒体得到广泛普及，确保信息在传播和使用中的安全成为研究热点。数字图像作为信息的重要载体有数据量大、数据相关度高等特点，在带来便利的同时，其安全问题也很重要。近些年来，基于混沌的加密技术得到了越来越多的应用，混沌系统具有不可预测性、对初始条件和参数的敏感性等特性[1]。混沌系统按维数分为一维系统和高维系统。一维系统结构简单，生成混沌序列速度快，缺点是密钥空间小、随机性差，在抵御空间重构及其安全性等方面还有不足，比较容易被破译。高维混沌系统有密钥空间大、结构复杂度高等优良特性，可以提高图像加密方案的安全性。

从Lorenz[2]发现空气流动的初值敏感性，混沌理论成为研究热点，很多学者研究基于混沌的图像加密[3-4]。大量实验证明，一维系统用于加密还有安全缺陷，高维系统安全性更高，将一维映射扩展到高维可获得更优良的性能[5-9]。这样的工作还有很多，从中发现函数复合有时可以增强系统的混沌特性，特别是当系统与三角函数复合时。利用三角函数构造混沌系统的研究开始增加，被广泛应用于图像加密[10-13]。

基于这些系统的加密方案已研究多年，也产生了相应的破译方案，持续构造新的混沌系统是必要的。本文构造了一类含有时间t的三维三角函数混沌系统，进一步确认了其混沌特性，混沌特性良好，且生成的混沌序列伪随机性强，同时证明了系统满足Devaney 混沌定义。因此将此系统用于加密图像，分析其加密仿真结果，得出，此方案各项性能指标都非常接近理想值，拥有密钥空间大、密钥敏感性高、安全性和加密效率高等优点。

1 混沌系统介绍

1.1 数学模型

因发现正弦函数作为辅助函数构造非线性迭代系统，其迭代产生混沌吸引子的概率很大[13]。本文通过分析理想情况下将三个均匀的磁场加到空间的三个垂直方向上，带电粒子以速度v从外部进入磁场，当带电粒子受到干扰或者磁场性质改变时，粒子运动的轨迹会发生变化。因此，考虑当磁场边缘不绝对均匀或者有其他扰动时，即系统增加一个干扰项时，系统会产生混沌现象。通过大量实验验证，本文构造了一类包含迭代次数t的三维三角函数复合混沌系统，数学模型用式（1）表示：

式（1）中，x,y和z为系统的状态变量，r1,r2,r3,ω1,ω2,ω3为系统控制参数。大量实验研究发现，当fi(x,y,z),i=1,2,3 是随机生成的线性和非线性函数时，而且系数的绝对值满足很弱的限制条件时，系统就会处于混沌状态。其中扰动函数为线性方程的迭代轨迹（即相图）如图1 所示，系统的迭代轨迹已经看不出明显的纹理，呈现出极端的混沌状态。

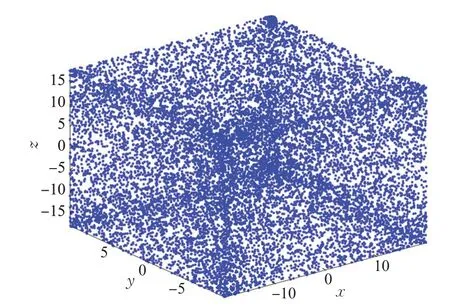
图1 系统混沌现象Fig.1 System chaos phenomenon

1.2 线性函数与余弦函数复合的混沌系统性能分析

余弦函数里嵌套多项式函数构造的系统是混沌的，混沌性能良好。这里三维三角函数混沌系统即式（1）里的fi(x,y,z),i=1,2,3 设为式（2）所示，其中kij＞0，kij也可以是小数，k1.k2k3k4k5中k1∈[1,9]，k2∈[0,9]，k3∈[0,9]，k4∈[0,9]，k5∈[0,9]。

1.2.1 分岔图

分岔图可描述系统中一个变量变化时迭代序列的周期变化。式（3）随机生成系统参数，a3取值为0 到3的数（0 除外），步长为0.06；c2取值为0 到3 的数（0 除外），步长为0.06，得到z关于a3,c2的系统分岔图如图2所示，可直观地观察到混沌现象。

图2 z 关于a3 和c2 的分岔图Fig.2 Bifurcation diagram of a3 and c2 with respect of z

1.2.2 Lyapunov指数图分析

Lyapunov指数越大，混沌特性越强，系统有15个参数，选ω1作为控制参数，a1,b1,c1,a2,b2,c2,a3,b3,c3取0到1 之间的随机数，r1=20,r2=10,r3=18,ω2=320,ω3=360，将ω1从0 提升到300，步长设置为1。计算并绘制ω1的指数图见图3。可看出，混沌区间大，随机性强，表现出更复杂的混沌动力学特性。

图3 关于ω1 的Lyapunov指数Fig.3 Lyapunov exponent diagram of parameter ω1

1.2.3 系统周期点导数分析

混沌定义都与混沌的导数或系统的改变率有关，函数在周期点处的导数必须满足一定条件：一元连续可导函数如果混沌，其n周期、点处导数乘积的绝对值必大于1。二元连续可导函数构成的系统如式（4）：

表1 不同周期点的导数之和Table 1 Sum of derivatives at different periodic points

1.2.4 谱熵分析

谱熵（SE）是分析混沌序列结构复杂性的方法。由于系各个维度相似，为便于SE 的计算和与其他系统的复杂性进行比较，选择一个维度表示。图4 显示了SE的结果以及与Logistic图的对比。本文系统的三角函数图的高复杂度区域范围大于Logistic 图，SE 值更大，混沌映射序列具有较高的复杂性和随机性。

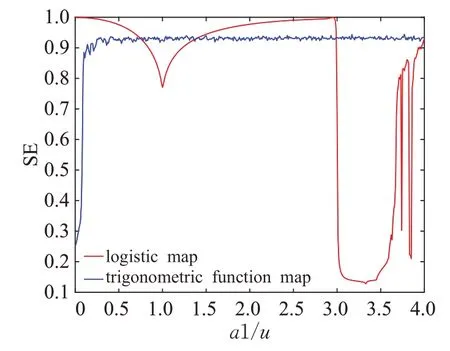
图4 谱熵结果Fig.4 SE analysis of trigonometric

1.2.5 0-1测试

文献[14]提出0-1 检验，是验证系统是否混沌的二元检测方法。0-1测试结果如图5。K值趋近1，参数范围大于Logistic映射，本系统有良好的混沌行为。

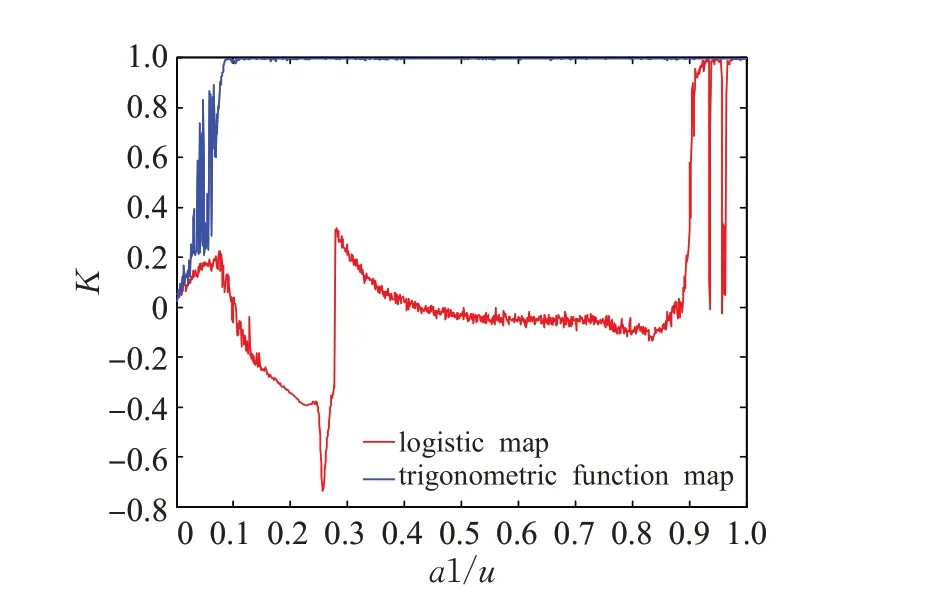
图5 0-1测试结果Fig.5 Results of 0-1 test

1.2.6 NIST测试

NIST SP800 实验由15 个实验组成，用于描述伪随机序列的质量。对系统生成的序列进行测试，结果如表2所示，该序列通过了所有测试。系统生成的伪随机序列具有足够的随机性，能满足加密算法的要求。

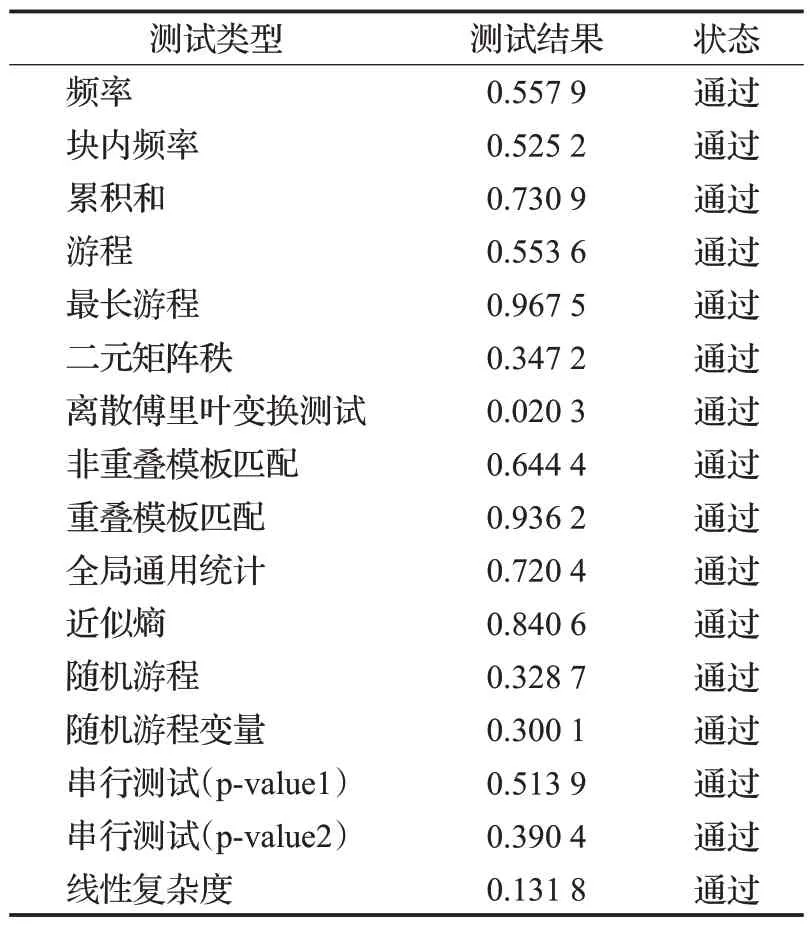
表2 NIST测试结果Table 2 NIST test results

2 余弦函数嵌套多项式函数构造系统的Devaney混沌证明

经典的混沌定义即Li-Yorke 和Devaney 混沌定义。Li-Yorke混沌是抽象的数学定义，不能直观反映随机性，判断条件缺乏直观性。Devaney混沌定义更加直观，某些情况，Devaney 混沌更加混乱。拓扑意义下Devaney 混沌定义：有界闭域(X,d)的映射f:X→X满足以下三个条件，则称为满足Devaney混沌：

（1）拓扑传递，即对于任何的两个开基U,V∈X存在自然数k，使得f k(U)∩V≠∅；

（2）周期性密集，即在X中有稠密的周期轨道，即f的周期点集在X中是稠密的；

（3）初值敏感，即存在δ＞0，使得对于任何x∈X与x的任何一个邻域B，在y∈B和自然数k满足。

然而，Banks等[15]证明了若同时满足条件（1）和（2），则条件（3）一定成立，即Devaney 混沌定义的三个要点之间不是相互独立的，所以只需考察条件（1）和（2）。下面分别对本文系统的一维映射g(x)=rcos(f(x)（)r为常数）和其组成的二维映射展开，进行分析和证明。

2.1 一维映射的Devaney混沌证明

证明映射g(x)=rcos(f(x))满足Devaney混沌定义，只需分别证明一维映射的拓扑传递性和周期点稠密性。

2.1.1 拓扑传递性分析

Zhu 等[16]提出基于正弦-余弦复合系统的混沌模型框架，证明该框架满足对初始值、拓扑传递性和周期点密度的依赖性，参考此拓扑传递性证明思路，证明一维映射的拓扑传递性。将映射的定义域依据k次迭代期间gk(x)的最大值和最小值分为两部分：={x|gk(x)=1}和={x|gk(x)=-1},k=1,2,…，先对集合进行证明，同文献[16]的证明思路，同理可得到两种gk(x)的图像和其折线处理后的图像如图6（a）、（c）和图6（b）、（d），所以一维映射的最大点和最小点都是密集的，对于任意两个开基U⊂[-1,1]，V⊂[-1,1]，一定存在正整数k使得区间U的长度大于lk，所以对于gk(U)=[-1,1]可以满足gk(U)∩V≠∅，最终可以证得一维函数映射是满足Devaney混沌的拓扑传递性的。

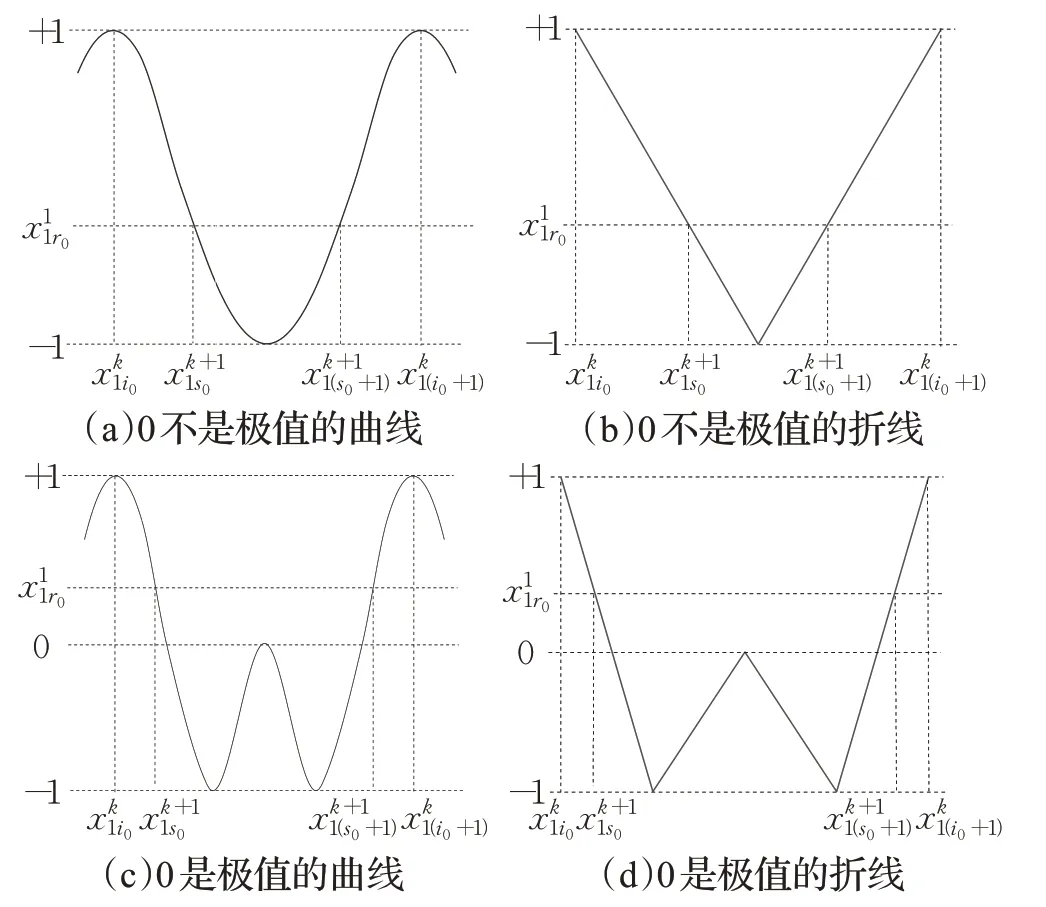
图6 gk(x)的两种曲线及其折线Fig.6 Two kinds of curves of gk(x) and their broken lines

2.1.2 周期点密集分析

周期点密集要求在X中有稠密的周期轨道。如图7，设置参数a1=300,b1=1.2,c1=3,初始值x0=0.3,y0=0.5,z0=0.6，绘制出来的曲线y=gk(x)和直线y=x的相交点就是一个周期点。由2.1.1小节的证明中可得一维映射的最小点和最大点都是密集的，因此，在集合中任意一个点的任意一个足够小的邻域中都有f的周期点，所以映射的周期点是密集的。

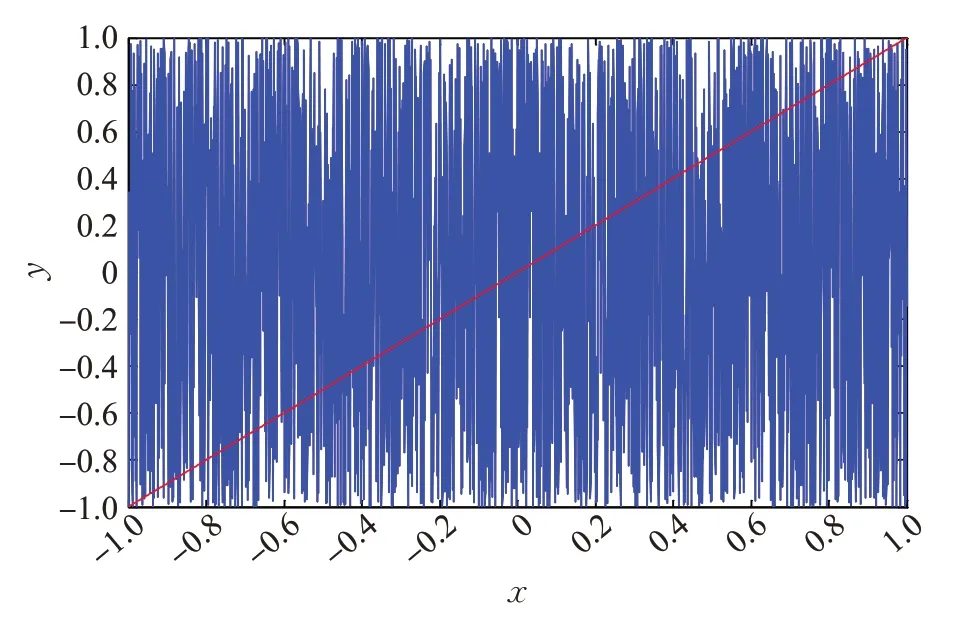
图7 周期点图Fig.7 Diagram of periodic point

通过本小节分析，证得系统的一维函数映射满足下述条件：拓扑传递性和周期点稠密性，所以亦会满足初值敏感性，一维函数映射自然满足Devaney混沌。

2.2 二维系统的Devaney混沌证明

对二维情况分析，首先分别绘制z1=f(x,y)=cos(a1×x+b1×y)和z2=g(x,y)=cos(a1×x2+b1×y2)两个函数的图像，x取值为-1 到1的数，步长为0.01，y取值为-1 到1，步长设置为0.01，绘制的图像如图8。当函数图像曲面的偏导数绝对值增大的时候，随着迭代次数的增大，得到的区域就会扩大，这个较大的区域再作为x-y平面上的区域，如此下去，函数自然会满足拓扑传递和周期点稠密性。

3 加密算法

大多数混沌图像加密方案具有很高复杂度，算法过于繁琐，冗余度比较高，限制了时间效率，不利于实时处理。鉴于此类系统混沌特性很强，衡量加密质量和效率，直接采用提出的高维混沌系统，利用系统生成混沌序列，用此序列对图像的像素值进行扩散从而完成对数字图像的加密，保证加密质量的前提下，大大提高了加密效率。对于大小为M×N的明文图像P，加密算法的设计思路如下，加密流程图见图9。

图9 加密流程图Fig.9 Flow chart of encryption

本文加密算法优势在于本文混沌系统进行加密，其运动轨迹复杂，无繁琐的加密过程，可实现快速加密的同时还保证加密的质量。同时由于系统具有众多的控制参数，导致其密钥空间大大增加，很大程度地增强了图像加密的安全性。解密和加密过程具有相同机理，解密时即向加密过程相反的操作。

4 实验结果及加密效果分析

4.1 实验结果

实验用式（3）三维混沌系统，计算机配置是Windows10操作系统，2.30 GHz处理器和4 GB内存，使用MATLAB R2020a仿真软件。三维混沌系统的系统初始值为x0=0.3，y0=0.5，z0=0.6；系统参数设置为r1=20，r2=10，r3=18，ω1=250，ω2=320，ω3=360，a1=1，b1=12，c1=30，a2=0.1，b2=3.2，c2=3，a3=3.1，b3=12，c3=13。对两幅512×512 的标准灰色图像进行了加密和解密实验，如图10可隐藏住明文的相关数据，可见此加密和解密实验的有效性和可行性。

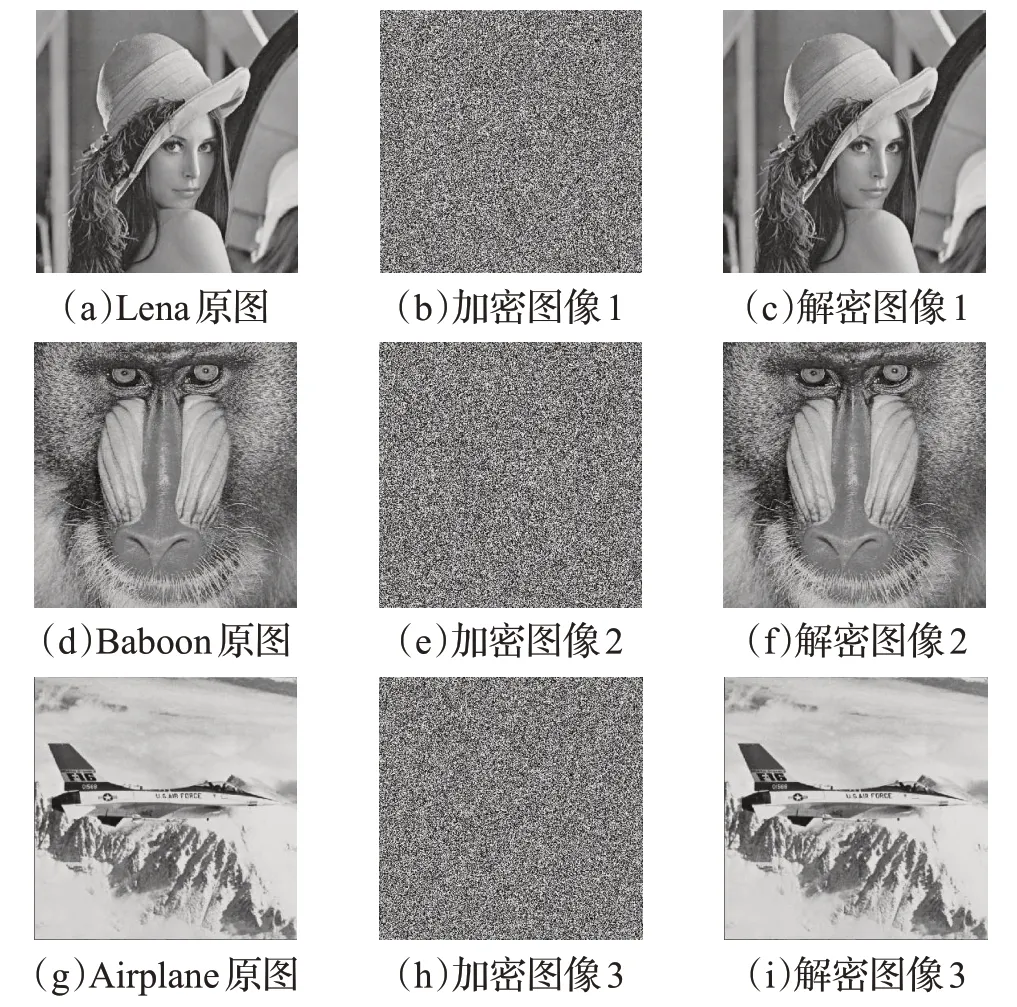
图10 加密实验结果Fig.10 Result of encryption experiments

4.2 加密效果分析

4.2.1 密钥空间

算法密钥主要取决于系统初始条件和参数，范围由混沌系统的初始值x0,y0,z0和系统参数r1,r2,r3,ω1,ω2,ω3,a1,b1,c1,a2,b2,c2,a3,b3,c3共18 个参数构成。实验的仿真设备精度为1014，将参数精确位数设为14位，所以密钥空间大小为1014×18=10252，密钥空间≥2100≈1030可满足安全要求[17]。因此算法密钥空间足够大，暴力攻击无法进行解密。与文献[18-22]的数据对比结果见表3。

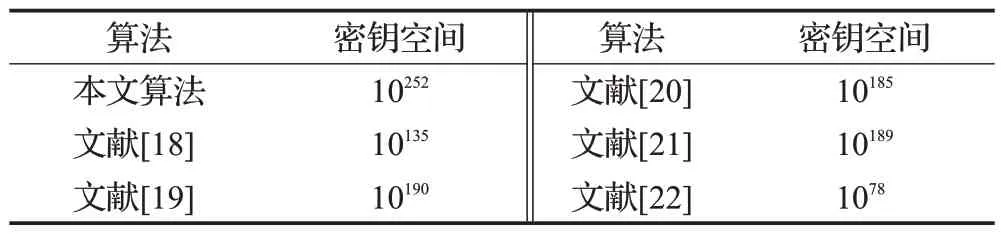
表3 不同加密算法得到的密钥空间对比Table 3 Comparison of key space obtained by different encryption algorithms

4.2.2 信息熵

信息熵可度量图像灰度分布情况，计算得明文和密文的信息熵与文献[18-20，22]的对比结果见表4。

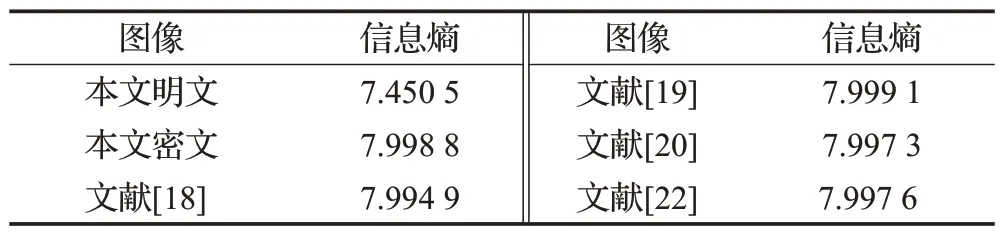
表4 信息熵对比Table 4 Comparison of Shannon entropy

4.2.3 灰度直方图

图像灰度直方图可反映图像的像素灰度值分布。对原始和加密图像评估，如图11 可看出明文直方图有明显的像素值分布特性，加密后的直方图均匀分布，很好地隐藏了明文图像信息，可以抵抗统计攻击。

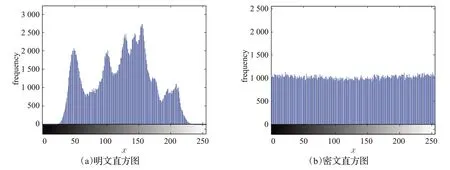
图11 直方图分析结果Fig.11 Histogram analysis results

4.2.4 相关性

相关性表示相邻像素灰度值相关程度，随机选取明文和密文10 000 个像素点，计算水平、垂直和对角线的结果见表5。图12 是加密前后图像在三个方向的散点图。密文没体现相关性，说明破坏了特征信息。

表5 不同加密算法的相邻像素相关系数对比Table 5 Comparison of adjacent pixel correlation coefficients of different encryption algorithms

图12 明文和密文图像在3个方向上的相邻像素对的分布Fig.12 Distribution of adjacent pixel pairs in three directions of plain and encrypted image

4.2.5 密钥敏感性

安全的加密算法要求对密钥有高度敏感性，本小节按照典型的密钥敏感性测试实验用下列步骤来执行：

（1）初始值x0=0.3，y0=0.5，z0=0.6，加密图像。

（2）保证系统其他密钥不变，对初始值分别增加10-14的微小扰动（比如x0=0.300 000 000 000 01，y0=0.5，z0=0.6），再进行解密，实验结果如图13所示。

图13 密钥敏感性测试Fig.13 Key sensitivity test

扰乱后的解密图像不包含原图信息，密钥发生微小改变都会导致解密图像的失败，其与原解密图像的对比数据见表6。因此算法对密钥有高度敏感性。

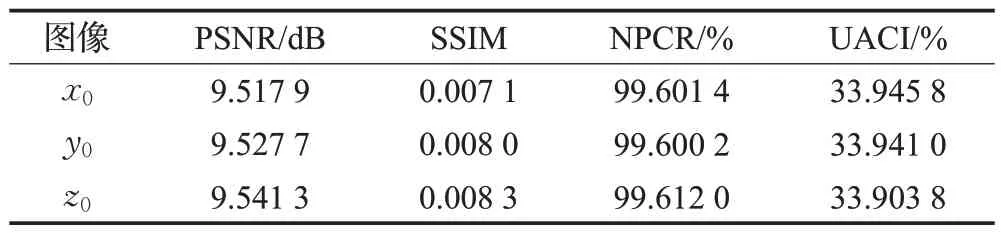
表6 解密图像数据比较Table 6 Comparison of decrypted image data

4.2.6 噪声攻击分析

实际传输中，图像会受到不同程度的噪声干扰。为测试抗噪声攻击的能力，在密文加入不同强度的椒盐噪声和高斯噪声，观察图像恢复情况。

图14和图15分别为不同强度的椒盐噪声和高斯噪声干扰下的解密效果，椒盐噪声的强度分别为0.01、0.05、0.1。高斯噪声的均值为0.01，方差分别为0.000 1，0.000 5，0.001。尽管解密图像有一些噪声，但在视觉上可识别。PSNR的测试结果及比较见表7和表8，可得出该算法在不同强度的噪声攻击下有一定优势。

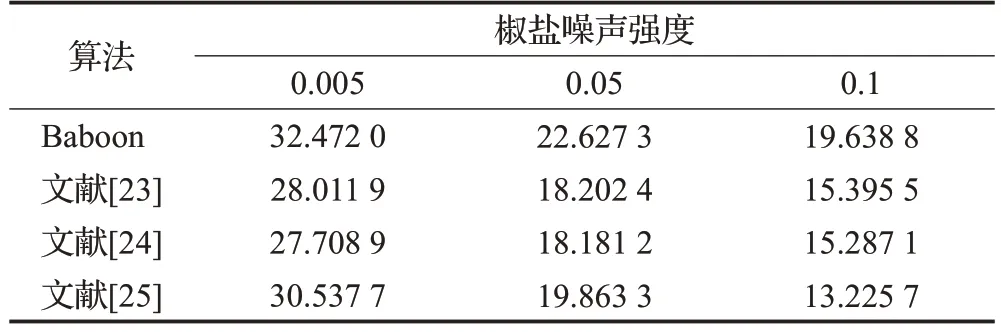
表7 椒盐噪声PSNR测试结果Table 7 Results of Salt &Pepper for PSNR test 单位：dB

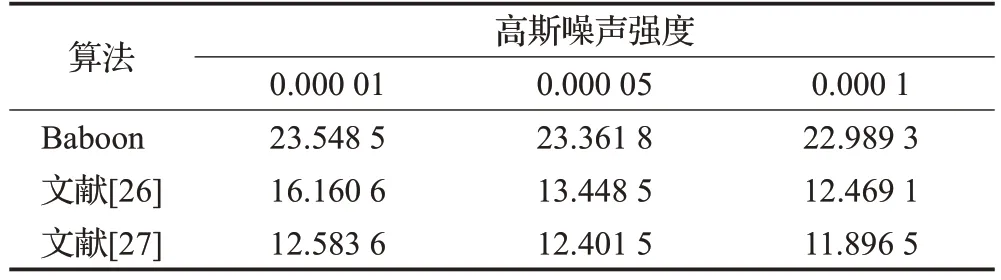
表8 高斯噪声PSNR测试结果Table 8 Results of Gaussian for PSNR test 单位：dB

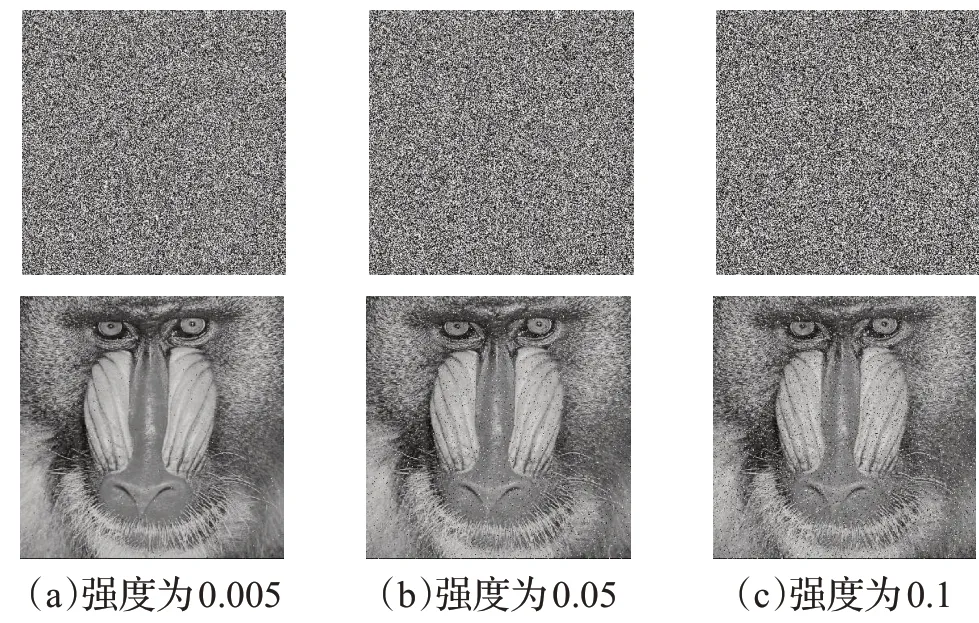
图14 椒盐噪声攻击的解密结果Fig.14 Decryption results of Salt &Pepper noise

图15 高斯噪声攻击的解密结果Fig.15 Decryption results of Gaussian noise

4.2.7 加密速度分析

实际应用中，安全性与速度之间的平衡是加密算法必须考虑的问题。实验的硬件环境为AMD Ryzen 7 CPU，16 GB 内存，1 TB 硬盘；软件环境为Windows 10 Matlab2020a 编译平台。将一幅512×512 大小的灰度图像重复加密1 000次，计算其平均加密速度，测试结果见表9。可看出本文算法有更快的加密速度、更简单高效的系统结构，更适合实际应用。

表9 加密速度对比Table 9 Comparison of encryption time analysis

5 结束语

本文构造了一类三维三角函数复合混沌系统，确定了系统拥有复杂的混沌特性和动力学行为，证明了其满足Devaney 混沌定义。系统生成的伪随机序列也具有足够的随机性，能够满足加密算法的要求。在此基础上，设计了图像加密方案，可以实现快速加密的同时还保证加密的质量，对各项指标进行了计算分析，数值都非常接近理想值，充分体现了该混沌系统在信息安全等领域有更为广阔的前景。