二维对六苯分子团簇中相干激发能量转移过程研究*

方德音 范旭阳 卫岸 王鹿霞

(北京科技大学数理学院,理论物理研究所,北京 100083)

1 引言

近年来,共轭聚集体和分子团簇广泛应用于多种光电器件中,由于电荷及能量转移效率直接或间接影响相关器件的应用,因此其电荷转移和能量转移动力学过程是研究的焦点问题之一 [1−6].对六苯(para-sexiphenyl,6P)分子[7−9]具有平面骨架结构,可以形成离域的π 键,体系能量低,分子稳定性高,其衍生物可以组装成结构各异、功能独特的超分子结构,因此在有机薄膜晶体管[10−12]、场效应晶体管[13]、有机发光二极管[14−16]、光伏电池[17,18]等有机光器件[19,20]中具有广泛的应用.

我们知道在弱场激发作用下,分子聚集体或分子团簇内一般形成单激子态,其相干性较好,但能量转移量低;在强场激发作用下,团簇内多个分子被同时激发[21],能量转移量高,但由于分子间的相互作用,在团簇内形成非局域激发态,同时需要考虑激发能量转移和静电位移的影响,在外场激发过程中涉及多激子能带、多激子协同衰变和超辐射等过程,其相干行为比较复杂,深入理解其多激子激发及相干转移过程对提高相应分子器件的工作效率具有积极意义.

近年来由于分子光刻和金属纳米腔技术的发展[22,23],在局域空间内形成强场已经成为可能,强场激发下分子或分子团簇的吸收、荧光和发射谱实验研究[24−27]已经成为当前的热点,但相应的理论研究相对少得多,主要原因是多激子态在分子团簇内形成的激发位形较为复杂,对其准确描述需要耗费大量的计算资源,且多激子态的量子动力学过程比较复杂,结果难与实验比较.本工作基于密度矩阵理论框架,将局域外场激发或表面等离激元局域场激发都化为激光脉冲激发模型,应用算符的数学平均值近似[21,28,29],考虑分子上的平均激子占据,不考虑多激子占据的具体位形和表面等离激元引发的量子场效应,大大缩减计算量的同时能够正确反映多激子态的量子动力学过程,得到相干能量转移信息.

根据Kasha 理论,分子聚集体和团簇可分为J 型和H 型.J 型聚集体中偶极子头尾相连,呈现负激子耦合,聚合物较单体吸收峰红移,出现荧光增强及超辐射现象.而H 型聚集体中偶极子平行排列,表现正激子耦合,吸收光谱较单体蓝移且出现荧光猝灭现象[4,30].近年来,随着具有荧光性质的染料分子出现,荧光型H 聚集体成为可能,是新一代纳米材料的代表[31−33].且H 聚集可产生强相干激发,在非线性光学等领域应用广泛[34],因此研究H 型聚集体的能量及电荷转移行为尤为重要.

对于H 型6P 分子团簇的理论研究,主要集中在一维分子链的激发能量转移[21]及其与无机界面间的电荷转移[35,36],但许多有机光器件中6P 薄膜为直立分子组成的平面团簇,目前对二维结构中多激子行为的研究较少.本工作以具有平面结构的6P 分子团簇作为研究对象,对其内部激发能量转移过程及相干行为进行研究.由于其高阶激发态的能量远大于两倍的第一激发态的能量,即Efg≫Eeg,我们将其简化为二能级系统,忽略激子-激子湮灭过程[37,38]对动力学过程的影响.第2 节介绍理论模型,第3 节针对不同激发场下多激子态布居数演变过程和团簇的多激子过程展开讨论,第4 节对本文进行了总结.

2 理论模型和动力学方程

采用二能级模型对6P 分子电子态进行描述,引入单分子跃迁算符:

其中|φmg〉为分子基态,|φme〉表示分子第一激发态,在单电子模型下满足关系:=|φme〉〈φme|+|φmg〉〈φmg|=1.这样6P 分子团簇的哈密顿量可以写为

其中,Em表示分子团簇中第m个分子的激发能,可写为

式中,求和部分为分子激发能修正项,表示其余处于基态分子与分子m库仑耦合.第2 项Vmn表示当多个分子被同时激发时,不同分子间的库仑耦合所引起的静电位移对分子激发能的修正,可写为

其中,Jmn表示分子共振跃迁所引起的激发能量转移耦合,可写为

这里忽略了其他非共振跃迁过程的影响.

外场与分子的耦合项写为

其中dm为第m个分子的偶极矩.激光脉冲场E(t)的形式为

其中,n是激光场的方向矢量,ω0是激发场频率.脉冲场包络E(t) 为

其中,τp为脉冲宽度,E0为脉冲场强度.

系统的哈密顿量为

在密度矩阵理论框架下,应用量子主方程可以描述多电子同时激发的动力学过程.若按照传统方法计算,需要考虑各个激发态在分子团簇内的占据位形.计算不同位形下对应的密度矩阵元的动力学过程,计算量随分子团簇中分子数目的增加呈指数增长,我们采用算符的数学期望值近似[21,28,29],只考虑每个分子上电子激发的平均值而不考虑激发态占据的具体位形,研究其动力学过程.

系统的量子主方程为

方程(10)和方程(11) 中的耗散超算符D修正为,量子主方程为

其中分子耗散由分子内转换耗散、分子间激发能量转移引起的振动耗散以及分子退相干耗散三部分组成,分别具有以下形式:

这里,κm为第一激发态的衰变速率,κm→n为相邻分子间振动激发能量转移速率,为分子基态激发态间的退相干速率.

引入分子平均激发态布居数:

以及辅助量Am(t) 和Wmn(t) :

引 入ωm=Em/ℏ,vmn=Vmn/ℏ,jmn=Jmn/ℏ,rm=Rm/ℏ,由于讨论的动力学过程在皮秒量级,且激子衰变速率κm和退相干速率远小于振动激发能量转移速率κm→n,所以忽略κm项以及项,得到以下动力学方程:

结合方程 (3)和方程(4) 给出分子激发能的具体形式:

团簇处于稳态时激发态的电子占据为

为研究多激子团簇的相干行为,引入相干尺寸[39]:

其中,ρmn表示密度矩阵内所有对角及非对角元素,Nmol为团簇内的分子数.当激子间无相互作用时Lρ=1,表明分子团簇内无相干性.

3 结果与讨论

对六苯分子在常温下呈人字形排列[9],选取由59 个6P 分子所组成的圆盘状团簇作为研究模型,如图1 所示.其偶极矩沿分子长轴方向,表现出H 型聚集体特征[4].在脉冲激光场作用下,二维团簇中多个分子被同时激发,形成多激子态,根据相应的量化计算[21],圆盘型6P 分子团簇静电位移及激子能带如图2 所示,其激子能级主要分布在4—5 eV 区域,其他参数列在表1 中,设不同激子间能量转移速率相同κm→n=κn→m=κ.

图1 二维对六苯团簇结构图(a) 俯视图;(b) 沿x 轴侧视图;(c) 沿y 轴侧视图Fig.1.Structure of the two-dimensional 6P clusters: (a) Top view;(b) side view along x axis;(c) side view along y axis.

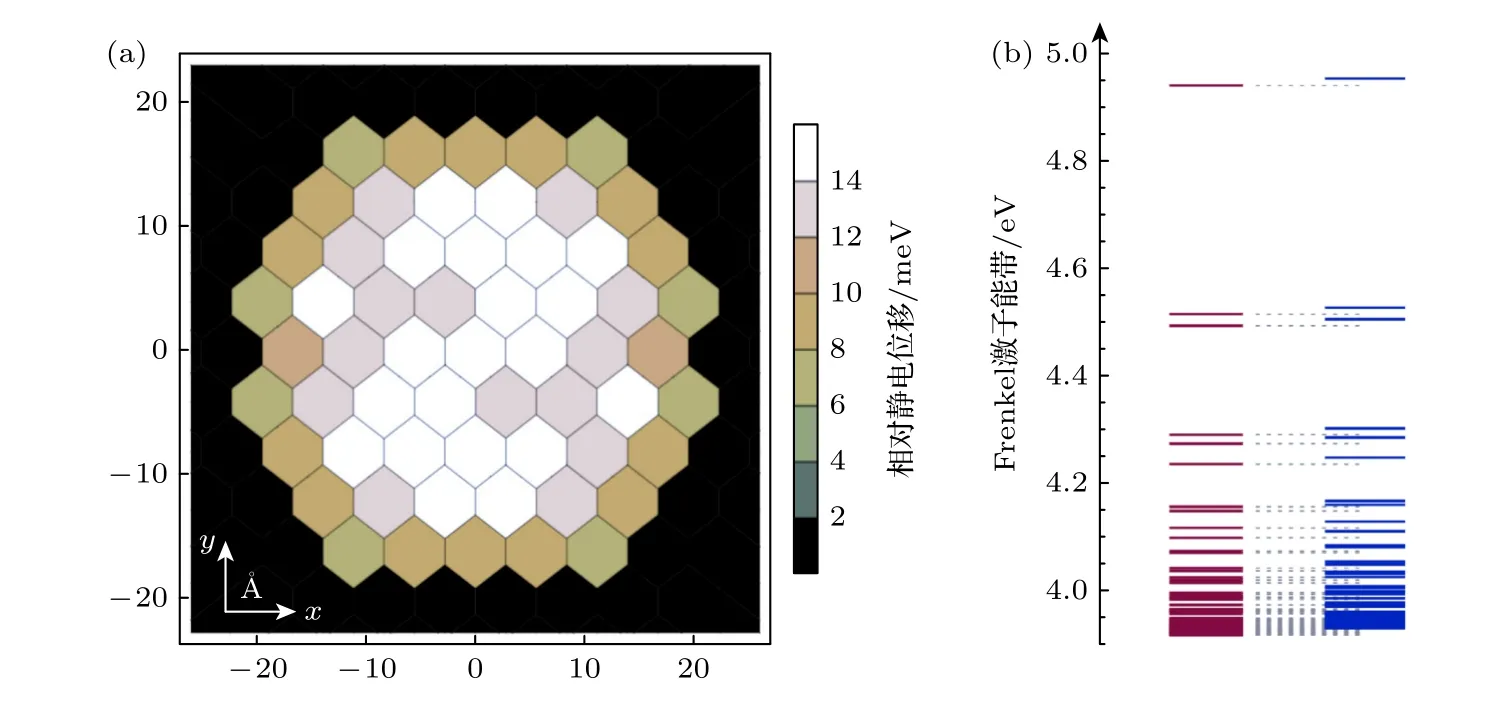
图2 二维对六苯团簇静电位移示意图(a) 分子激发能的相对静电位移;(b) 分子激发能无(红色)及有(蓝色)静电位移时的Frenkel 激子能带[21]Fig.2.Schematic diagram of the electrostatic displacement of two-dimensional 6P clusters: (a) Relative electrostatic shift of the molecular excitation energies;(b) Frenkel exciton energy band without (red) and with (blue) electrostatic shift of the molecular excitation energies[21].

表1 参数设置Table 1.Parameters used.

3.1 光学响应过程

6P 分子团簇的激发和转移过程与外场的能量和脉冲宽度紧密相关.为了深入研究不同脉冲场下,二维6P 分子团簇的激子能带特征,计算了脉冲场能量ap(ap=E0τp)一定时,不同脉冲宽度τp下,6P 分子团簇的光学响应过程,如图3 所示.图3(a)中脉冲场能量较低,ap=5×105ps·V·m-1,发现随脉冲宽度τp的减小,相应峰的峰值增大,展宽增强,但在4.2 eV 附近的低能频段,光学响应峰的峰结构发生变化,由分立的双峰变为有较大展宽的单峰.说明相同脉冲场能量下,脉冲宽度越小,频域内的展宽越大,可以覆盖更多的能级区域,更多的多激子态能级受到激发.图3(b)给出ap=2.5×106ps·V·m-1强脉冲场下6P 分子团簇的光学响应过程.与图3(a)比较可以发现,在脉冲宽度τp较大时,强场激发与弱场激发对应的光学响应相差不大,但随着脉冲宽度的减小,强场激发下的光学响应峰出现明显的红移且出现多个共振峰.说明在强场情况下,外场与激子间相互作用产生新的杂化态,表现出明显的多激子效应.为了进一步研究场强对光学响应的影响及其多激子效应,我们给定脉冲宽度,探究不同脉冲场能量下,6P 团簇的光学响应过程.

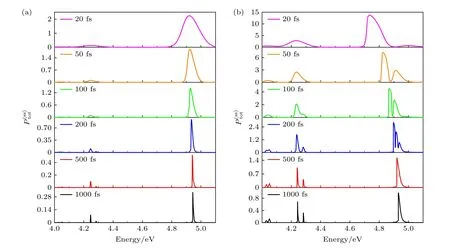
图3 κ=2×1011 s-1 时,团簇内激发态布居 随激光 ℏω0、脉冲宽度 τp 变化 (a) 弱场 ap=5×105 ps·V·m-1 ;(b) 强场ap=2.5×106 ps·V·m-1Fig.3.Excited-state populations in clusters vary with photon energy ℏω0 of the laser and pulse length τp at κ=2×1011 s-1 : (a) In weak fields ap=5×105 ps·V·m-1 ;(b) in strong fields ap=2.5×106 ps·V·m-1.

图4(a)对应τp=1 ps 的长脉冲场,图4(b)对应τp=50 fs 的短脉冲场.由图4(a)可发现当脉冲宽度较大时,共振峰结构不随脉冲场能量的增大而改变,峰值对应的能量与图3(b)中的激子能带结构大致吻合.由图4(b)可以看到,当脉冲宽度较小时,随着脉冲场能量的增大,高能频段的共振峰数目增多,且峰值红移明显.说明在短脉冲场作用下,6P 分子团簇的光学响应过程更多的受到脉冲场影响,随着脉冲场强度增大,激子激发程度增加,外场与激子间发生杂化效应,产生了更多的杂化能级.由于H 型团簇的能级特点,在高能频段电子的布居数增加,多激子效应更为明显.

图4 κ=2×1011 s-1 时,在长脉冲场 (a) τp=1 ps 和短脉冲场(b) τp=50 fs 下,团簇内激发态布居 随激光 ℏω0、脉冲能 量 ap 变 化Fig.4.Excited-state populations in clusters in long τp=1 ps (a) and short τp=50 fs (b) pulsed fields vary with photon energy ℏω0 of the laser and pulse energy ap,κ=2×1011 s-1.

3.2 激子动力学过程

为了进一步研究6P 分子团簇在高斯脉冲场下的多激子行为,应用宽度为50 fs 的短脉冲激发分子簇,图5 和图6 分别给出了 ℏω0=4.2483 eV 和4.9243 eV 时,在t=100 fs (图(a)),200 fs (图(b)),500 fs (图(c))和1 ps (图(d))对六苯分子的激发态布居.可发现在同一激发外场下,6P 团簇的激子局域区域随时间变化不大,对比不同激发态下6P 团簇的激发态布居,可以看到均表现出中心局域的特点,对不同激子态局域特点不尽相同,但由于6P 团簇为二维对称结构,其激子态分布都具有对称性.为了简化描述并理解团簇内分子激发态动力学过程的特点,在团簇内选取6 个典型分子,如图7 所示,研究其动力学特征.

图5 ℏω0=4.2483 eV,κ=2×1011 s-1 时,弱场短 脉冲作用下(ap=5×105 ps·V·m-1,τp=50 fs),4 个不同时刻的分子激发态布居 Pm (a) t=100 fs ;(b) t=200 fs ;(c) t=500 fs ;(d) t=1 psFig.5.Molecular excited state populations Pm at four different moments in the weak field with short pulses (ap=5×105 ps·V·m-1,τp=50 fs),ℏω0=4.2483 eV,κ=2×1011 s-1 : (a) t=100 fs ;(b) t=200 fs ;(c) t=500 fs ;(d) t=1 ps.

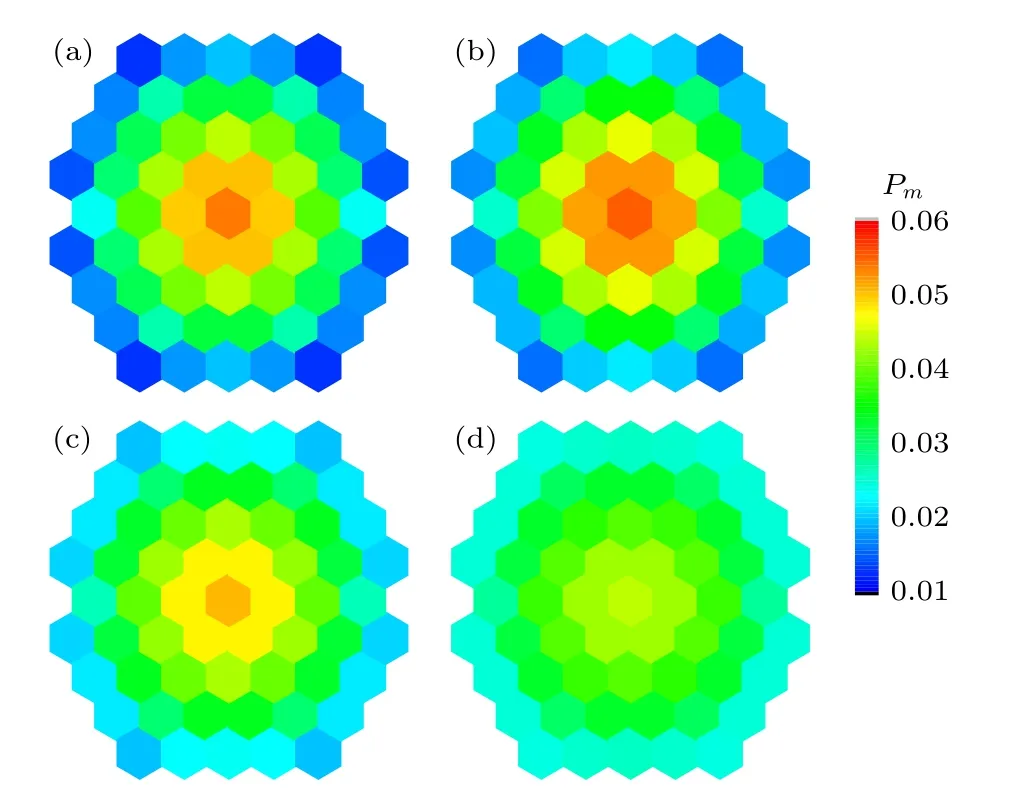
图6 ℏω0=4.9243 eV,κ=2×1011 s-1 时,弱场短 脉冲作用下(ap=5×105 ps·V·m-1,τp=50 fs),4 个不同时刻的分子激发态布居 Pm (a) t=100 fs ;(b) t=200 fs ;(c) t=500 fs ;(d) t=1 psFig.6.Molecular excited state populations Pm at four different moments in the weak field with short pulses (ap=5×105 ps·V·m-1,τp=50 fs),ℏω0=4.9243 eV,κ=2×1011 s-1 : (a) t=100 fs ;(b) t=200 fs ;(c) t=500 fs ;(d) t=1 ps.

图7 二维对六苯团簇选取分子示意图Fig.7.Schematic diagram of selected molecules in twodimensional 6P clusters clusters.

H 型团簇的特点是在光激发作用下电子优先占据高能激子态,图8 给出了6 个典型分子在ℏω0=4.9243 eV 的短脉冲激发下,分子激发态布居Pm的动力学过程.由图8(a)可以看出,在脉冲场激发作用下,对六苯团簇的激子布居数迅速增大,约100 fs 左右达到峰值,之后在激发能量转移的影响下激子布居数不断变化,约6 ps 到达稳态.进一步加大脉冲场(图8(b)—(d))时,研究发现,对六苯团簇激发态布居整体变化趋势与ap=5×105ps·V/m(图8(a))时的情况相近,但随着脉冲场增大,其达到峰值所需时间减少且出现Rabi 振荡,Rabi 振幅随脉冲场增强而不断增大.当脉冲场足够大时,在前100 fs 激子振荡的协同性消失,激发局域性被破坏,出现非局域现象.

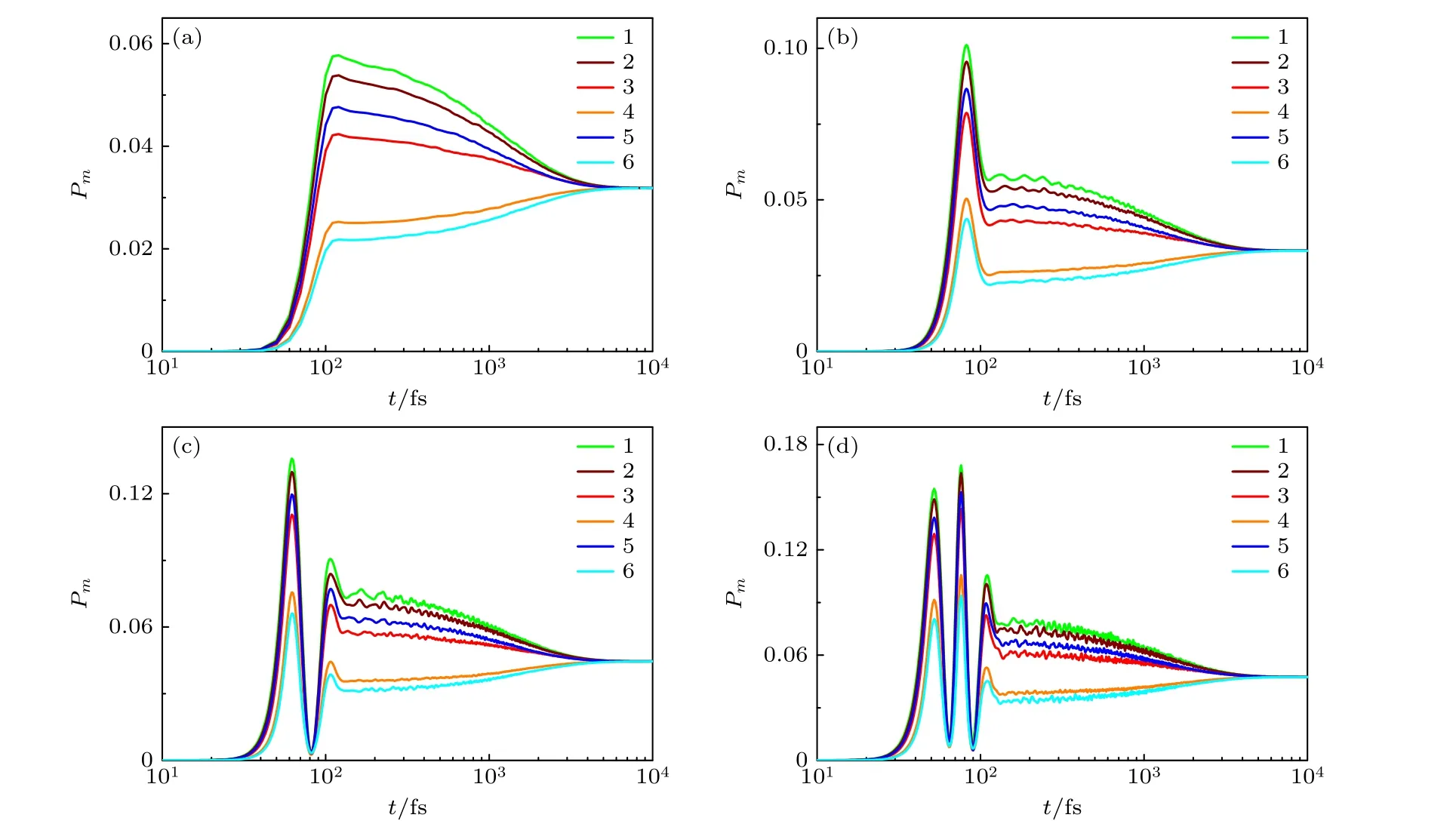
图8 κ=2×1011 s-1 时,短脉冲(τp=50 fs,ℏω0=4.9243 eV)场下,分子激发态布居 Pm随时间的演变 (a) ap=5×105 ps·V·m-1 ;(b) ap=106 ps·V·m-1 ;(c) ap=2.5×106 ps·V·m-1 ;(d) ap=5×106 ps·V·m-1Fig.8.Molecular excited state populations Pm in short pulsed fields (τp=50 fs,ℏω0=4.9243 eV) vary with time,κ=2×1011 s-1 : (a) ap=5×105 ps·V·m-1 ;(b) ap=106 ps·V·m-1 ;(c) ap=2.5×106 ps·V·m-1 ;(d) ap=5×106 ps·V·m-1.

3.3 激子相干

为了进一步研究其相干特性,与图8 对应,图9给出相应脉冲场条件下二维6P 团簇激子相干尺寸随时间的变化.可以看到在场强较弱的时候,激子相干尺寸随时间呈现先增后减的趋势,随着脉冲场增强,在脉冲作用时间内(150 fs),激子相干尺寸出现一个或多个峰,其峰值位置与图9(c)和图9(d)中的波谷对应,说明激子相干与激子布居的非协同振荡紧密相关.

图9 在 κ=2×1011 s-1,短脉冲(τp=50 fs,ℏω0=4.9243 eV)场下,激子相干尺寸 Lρ 随时间的演变Fig.9.Exciton coherence size Lρ in short pulsed fields(τp=50 fs,ℏω0=4.9243 eV) vary with time at κ=2×1011 s-1.

激子相干是非局域激子的一种量子效应,表明激子处于不同分子激发的相干叠加态[40].受脉冲激发及分子耗散的影响,对六苯分子的激子相干态不断变化,相应激子局域范围随之改变,当对六苯团簇处于稳态时,分子间的相干能量转移减少,激子态在每个分子上趋于全同.随着脉冲场增大,激子相干效应增强,Lρ增大,当脉冲场场强较大时,前100 fs 内大量分子在极短时间内发生激子相干,产生瞬态离域现象.

4 结论

基于二维对六苯团簇的结构特点以及能级分布,将分子系统简化为二能级模型,采用算符的数学平均值近似,从量子主方程出发,研究不同脉冲场激发下圆盘状二维对六苯分子团簇的激子动力学过程,并针对其激子布居及激子相干行为进行讨论.研究发现,应用长脉冲激发二维对六苯团簇时,主要表现为单激子态特征,对激发外场的场强变化不敏感.当外场为强场短脉冲时,多个激子同时被激发,形成多激子态且有新的杂化态出现,在光学响应谱上出现了多个共振峰.强度增大,多激子效应明显,杂化能级增多.在短脉冲激发下,分子团簇在不同时刻的激子态布居均表现为明显的对称性.随着脉冲场强增大,对六苯分子的激子态出现Rabi 振荡,当脉冲场达到一定场强时,前100 fs内激子振荡协同性消失,表现非局域特点.从激子相干尺寸角度发现脉冲场增强使相干尺寸出现多个峰,说明激子相干随脉冲场增大而增强,当脉冲场达到一定场强时,脉冲激发过程中大量分子处于激子相干态,出现瞬态离域现象.