基于复合熵和证据理论的抗SSDF攻击协作频谱感知方法

苑申昊, 陈增茂,2,*, 刁 鸣, 孙志国, 孙溶辰

(1. 哈尔滨工程大学信息与通信工程学院, 黑龙江 哈尔滨 150001;2. 哈尔滨工程大学工业和信息化部先进船舶通信与信息技术重点实验室, 黑龙江 哈尔滨 150001)

0 引 言

认知无线电[1]的提出,有效解决了固定频谱资源分配方式导致的频谱利用率低的问题。频谱感知作为认知无线电中最为重要的环节,通过次级用户(secondary user, SU)检测目标频段内主用户(primary user, PU)信号是否存在,在不干扰PU的前提下,合理利用频谱资源。协作频谱感知[2-4]利用多个SU的感知结果进行融合,解决了单个SU感知时受到阴影、衰落等因素影响导致的性能不佳问题。

协作频谱感知中,每个SU将感知信息发送至融合中心(fusion center, FC),FC通过一定的融合准则,对感知信息进行融合和判决,得到最终的判决结果。传统的融合准则可以分为决策融合和数据融合[5](如选择合并、等增益合并和最大比值合并)。

信息融合是协作频谱感知的关键。DS(Dempster-Shafer)证据理论可以在先验信息较少的情况下解决信息融合中的不确定性问题,得以广泛研究。文献[6]首先提出了一种利用DS证据理论进行信息融合的协作感知方法,其性能优于传统的融合准则,但未考虑不同SU所在信道环境的不同,对融合结果产生的影响。文献[7]针对此问题做出了改进,利用SU的信噪比作为权重,修改基本概率分配(basic probability assignment,BPA)信息,从而提升感知性能。文献[8]提出了一种基于证据理论的加权协作频谱感知方法,对不同SU进行可信度权重分配,提高了感知性能。然而,协作频谱感知所在的开放式环境,很容易受到频谱感知数据篡改(spectrum sensing data falsification, SSDF)攻击影响[9-10]。一方面,恶意用户(malicious user, MU)通过篡改其感知信息,向FC发送错误信息,使FC得到错误的判决结果,从而干扰PU正常通信,或者私自占用空闲的频谱资源。另一方面,由于Dempster融合公式存在弊端,当MU发送篡改信息时,会导致FC得到有悖于理论值的结果或失效,对FC判决产生极大的干扰,在证据理论中,这一问题称为证据悖论[11]问题。

目前,已有的解决方法分为两类,一类方法是,FC识别出MU,在信息融合时直接舍弃MU的信息,文献[12]利用“最大最小相似度”区分MU和普通用户,但这种方法存在损失信息量的风险。另一类方法是从减小MU对融合结果影响的角度分析,通过距离函数、信度熵等测度转化为权重,对BPA进行修正,FC对修正后的BPA进行信息融合。文献[13]在本地感知中,提出投影近似法,减少了SU发送的信息量,之后FC采用距离函数转化的可信度降低MU对融合结果的影响,但投影近似法并未从本质上解决不确定信息的分配问题。文献[14]提出了一种新的距离测度,从SU相似性的角度进行权重分配,有效解决了证据悖论问题,但新的距离测度计算较复杂,且并未考虑常见的SSDF攻击问题。文献[15]利用BJS(Belief Jensen-Shannon)散度和信度熵的乘积作为权重,该方法未能解决MU发送和普通用户完全相反的BPA信息时,两者熵权重相同的问题。文献[16]对文献[15]的方法进行了改进,用Lance距离代替了JS散度,但Lance距离公式存在弊端,当两个MU发送BPA为0的信息时,该方法存在失效的风险。文献[17]提出了新的冲突系数,结合模糊熵以及信誉值确定SU的权重,但新的冲突系数并未解决经典冲突系数存在的问题,且忽略了Dempster融合公式的弊端。文献[18]在距离函数的基础上,加入了信誉值更新模型,对SU进行识别,但该方法迭代速度慢,计算较为复杂。

针对上述问题,本文在距离函数和信度熵的基础上,提出一种新的测度——复合熵,通过对距离向量进行信度熵处理,进一步加大MU和普通用户的差异度,降低MU发送的篡改信息在融合判决中的权重。本地感知阶段,为减小信息计算量和传输量,SU只计算对判决有用的信息,并利用SU信噪比调整BPA;融合判决阶段,FC计算SU的复合熵,将复合熵转化为权重,为了避免DS证据理论中Dempster融合公式的弊端,FC利用复合熵转化的权重加权求和BPA,得到最终的判决结果。仿真结果表明,和已有方法相比,本文算法在不同的SSDF攻击类型下,具有较好的感知性能。

1 系统模型

协作频谱感知的系统模型如图1所示,系统由一个PU信号、一个FC、若干个SU和MU组成。协作频谱感知分为本地频谱感知和信息融合两个阶段。

图1 协作频谱感知模型

1.1 本地频谱感知

本地频谱感知采用应用较为广泛的能量检测法,每个SU的频谱感知可以建模为二元假设检验问题。

(1)

式中:H1表示PU信号存在;H0表示PU信号不存在;s(t)为PU发射信号;hi为第i个SU和PU之间的信道增益;n(t)为感知信道内的加性高斯白噪声;yi(t)表示第t个时隙,第i个SU接收到的信号。

根据能量检测法,第i个SU的检测统计量为

(2)

式中:N为采样点数,且N=2TW,T为检测时间,W为信号带宽。当N足够大时(N≥200),检测统计量近似服从高斯分布。此时,检测统计量表示为

(3)

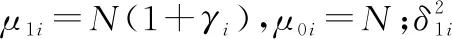
1.2 信息融合

将DS证据理论应用到协作频谱感知中,定义识别框架为Θ={H1,H0,Ω}。根据文献[6]和式(3),计算第i个SU的BPA分别为

(4)

(5)

mi(Ω)=1-mi(H1)-mi(H0)

(6)

利用Dempster融合公式,将所有SU的BPA信息进行融合,得到总的BPA:

(7)

(8)

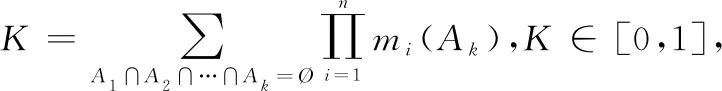
最后,比较m(H1)和m(H0)的大小,得到最终的判决结果,判决表达式为

(9)

1.3 SSDF攻击和Dempster融合公式弊端

证据理论可以解决协作频谱感知信息融合中的不确定性问题,但协作频谱感知所处的开放式环境,往往忽略了MU发送篡改信息对FC判决结果的影响。SSDF攻击方式灵活多变,是协作频谱感知面临的主要威胁。

根据恶意用户发动攻击方式的不同,可以分为Always-Free攻击、Always-Busy攻击、随机攻击3类。Always-Free攻击,简称AF攻击,是指MU向FC发送PU信号不存在的信息,诱导FC做出错误判决,SU接入频谱,对PU正常通信带来强烈干扰,这种攻击本质上是干扰型攻击。Always-Busy攻击,简称AB攻击,是指MU向FC发送PU信号存在的信息,从而在PU信号不存在时,私自占用频谱资源,这种攻击本质上是自私型攻击。随机攻击,是指MU篡改其数据,向FC发送相反的感知数据,既可以干扰PU正常通信,也可以在PU信号不存在时私自占用频谱。混合型攻击是指多个MU发动不同类型的攻击,对协作频谱感知网络造成破坏。

另外,Dempster融合公式存在弊端,当MU向FC发送篡改信息时,会导致FC得到与实际情况相悖的结果,在证据理论中,这些错误信息称为冲突数据[19],这些数据会影响冲突系数K,如果K=1或K值趋近于1,Dempster融合公式便会失效或得到有悖于事实的结果。

2 算法原理

2.1 复合熵

复合熵由距离函数和信度熵组成。

设共有n个二维向量,其任意两个二维向量为m(xa,ya),n(xb,yb),其中,xa,xb∈[0,1],ya,yb∈[0,1],且xa+ya=1,xb+yb=1。这里xi,yi(1≤i≤n)分别对应于协作频谱感知中,第i个SU对假设H1和假设H0的支持度。

定义向量m和向量n之间的距离[20]为

(10)

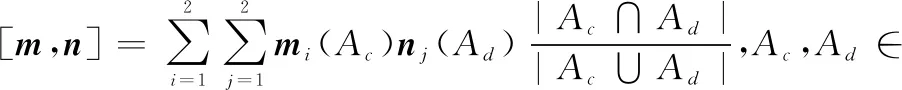
向量之间的距离可以用来描述向量之间的差异度,即距离越小,相似度越高,距离越大,相似度越低。

信息熵用来对信息进行度量,描述信息量的大小。为了更好的适用于DS证据理论,邓勇对香农熵进行了改进,提出了信度熵[21],信度熵的计算方法为

(11)

式中:Hk是识别框架Θ={H1,H0,Ω}的子集,Ω表示不确定信息;mi(Hk)是第i个证据的BPA;|Hk|是集合Hk的元素个数。

在协作频谱感知中,|Hk|只分配给单个元素,此时信度熵和信息熵相同,式(11)可以写为

(12)

信度熵越大,表示SU不确定性越大;反之,信度熵越小,表示其不确定性越小。

信度熵虽然能表明不同SU的不确定性,但MU发送和普通用户相反的BPA时,从信度熵的角度不能直接判断SU是否为MU。

本文从距离函数和信息熵出发,提出复合熵,其基本思想是对SU之间的距离向量进行信度熵处理,MU和普通用户的相对距离大,经过信度熵处理得到的复合熵进一步增大,在FC进行判决时,赋予其小的权重。因此,可以利用不同SU之间复合熵的差异进行权重分配,从而降低MU对判决结果的影响。

复合熵的计算方法如下:

(1) 根据式(10)计算不同SU之间的距离值,得到距离矩阵:

(13)

该矩阵为对称的方阵,即dij=dji(1≤i,j≤n)。

(2) 将矩阵中的第i个行(列)向量定义为第i个(1≤i≤n)SU和其他SU的距离向量:

di=[di1,…,dii-1,dii+1,…,din]

(14)

对距离向量归一化处理,得到新的向量:

(15)

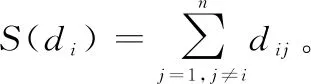
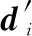
(16)

2.2 复合熵性质

下面对复合熵的性质进行讨论。

性质 1复合熵满足非负性

H≥0

(17)

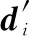
H>0

(18)

复合熵H>0,可以避免接下来将复合熵转化为权重时,分母为0的情况。

证毕

性质 2复合熵满足对称性

证明以3个二维向量m,n,p为例进行证明。这3个向量的距离矩阵为

(19)

计算得到向量m,n,p的复合熵为

(20)

(21)

(22)

式中:Sm=dmn+dmp;Sn=dnm+dnp;Sp=dpm+dpn。

交换m和n的位置,得到新的距离矩阵:

(23)

计算向量的复合熵和式(20)～式(22)相同。同理,交换m和p的位置,计算得到的复合熵仍保持不变。将3个向量引申到n个向量,结论仍成立。

证毕

从以上证明可以看出,复合熵满足对称性,即任意交换向量,不影响向量的复合熵。因此,在计算复合熵时,无需考虑SU的先后顺序。

2.3 算法描述与流程

本文所提基于复合熵和证据理论的抗SSDF攻击协作频谱感知方法流程如图2所示,计算步骤如下:

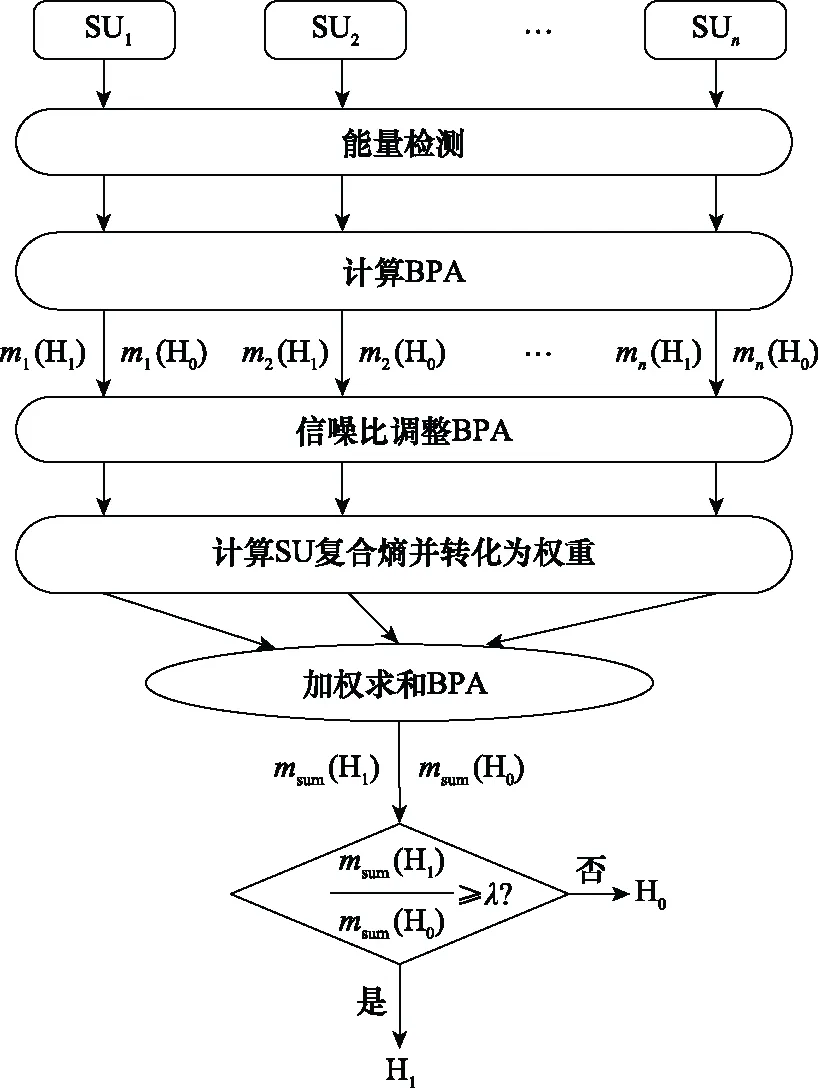
图2 基于复合熵和证据理论的数据篡改防御方法原理

步骤 1每个SU进行能量感知,计算得到mi(H1)和mi(H0)。

步骤 2根据SU感知信道的差异,利用不同SU的信噪比对BPA进行调整,并将BPA发送给融合中心。

步骤 3FC计算SU的复合熵,并转化为权重。

步骤 4FC利用权重对BPA进行加权求和,得到最终的判决结果。

2.3.1 BPA调整

由式(2)～式(5)可以得到每个SU的能量感知和BPA信息。需要注意的是,m(Ω)表示不确定信息,无法为判决提供有用信息。因此,本文算法中,只计算mi(H1)和mi(H0),这样既可以减少本地感知中SU的计算量,同时也可以减少SU向FC发送的信息量。

根据SU所在感知信道的差异,可以利用不同SU的信噪比对BPA进行调整,反映不同SU信道差异对感知结果的影响。第i个SU的信噪比权重为

(24)

式中:SNRi表示第i个SU的信噪比;max(SNR)表示所有SU信噪比中最大值。

调整后的BPA为

(25)

(26)

利用式(13)～式(16),计算SU的复合熵,然后将复合熵转化为权重,权重计算公式为

(27)

归一化处理,得到权重

(28)

利用权重Wi,对BPA进行修正

(29)

(30)

2.3.2 加权求和与判决表达式

本文采用加权求和的方式代替Dempster融合公式,从而避免证据悖论问题,累加结果为

(31)

(32)

FC的判决表达式为

(33)

式中:λ是判决门限。

3 算法仿真与分析

本文仿真环境中,由一个PU信号、一个FC、10个SU组成协作频谱感知网络,网络模型参考于文献[22],SU随机分布在5 km×5 km的正方形区域中,FC位于该区域中心。本文以城市场景下的哈塔模型[23]作为路径损耗模型,其路径损耗标准公式为

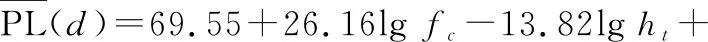
(34)

式中:fc为信号频谱;ht为发射机天线高度;hr为接收机天线高度;α(hr)移动天线高度的修正因子,本文选取移动天线高度修正因子为α(hr)=(1.1lgfc-0.7)hr-(1.56lgfc-0.8)。

本文仿真参数参考于文献[9],其中ht=100 m,hr=1 m,噪声功率为-106 dBm,对数正态阴影路径损耗模型方差σ和噪声方差σ0均为11.6,等效全向辐射功率为35 dBm,能量检测采样点数为512,蒙特卡罗仿真次数为10 000次。

假设10个SU中,分布着2～4个MU,MU根据其攻击目的不同,发动不同的SSDF攻击。本文算法和其他已有算法适用性如表1所示。

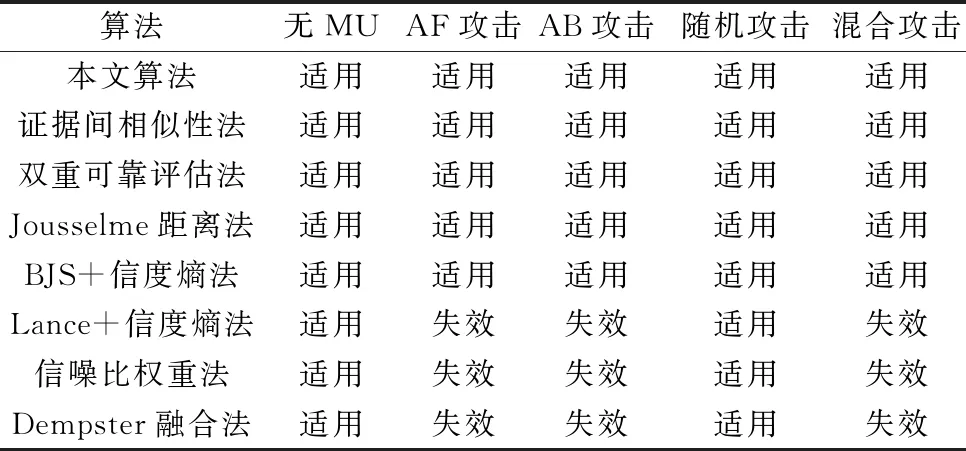
表1 仿真方案说明

相同虚警概率下,要求检测概率越大越好。因此,可以通过接收机工作特性(receiver operating characteristic,ROC)曲线,直观地比较不同算法的感知性能差异。

实验 1无MU时不同算法性能对比

无MU时,不同算法ROC对比曲线如图3所示。从图中可以看出,本文所提算法感知性能最佳,其次是证据间相似性法和信噪比权重法以及双重可靠评估法,这几种算法中,Jousselme距离法、Lance+信度熵法、BJS+信度熵法性感知性能接近,Dempster融合法感知性能最差。

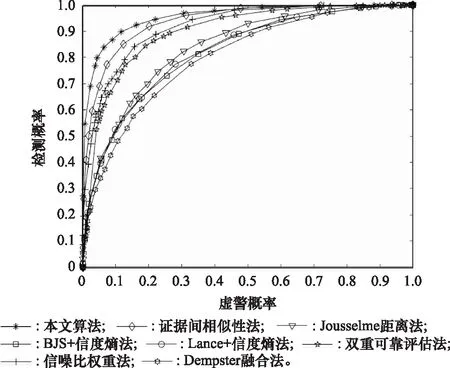
图3 无MU时不同算法ROC对比曲线

实验 2MU发动AF攻击时,不同算法性能对比

AF攻击时,不同算法ROC对比曲线如图4所示。由于Dempster融合公式的缺陷,MU发送篡改数据,导致信噪比权重法和Dempster融合法失效。Lance+信度熵法中,由于Lance距离公式的弊端,导致该算法失效。和无MU时的ROC性能相比,证据间相似性法感知性能下降最多,本文算法、双重可靠评估法和Jousselme距离法性能略有下降, BJS+信度熵法感知性能稳定。本文算法在AF攻击下,仍具有很好的感知性能。

图4 AF攻击时不同算法ROC对比曲线

实验 3MU发动AB攻击时,不同算法性能对比

AB攻击时,不同算法ROC对比曲线如图5所示。和AF攻击类似,MU发送篡改数据导致Lance+信度熵法,信噪比权重法和Dempster融合法失效。从图5中可以看出,和无MU时的ROC性能相比,证据间相似性法、双重可靠评估法、Jousselme距离法和BJS+信度熵法性能均有下降,本文算法性能稳定,且本文算法性能最佳。

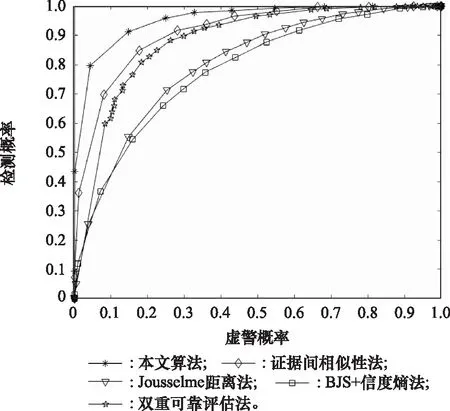
图5 AB攻击时不同算法ROC对比曲线

实验 4MU发动随机攻击时,不同算法性能对比

随机攻击时,不同算法ROC对比曲线如图6所示。从图中可以看出,和无MU时的ROC性能相比,Jousselme距离法和Lance+信度熵法感知性能基本保持不变,其他算法性能均有所下降。其中,Dempster融合法和BJS+信度熵法性能下降较小,本文算法和证据间相似性法性能下降较大,但本文算法具有最佳的感知性能。

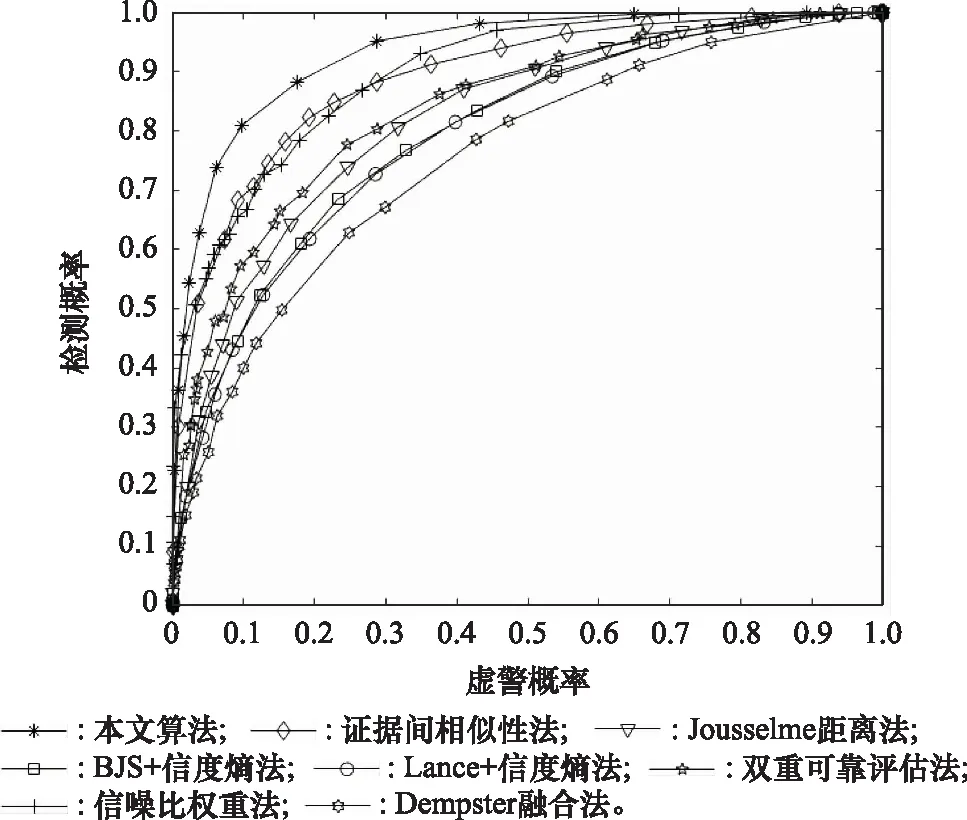
图6 随机攻击时不同算法ROC对比曲线

实验 5MU发动混合攻击时,不同算法性能对比

混合攻击时,不同算法ROC性能对比曲线如图7所示。由于混合攻击中,存在MU发动AF攻击和AB攻击,因此Lance+信度熵法、信噪比权重法和Dempster融合法均失效。在适用的5种方法中,只有Jousselme距离法感知性能基本不变,本文算法、双重可靠评估法、BJS+信度熵法和证据间相似性法感知性能均有所下降,但本文算法感知性能好于其他4种算法。

图7 混合攻击时不同算法ROC对比曲线

4 结 论

在基于证据理论的协作频谱感知中,针对SSDF攻击问题,本文提出了一种复合熵测度,通过对距离向量进行熵处理的方式,降低MU的权重,减小其对判决结果的影响。本地感知阶段,SU只计算对判决有用的信息,以减小信息计算量和传输量,同时根据感知信道的差异进行BPA调整。融合判决阶段,FC计算SU的复合熵,之后利用复合熵转化为SU的权重。针对Dempster融合公式的弊端,本文在信息融合阶段,用加权求和的方式代替Dempster融合准则。仿真结果表明,本文算法能够在MU发动不同类型的SSDF攻击时,保持稳定的感知性能。但本文所提算法适用于SU中,MU占比小于50%的场景,同时,在使用时存在损失部分本地感知信息的风险。此外,所提算法复杂度有所提升,研究高效抗SSDF攻击问题,这将是下一步有待解决的问题。