基于高斯混合过程的空间机器人任务空间预测控制方法

柳子然, 戴梓健, 岳程斐,*, 王培基, 曹喜滨

(1. 哈尔滨工业大学航天学院, 黑龙江 哈尔滨 150001;2. 哈尔滨工业大学(深圳)空间科学与应用技术研究院, 广东 深圳 518055)

0 引 言

近年来,人类探索宇宙、利用空间资源的脚步不断加快,提出了一系列长远计划,如空间太阳能电站[1]、深空轨道站[2]等,以空间机器人为代表的在轨服务航天器能够实现在轨制造、装配等功能,具有广阔的应用前景。但是,传统方法通常在关节空间中独立地进行规划和控制设计,不能直观地反映任务空间中的情况,难以胜任日益复杂的在轨操控需求。因此,直接在任务空间中进行控制器设计能够紧密围绕具体任务开展,日益受到重视[3]。

针对地面机器人的任务空间控制器设计已有广泛研究。文献[4]首先提出了操作空间控制(operation space control, OCS)方法,利用关节空间状态与任务空间状态的映射关系,将常用的关节空间机器人动力学方程转换到任务空间,再基于反馈线性化得到的线性模型设计了比例-微分(proportional derivative,PD)控制器并拓展到冗余机械臂中。Hogan等[5]则利用阻抗控制思想,设计了笛卡尔阻抗控制器,利用阻抗控制思想建立末端接触力与末端运动间的关系,并在任务空间设计控制器实现期望末端运动。近几年来,任务空间控制的研究逐渐扩展到漂浮基机器人中。Lippiello等[6]等推导了带有一条3自由度(degree of freedom, DOF)机械臂的无人机的动力学方程,并设计了笛卡尔阻抗控制器处理接触力和系统运动间的关系;Wang等[7]在任务空间中对双臂空间机器人的抓捕任务进行描述,并设计了滑模控制器以实现基座和末端对期望状态的精确跟踪。虽然以OCS为代表的任务空间控制策略不需要在位置层计算逆运动学,但是仍然需要在动力学转换阶段计算雅克比矩阵的逆及导数,在雅克比矩阵不确定或者不满秩的情况下难以直接应用[8]。此外,此类方法缺乏对空间机器人工作中可能遇到的约束的处理能力。

模型预测控制(model predictive control, MPC)在处理多约束优化控制问题上具有显著优势,因此在机器人、无人机等领域得到了成功的应用[9]。徐杨等[10]对无人车的路径规划和跟踪控制进行统一建模,利用MPC实现无人车辆的避障控制。在空间机器人方面,宗立军等[11]着重研究了自由漂浮空间机器人避障问题,将关节限制、避障要求统一描述为不等式约束,基于MPC提出了混合整数预测控制方法。同时,MPC也为解决机器人的任务空间控制问题提供了思路。针对机器人交互过程中的安全性约束,Nubert等[12]将传统分离的规划层和反馈控制层融合,设计了MPC器,在任务空间实现了机械臂末端对设定点的精确跟踪;Rybus等[13]设计了非线性MPC(nonlinear MPC, NMPC),实现了平面自由漂浮空间机器人对任务空间轨迹的直接跟踪;Shi等[14]对双臂空间机器人的任务空间动力学模型进行了线性化,并在此基础上设计MPC,实现了基座姿态与机械臂运动的协同控制。然而,作为一种基于模型的控制算法,MPC的控制精度与模型精度息息相关,同时MPC本身的计算量较大,必须尽量权衡模型精度和计算复杂度,以满足实时性要求。

高斯过程(Gaussian process,GP)回归作为一种常用的非参数化贝叶斯回归方法,需要求解的超参数较少,因此对样本数据量的需求较小,能够满足空间机器人、无人机等非线性系统在工作过程中的快速、精确建模需求,已被引入MPC框架并得到了成功应用。Torrente等[15]等利用GP对无人机运动过程中的高速风阻进行建模并部署到MPC控制器中,利用实验证明了GP-MPC的有效性;Woolfrey等[16]利用GP估计了运动基座对机械臂末端位姿的扰动,并利用MPC实现了末端对期望轨迹的跟踪。但随着样本维度和分布范围的增加,GP的计算复杂度显著上升[17]。为此,Leen等[18]提出了高斯混合模型(Gaussian mixture models, GMM),也称为高斯混合过程,通过对样本集分组且每组样本仅对应一个GP来降低每个GP的运算量,同时能够自动适应多模态的样本集。Liu等[19]利用GMM的思想训练得到了3DOF自由漂浮空间机器人模型;陈友东等[20]通过机械臂抓取实验演示了GMM相对于GP的优势。

针对空间机器人基座和末端对期望轨迹的直接、精确跟踪问题,考虑其工作过程中的模型不确定性和物理约束,本文提出了一种基于GMM和MPC(GMM-MPC)的空间机器人任务空间控制方法。与文献[13-14]等相比,考虑了基座受控的空间机器人在任务空间跟踪过程中受到的物理约束并利用NMPC进行优化求解;同时利用高斯混合过程对空间机器人的模型不确定性进行补偿和修正,相比于基于单GP(single GP, SGP)的GP-MPC进一步减轻了计算负担。

本文主要内容安排如下:在第1节中首先建立了空间机器人标称模型,并利用GMM进行修正,以应对实际工作过程中的模型不确定性;第2节将建立的空间机器人修正模型应用于MPC框架内,考虑了空间机器人基座的推力分配问题,实现了空间机器人任务空间的轨迹跟踪控制;第3节通过仿真验证了提出算法的有效性;最后在第4节对全文内容进行了总结。

1 基于GMM的空间机器人修正模型

1.1 空间机器人建模

本文研究所针对的空间机器人如图1所示,由单刚体卫星基座和n条刚性机械臂构成。为了方便描述空间机器人的位置和姿态,建立了以下坐标系:∑I为惯性系;∑B是空间机器人的基座系,原点位于基座质心,跟随基座运动;∑e1～∑en为第1～第n条臂的末端坐标系,以描述空间机器人在任务空间/笛卡尔空间的运动。此外,针对第m个关节定义有关节坐标系∑jm,以描述各机械臂在关节空间的运动情况。

图1 空间机器人示意图

对于配有n条机械臂,每条臂拥有m个自由度,平台配置L个喷气推力器的多臂航天器,给出其运动学和动力学的简要表述。

首先,根据机械臂末端与关节、基座状态的映射关系,得到空间机器人末端位姿的描述形式:

(1)

对位姿信息进行求导并整理得到空间机器人末端执行器的线速度和角速度、基座的线速度和角速度以及关节角速度之间的关系为

(2)

(3)

式中:JB为基座与各机械臂末端之间的雅克比矩阵;JM为空间机器人各臂与末端之间的雅克比矩阵。

在运动学模型的基础上,考虑基座受控情况下,关节空间中的机器人标称动力学方程:

(4)

式中:HB,HM,HBM分别为空间机器人基座惯量矩阵、机械臂连杆的惯量矩阵、基座与机械臂各连杆耦合惯量矩阵;CB,CM分别为基座和机械臂的非线性项;u0,uq分别为空间机器人基座和机械臂各关节作用的控制力和力矩。

整理得到状态空间表达式:

(5)

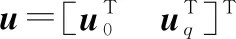
(6)

由此得到基座控制力和力矩与喷气推力器推力间的关系:

F0=CIBAT

(7)

式中:CIB为基座本体系到惯性系的转换矩阵;T=[T1,T2,…,TL]T为喷气推力器推力。

最后,为了便于将动力学模型应用在离散时间控制算法中,设定采样时间Δt,将连续的空间机器人动力学方程转化为离散时间模型,在当前k时刻测量值的基础上实现对未来k+N时刻系统状态的预测:

(8)

1.2 基于GMM的扰动估计方法

空间机器人在实际工作过程中,相比于标称模型,会受到如测量误差、关节摩擦等因素的影响,其实际动力学模型应为

Xk+1=Xk+δt·fnom(Xk,uk)+dk=ftrue(Xk,uk,δt)

(9)

式中:dk表示由于扰动产生的空间机器人干扰力矩。

为此,本文利用GMM对空间机器人所受干扰力矩进行估计补偿,如图2所示。

图2 基于GMM的扰动训练(左)和估计(右)方法示意图

GMM在GP的基础上,为了加快训练和预测速度,不再使用单一的GP假设,而是采用期望最大化(expectation-maximization, EM)算法对GMM模型进行训练,在训练样本聚类得到的M个子集基础上,对每个子集服从的高斯变量进行回归,最后在预测时,对各子集对应的局部预测值进行融合得到最终预测值。

GMM假设样本数据服从高斯混合分布,即包含A组样本数据的输入x,其概率密度分布函数为

(10)

式中:M为样本子集个数;πi为混合系数,代表样本来源于第i个高斯分量的概率;p(x|μi,Σi)代表由第i个高斯分量生成样本的概率;{μi,Σi}为高斯混合过程的超参数,其中μi代表均值向量,Σi代表协方差矩阵。

与GP的训练类似,GMM的训练过程即超参数{μi,Σi}和混合系数πi的求解过程。EM算法作为一种超参数求解的有效算法,核心思想类似最大似然估计或极大后验概率估计。主要过程分为两部分:期望步骤(expection-step,简称E步骤)和最大化步骤(maximization-step, 简称M步骤),两部分迭代进行。其中,E步骤利用M步骤估计的参数{πi,μi,Σi}计算第a个样本来自第i个高斯分量的后验概率ri:

(11)

M步骤通过E步骤计算得出的训练样本的后验概率ri,通过极大化对数似然函数更新模型参数:

(12)

其次,针对每一组高斯分量进行回归预测。扰动估计结果来自第i个高斯分量的后验概率为

(13)

(14)

式中:{xi,yi}是第i个高斯分量对应的训练数据;x*是测试数据;σy是量测噪声;Ki,K*i,K**i分别为训练数据之间、训练数据和预测数据之间以及预测数据之间的协方差,具体计算方式根据协方差函数,也称为核函数的形式确定。平方指数核是一种最常见的核函数,由于其连续可微而便于在NMPC过程中进行雅克比计算[17]:

(15)

式中:σf和l称为超参数,其求解一般通过最大似然估计实现:

(16)

(17)

2 基于MPC的任务空间控制方法

为了实现空间机器人在任务空间中的轨迹跟踪问题,同时应对实际工作过程中出现的驱动器输入饱和等约束以及模型失配,如图3所示,本文首先提出了基于GMM的NMPC,然后考虑了操作过程中空间机器人基座喷气推力器推力分配方法。

图3 GMM-MPC示意图

2.1 GMM-MPC设计

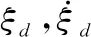
(18)

式中:Qr,Qt分别代表控制误差和输入惩罚项的加权矩阵;Xinit,ξinit分别为优化初始时刻采样得到的空间机器人关节空间和任务空间状态;umax,umin分别对应控制输入的上下限;N代表预测步数,通过对时域T进行离散化得到,即N=T/dt。

通过选择合适的控制器参数,包括Δt,N,Qr,Qt,求解上述优化控制问题,得到未来N个时刻的控制量U=[uk,uk+1,…,uk+N-1]T,仅将k时刻控制量uk作为系统输入。

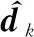
对于所提的MPC问题,考虑到计算量和实时性的要求,利用CasADi[22]和ACADOS[23]进行求解。其主要思路是首先利用多重打靶将其转化为非线性二次优化问题,再利用实时迭代策略下的序列二次规划进行求解。

2.2 基座推力分配方法

空间机器人基座运动所需的控制力和力矩由基座配置的喷气推力器产生。对于GMM-MPC求解得到的控制量uk,需要将其中基座的控制量u0分配并转化成对应激活推力器的控制指令。为此,本文构造了如下的优化问题以解决推力分配问题:

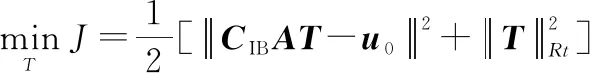
(19)

式中:Tlb,Tub代表推力器的推力饱和约束。

通过求解上述优化问题,得到了每个推力器的推力数值,在提供基座控制需求的同时,满足能量消耗最少和推力饱和约束。但是,求解得到的是在[Tlb,Tub]间的任意大小的值,而常用的星载冷气推进器一般只能提供最大推力与零推力两种模式。因此,为了满足实际推力器的“开-关”控制模式,通过脉冲宽度调制(pulse-width modulation,PWM)方法将连续推力转换为每个推力器开机时间:

(20)

最后,考虑推力器的最小开机时间Δtc,得到最终的推力器驱动指令:

(21)

3 仿真校验

3.1 仿真模型构型及参数

首先,介绍仿真所用的空间机器人系统构型及参数。考虑到三维多臂机器人系统自由度较高,应用所提出算法求解复杂,同时为了后续在实验室已有硬件基础上进行实验,本文以一个平面空间机器人模型进行仿真,着重验证算法的有效性而避免对计算量的讨论。其仿真构型如图4所示。

空间机器人模型每个连杆的质心位于连杆的中心处;惯性系初始时刻与机器人基座系重合,其惯性参数如表1所示。由于仅考虑空间机器人的平面运动,因此提供驱动的8个喷气推力器沿xB-yB平面布置,即γl=0,∀l=1,2,…,8,具体的推力器构型参数见表2,其中[xTl,yTl]T代表推力器安装位置,βl代表指向角度。

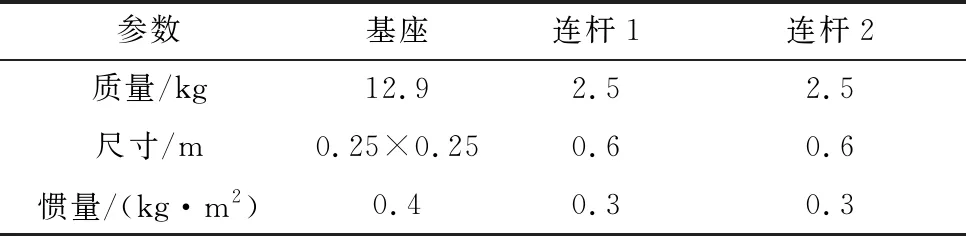
表1 空间机器人惯性参数

表2 推力器构型参数

3.2 仿真场景设置

为了验证本文提出算法的有效性,给定空间机器人初始状态ξ0=[0,0,0,0,0,0]T,跟踪参考轨迹为

(22)

式中:tn=t/tf,tf代表期望运动时间;ξ1,ξf分别为期望轨迹的起始状态和末状态。

同时,在轨迹跟踪的过程中,为了让仿真结果尽可能地贴合现实情况,参考文献[17,24]引入两种形式的模型不确定性:第1种由连杆长度、质量、转动惯量等参数误差产生,但本文中并非一一对其进行考虑,而是将其集总为中模型参数的偏差,即将H和C与真值的相对误差设置为30%;第2种为周期性扰动:

(23)

3.3 仿真结果

为了实现第3.2节中描述的仿真任务场景,设计了GMM-MPC控制器进行仿真研究,并将仿真结果与标准MPC控制器以及SGP结果进行对比,验证本文设计方法的有效性和优越性,仿真所用参数见表3。

表3 仿真参数

在仿真开始之前,利用标准MPC控制器跟踪一系列期望轨迹,建立包含1 400组[x,y]的数据集,其中1 300组用于训练得到GMM,100组用于进行模型的性能测试。训练和测试结果如图5～图7所示。其中图5(a)和图5(b)分别描述了训练得到的高斯混合模型在测试集上的一步预测结果,可以看出GMM能够有效地估计扰动对于空间机器人基座和关节的影响,即使对于基座角度和轻质关节处产生的大幅变动也有较好的估计效果。为了量化并对比GMM估计结果,计算了均方根误差(root mean square error, RMSE):

图5 GMM测试结果

(24)

为了避免偶然性,计算得到5次预测的平均RMSE为[0.014 6,0.001 9,0.054 9,0.068 0,0.087 5]。图6进一步说明了训练样本数量与估计结果,即平均RMSE的关系,可以看出训练样本过少时估计效果较差,提供更多的训练样本可以尽可能地提高精度,但是训练和预测过程将更加漫长。因此在500～600左右可以实现理想的精度,同时不消耗过多计算资源。最后比较了GMM与SGP的估计结果,如图7所示,可以看出相同样本数量情况下GMM比SGP精度有着明显改善。随着样本数量的提升,SGP精度提升明显。

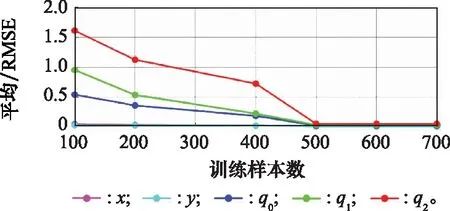
图6 GMM估计结果与训练样本间的关系

图7 GMM与SGP结果对比

最后,针对空间机器人的期望轨迹跟踪问题,分别设计了基于标准MPC和部署了训练得到的GMM的GMM-MPC进行实时仿真,以验证提出方法的有效性,仿真结果如图8所示。对于没有进行不确定性补偿的标准MPC控制器,其预测使用的标称动力学模型与实际动力学模型存在明显差异,导致预测时域内的系统状态估计值与实际值不符,进而影响控制信号求解。由于MPC本身具有一定的鲁棒性,因此虽然图11中所示的标准MPC跟踪误差仍存在收敛趋势,但在30 s时依然出现震荡,收敛时间长,控制性能较差。

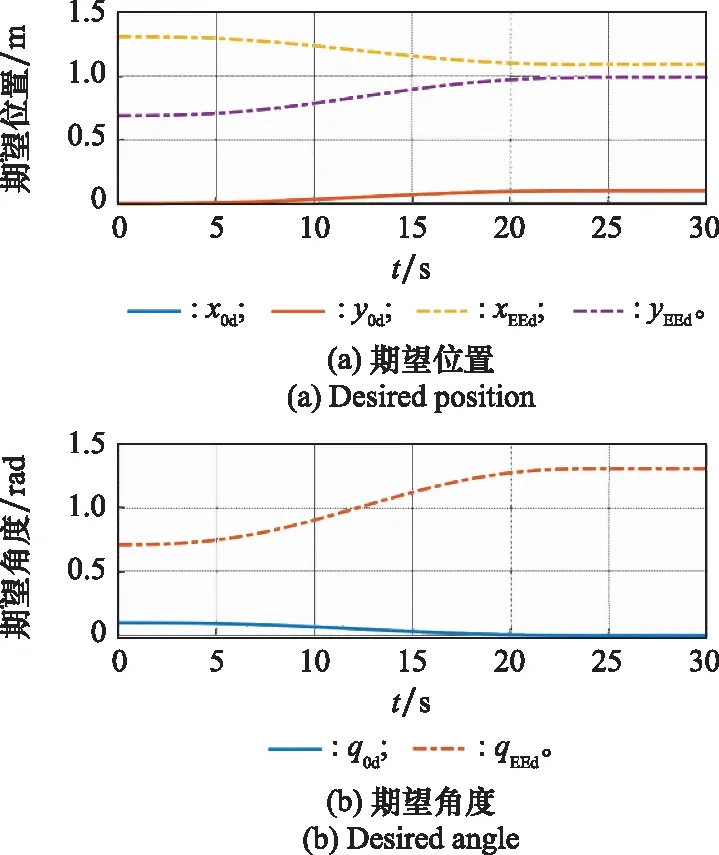
图8 空间机器人期望轨迹

而GMM作为一种有效的数据驱动非线性系统建模方法,能够对模型不确定性进行较为精确的补偿。由图9和图10可以看出,基于GMM-MPC的空间机器人控制器在5 s以内控制误差即收敛到0,与如图11所示的标准MPC跟踪情况相比,有了明显的改善,特别是针对末端状态的控制,由于扰动累积和基座/机械臂质量比的影响,末端处模型不确定性较大,在标准MPC控制器作用下,相较于基座控制性能更差,但在GMM-MPC作用下其性能得到了有效提升。

图9 GMM-MPC跟踪结果

图10 GMM-MPC跟踪误差

图11 标准MPC跟踪误差

但同时可以注意到,图9、图10所示的跟踪结果相比期望轨迹仍然存在一些偏差,这一方面是由于喷气推力器存在死区特性,更主要的原因在于GP,包括GMM,其长期预测能力有限,因此在测试集上估计效果较好,但是在仿真应用中,随着MPC预测时域的增长,GP的估计精度会有所下滑[19]。

整个任务过程中的推力器激活情况如图12、图13所示,初始阶段由于轨迹跟踪误差较大,部分推力器激活时间较长。由于需要抑制模型不确定性和机械臂运动的影响,以及推力器存在死区特性,随着跟踪误差逐渐收敛,推力器激活时间减短,但不会完全关闭。

图12 推力器T1-T4启动情况

图13 推力器T5-T8启动情况

4 结 论

本文针对空间机器人的任务空间轨迹跟踪控制问题,提出了一种基于高斯混合过程的MPC方法。首先,利用MPC解决了空间机器人基座和末端位姿对设定点的直接跟踪,同时满足输入饱和等实际物理约束。为了解决预测过程中由于模型不确定性带来的干扰,利用预实验数据训练得到高斯混合过程以估计标称动力学的误差,并部署到MPC框架中。最后,考虑到空间机器人基座的驱动形式,设计了喷气推力器的推力分配方法。仿真结果表明,相比于SGP,GMM需要样本更少、预测效果更好,本文提出的基于高斯混合过程的MPC方法能够有效地实现空间机器人对任务空间参考轨迹的跟踪,保证任务成功完成的同时更加直观、简便。