基于随机服务系统的海上要地防空体系目标信息处理模型

赵文飞,王 ,*,滕克难, 陈 健, 周 璐

(1. 海军航空大学, 山东 烟台 264001; 2. 中国人民解放军92199部队, 山东 青岛 266000)

0 引 言

海上要地面临的空中威胁复杂多变,空袭手段呈现愈加多样化、综合化、一体化和系统化的特点[1-3]。当有空中目标来袭时,快速地处理来袭目标的信息、准确地做出目标威胁评估(target threat assessment, TTA)是取得海上要地防空作战的关键[4-6]。因此,在构建要地防空体系指挥通信系统时,需要尽可能地缩短目标信息在各参战单元间的传递时间,提高信息处理效率。

关于作战体系的TTA问题已有许多学者进行了深入的研究,杜继永等[7]针对防空系统评估指标信息的不确定性和模糊性,利用模糊层次分析法分配各指标的权重,并给出了数学模型和操作方法。付涛等[8]提出了一种将空中目标威胁因子分为定量指标和定性指标的新的防空系统中评估目标威胁度方法,并通过贝叶斯网络进行推理以得到静态威胁值。李一夫等[9]针对联合防空任务下舰艇编队威胁评估问题,提出了一种立足体系作战、以装备体系贡献度为依据的威胁评估方法,综合运用复杂网络理论和熵权-灰色关联法、云模型理论等效能评估方法,从结构贡献和能力贡献两个维度解构装备在作战体系中对遂行作战任务的体系综合贡献程度,并根据体系贡献度进行威胁评估。

上述学者虽然对防空作战体系威胁评估问题从不同角度采用多种理论进行了研究,但对该问题中来袭目标信息的处理过程均没有进行深入探讨和定量分析。众所周知,对来袭目标信息快速准确地处理是进行TTA的前提,海上要地防空作战由于其地理位置的特殊性,战略纵深小、预警时间短,整个作战过程需要争分夺秒,因此亟需构建灵活精准的来袭目标信息处理网络来满足作战要求[10-11]。本文针对以上问题,采用随机服务系统理论对海上要地防空体系中的目标信息传递处理过程进行数学模型构建,对整个目标信息处理过程进行研究。第1节对目标信息处理过程对威胁评估的影响进行分析,第2节主要介绍数学模型的构建思路,第3节采用构建的模型对算例进行仿真与实验分析,第4节为结论与展望。

1 问题描述

在研究海上要地防空体系威胁评估过程时,需要考虑目标信息处理效率的因素,因为防空作战时需要防空体系在最短的时间内最大限度地处理来袭目标信息,以保证后续威胁评估、火力分配等作战过程顺利进行[12-15]。在实际海上要地防空作战过程中,由于参战装备有限、作战准备时间较短等因素,防空体系内的各参战单元需要在指挥通信网络的组织领导下构成一个有机整体,以最大限度地发挥各参战单元的作战效能。

目前,对于指挥通信网络的架构有两种模式,分别是以平台为中心和以网络为中心。这两种体系的主要差别在于目标信息在体系中的传递形式:在以平台为中心的防空体系中,目标信息会严格遵照体系中规定的指挥层级,按照由各参战单元到指挥所的路径进行传递,因此不同参战平台获取信息的权限不同,得到的目标信息准确性、完整性、实时性等也不尽相同;在以网络为中心防空体系中,目标信息可以在任意两个作战单元直接自由传递而不受指挥控制层级限制[16]。以网络为中心的作战体系意味着各参战单元及通信网络,构成一个互联互通的网络,实现侦察预警单元、信息处理单元、指挥机构以及火力打击单元的互相串联。这种以网络为中心的指挥控制网络能够像所有要地防空作战单元提供更为准确、完整、实时的来袭目标信息[17-19]。

现今已有许多国家提出类似概念并进行研究、部署,如美国的网络中心战概念、英国的网络启用能力概念、荷兰的网络中心作战概念、瑞典的网络防御概念以及北约国家的北约网络启用能力概念等。近几年,我国提出了综合网络电子战概念,并朝着这个方向进行军事理论研究与装备技术研发[20-21]。

由于已有的针对要地防空体系指挥通信网络的架构的研究,主要均从理论层面定性地分析两种模式的优劣,本文考虑基于随机服务系统理论构建防空体系指挥通信体系模型,并对哪种架构模式更能满足实际作战需求进行研究。

2 模型构建

在海上要地防空过程中,将防空体系中的指挥通信系统视为“服务机构”,来袭目标信息视为“顾客”,当来袭目标信息超出服务能力后,目标信息则不再等待,视为放弃服务,记做指控系统不能即时处理目标信息,即系统丢失目标特征信息。由于指挥单元的相互关系对整个网络的构成影响较大,因此将各指挥单元在海上要地防空体系中的关联类型作为本文模型的输入参数[22-23]。在以网络为中心的要地防空作战体系中,各单通道随机服务系统中的目标信息请求流(目标信息流)被均匀合并成一个整体的随机服务系统,如图1所示。

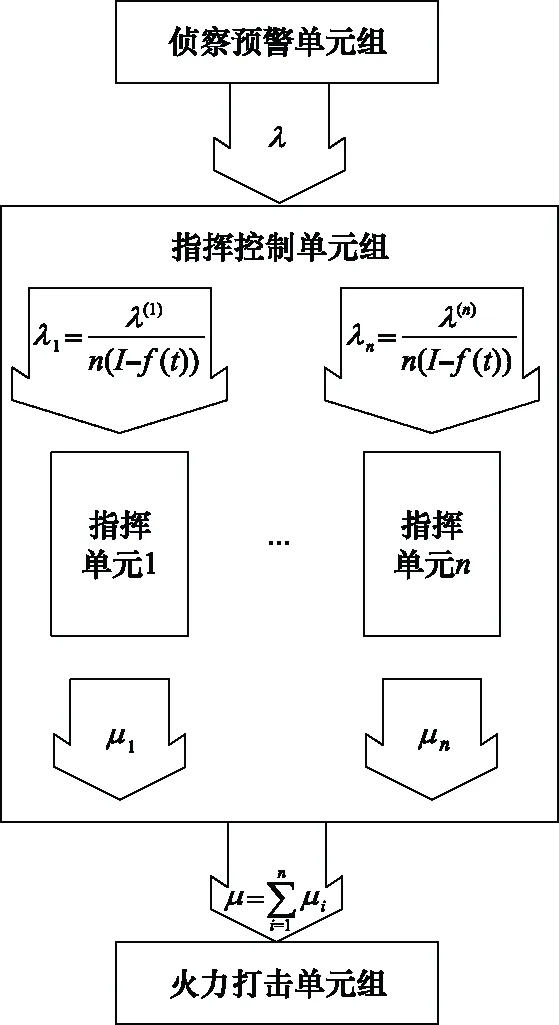
图1 以网络为中心的防空体系单元关系

图1中,λ(1),λ(2),…,λ(n)分别是通道1,2,…,n的目标信息请求强度,表示将目标信息请求重新分配到另一个指挥单元的可能性,这是以网络为中心的作战系统的一个显著特征,将其与以平台为中心的系统区分开来。

随机服务系统的功能可表述如下,该系统由n个公共通道组成。在某些因素的影响下,通道的数量会减少,主要是敌方火力打击、电子压制等因素影响。设平均强度为λ的最简单请求流进入系统;服务请求形成每个信道强度为μ的输出流;队列长度l,即队列中的请求数已明确[24-26]。从队列中驱逐请求的平均强度ν等于单位时间内的请求数。系统在特定时间t发生信道故障,故障率设为函数f(t)[27-28],一般情况下,函数f(t)可设为(0,1)区间的随机数。图1显示了以网络为中心的单个作战单元关联的具体情况,其中通道数量的增加意味着到达强度的成比例降低。对于以平台为中心的关联,强度可能因渠道而异。因此,为了概括侦察信息的处理和分布,对每个信道保持不同到达强度的可能性。

由于指挥单元间的关联非常重要,因此指挥单元层次结构中的关联类型是模型的输入参数。系统从一种状态到另一种状态的转换会受到3种不同事件流的影响:到达服务的请求流λ;强度为μ的服务请求流;和强度为lv的请求流,离开队列(系统)而不被服务。以网络为中心的随机服务系统可被视为信道数为n(1-f(t))的多信道排队系统。因此,指挥单元的集合是有限等待时间和无限数量队列的多通道随机服务系统。在本文中,多通道系统意味着以网络为中心的随机服务系统,而单通道系统对应于以平台为中心的随机服务系统。

以网络为中心的随机服务系统具有以下状态,Sj状态对应于系统中的j请求。当请求数小于公共通道数,即j≤n时,没有出现排队情况;当j>n时,所有通道都忙,且j-n处于队列中。随机服务系统中的过程是马尔可夫链,其主要属性是无记忆性,也遵循“死亡和传播”的过程,因为所有的流都是简单的,并且以相反的方向把系统从一个状态带到另一个状态,系统的状态如图2所示。为了简化模型,引入了以下符号:ρ=λ/μ是平均服务时间内请求流到达强度;ϑ=v/μ是指因超过等待时间,系统中排队的请求流未接收服务的强度。

图2 以网络为中心的随机服务系统等待时间有限时多通道示意图

系统可能的状态描述如下:

S0:n个通道空闲,系统内有0个请求流;

S1:1个通道繁忙,系统内有1个请求流;

⋮

Sn:n个通道繁忙,系统内有n个请求流;

Sn+1:所有通道繁忙,系统内有1个请求流等待被服务;

⋮

Sn+l:所有通道繁忙,系统内有l个请求流等待被服务。

根据平衡状态原理,可得方程组:

从而可得

(1)

其中,归一化条件为

p0+p1+p2+…+pn+…+pn+l=1

(2)

将式(1)代入式(2)可解得

(3)

当目标信息在系统停留时间较短,系统来不及腾出通道对其进行服务,则意味着目标信息不被服务,假设系统中平均有s个目标信息等待被服务,则目标信息不被服务的概率为

(4)

在以平台为中心的关联情况下,随机服务系统中的n个通道可视为向n个不同的方向独立地提供目标信息服务,每个通道服务情况如图3所示。

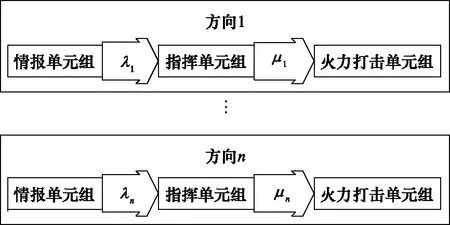
图3 以平台为中心的随机服务系统作战单元子系统

在以平台为中心的要地防空体系中,指挥单元具有有限的等待时间和无限数量的队列可视为多个单通道随机服务系统的组合,系统状态为Sj+k,其中j∈{0,1},S0表示系统中没有目标信息,当j=1时,Sj+k表示系统中有k个目标信息在队列中等待服务。系统的状态图如图4所示。

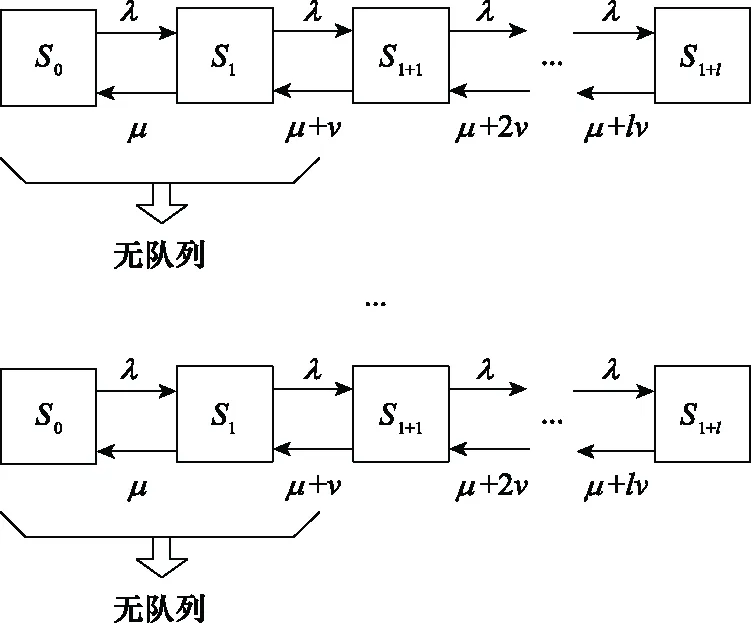
图4 具有有限等待时间的单通道随机服务系统关联状态示意图

类似以网络为中心随机服务系统状态概率的求解方法,可得到单目标通道随机服务系统的状态概率方程组:

(5)

因此,所有通道空闲的概率,即不存在队列(对于单个通道)的概率为

(6)

因此,目标信息不被服务的概率为

(7)

在以平台为中心的互联情况下,假设每个单目标通道参数是一致的,则只需要对其中一个通道的服务情况进行分析,而不需要对所有通道进行评估。综上所述,以随机服务系统理论为基础的决策模型如图5所示。

图5 决策管理的随机服务系统理论框图

3 算例仿真

为了比较两种类型体系信息交互的有效性和模型对输入参数的敏感性,使用式(5)和式(8),即分别以网络为中心和以平台为中心的模型,在不同通道数n、不同目标信息申请流强度λ和不同的ρ情况下计算拒绝处理请求的概率pref。

仿真算例1在不同通道数n、目标信息申请流强度λ的情况下,分析以平台为中心和以网络为中心的来袭目标信息处理体系中的pref。

假设目标信息申请流λ分别为100,200,300次/小时,μ=50次/小时,通道数n={1,2,…,10},v=10次/小时,l=5次,f(t)=0.5。根据上述数据,利用Matlab编程仿真结果如图6所示。

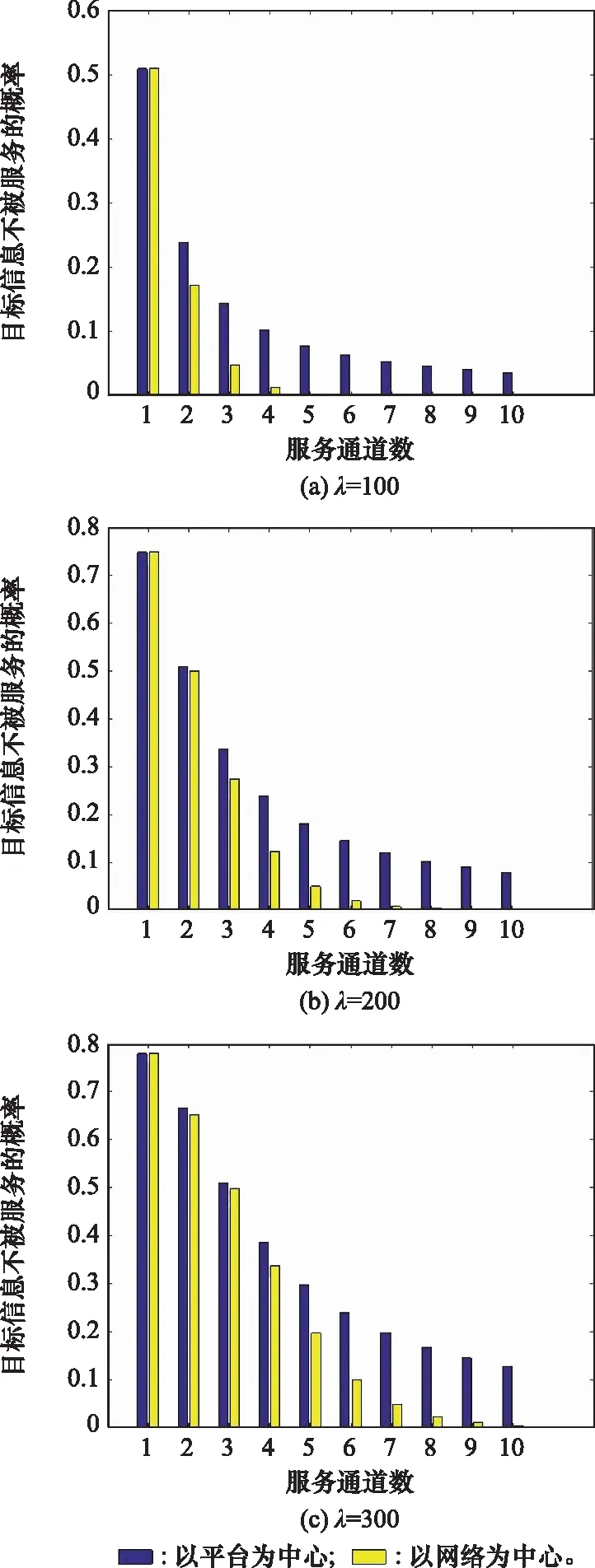
图6 两种体系在不同通道数下的pref

从仿真结果不难得到以下几个结论。

(1) 在相同情况下,以网络为中心的目标信息处理系统的pref较低。

(2) 当通道数较少、目标信息申请流强度较大时,以平台为中心和以网络为中心的目标信息处理系统pref差别不大。从图6(c)可明显得出,当λ=300次/小时,通道数小于5时,两类平台的pref差距不大。主要原因是系统超负荷运载,服务强度远满足不了信息申请流的服务请求。

(3) 当通道数较多时,相比以平台为中心,以网络为中心的目标信息处理系统pref优势非常明显。但是,当通道数多到一定程度,各通道需要服务的请求较低时,两类系统的差距又将进一步缩小。

仿真算例2:在通道数n=5,7,λ=200次/小时,v=10次/小时,l=5次,f(t)=0.5的情况下,分析以平台为中心和以网络为中心目标信息处理系统的pref与平均服务时间内信息申请流强度ρ的关系。仿真结果如图7所示。

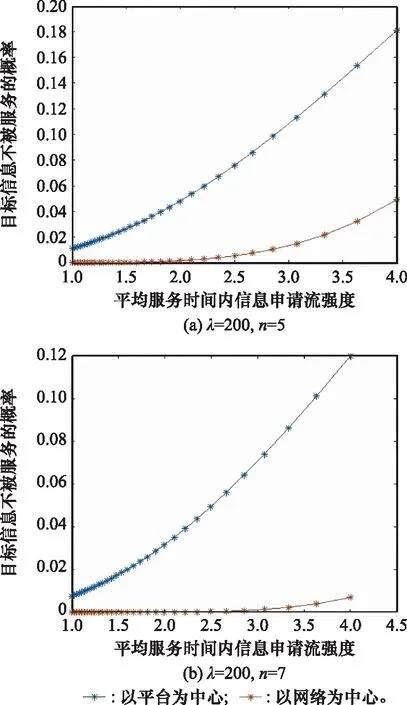
图7 不同来袭目标信息强度下两种体系拒绝概率

从仿真结果可以看出,以网络为中心目标信息处理系统pref明显低于以平台为中心的情况,尤其是在平均服务时间信息申请流强度较大,系统中负荷比较重时,以网络为中心的目标信息处理系统优势十分明显。在通道数n=5, 负荷ρ=4时,以网络为中心的目标信息处理系统pref=0.056,以平台为中心的目标信息处理系统pref达到了0.185;而在通道数n=7, 负荷ρ=4时,以网络为中心的目标信息处理系统pref,只有0.007,以平台为中心的目标信息处理系统pref=0.12,再次表明以网络为中心的系统服务效率更高。

4 结 论

本文就海上要地防空体系来袭目标信息处理过程难以量化的问题,提出了一种能够适用于防空体系信息处理过程研究的随机服务系统理论模型,其主要优点如下。

(1) 分别考虑以平台为中心和以网络为中心的海上要地防空体系来袭目标信息处理过程的特点,构建不同随机服务系统模型,能够合理模拟不同网络结构下来袭目标信息处理过程。

(2) 通过构建随机服务系统模型,将不同体制下来袭目标信息处理过程模型化、数字化,克服了以往在研究体系威胁评估过程时只能定性分析的问题。

(3) 针对不同的防空体系以及战场环境,可以通过调整模型相关参数来对来袭目标信息处理过程进行仿真分析,构建的模型具有一定的普适性及实用价值。

综上所述,本文提出的基于随机服务系统模型能够较好地模拟海上要地防空体系来袭目标信息处理过程,为研究防空体系目标信息处理过程提供了一种有一定应用价值的新方法。