基于MLS的三维扩展目标PMBM跟踪算法

衡博文, 李翠芸, 李 想

(西安电子科技大学电子工程学院, 陕西 西安 710071)

0 引 言

目标跟踪是根据传感器获得的数据,对一定观测区域内运动目标的状态进行估计的过程。扩展目标跟踪除了跟踪目标运动状态外,还要估计目标的形状。基于随机有限集[1]理论的目标跟踪方法避免了复杂的关联计算,关联精度也更高。其中,泊松多伯努利混合(Poisson multi-Bernoulli mixture, PMBM)滤波器[2-3]使用泊松点过程表示未检测到的目标,即使在目标存在漏检、新生或消亡的情况下,依然能够准确估计多目标的状态,因此一经提出就成为了研究热点。现有的扩展目标形状估计方法大多是针对二维目标的。其中,较为典型的是随机矩阵(random matrices, RM)[4]和随机超曲面模型(random hypersurface model, RHM)[5],而B样条[6-7]和高斯过程[8-9]也常用于扩展目标跟踪。文献[10]将RHM和伯努利滤波算法相结合,实现了对椭圆扩展目标的跟踪。除此之外,Lan等人针对非椭圆目标提出了多椭圆法[11-13]。随后,文献[14]针对多椭圆法做出了改进,不需要预先设定子椭圆数量且子对象数量可变。

在三维目标的形状估计方面,文献[15]将Karl等人提出的伽马高斯逆威舍特PMBM(Gamma Gaussian inverse-Wishart PMBM, GGIW-PMBM)滤波器[16]扩展到三维空间,但只能将目标建模为椭球,不能对目标形状进行精细刻画。文献[17]通过径向函数和高斯过程来估计目标三维形状,但三维点云数据的计算负载较高。文献[18]将稀疏点云测量与高斯过程结合来估计三维目标表面,但计算量大、估计精度不高。利用B样条对三维目标的形状进行估计时,需要对样条曲线进行拟合,再由拟合后的B样条曲线组成B样条曲面。这种方法估计出的目标三维形状平滑,但每次估计形状时都需要进行曲线的拟合,计算量较大、算法运行时间长。

针对以上问题,本文提出了一种基于移动最小二乘(moving least square, MLS)模型的扩展目标MLS-PMBM滤波跟踪算法。算法将融合后的量测集输入至PMBM滤波器,获得目标质心运动状态,通过MLS模型处理量测数据,对形状矩阵中的控制点进行移动,结合目标质心状态与形状估计完成对三维扩展目标的跟踪。仿真实验与实际点云数据的验证表明,本文所提算法在三维目标形状估计方面具有更高的精度,在实际场景中能够实现对不规则形状扩展目标的有效跟踪,泛用性更广。

1 扩展目标跟踪模型

文献[19]中的MLS算法[20]通过调整控制点,可将简单形状变形为复杂目标的形状,并且简单形状可以预先设定,控制点则根据量测数据进行计算。该理论可在三维空间中对扩展目标的形状进行估计。

1.1 MLS算法

MLS算法引入了紧支撑权函数,保证了在目标跟踪中单个量测的影响区域有限。紧支(compact support, CS)即函数值y只受x附近邻域内数据点的影响,域内定义x的权值函数为ω(x)。在拟合区域上,待拟合函数可表示为

f(x)=μ(x)×p(x)

(1)

式中:μ(x)=[μ1(x),μ2(x),…,μm(x)]T是系数向量;p(x)=[p1(x),p2(x),…,pm(x)]T是基函数;m是基函数的项数,基函数有线性基、二次基和立方基。由拟合函数和y利用加权最小二乘算法得到

(2)

式中:n是x邻域内的数据点数量;ωi(x)是节点x的权函数。在节点x的邻域内,ωi(x)>0;在邻域外,ωi(x)=0。将式(2)转为矩阵形式,并对μ(x)求偏导得

J=(Pμ-y)TW(Pμ-y)

(3)

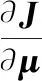
(4)

其中

y=[y1,y2,…,ym]T,μ(x)=A-1(x)B(x)y

(5)

A=DTW(x)D

(6)

B=DTW(x)

(7)

其中

(8)

(9)

将式(4)代入式(1)可得拟合函数为

(10)

其中

Φ(x)=[φ1(x),φ2(x),…,φm(x)]=p(x)A-1(x)B(x)

(11)

基于最小二乘算法的图像变形,最早于2006年由Schaefer等提出[19]。当利用MLS算法处理要变形的图像时,可以将变形后的图像中的点视为变形前图像中的点的映射,这种映射变换设为函数f。为了便于描述,在此设p为变形前图像点集,q为点集p经过f变换后的变形后点集。利用MLS算法构造的变换f可满足性质[21]。设点v为变换前点集p中的一个点,为了求得最佳变形函数lv(x),需得满足式(12)取最小值:

(12)

式中:p和q分别是变形前和变形后的控制点集;wi为权重值;pi指点集p中的第i个控制点;每个控制点都有对应的权值函数和变形函数lv。上文提到的变换f是对变形函数lv的抽象表达,即f(x)=lv(x)。

1.2 形状矩阵模型

在多目标跟踪中,三维扩展目标的形状可以看作是由简单形状变形而来,变形前的形状称为初始形状,通常选取球体作为初始形状。如图1所示,在给定初始形状的曲面上设立控制点,控制点组成的矩阵即形状矩阵C。形状矩阵随时间进行估计和更新,当前时刻更新后的形状矩阵在下一时刻将再次进行估计。

图1 初始化形状与控制点

形状矩阵中的每一个元素代表扩展形状上的一个控制点,在三维空间中,可以用一组三维坐标表示控制点的空间位置。首先对扩展形状进行空间上的划分,在z轴方向上划分a个区域,对于每个区域,在水平方向上沿顺时针方向再划分b个子空间。在每个子空间中设置一个控制点,通过划分到该子空间范围内的量测对控制点进行更新。

参数a和b决定了子空间的数量,子空间越多,对应的控制点就越多,需要的量测也越多。选择合适的参数对于形状矩阵的精确性十分重要,a和b过小会导致控制点过少,从而无法准确描述目标外形;过大则会导致子空间过小,如果小于传感器的距离分辨力,就无法获得有效量测。设Δd为传感器的距离分辨力,则子空间参数应满足以下条件,即

(13)

式中:r为初始形状的半径。

2 基于MLS模型的PMBM滤波算法

在多扩展目标的跟踪中,主要是对3部分状态进行估计,分别是扩展目标的量测率、运动学状态和扩展形状。通过3个分布分别表示上述状态,并建模为

x=(xR,xC,xε)∈R+×Rn×Sm

(14)

式中:xR∈R+、xC∈Rn和xε∈Sm分别表示目标产生量测的泊松率、目标的运动状态和目标的扩展状态,其中扩展状态由MLS模型进行建模;R+、Rn和Sm分别为正实数空间、n维实数空间和m维状态空间,且m=a×b。所以,目标在时刻k的状态是上面3个状态的乘积,即

(15)

(16)

(17)

式中:Δqk表示控制矩阵中控制点变换前后的偏移量均值;σk是控制点偏移方差。将上文提出的模型与PMBM滤波器相结合,给出滤波过程:

步骤 1状态初始化并获得量测集

首先,根据PMBM滤波器中的PPP模型对目标进行初始化,目标量测率与运动学状态均与PMBM滤波器相同[16]。根据形状矩阵模型建立形状矩阵C。C中的控制点在变换的过程中,只受邻域内量测数据的影响。实验中选取的是均匀控制点,将目标沿z轴方向的长度与水平方向的旋转角按照a和b进行等分,每个区域的中心即为设立的控制点。需要注意的是,控制点之间的距离理论上要不小于每个控制点的邻域半径ε,否则可能会出现控制点错位的现象。在MLS模型中,一个量测点可能处于多个节点的邻域内,这就意味着这个量测数据可以用来求解多个控制点变换后的位置。

步骤 2预测

进行预测时,目标的强度由伽马高斯MLS(Gamma Gaus-sian MLS, GGM)联合分布来表示。其中伽马分布用来表示量测率,高斯分布表示目标的运动学状态,M分布实际服从高斯分布,这里指基于MLS模型的三维目标的扩展形状。目标状态可参数化表示为{α,β,m,P,M,Σ},目标的强度为

从客观的角度来分析，公路施工期噪声的出现，是多种原因共同造成的，而且在处理的难度上较高，必须坚持长久监测，并且落实多元化的防治手段。与此同时，公路施工期噪声的应对过程中，应加强不同影响因素的科学应对，这样才能在未来工作的实施过程中，不断的取得更好的成绩。有些地方的公路施工期噪声监测，由于没有在体系上达到健全状态，由此造成的损失是持续性的，应保持高度关注，并且在借鉴力度上不断的巩固。

(18)

(19)

(20)

式中:j表示第j个多伯努利(multi-Bernoulli, MB)项;i表示该MB项中第i个伯努利项。

目标量测率和运动学状态的预测见文献[17],这里只对目标的扩展形状的预测进行说明,预测步骤如下:

M+=FsM

(21)

Σ+=FsΣ(Fs)T+Qs

(22)

其中,

(23)

步骤 3更新

没有关联到量测时的扩展状态由于没有量测进行更新,所以维持原状:

Mk|k=Mk|k-1,Σk|k=Σk|k-1

(24)

当目标关联到量测时,设量测集为W={z(1),z(2),…,z(|W|)},则量测率的更新为

αk|k=αk|k-1+|W|,βk|k=βk|k-1+1

(25)

目标运动学状态更新为

(26)

Pk|k=Pk|k-1-KkHPk|k-1

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

式中:Hl的含义见文献[21]。最后,根据更新后的状态并结合MATLAB中的曲面拟合函数,得到三维空间中目标的扩展形状。

3 仿真实验与分析

为了验证所提算法在目标三维形状估计方面的有效性,本节设计实验对比了GGIW-PMBM和MLS-PMBM滤波算法在三维形状估计方面的性能。此外,利用SYDNEY URBAN OBJECT公开数据集的点云数据生成模拟量测,验证了MLS-PMBM在街道场景中的实际跟踪效果。实验中的量测均为表面量测,共设置了两组实验,实验1对比多目标场景下,估计多种扩展目标形状时两种算法的有效性。实验2模拟复杂情况下的真实场景,验证MLS-PMBM的工程应用价值。蒙特卡罗次数为100,本文采用的评价指标有两个,对于目标质心运动性能的评价,采用的是最优子模式分配距离(optimal sub-pattern assignment,OSPA)[16];对于目标形状的估计,采用的是交并比(intersection-over-union,IoU)[22],即估计结果与真实值交集和并集的比值,该值越接近1,表示估计结果越贴合实际。

实验 1为了研究MLS-PMBM和GGIW-PMBM同时对多个扩展目标的跟踪能力,设置如下实验场景。算法跟踪区域为[-200,200]m×[-200,200]m×[-200,200]m,传感器的位置分别为[250,-200,250]m、[-200,250,250]m和[-250,-250,-250]m。目前,激光雷达输出的点云数据大多包含有方位角和三维笛卡尔坐标等空间位置信息,可以直接作为MLS-PMBM的输入,因此传感器均假设为同型激光雷达;初始化的扩展目标形状是球体,球径为3 m。其中目标1是轴长分别为2 m、2 m和1 m的椭球;目标2是边长为4 m的立方体;目标3为十字架,长为10 m,宽为8 m,高为2 m,目标的体积差异不影响本文算法的形状辨识性能。扩展目标的运动学模型为CV模型,其状态转移矩阵F,量测矩阵H,过程噪声协方差矩阵Q和量测噪声协方差矩阵R为

(36)

(37)

图2是全局坐标系下所有传感器的量测,图中3个目标的运动轨迹并没有在运动过程中相交。图3是3个目标的运动轨迹。表1说明了目标的初始化状态与存活时间。图4～图9是两种算法跟踪椭球目标、立方体目标和十字架目标的局部放大图。

表1 目标的初始化参数

图2 跟踪多个目标时传感器接收到的量测

图3 3个目标的运动轨迹

图4 MLS-PMBM估计椭球目标形状效果图

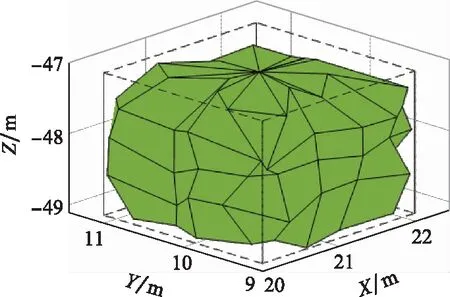
图5 MLS-PMBM跟踪立方体目标时的局部放大图

图8 GGIW-PMBM跟踪立方体目标时的运动轨迹图

可以看出,即使同时跟踪多个目标,MLS-PMBM依然可以准确地估计出各个目标的三维形状,且所估计的形状贴合真实形状。GGIW-PMBM直接将目标形状建模为椭球,不能对复杂形状的三维目标进行形状估计。MLS-PMBM算法可以实现不同目标的三维形状估计,不受目标尺寸变化的影响。因此,MLS-PMBM算法在精度与泛用性上来说,更胜一筹。此外,MLS-PMBM依靠MLS算法的紧支这一性质,可以对同一个量测数据进行多次利用,即一个量测可以更新多个控制点。表2为MLS-PMBM和GGIW-PMBM算法跟踪3个目标时,在形状估计稳定后的平均IoU值。表3为3种算法的单步耗时对比,表中数据均是程序运行100次的平均值。图10是MLS-PMBM的目标数估计,图11是两种算法的OSPA。

表2 MLS-PMBM和GGIW-PMBM算法估计目标的平均IoU对比

表3 算法单步耗时对比

图10 实验1目标数估计

从表2中可知,所提的MLS-PMBM算法对3个目标的形状估计都可以达到较高的精度,稳定后的IoU值均超过了0.8;而GGIW-PMBM算法在跟踪立方体和十字架等不规则形状时,仍然将目标形状建模为椭圆,导致IoU较低,不能实现对目标扩展形状的有效跟踪。从图10和图11可以看出,所提算法对目标数量与质心均有较好的估计效果。图10在目标死亡时会出现目标数错估的现象。这是因为PMBM算法通过全局假设的概率来判定该假设是否被采用。在目标死亡时,包含目标死亡这一状态的全局假设概率小,未被采用;在下个时刻,该全局假设随着状态的更新而概率变大,最终被采用,所以出现了31时刻目标数量不变的现象。表3中的数据表明,同一算法估计不同的三维目标时,单步耗时相差不大。GGIW-PMBM算法的单步耗时低,但是结合实验结果可知,GGIW-PMBM难以估计复杂三维目标的形状细节。综合来看,MLS-PMBM算法能准确估计复杂目标的三维形状,适用性广。

实验 2为了研究MLS-PMBM算法在实际场景中对不规则外形扩展目标的跟踪性能,设计如下实验场景。[-200,200]m×[-200,200]m×[-200,200]m为算法的跟踪区域,3个传感器的位置分别为[250,-200,250]m、[-200,250,250]m和[-250,-250,-250]m。为模拟真实目标外形,借助悉尼大学SYDNEY URBAN OBJECTS 激光雷达数据集中的汽车点云分布获得目标尺寸并进行建模。在跟踪过程中,通过对原始点云数据进行扩充和平移等操作生成目标的量测数据。SYDNEY URBAN OBJECTS数据集通过使用激光雷达扫描悉尼街道景观获得,提供的点云数据中包含扫描点的强度、方位角及三维笛卡尔坐标等信息,其使用的Velodyne HDL-64E LIDAR测量距离可达120 m,测距精度为±2 cm,水平视场分辨率为0.08°～0.35°,垂直视场分辨率为0.4°,较高的探测精度保证了原始点云数据的可靠性。在本实验中,选取的原始点云数据可视化结果如图12所示。MLS-PMBM滤波器的有关参数均与实验1相同。目标1与目标2均为依据点云数据生成的汽车目标,长度为5 m,宽度为1.9 m,高度为1.6 m。

图12 原始点云可视化结果图

表4说明了两目标各阶段的运动状态,模拟目标2加速追上目标1,并排行驶一段时间后,再超过目标1的场景。图13为跟踪过程中单个汽车目标的局部放大图,图14为产生交叉时目标的局部放大图。图15为跟踪过程中算法的目标数估计,图16为算法的OSPA。

表4 目标各阶段运动状态

图13 MLS-PMBM跟踪汽车目标时的局部放大图

图14 目标交叉时跟踪结果局部放大图

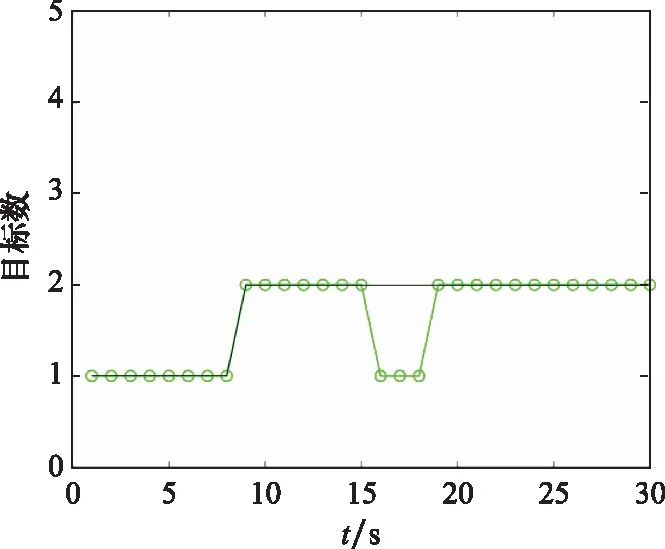
图15 实验2目标数估计

图16 跟踪汽车模型时算法的OSPA

从图13和图14可以看出,对于外形不规则的扩展目标,MLS-PMBM也能够实现对其三维扩展形状的有效描述。但在目标距离较近时,两目标的点云将有一定程度的交叉。由于点云数据未对目标作出区分,经过量测聚类生成的量测簇只有一个,只能分配给一个目标,从而导致目标的外形估计出现偏差。

从图15可以看出,在目标交叉后的第一个时刻,目标数仍然保持了正确的估计。这是因为MLS-PMBM从权重最大的全局假设中提取目标状态,由于交叉时间较短,此时两目标仍然具有较大的存在概率,目标数为2的全局假设权重较大。随着交叉时间的增加,其中一个目标的存在概率下降至阈值以下,包含目标死亡的全局假设权重变大,导致MLS-PMBM产生了漏检。从图16可以看出,所提算法对不规则外形扩展目标的质心有着良好的估计效果。上述实验表明,MLS-PMBM 能够实现对多个实际目标的质心和形状跟踪,验证了所提算法的泛用性。

4 结束语

本文针对三维空间下的多扩展目标形状估计问题,提出了在多传感器的情况下,基于MLS模型的多目标PMBM滤波器。算法将融合后的量测数据输入至PMBM滤波器,对目标的质心运动状态进行迭代更新,通过MLS模型并结合量测数据计算形状矩阵中移动后的控制点,最后将目标质心状态与形状矩阵结合得到三维目标的扩展状态。仿真实验和实际点云数据的验证表明,与GGIW-PMBM相比,所提算法在不规则形状扩展目标的形状估计方面具有更高的精度,能够有效应用于实际场景中。

在实际场景中,激光雷达扫描得到的点云数据来自于各类目标,为了保证跟踪精度,需要对原始点云进行分割分类等预处理,从而实现不同目标量测数据的区分。当目标之间出现邻近、遮挡等特殊情况时,将会使来自不同目标的点云数据相互交叉, 导致MLS-PMBM算法对目标数量和扩展形状的估计产生错误。针对上述问题,本文的下一步工作,是对MLS-PMBM的聚类算法进行改进,充分利用点云数据中的扫描点强度等信息,实现更加精准的点云分割分类,提高算法在复杂场景中的适用性。