机器人室内自主载人自适应性匈牙利派单算法
高庆吉,粟 鹏,佘亮亮,邢志伟
(中国民航大学 中国民航大学机器人研究所,天津 300300)
0 引言
航站楼等大型公共室内环境中,经常采用载客小车运送客人到达目的地,是目前已经存在的便捷旅客乘离的服务模式。但是,所用车辆一般都是人工驾驶,旅客的可选择性和自主性受其制约,故航空出行的体验没有得到很好提升[1]。受共享出行理念的启发[2],提出“室内网约车”的概念。采用自主载人机器人作为“室内网约车”,搭载旅客和行李,将旅客自主运送到登机口等目的地,不仅可以压缩旅客在楼内的行走时间,而且将大大提升出行体验,具有重要的价值和意义。同时,考虑投入载人机器人为旅客解决航站楼“最后一公里”的出行问题,需考虑旅客的动态接载需求,建立自适应性的调度策略,以提高旅客满意度是非常有必要的[3]。
但是基于航站楼载人机器人应用场景的派单特殊性,实现载人机器人的派单模式还需进一步探索。Lee[4]等通过分析基于最近坐标法的司乘直线距离最短的派单方式,提出了基于实时交通状况的派单新方案,并建立了以司机到达载客点的时间最短为派单规则;Hanna[5]等学者的同类问题研究中,对无人驾驶共享汽车中的订单分配问题进行了研究,在乘客和车辆数量不断发生变化的动态场景中,把乘客和车辆的匹配问题转化为二分图匹配问题,研究了基于候车时间最短的匈牙利算法,并根据全域最优策略,对算法进行改进,提出了集中式贪心算法和匈牙利算法的组合优化算法;YE[6]等将网约车大规模订单调度定义为NP问题,使用组合优化等算法予以解决;张进[7]等对比分析传统匈牙利算法与智能优化算法的耗时性与稳定性,展现了匈牙利算法的优势,并提出统一效率矩阵,所改进的匈牙利算法可适用于各类型的目标分配;Maciejewski[8]等根据连环派单的思想,遵循先到先服务的原则,对空车与非空车进行综合考虑,把订单分配给接驾时间最短的车辆,从而缩减了司机的接驾距离和乘客的候车时间。
上述研究主要为不断优化网约车派单调度[9-10]和多机器人调度[11-13]等内容,而共享出行的理念对本文涉及问题有借鉴价值。对于大型公共室内环境自主载人,需考虑空间范围、人流密度、航班时刻分布及机器人载运能力等条件的约束,以及最短候载时间和机器人群体最低能耗的目标要求,从而建立相应的载人机器人派单算法。
1 航站楼派单业务场景建立
对于航站楼载人机器人派单空间,将以安检口到各登机口区域作为载人机器人的可行域,为旅客提供便捷乘机服务。其中“室内网约车”模式相比于城市网约车异同点如下:
1)采用调度时间窗口,并延时集中批量处理订单匹配,实现了略微更“全局”的优化。
2)二分图匹配问题,一边为需求侧,一边为供给侧,派单算法快速解决双方的匹配关系。
其中两者区别主要体现以下方面:
1)应用场景不同。航站楼载人机器人应用于动态高密度人流的室内环境[14],受其固定可行区域中障碍物环境的约束,且单个载人机器人只可载运单个旅客。而网约车应用于动态高密度车流的城市路网,受其交通管制约束,并将城市地图划分为无数个六角形的网格图,每个网格图代表一个派单单元区域,且单个司机车辆只可搭乘单个或多个乘客。
2)处理RP(route planning)路线规划不同。航站楼载人机器人的路径规划算法是每个空闲载人机器人访问目标旅客,实时规划出一条适合机器人在航站楼环境中行走的路径。而网约车平台计算路线规划是基于城市路径拓扑图,其接驾的路线规划代价是基于城市路网导航距离,而并非基于坐标的欧式距离。
3)派单软件平台组成不同。“室内网约车”则是分为载人机器人端、旅客端和派单服务端。网约车平台主体分为司机端、乘客移动端和派单云平台。
故研究载人机器人的可行域时,主体考虑安检通道至各登机口区域,由航站楼各指廊等部分组成。如图1所示,如果以安检口为起点,各登机口为终点,其主体载人机器人在隔离区(安检口—登机口区域)内服务,并在隔离区设置其类似城市路网及调头地标等服务信息,主体以安检口和登机口之间的旅客运送和返回为主要形成,时而有中间接载旅客的服务。

图1 派单主体区域示意图
其旅客搭乘起点主体以安检出口为主,即载运等候区。其他起点可遍布于隔离区各处,而载运抵达的目标主体以遍布隔离区各处的登机口为主,当然也可以按照需求旅客指定确认的目的地点位,如购物餐饮等。由此在隔离区空间中存在用车需求的情况时,可考虑实行平台派单模式,为全域需求旅客提供其载运服务。此时接载起点不仅仅为安检通道的起点,也可以是隔离区域中的任意一点作为起点,抵达隔离区的目的地,构建起终点(OD,orignation-destination,起点-终点)间的交通出行量[15-16]。
2 接载派单规划原理
2.1 二分图派单思想
探索航站楼载人机器人平台派单算法,是对载人机器人和旅客接载任务的高效匹配。如图2所示,对于航站楼载人机器人系统将充分共享服务端平台[17],满足需求旅客高效位移的需求,各载人机器人在派单平台上为特定的IP点(internet protocol),系统将进行实时采集机器人状态信息,以获取可调度载人机器人在室内环境中的坐标信息,并将呈现为在空间中的供给点,当载人机器人接到云端指令时,将前往某个位置接载旅客,或路上遇到旅客招手后将停车接载。而需求旅客作为移动端,发起使用需求时,将呈现为在空间中的需求点,当旅客看到机器人后做手势搭乘,同时载人机器人移动到旅客身边提醒旅客搭乘。

图2 平台派单系统架构示意图
由此建立了航站楼空间派单平台,如图3所示,其载人机器人概念如图4所示。菱形点为需求旅客,构造出载人机器人与需求旅客两个集合,其中集合分别为Ci={c1、c2、…、ci}、Pj={p1、p2、…、pj},形成了具有互不相交的两个子集,构建两个集合后,将定义一个边对两个集合中的点与点实时匹配连接,并赋予一个权重代价值f,构建一个二分图数学模型,故载人机器人和需求旅客匹配为二分图匹配问题(bipartite graph mathing)[18-21]。

图3 空间派单二分图示意图

图4 载人机器人样机图
2.2 接载OD矩阵
针对以上二分图关系,将基于室内栅格化地图,计算各载人机器人访问全域需求旅客的路径代价。且航站楼载人机器人的路径规划需满足高效计算,故利用JAVA软件将A*路径规划算法构建为RP(route planning)服务器。将全域栅格地图利用0~1表示(0为自由区域,1为障碍区域),构造为栅格地图的0~1矩阵,保存至RP(route planning)服务器。由此利用A*路径规划算法从起点逐步计算至终点,并形成多线程访问路径规划,得出全域多载人机器人到目标需求旅客的预估接载路径代价。因为空间中的载人机器人将基于A*算法同时进行大量的路径访问需求,所以假设在2 s时刻,空闲载人机器人的数量为M(渗透率计算),需求旅客人数为N(旅客抵达航站楼服从泊松规律),则在2 s时刻时路径访问次数为Y=M*N,呈线性增长关系。
假设需求旅客p1,p2,…,pj,其中位置信息为(xj,yj),载人机器人c1,c2,…,ci其中ci(i=1,2,…,i,i∈M),位置信息为(xi,yi)。利用路径规划算法计算载人机器人到每位需求旅客pj(j=1,2,…,j,j∈N)的路径代价为rij。故以载人机器人自身为源点,以需求旅客为终点,构建接载OD矩阵M所示:
因此,构建载人机器人计算当前访问需求旅客状态时,若只考虑接载任务距离,其预估个体需求旅客大致平均等待时间为:
(1)
其中:vij表示载人机器人移动的平均速度。若引入城市网约车道路交通状态分析,将利用机器人平均行驶速度来描述航站楼通行的拥挤程度。故载人机器人在执行接载任务期间的行驶时间不仅取决于任务节点之间的距离,还取决于周围人流密度的影响。故引入环境路况因子δ(route)ij表述旅客密度ρ对载人机器人行驶速度的影响,并根据格林希尔兹模型[22-23],得到旅客密度与航站楼载人机器人速率的影响及预计到达时间,并建立相关公式如下:
(2)
(3)
(4)

(5)
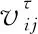
2.3 接载派单数学模型
针对调度时段范围内,研究其需求旅客与载人机器人存在动态供需不平衡等情况时,以全域最优派单算法解决派单匹配问题。假设在Δt=2 s时,航站楼空闲载人机器人数量为m,需求旅客数量为n,并且每次接载任务为一对一达成合乘的接载服务。令其Pn={p1,p2,…,pn}代表全域的需求旅客,集合Cm={c1,c2,…,cm}代表全域编号的载人机器人。若载人机器人ci与需求旅客pj关联,则载人机器人访问到需求旅客得出的路径代价为rij,建立其访问路径矩阵M的基础上,将考虑个体载人机器人所处的环境因素,其中包括接载路径、旅客等待时间和机器人能耗,即路径-时间-能量的调度模型,并将3个指标分别考虑融入权重w1,w2,w3,得到适应度函数值fij作为匹配的权重值,由此整理构建为二分图接载任务OD矩阵ODij,可以表达为:
同时,在建立航站楼全域载人机器人访问接载任务适应度值最小为原则,以获取全域载人机器人接载派单矩阵。因此在获取需求旅客与载人机器人的派单关联策略时,即求解关联策略的状态变量矩阵C,其为i×j的矩阵,各元素为{0,1},即cij={0,1}。故对载人机器人—需求旅客的派单关联过程进行建模,其目标函数以fij为自变量,fij与cij有关。故利用组合优化算法以约束原则求出其派单关联矩阵,进而对全域载人机器人进行派单。此时得出对应的状态变量矩阵C=[cij]i×j为派单关联矩阵,令其派单关联矩阵为M,此时M=C。
目标适应度函数:
(6)
M=C=[cij]i×j
(7)
约束条件:
(8)
(9)
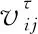
2.4 接载派单原理分析
将载人机器人考虑动态供需不平衡的派单问题时,主体考虑平衡目标分配和不平衡目标分配[24],假设空闲载人机器人数量为m,需求旅客数量为n。当两者人数不相等时,将添加附近快到达目标点的载人机器人和虚拟需求旅客,以增加二分图接载任务OD矩阵中派单的可行解,以解决不平衡目标分配等情况:
1)假设添加虚拟需求旅客,将实行加边补零法,零则表示添加访问虚拟需求旅客适应度函数值fij=0,使其派单矩阵形成方阵,再采用派单规划算法进行计算。
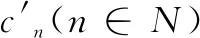
2.5 自适应接载派单算法
为此设计各种载运供需场景的派单求解算法的流程,具体自适应性匈牙利算法流程步骤如图5所示。

图5 自适应性匈牙利算法流程图
3 仿真实验与结果分析
3.1 小规模环境派单实验
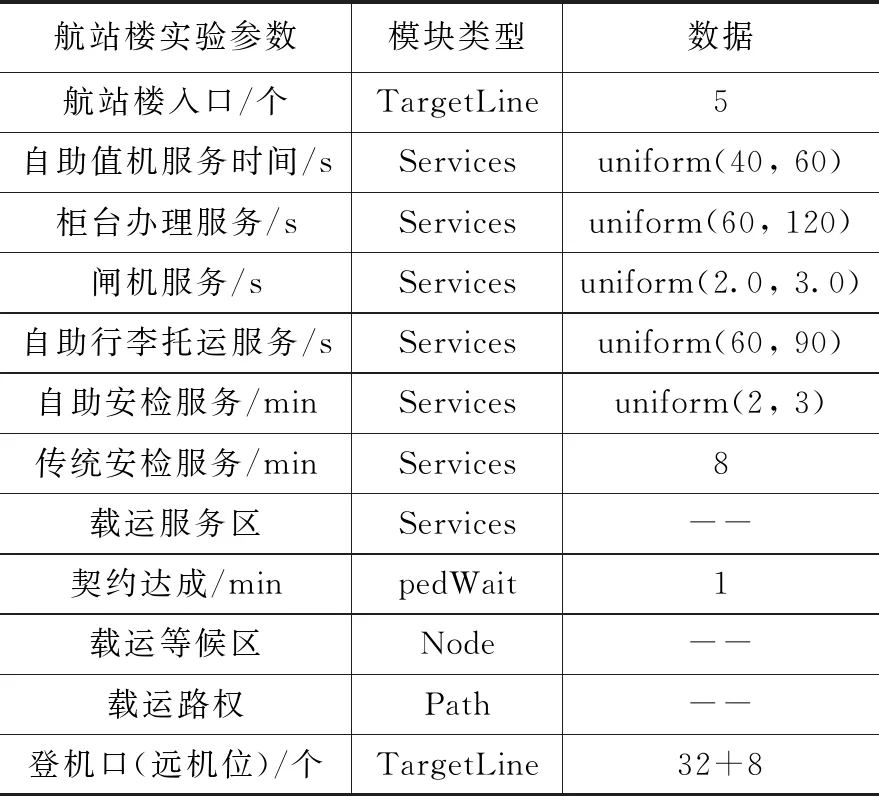
在MATLAB软件中进行小规模派单仿真实验:在处理派单匹配时刻,给定其6个载人机器人和6个需求旅客的信息如表1所示。

表1 当前状态信息表
其中,Nt=2 343人,S0=25 000 m2,vf=4 m/s,ρs=0.204 28,i=6,j=6,w1=0.3,w2=0.3,w3=0.3,U0=24 V,I0=8 A。根据航站楼实际路况,其列出路况因子信息,并求得各载人机器人访问目标需求旅客路径代价值。得到结果如表2所示。

表2 访问目标需求旅客路径代价rij信息表
由此计算得出二分图接载任务矩阵,即载人机器人访问各需求旅客的目标适应度函数值,如下矩阵ODij所示:
根据二分图接载任务ODij矩阵可知,载人机器人分配不同需求旅客会获得不同目标的适应度函数值fij,并通过自适应性匈牙利派单算法以分配接载目标。
由此针对各类动态供需场景的派单问题时,将以载人机器人与需求旅客数量关系研究派单求解实验。如下将主体分为供需平衡和供需不平衡条件的派单实验。
1)载人机器人供需平衡条件的实验:
如图6所示,图中对比出自适应性匈牙利派单算法能满足其就近派单,并以此约束全域需求旅客接载时间最短,反之模拟退火算法得出派单结果较差。其中对于自适应性匈牙利算法得出其全域接载适应值和比模拟退火算法小20%。同时,在具体接载任务分配上面,模拟退火算法将C6分配给了P3,C4分配给了P4,这样会导致P3旅客等待时间较长。而自适应性匈牙利算法得出的派单规划,将C6分配给了P4,C4分配给了P3,使其P3和P4旅客等待时间都能接受,也充分满足了将就近的载人机器人派给需求旅客。

图6 两种算法的分配结果示意图
2)载人机器人供需不平衡条件的实验:
(1)机器人多时,即m>n。如图7所示,在全域载人机器人数量多于需求旅客时。两者都是添加虚拟需求旅客,将二分图接载任务ODij矩阵计算,最终得出了派单结果均满足就近原则和结果的一致性。
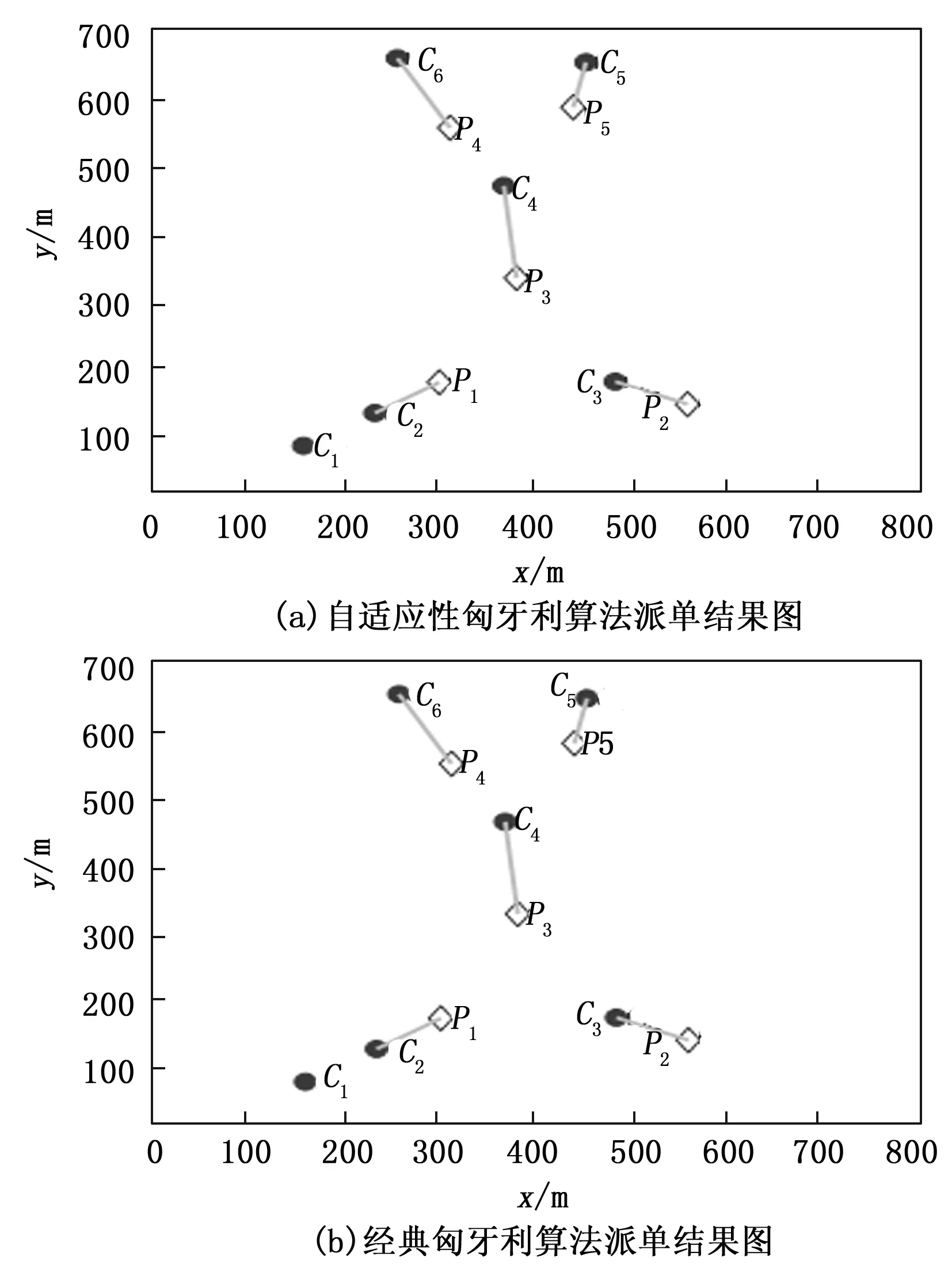
图7 两种算法的分配结果示意图
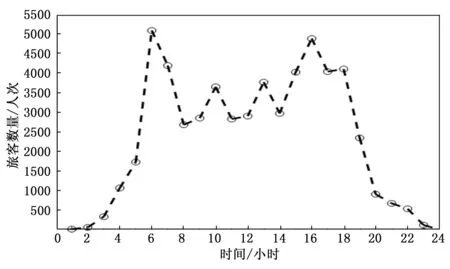
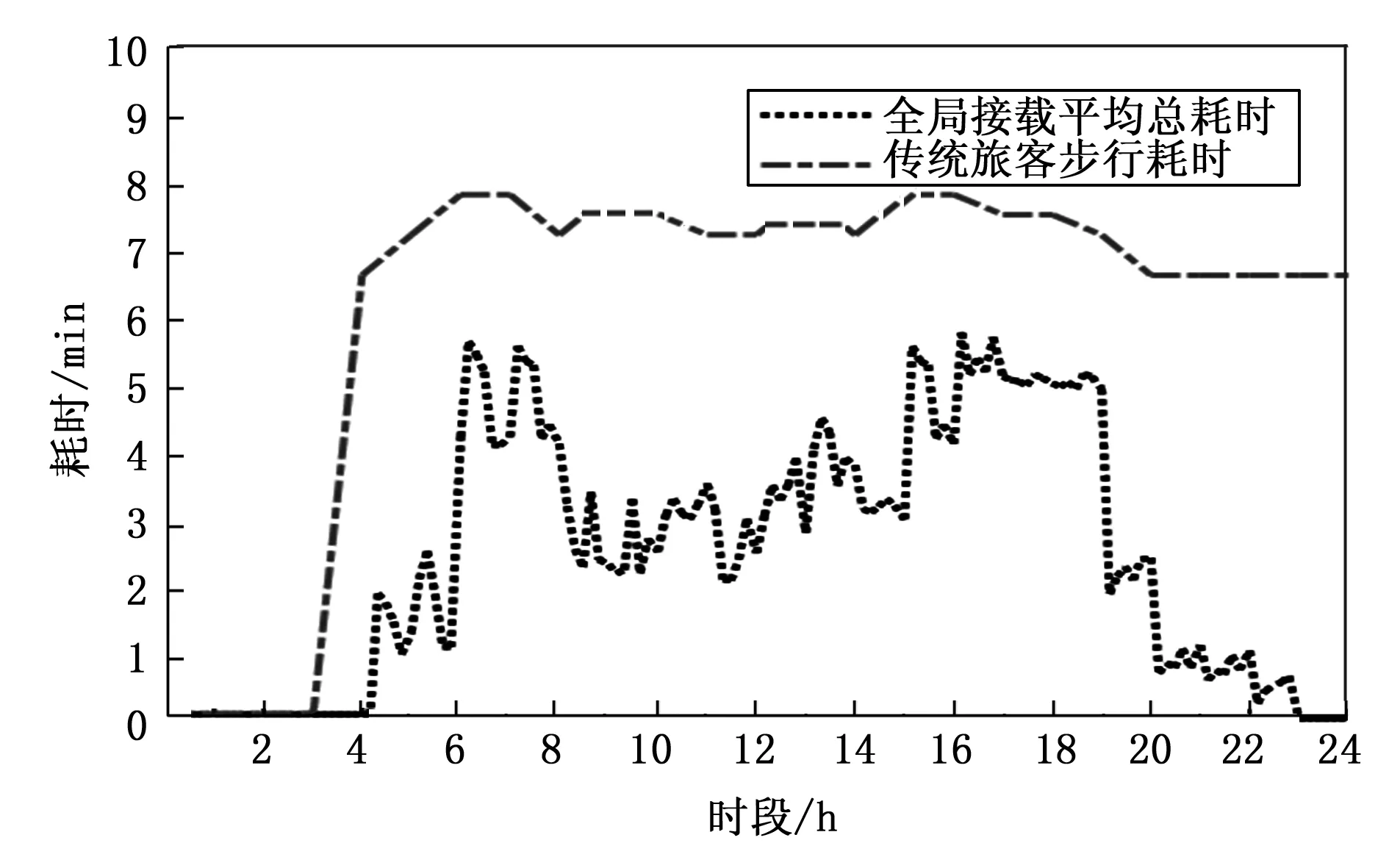
(2)旅客多时,即m 图8 两种算法的分配结果示意图 综上对小规模动态供需不平衡派单匹配的计算,既基于旅客密度-时长-能耗模型设计了载人机器人的二分图接载任务ODij矩阵,同时涵盖了三类供需不平衡场景时,对该派单矩阵处理的策略。故将统一建立基于微小调度时窗内(Δt=2 s)批量派单处理,以得到全域的最优指派规划,并充分满足全域需求旅客的就近派单,提高需求旅客的满意度。 以上利用软件构建了航站楼载人机器人的自适应性匈牙利派单算法,并对小规模动态供需不平衡派单匹配进行计算分析。故针对大规模模拟航站楼派单场景的仿真实验时,将利用Anylogic软件进行场景搭建及实验,其中整理了相关模拟航站楼的实验参数数据,包括实验统计日期为2018-01-31。其详细采集数据如表3所示。 表3 航站楼的实验参数数据表 同时建立了航站楼便捷乘机规划,在模型中的逻辑乘机服务模块参数如表4所示。 表4 航站楼的便捷乘机规划服务模块参数表 并且在航站楼的便捷乘机规划中,包括了安检口至登机口的隔离区作为派单可行区域,也是考虑载运的便捷通行区域。由此对于派单区域的需求旅客,主体考虑其隔离区人流的用车需求,不仅来源于隔离区旅客的用车需求,同时服务快速离港乘机通道的旅客。因此,统计了该航站楼模型在隔离区各时段旅客人数,如图9所示。 图9 航站楼各时段隔离区旅客数量分布图 由图9看出,其密集人流主要集中在早高峰和下午16点左右。利用其航站楼便捷乘机规划Anylogic的模型,当离港人流分布流速为ni时,即设置每小时抵达人数的速率。由此统计其对应全域载人机器人整体平均耗时t,并作出t关于ρ的变化曲线,如图10所示。 图10 平均接载耗时随密集人流变化图 由此结合图9和图10可得载人机器人速率变化规律: 由此在Anylogic模型中设计出主体需求旅客的离港流程并搭建航站楼整体三维模型,并特别将航站楼模型运行当日高峰小时流量场景,得到全流程航站楼整体模型的人流密度,如图11所示。 图11 航站楼人流密度分布图 同时对于航站楼模型将考虑全域载人机器人服务需求旅客的渗透率,其中整体服务人流来自于传统乘机模式与便捷乘机模式,即研究载运区占比主体服务人流的渗透率大小。在不同渗透率大小时,对比需求旅客使用载人机器人与传统步行的耗时对比,进而得出投入航站楼载人机器人的必要性。由此在隔离区(安检口—登机口)区域,得出全域载运需求旅客的耗时与传统步行模式时间对比变化规律,如图12所示。 图12 全域平均接载耗时对比图 横坐标即投放载人机器人服务人流占比,即渗透率,由此得出其载人机器人与传统步行的耗时分析,得出其载运耗时明显低于传统步行的模式,其平均节约4 min左右。 由此,将派单算法实时计算航站楼全域载人机器人接载路由(Δt=2 s)及全域旅客预估等待时间,处理延时集中派单请求,并统计其一天24 h的实验结果,如图13所示。 图13 航站楼24 h派单接载耗时统计图 最终,运行主体航站楼模型24 h派单统计实验,得出整体便捷乘机规划与传统乘机流程耗时对比图,旅客使用载人机器人比传统步行耗时具有明显优势,平均节约4 min左右,并且在高峰时段也能满足需求旅客用车请求。 综上所述,整体得出将航站楼载人机器人投放至安检口-登机口区域服务时,突显其便捷快速等优点,同时引用共享出行模式建立载人机器人的派单算法,以提高离港需求旅客出行的满意度。 针对类似航站楼大型公共室内环境,研究载人机器人与需求旅客数量动态供需不平衡而引起的派单优化问题,借鉴了网约车派单优化策略,将航站楼载人机器人供需关系和连环派单情况加入考虑范畴,提出了自适应性匈牙利派单算法。实验验证了在小规模派单实验时,得出全域机器人整体接载适应值,相比较模拟退火算法减少20%;并且相比经典匈牙利派单算法,引入了连环派单能够增加全域派单求解的可能性。同时在大规模航站楼场景派单统计实验中,结合航站楼旅客时空分布规律,得出了在不同渗透率时,机器人接载耗时比传统旅客步行耗时平均节约50%,而且整体形成的便捷乘机模式比传统乘机模式节约了43%。故对于类似航站楼室内动态的人机交互环境中,所研究的自适应性匈牙利派单算法具有应用参考价值。
3.2 大规模派单实验




4 结束语

