六相直线感应电机模糊间接矢量控制

张振宇，汪光森，王 康，王志伟

(海军工程大学 舰船综合电力技术国防科技重点实验室，武汉 430033)

0 引言

直线电机是一种无需中间转换结构，直接将电能转化为直线运动机械能的电磁传动装置[1]，因其结构简单、可靠性高、控制性能好，在轨道交通、矿井提升、电梯驱动、飞机弹射等多种场合有着广泛应用[2-3]。在电机应用于复杂场景时，如电机运行于水中，由于水体运动的复杂性，而且可能受到一些非线性的、时变的、无法预测的外部干扰，因此往往难以建立电机与水体系统的准确模型。工程上常用的比例-积分-微分(PID，proportional integral derivative)控制等，参数的整定需要准确的系统模型，在这类场景下，往往需要多次尝试进行参数的整定，较为复杂耗时，且控制精度不高，适应性也较差[4]。

模糊控制是一种建立在自然语言控制规则、模糊逻辑推理基础上的控制算法，它将被控对象看成一个“黑箱”，通过由操作经验、表述知识等转换成的“模糊规则”，实现对被控对象的控制[5]，因此无需准确的数学模型，很适合复杂、非线性、时变的控制系统[6]。模糊控制经过多年的发展，目前已经在炼钢、化工、家用电器等多个领域应用。在电机控制方面，相关研究也有很多。如文献[7]利用模糊神经网络的非线性逼近能力构建了电机的逆系统，从而实现了对原系统更好的解耦。文献[8]利用模糊控制原理为电机最大再生制动力分配系数，从而提高了再生制动能量的利用率。模糊控制算法也可以与其他先进算法结合，更好的用于对电机的控制。文献[9]将模糊控制算法与滑模控制结合，通过模糊控制算法调节滑模增益，提高了滑模控制的抗扰能力，并削弱了抖振的问题。文献[10]采用模糊控制算法取代模型参考自适应算法的PI调节器，对电机转速估算，使得算法能够更好适应负载的波动。文献[11]采用模糊控制算法调节有限集预测代价函数中权重系数，有效地抑制了转矩和磁链脉动。

模糊控制也较多的应用于电机控制中的速度环。文献[12]在转速环中采用模糊自适应PI控制算法，改善了传统PID响应速度慢、超调大等问题。文献[13]以转速的偏差及其变化率作为模糊控制算法的输入，以参考电流值作为输出，提出了一种基于速度环模糊参数自适应的PID算法，该算法相比于传统的PID具有更好的鲁棒性。文献[14]将分数阶积分与分数阶微分引入模糊控制器中，设计了一种模糊分数阶PID转速外环控制器，提高了电机系统的控制性能。文献[15]提出了一种变论域自适应模糊PID复合控制策略，并将其应用到基于矢量控制的永磁同步伺服系统的速度环中，提高了系统的鲁棒性和抗扰能力。但模糊控制在用于速度环时，多是通过调节PID参数来改善系统的动态性能，由于PID参数较多，使得模糊规则较为复杂，调试也较为耗时。

为了实现电机在复杂环境条件下的准确控制，本文将模糊控制算法应用于六相直线电机间接矢量控制的速度环，以位移和速度的偏差为输入，经过模糊推理直接得到反馈电磁力，避免了复杂系统的建模和对PID参数的整定，且相比于模糊调节PID参数的方法，只有一个模糊输出量，控制规则更少。另外通过对隶属函数、模糊控制规则的优化选取，并采用隶属函数分区和中心法，减小了计算量，从而实现了算法的实时计算。最后通过仿真和半实物仿真平台对所提算法进行了验证，结果表明所提算法能够实现位移和速度对参考值的良好跟踪，且通用性好，能够实现复杂环境下直线电机的准确控制。

本文后续章节安排为，第一节介绍了六相直线感应电机的建模过程，以及间接矢量的控制方法。第二节阐述了模糊控制算法及其与电机控制算法的结合，第三节展示了仿真及半实物仿真平台的验证效果，最后第四节对全文进行了总结。

1 六相直线感应电机间接矢量控制

1.1 六相直线感应电机模型

本文被控对象为六相直线感应电机，六相绕组为半对称结构，两套绕组互差30°电角度。绕组联结方式如图1所示[16]。

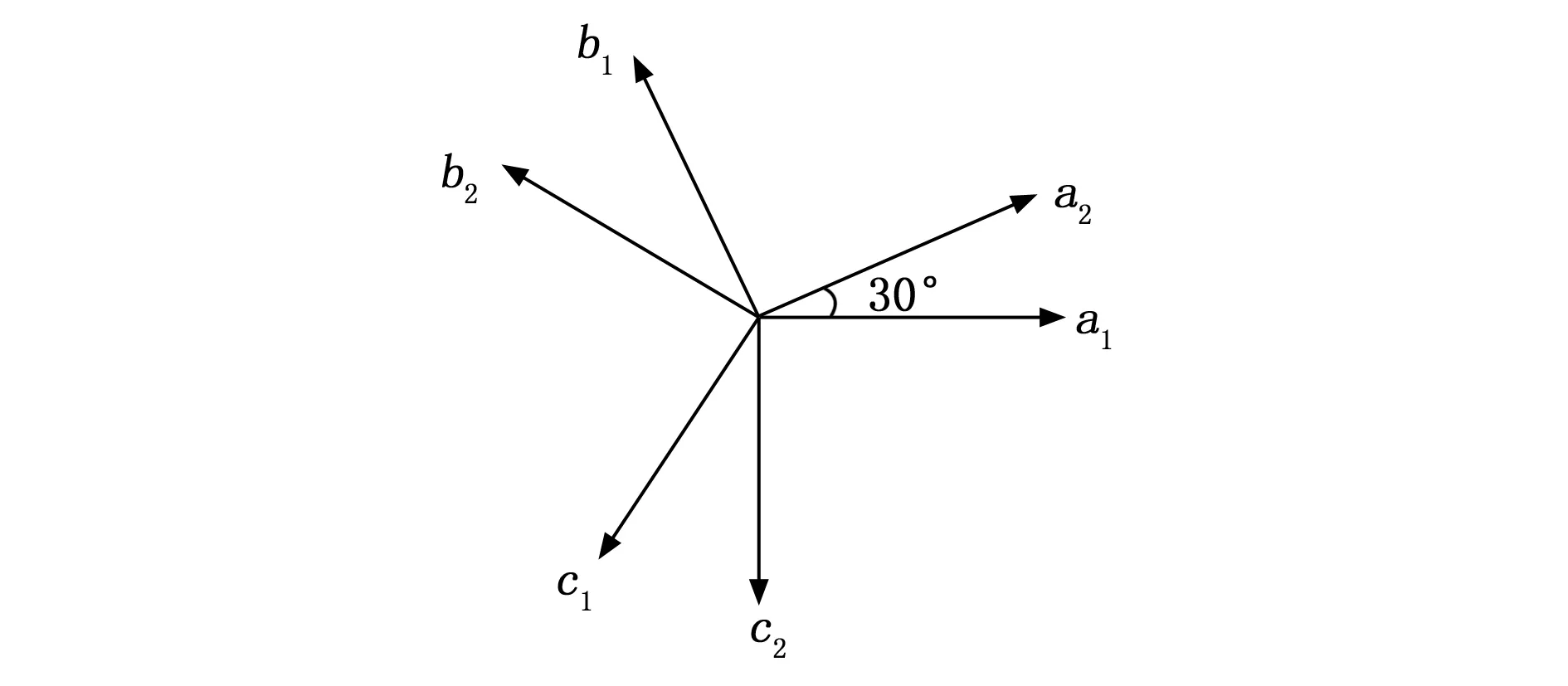
图1 直线电机初级绕组分布

在电机模型建立前，作如下的假设：1)忽略空间谐波的影响；2)忽略铁芯磁滞和铁心损耗；3)忽略频率和温度变化对绕组电阻的影响；4)由于初级绕组极数较多且动子运动速度较低，忽略边端效应。在自然坐标系下，六相直线电机的磁链和电压方程可以表示为[17]：

ψs=Lssis+Lsrir

ψr=Lrsis+Lrrir

(1)

us=Rsis+pψs

ur=Rrir+pψr

(2)

式中，ψs、ψr为定子和转子磁链，Lss、Lrr为定子和转子的自感矩阵，Lsr、Lrs为定转子的互感矩阵，us、ur为定子和转子电压向量，is、ir为定子和转子电流向量，Rs、Rr为定子和转子电阻矩阵，p为微分算子。

由于六相电机的数学模型是一个高阶、非线性、强耦合的多变量系统，考虑通过坐标变换，将两个三相分别变换到同步旋转坐标系中，实现解耦控制。在同步旋转坐标系下，磁链方程为[18]：

ψsd1=Lsisd1+Lmisd2+Lmird1+Lmird2

ψsq1=Lsisq1+Lmisq2+Lmirq1+Lmirq2

ψsd2=Lmisd1+Lsisd2+Lmird1+Lmird2

ψsq2=Lmisq1+Lsisq2+Lmirq1+Lmirq2

ψrd1=Lmisd1+Lmisd2+Lrird1+Lmird2

ψrq1=Lmisq1+Lmisq2+Lrirq1+Lmirq2

ψrd2=Lmisd1+Lmisd2+Lmird1+Lrird2

ψrq1=Lmisq1+Lmisq2+Lmirq1+Lrirq2

(3)

式中，Lm为激磁电感，Ls为同步坐标系下初级绕组漏感，Lr为同步坐标系下次级绕组漏感。下标d表示d轴分量，下标q表示q轴分量，下标1和2用于区分两套三相绕组。

电压方程为：

usd1=pψsd1-ωeψsq1+Rsisd1

usq1=pψsq1+ωeψsd1+Rsisq1

usd2=pψsd2-ωeψsq2+Rsisd2

usq2=pψsq2+ωeψsd2+Rsisq2

urd1=pψrd1-(ωe-ωr)ψrq1+Rrird1

urq1=pψrq1+(ωe-ωr)ψrd1+Rrirq1

urd2=pψrd2-(ωe-ωr)ψrq2+Rrird2

urq2=pψrq2+(ωe-ωr)ψrd2+Rrirq2

(4)

式中，ωe为同步旋转角速度，ωr为转子旋转角速度。

电磁力方程为：

Fe=βLm[(isq1+isq2)(ird1+ird2)-(isd1+isd2)(irq1+irq2)]

(5)

式中，Fe表示电磁力，β=π/τ为波长系数，τ为电机极距。

1.2 间接矢量控制算法

电机采用间接矢量控制，主要原因是本文所研究的直线电机，工作时间较短，对响应速度要求较高，间接矢量控制采用开环磁通控制，属于前馈控制的思想，具有响应速度快的优点[19-20]。当采用转子磁场定向，即令d轴与转子磁链的方向重合，磁链的q轴分量为0，即：

ψrd=ψr

ψrq=pψrq=0

(6)

转子绕组电压为0，根据式(4)与式(6)，得到：

(7)

式中，ωs为滑差频率，ωs=ωe-ωr。

根据式(3)、式(6)和式(7)，可以求出转子磁链和滑差频率如下：

(8)

(9)

根据式(3)和式(5)，得到电磁力的表达式：

(10)

对电机的两个三相采用相同的控制策略，其中一个三相的间接矢量控制算法原理如图2所示。图中上标*代表给定值。x、v、a为位移、速度和加速度。ACMR为电流励磁分量调节器，ACTR为电流转矩分量调节器。Fp为前馈力，由给定的速度和加速度决定，Ff为反馈力，由速度环计算得到。

2 模糊控制算法

由图2可知，给定的命令电磁力包括前馈力和反馈力两个部分，对于反馈力的计算，传统上一般采用PID控制的方法，但是PID参数的整定依赖于准确的系统模型，且较为复杂。因此考虑在原有间接矢量控制的基础上，将模糊控制用于速度环，避免了复杂的系统建模和参数整定过程。模糊控制算法的原理如图3所示[21]。

算法的原理为：以位移和速度误差作为输入，经量化因子放大，再通过隶属函数模糊化，按照预先设定的模糊控制规则进行模糊推理，将推理的结果采用中心法进行清晰化，并通过比例因子放大，得到反馈电磁力作为输出。由于仅有两个输入和一个输出，因此整个模糊控制算法计算量较小。

输入和输出论域选定范围为[-5，5]，这样可以使隶属函数的解析表达式更加简洁。量化因子的选择则要根据运行工况下的最大偏差来确定，本文选定速度偏差范围为[-0.5，0.5]，位移偏差范围为[-0.05，0.05]，因此速度误差对应的量化因子设定为10，位移误差对应的量化因子设定为100。由于实际工况存在一定的干扰，实际误差可能会超出该误差范围，对于这种情况，则按照最大误差处理。例如对于位移误差为0.06 m/s的情况，则按照位移误差为0.05 m/s处理。对于比例因子的确定，则要根据实际的工况进行调节。在实验前，可以根据经验对比例因子设定一个大致范围，实验时，再根据调节效果适当增大或减小比例因子，相比于PID需要整定3个参数，该方法更为简单。

2.1 隶属函数与模糊控制规则

隶属函数一般采用三角形或者高斯型，考虑到计算量，采用三角形隶属函数，且仅使用5个模糊子集{NBNSZOPSPB}，分别代表负大、负小、零、正小、正大。采用的三角形不完全相同，因为在输入量较大时，调节较为粗糙，在输入量较小时，调节更为精细。输入隶属函数的形式如图4所示。

输出隶属函数形式如图5所示。

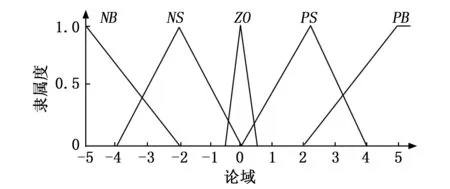
图5 输出隶属函数示意图

隶属函数形式较为简单，其表达式都是线性函数，因此计算量很小。且由于隶属函数都是关于0轴对称的，因此实际仅需存储横轴正半部分的函数，对于负半轴的计算，直接取绝对值，即可求出相应的隶属度，因此函数存储可以减少一半。

为了实现较好的控制效果，需要制定合适的模糊控制规则。本文所制定的模糊控制规则如表1所示。

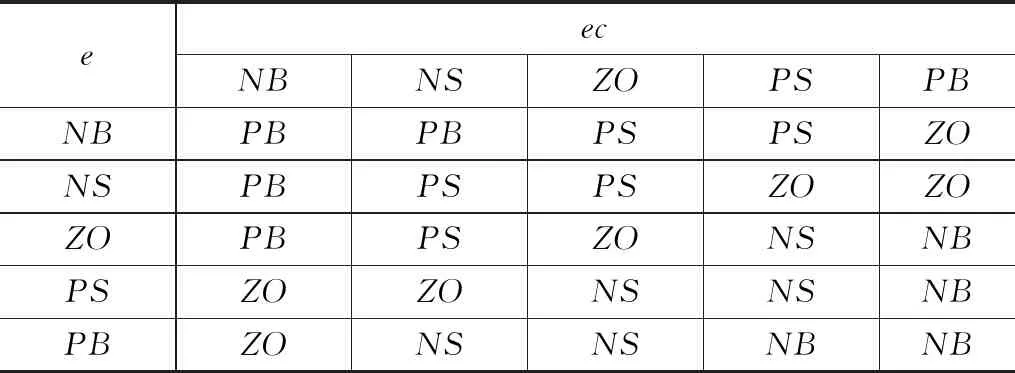
表1 模糊控制的规则

表中：e表示位移误差，ec表示速度误差。

模糊控制规则遵循：当速度和位移误差同为负时，说明实际速度和位移小于参考值，给定的电磁力偏小，此时应当增大电磁力，且误差越大，补偿力的绝对值应当越大；当速度和位移误差同为正时，说明实际速度和位移大于参考值，给定电磁力偏大，此时应当减小电磁力，且误差越大，补偿力的绝对值应当越大；当速度和位移误差不同正负号时，此时应当根据二者误差大小确定补偿力的正负以及合适的值。总体而言模糊规则数目较少，实现较为简单。

2.2 近似推理与清晰化

由表1可知，一共有25条模糊控制规则，如果每次计算都调用25条规则进行推理，计算量很大，因此考虑采用分区的方法[22]，筛选出有效的控制规则，从而减小计算量。输入隶属函数分区如图6所示。

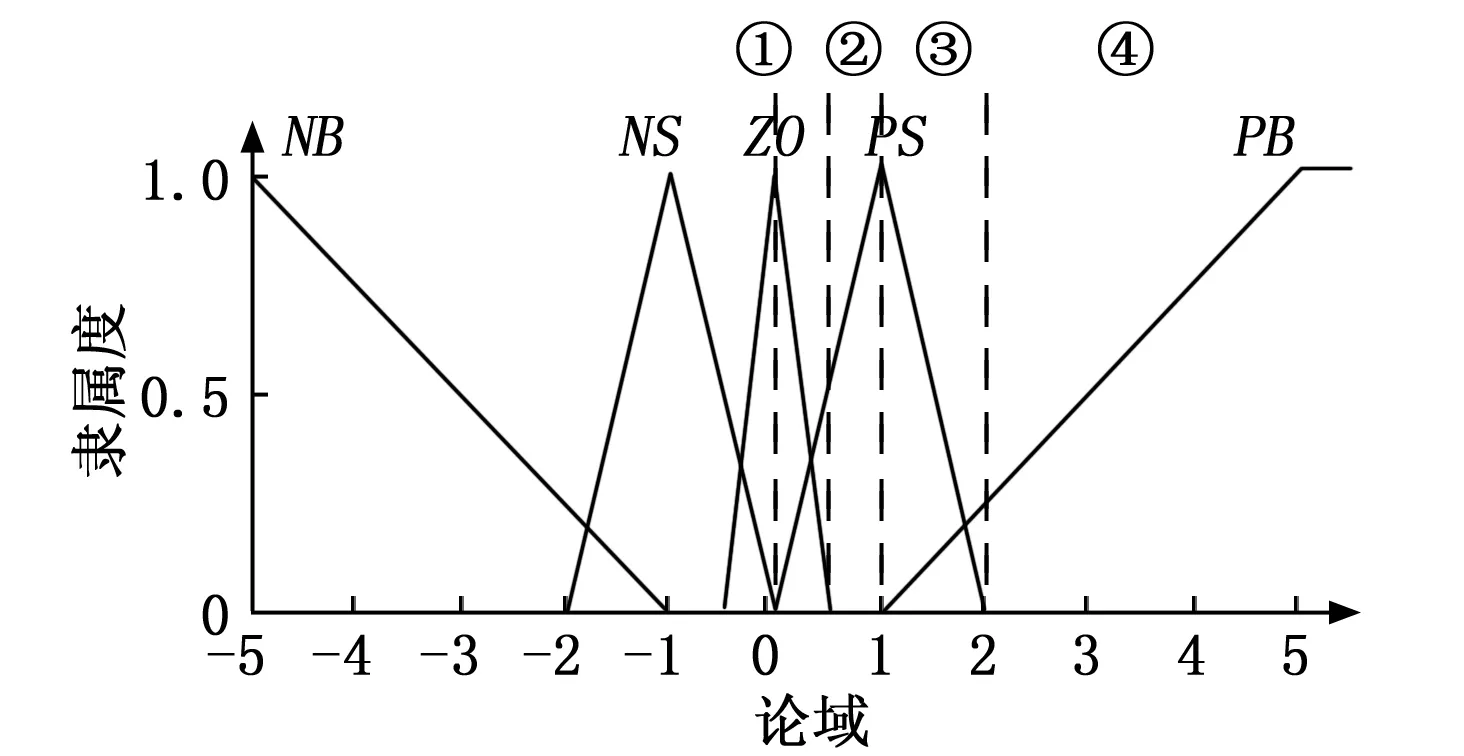
图6 隶属函数分区示意图

鉴于隶属函数关于0轴对称的，因此只对正半轴进行分区，分区的依据是该区域内包含隶属函数的数目，例如，在①区有ZO和PS两个子集，而②区只有PS一个子集。通过分区，可以确认有效的模糊子集，其余不含有效模糊子集的控制规则不用考虑，从而减小模糊推理计算量。

选择有效控制规则，采用Mamdani算法进行推理[23]，得到的结果需要经过清晰化，转换为具体的数值。清晰化一般采用重心法，但是重心法的计算量较大，考虑采用文献[24]中的中心平均法，其计算结果与重心法较为接近，且计算量较小。中心平均法具体计算方法为：

(11)

根据隶属函数和模糊控制规则，我们可以得到模糊推理输出曲面，如图7所示。

图7 模糊推理输出曲面

图7中，e和ec分别表示位移和速度误差，ΔF为模糊推理的输出。从图中可知，模糊推理输出曲面较为平滑，且具有对称性，与设定规则相符，即e和ec同为负时，实际速度和位移小于参考值，给定的电磁力偏小，因此输出的ΔF为正，增大电磁力；e和ec同为正，则同理ΔF为负，减小电磁力。且e和ec的绝对值越大，ΔF的绝对值也越大。当e和ec不同号时，则根据误差绝对值的大小来确定具体确定ΔF的正负和大小。另外，当e和ec同为0时，ΔF也为0，符合设定的规则。

3 仿真和硬件在环测试

3.1 仿真结果

为验证算法的正确性，在Simulink中搭建了系统的仿真模型，仿真模型主要由电源、逆变器、电机、负载、水动力和控制模块几个部分组成，电源为整个系统提供能量，逆变器将输入的直流电逆变为交流电，供给电机，电机动子推动负载加速运动，水动力模块主要模拟水体环境，控制模块主要是包含图2所示的控制算法的实现。整个系统可以模拟直线电机在水体环境下，短时间内推动负载加速运行的工况。电机参数和控制参数如表2所示。

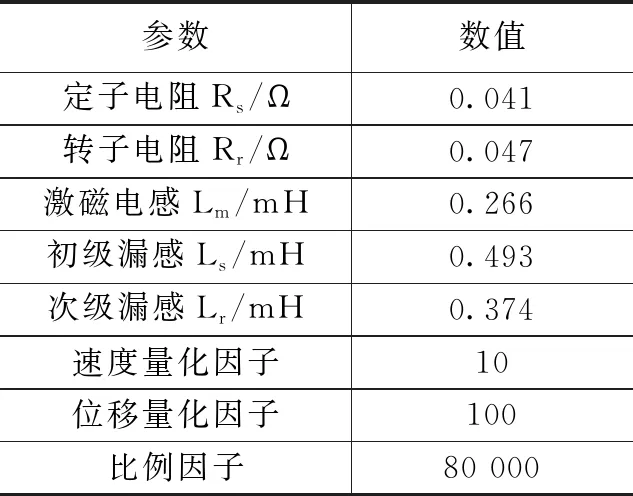
表2 电机参数和控制参数表

为了充分说明算法的有效性，首先给出模糊控制算法投入前，即不加反馈力，命令力直接等于前馈力的情况，之后再投入模糊控制算法，对比模糊控制算法投入前后的速度位移和命令力数据，如图8所示。

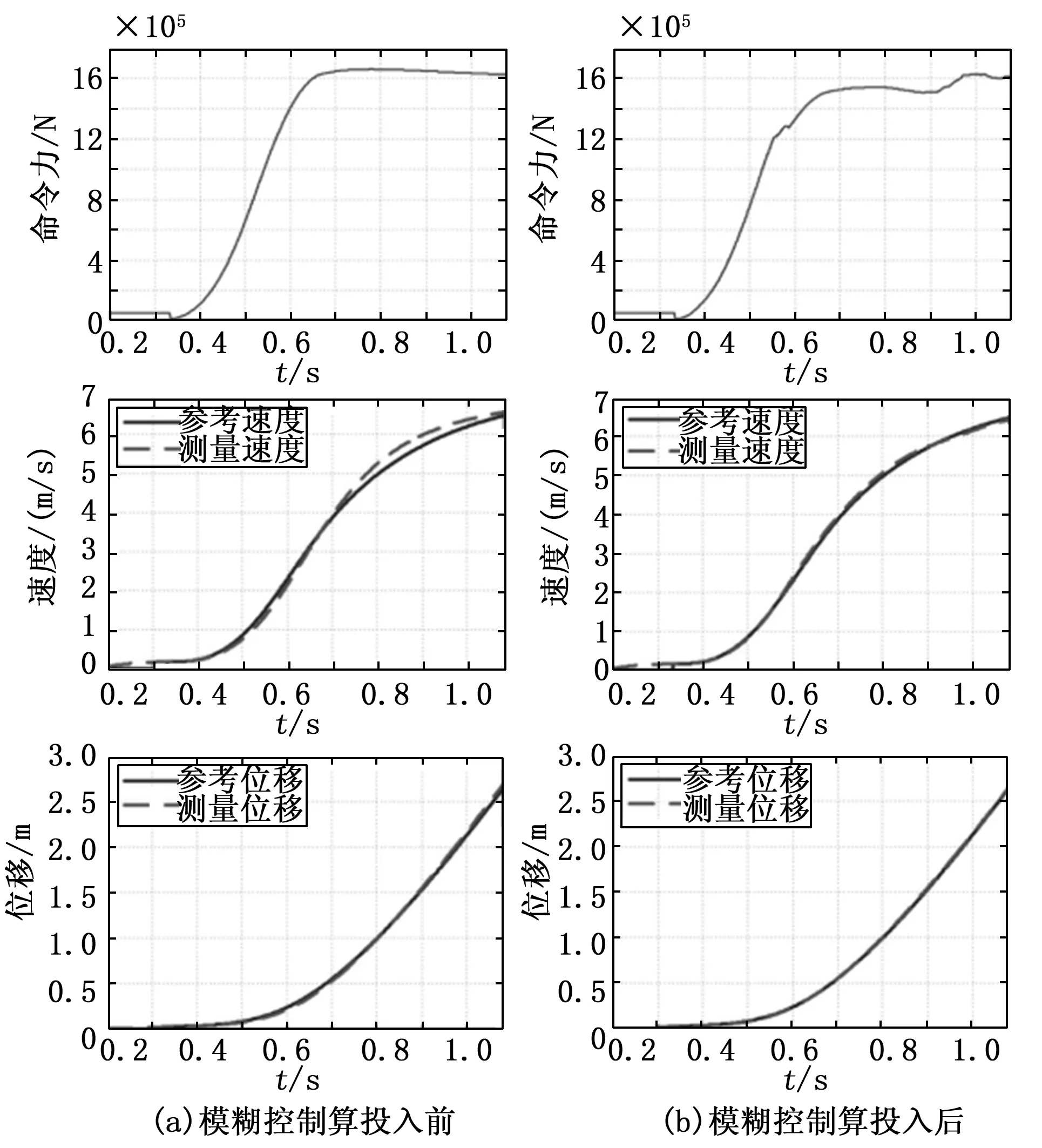
图8 模糊算法投入前后仿真结果对比

从仿真结果可以看出，模糊控制投入前，速度位移跟踪效果较差，电机运行后期，速度明显偏高，速度和位移都有较大的偏差，最大速度误差达到0.296 m/s，位移误差为0.054 m，模糊控制投入后，速度和位移误差大大减小，最大速度误差仅为0.098 m/s，减小了66.7%，最大位移误差仅为0.015 m，减小了72.2%。模糊控制投入后，0.5 s之前，速度位移误差较小，电磁力的调节也较小；在0.5 s之后，误差明显变大，电磁力调节力度也增大，速度和位移误差显著减小。从结果上看，速度和位移已经能够准确的跟踪参考值，且电磁力的调节较为平滑，说明模糊控制算法的有效性。

3.2 硬件在环测试结果

为进一步验证算法的可行性，搭建了半实物仿真平台，如图9所示。

图9 半实物仿真平台

图9中，上位机即带有Labview软件的笔记本电脑，用户可以通过在界面中输入指令和参数，通过串口下发给主控制器，执行不同的运行工况。另外，上位机可以存储主控制器上传的故障和状态数据。主控制器主要包括数字信号处理器(DSP，digital signal processor)芯片以及若干光电转换板，用于将指令和参数通过串口通信同时发送给两个底层控制器，并接收底层控制器上传的故障和状态信息。两个底层控制器和主控制器具有相同的硬件组成，每个底层控制器负责执行一个三相的控制算法，包括图2所示的控制算法、模糊控制算法和相关的故障判定等。算法主要在DSP芯片中执行，由于本文设计的模糊算法计算量小，执行时间较短，不会影响实时控制效果。两个底层控制器通过接口箱与仿真机连接，接口箱包含若干光电转换板，主要用于信号的转换和适配。底层控制器发送IGBT驱动信号到仿真机，同时也采集仿真机中电机模型的位置、电压、电流等状态信号。仿真机包含电机、逆变器和水动力、负载等模型，用来模拟实际的系统运行状态[25]。控制参数仍采用表2中参数，在半实物仿真平台上的测试结果如图10所示。

由图10可知，半实物仿真平台的测试结果与仿真结果基本吻合，模糊控制算法投入前，速度和位移都有较大的偏差，最大速度误差为0.187 m/s，位移误差为0.096 m，模糊控制投入后，速度和位移误差大大减小，最大速度误差仅为0.064 m/s，减小了65.8%，位移误差仅为0.004 m，减小了99.6%，速度和位移能够较好跟踪参考值，且电磁力调节较为平滑，验证了模糊间接矢量控制算法的有效性。

为进一步验证算法的通用性，更改参考速度和位移，并将负载调整为原来的1/2，新工况的硬件在环测试得到结果如图11所示。

由图11可知，工况改变后，前馈力明显偏大，使得速度和位移的误差很大，相比于图10，最大速度误差由0.187 m/s增大到0.281 m/s，位移误差由0.096 m增大到0.183 m，但模糊控制投入后，速度和位移误差显著减小，最大速度误差仅为0.051 m/s，减小了81.6%，相比于图10，最大误差更小，误差减小的比例也更多，而位移误差为0.017 m，减小了90.7%，相比于图10，最大误差稍大，误差减小比例略小，但速度和位移能够准确跟踪参考曲线，电磁力调节稍有波动，但基本平滑，验证了算法的调节能力以及算法的通用性。

4 结束语

本文将模糊控制算法与间接矢量控制结合，用于复杂环境条件下六相直线感应电机的控制，通过将模糊控制算法应用于速度环，避免了对复杂系统建模及PID参数的整定，由于模糊控制仅包含两个输入和一个输出，因此模糊规则较为简单，且调试时仅调节比例因子，能够大幅节省参数整定时间。在模糊控制器设计时，通过对模糊控制规则的优化选取、对隶属函数分区和采用中心法进行清晰化，减小了算法的计算量，确保了实时控制。最后，通过仿真和半实物仿真平台对所提算法验证，结果表明在模糊算法投入后，位移和速度误差减小都超过了65%，速度和位移能够准确的跟踪参考值，且能够适用不同的负载工况，验证了算法的准确性和通用性。后期考虑将该算法应用到实际的装置中。