SiCp/Al 超声椭圆振动车削力热特性仿真研究*

王俊磊，袁松梅，李麒麟，高晓星

（1. 北京航空航天大学，北京 100191；2. 北京市高效绿色数控加工工艺及装备工程技术研究中心，北京 100191）

SiCp/Al 复合材料结合了碳化硅和铝合金两种材料的特性，具有比刚度高、耐磨性高、热膨胀系数低、密度低等优点[1]，在航空航天、武器装备等领域发挥重要作用，并逐渐扩展到电子封装、汽车制造、体育器材等领域，具有广阔的应用前景[2]。但与传统的金属和合金材料相比，硬脆的碳化硅增强颗粒会使其在加工过程中产生严重的刀具磨损、表面缺陷、残余应力等问题[3]。作为研究切削加工的一种便捷、高效的途径，切削有限元仿真具有便于微观切削过程观测、直接获取切削力热数据、节省工件材料等优势。近年来研究人员针对SiCp/Al 进行了大量的仿真和试验研究[4]。

Wang 等[5]通过ABAQUS 有限元仿真软件研究了加工表面缺陷的类型及其形成机理，定量地建立了颗粒尺寸与表面粗糙度之间的关系，发现表面粗糙度接近颗粒半径。Zhou 等[6]针对SiCp/Al 铣削加工进行了仿真及试验研究，认为材料去除包括基体的韧性去除和颗粒的脆性断裂，而表面形貌更依赖于SiC 颗粒去除方式。颗粒的断裂模型主要包括破碎、断裂和拉出，适当提高切削速度可提高加工表面质量。Chinmaya 等[7]在AdvantEdge 和ABAQUS 软件中进行SiCp/Al 有限元切削仿真研究，提出了亚表面损伤与切削力之间的关系模型，该模型建立了损伤深度和切削力之间的关系，损伤深度随切削力的增加而增加。Pramanik 等[8]将SiCp/Al复合材料切削力分解成3 个部分，即对切屑形成力、犁耕力以及颗粒破碎力进行深入研究，建立SiCp/Al 复合材料高置信度切削力预测模型，并通过试验得出切削参数中切削速度和切深对切削力影响变化比较大。Duan等[9]利用ABAQUS 软件建立了SiCp/Al 复合材料切削的有限元模型，通过观测微观切削过程得到了考虑基体附着力、二体磨损和三体滚动影响的三相摩擦力模型，并指出三相摩擦系数随着颗粒体积分数或颗粒尺寸的增大而减小。王泽亮等[10]通过ABAQUS 软件研究了SiCp/Al 切削过程中切削参数对工件温度的影响，发现切削温度随着切削深度增加而增加，随着刀具前角和后角的增大而减小。Davim 等[11]开展了钻削和车削加工的试验，并使用高灵敏度压电式测力仪对试验过程中的切削力进行连续测量，得到了SiCp/Al 复合材料切削力与刀具磨损的关系，得出切削力会随刀具磨损加剧而逐渐增大。Zheng 等[12]发现在超声振动的辅助下，动态断裂韧性的增加使SiC 颗粒断裂和破碎，摩擦系数明显减小，从而降低切削力。Xiang 等[13]通过仿真研究了超声作用下铣削微观形态，发现振动频率越高，颗粒破碎越光滑，裂纹扩展越小，得出适当的超声振幅可以抑制颗粒破碎，进而提高工件的表面质量。Kadivar 等[14]进行了SiCp/Al 复合材料的超声振动钻孔研究，结果表明超声振动辅助钻孔有效降低了钻孔力，孔出口的毛刺更小，表面质量更好。Xiang 等[13]通过试验和仿真相结合的方法研究了超声辅助作用对SiCp/Al 复合材料铣削温度的影响，认为超声振动辅助的应用促进了切屑的流动，降低切屑之间的相互作用，进而降低温度的积累效应，且铣削温度随着振幅的增大而减小。郭东升等[15]通过AdvantEdge FEM 软件研究了超声振动参数对车削力和温度的影响，发现超声车刀振动频率在21 kHz 时最易产生最佳切削效果。何俊等[16]建立了ABAQUS 切削钛合金的力热耦合仿真模型，发现超声振动车削过程中采取较低切削速度可使刀具工件分离更明显，从而降低切削力和切削温度。

综合上述研究，目前国内外对于SiCp/Al 切削力热特性有限元仿真研究主要采用简化的微观建模和等效均质建模，和真实材料差距较大。为了更真实地反映SiCp/Al 车削力热特性，探究超声及车削参数对加工力热行为的影响，优化加工质量，在ABAQUS 中建立了更精确的超声椭圆振动力热耦合车削仿真模型，并开展试验研究，为SiCp/Al 车削加工工艺优化提供理论指导。

1 有限元仿真模型

1.1 有限元几何模型

将三维模型简化为切削平面内的二维模型进行车削仿真研究。对于SiCp/Al 复合材料的有限元几何模型的研究，目前主要是将颗粒简化为球形、阵列或者随机分布在Al 基体内部。这种几何模型相对于匀质的几何模型更准确，但也不能较好地反映真实材料的几何模型。因此，本文通过扫描电镜获得SiCp/Al 真实的金相图，如图1 所示，在样件上选取3 个不同位置进行图像采集，然后对碳化硅颗粒进行分类、测量，统计分析如表1 所示。将碳化硅颗粒看做是多边形，其边数主要分布在3～6 条之间，直径平均值d=30 μm，边长平均值a=24 μm，并对内角进行统计分析。采用Python 语言对ABAQUS 软件进行二次开发，建立了随机多边形颗粒分布的二维几何模型，基于上述对真实材料金相图统计分析的数据，设置该模型中碳化硅颗粒的随机变量参数，如表2 所示，最终得到图2 所示的SiCp/Al 微观几何模型，其与真实的SiCp/Al 更加相近。车削所用刀具为PCD 车刀，其几何尺寸分别为：前角5°、后角10°、刃口半径1.5 μm，刀具二维几何模型如图3 所示。

图1 SiCp/Al 金相图Fig.1 Metallographic diagram of SiCp/Al

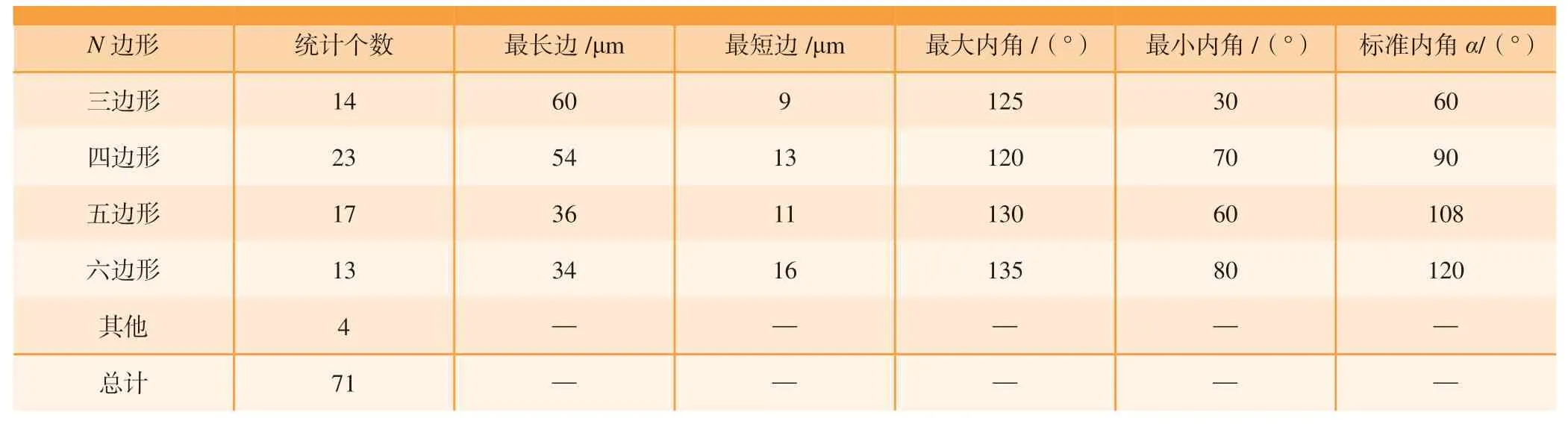
表1 SiC 颗粒形状统计Table 1 Statistical of SiC particle shape

表2 几何模型参数表Table 2 Parameter table of geometric model

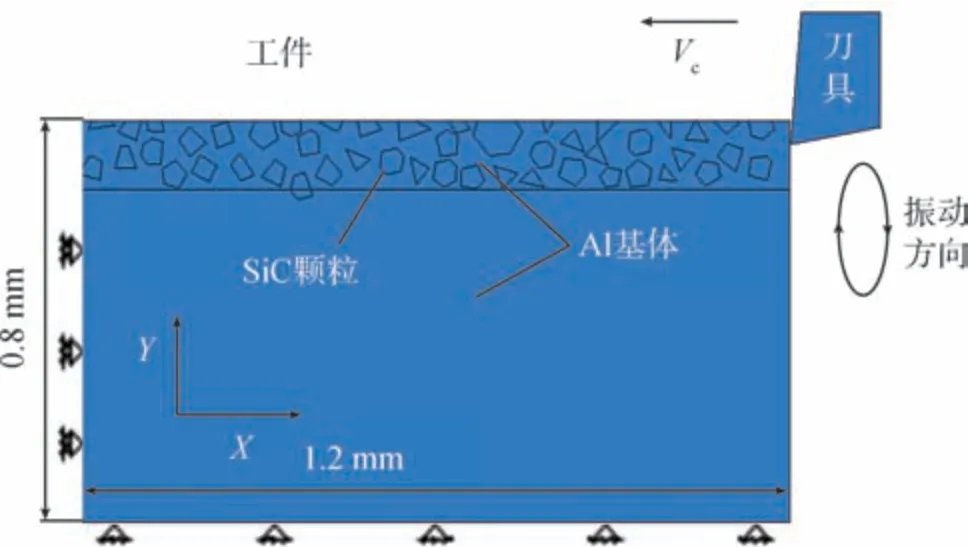
图2 SiCp/Al 仿真几何模型Fig.2 Simulation geometric model of SiCp/Al

图3 PCD 刀具几何模型Fig.3 Geometric model of PCD tool

1.2 仿真模型

1.2.1 材料本构模型

SiCp/Al 材料模型由铝合金基体和碳化硅增强颗粒两部分组成，建模过程中分别赋予材料属性。基体的Al 设置为Johnson-Cook 材料本构模型，其表达式见式（1），方程中等号右边3 项分别表示等效塑性应变、应变率和温度对流动应力的影响，在延性金属的切削仿真中有广泛的应用。SiC 颗粒和Al 基体硬度差别明显，在切削过程中基本不发生变形，因此将其视为线弹性模型，遵循广义胡克定律。

式中，σf为等效应力；A、B、C、n、m 为模型参数；ε 为材料的等效塑性应变；为材料的应变率；为材料的参考应变率；T 为材料的试验温度；Tm为材料的熔点；Tr为室温。

1.2.2 切屑分离准则

在有限元切削仿真过程中，需要设置切屑和工件分离的标准，使切屑和工件实现分离。Al 合金分离准则选取Johnson-Cook 损伤失效准则，该模型对于连续延性切削模型表达更准确，其模型表达式如式（2）所示[9]。

式中，εf为等效塑性变形；D1、D2、D3、D4、D5为材料损伤参数；σ*为应力3 轴度。判断该破坏准则的破坏标准的定义如式（3）所示，当损伤参数D（积累量）累计达到1 时，材料发生破损，相应单元将被删除。

SiC 为硬脆材料，材料断裂准则设置为脆性断裂准则[5]，该准则采用正应力应变法检测颗粒裂纹的萌生，而裂纹扩展的剪切模量定义为裂纹开裂应变的函数，材料破坏则是基于能量准则。

1.2.3 接触属性与边界条件

在SiCp/Al 有限元切削仿真模型中，接触属性主要包括刀具–切屑、基体–颗粒、切屑–工件3 部分。刀具与切屑的接触采用ABAQUS /Explic 中的通用接触，其中切向设置为罚函数法（Penalty algorithms）接触，摩擦系数为0.2[4]，法向设置为硬接触（Hard contact）。目前SiCp/Al 主要通过粉末冶金的方法制备，其界面类型包括轻微反应型界面、干净界面和非晶层界面3 种，其中干净界面占多数，界面层尺寸为纳米级[17]。因此，目前对于SiCp/Al 切削仿真的研究一般是将界面层进行简化[4，6]，基体和颗粒之间采用绑定约束，确保基体和颗粒在界面层的初始位移相同。切屑和工件之间需要施加自接触约束，避免切屑和工件相互穿刺。将工件部分施加固定约束，在刀具上施加超声椭圆运动和切削运动的复合运动，从而实现超声椭圆振动车削仿真。

1.2.4 网格划分

在有限元仿真中，网格数量和质量不仅影响计算结果的准确性，也会影响计算的效率，因此对网格进行优化非常重要。工件网格划分的结果如图4 所示，工件的上半部分为切削区，其几何结构与真实的材料形貌接近，下侧区域为不参与切削的非切削区，直接设置为Al 合金的匀质材料以简化计算过程。工件网格单元的类型为ABAQUS/Explic 中的温度– 位移耦合型，单元属性为四节点减缩积分热力耦合平面应变四边形单元（CPE4RT），双线性沙漏控制求解。对刀具采用单精度分布方式，使靠近刀尖的位置网格细化，从而使其与切削区的网格大小匹配，其余部分采用较大网格。

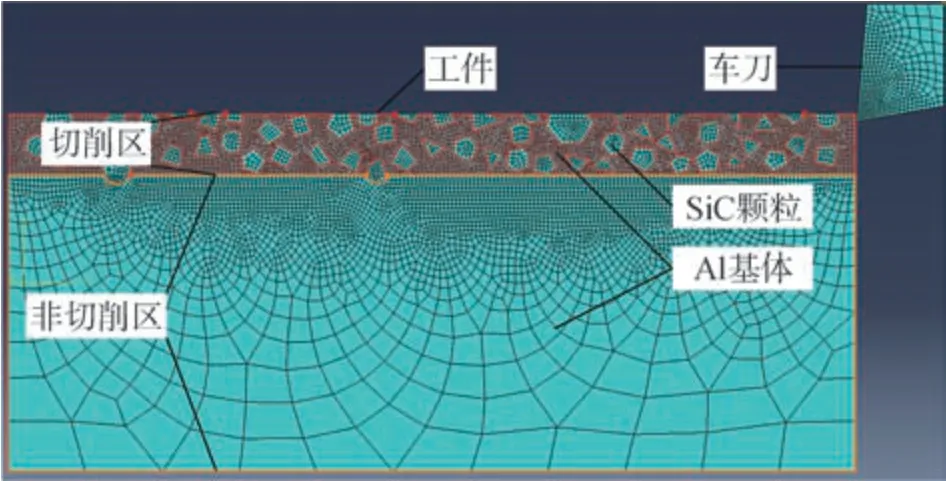
图4 工件及刀具网格划分Fig.4 Mesh generation of workpieces and tool

1.3 材料参数

工件和刀具的基本材料参数如表3 所示，Al 合金材料本构模型参数如表4 所示，Al 合金切屑分离准则模型参数如表5 所示[5，13]。

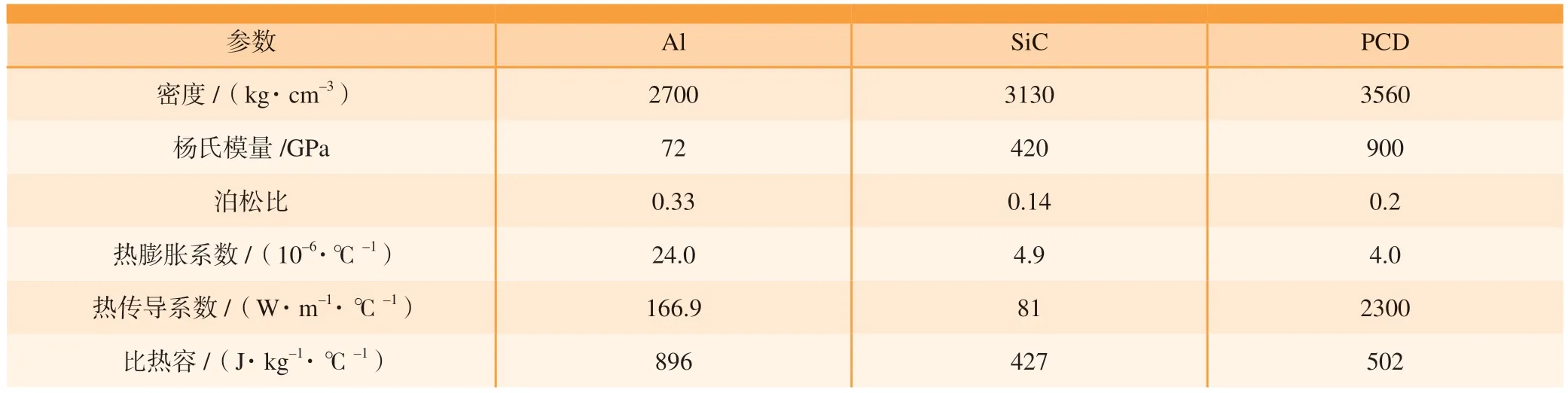
表3 工件和刀具基本材料参数Table 3 Basic material parameters of workpiece and tool

表4 Al 合金的Johnson–Cook 本构模型参数Table 4 Johnson-Cook constitutive model parameters for Al alloy

表5 Al 合金的Johnson–Cook 损伤模型参数[5，13]Table 5 Johnson–Cook damage model parameters for Al alloy[5，13]

2 仿真模型验证及试验方案

2.1 试验条件

为了验证仿真模型的正确性，展开车削验证试验，车削试验现场工作示意图如图5 所示。本研究中试验机床采用美国哈斯TL–1 数控车床进行外圆车削，自研超声椭圆装置与PCD 车刀，如图6 所示，可使刀具在工件的径向和切向产生二维椭圆振动。车削切削力采集采用Kistler 9257B 型台式测力仪，车削加工工件如图7所示。

图5 试验设备及现场设置Fig.5 Experimental equipment and setup of the experimental site

图6 PCD 车削刀具与椭圆超声装备Fig.6 Elliptical ultrasonic equipment and PCD turning tool

图7 车削表面效果Fig.7 Turning surface effect

温度采集所选用的热电偶为Cement-On-K 型超精密薄膜热电偶（OMEGA 公司），车削温度采集点位于金刚石车刀片前刀面上，如图8 所示。基于PCD材料导热系数很大的特点，且测温点距离切削刃仅有2 mm，故认为采集到的温度可较好反映实际切削温度。

图8 车削测温刀具示意图Fig.8 Display of turning temperature measuring tool

2.2 试验方案

本文中刀具的超声椭圆振动轨迹长轴为4 μm，短轴为2 μm，振动频率为40kHz。在已建立的ABAQUS有限元车削模型中针对SiCp/Al 车削表面质量、车削力及车削温度进行仿真试验研究。为研究普通车削中切深变化对力热特性的影响，设计出变切深单因素试验方案，如表6 所示。为了探究切削速度对车削力热特性的影响，设计出变切速试验方案，如表7 所示。

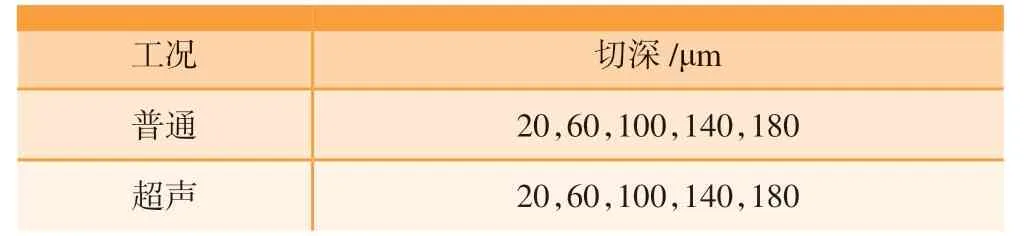
表6 变切深试验方案Table 6 Test scheme of varying cutting depth

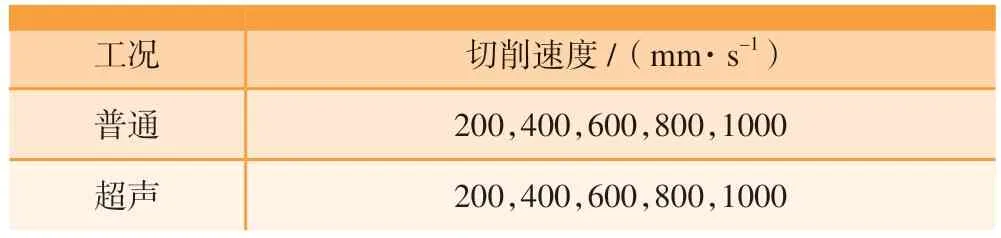
表7 变切削速度试验方案Table 7 Test scheme of varying cutting speed

2.3 仿真结果展示

切削速度600 mm/s、切削深度20 μm 时普通车削仿真应力云图如图9 所示，在SiCp/Al 切削过程中SiC颗粒会受到较大的应力，其中，刀具与其接触点应力最大，为3.749×103MPa。仿真过程中刀具设置为刚体，通过刀具上的特征点导出其受到的支反力，即为车削过程中的切削力，将切削速度600 mm/s、切削深度180 μm车削过程的车刀支反力导出得到切削力，如图10 所示，超声椭圆振动作用下切削力波动较小，且最大值明显低于普通车削，这是由于在普通车削过程中刀具单次将SiC 颗粒去除，但是在超声作用下通过多次微振动锤击将SiC 颗粒去除，因此降低了切削力的波动，并降低最大主切削力。同时在超声椭圆振动下，刀具回撤的过程中切削力还会出现负值。

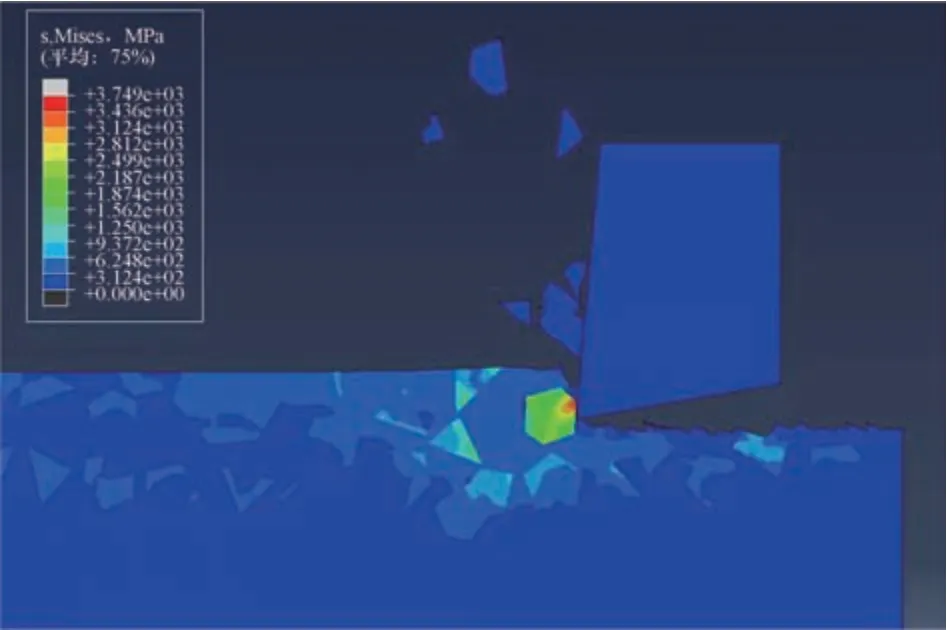
图9 车削仿真应力云图Fig.9 Stress neutrogram of turning simulation

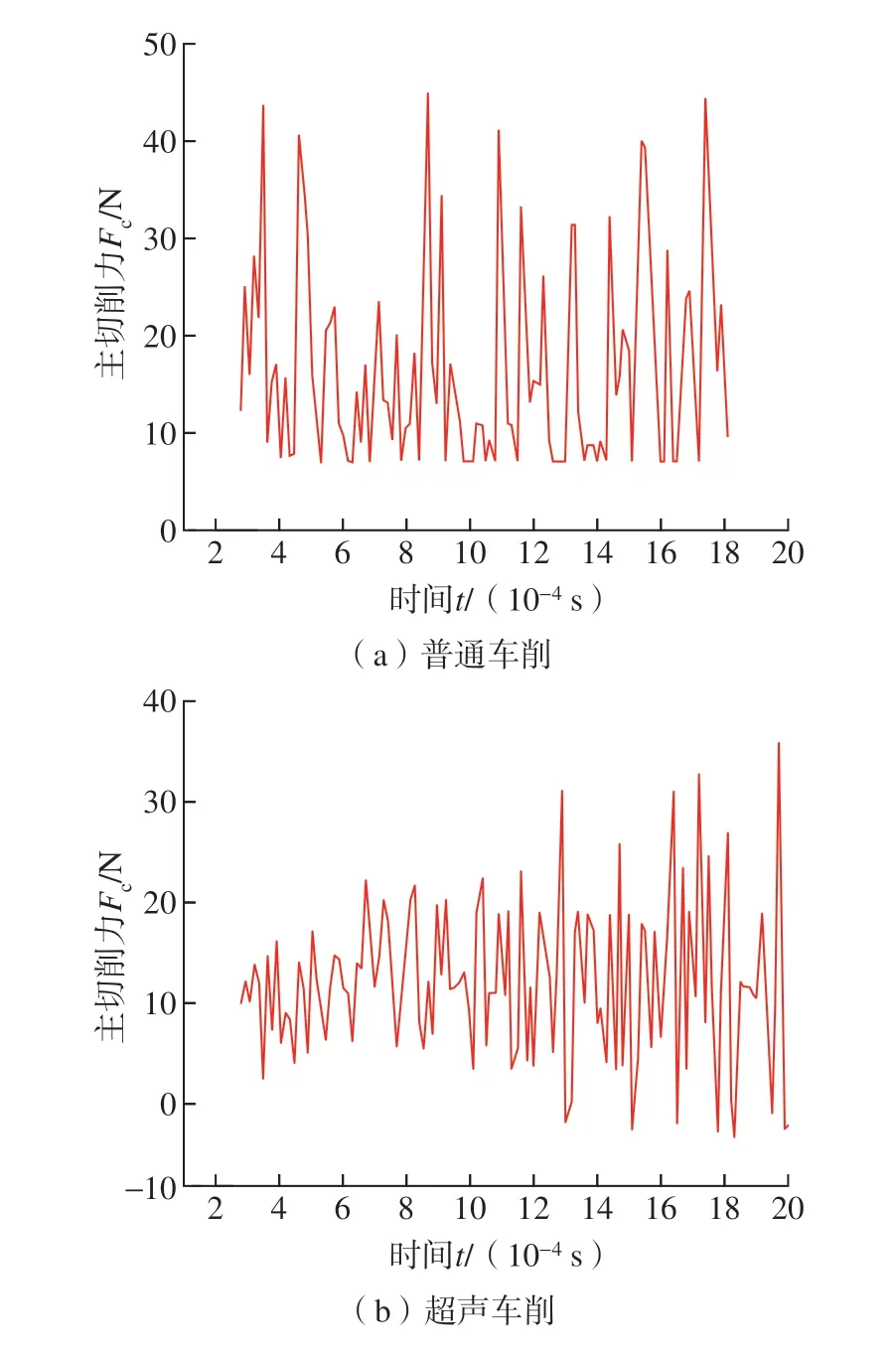
图10 普通与超声振动作用切削力Fig.10 Comparison of cutting forces between normal and ultrasonic elliptic vibration

切削速度600 mm/s、切削深度20 μm 时普通车削温度云图如图11 所示，将切削区温度导出并绘制曲线如图12 所示。室温20 ℃条件下，发现随着车削时间的增加，车削温度随之增加，当散热速率和产热速率达到平衡时温度数值趋于稳定；超声椭圆振动作用下车削温度低于普通车削，这是由于在超声椭圆振动作用下，刀具和工件可断续分离，进而增加散热，降低车削温度。

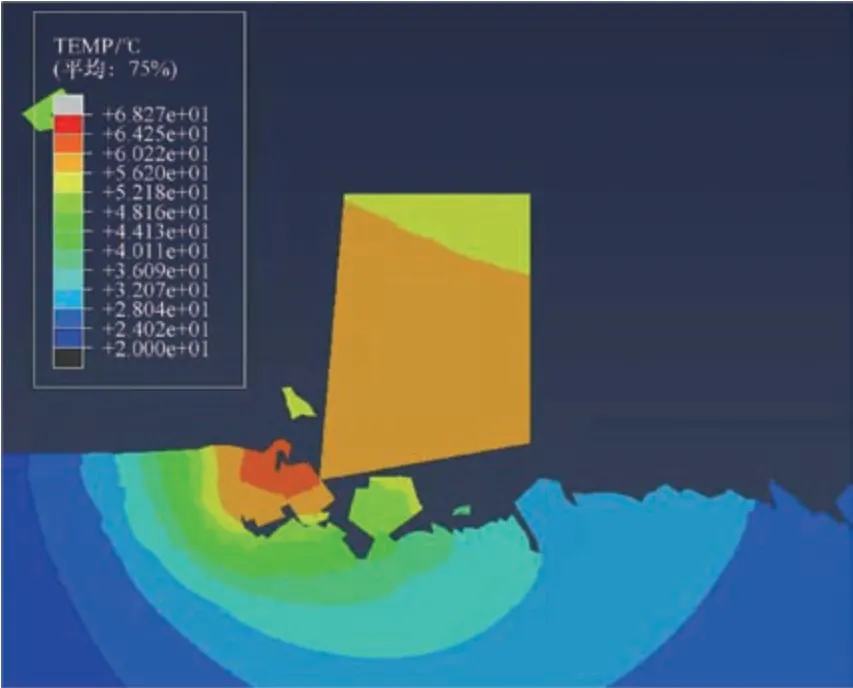
图11 普通车削仿真温度云图Fig.11 Temperature neutrogram of turning simulation

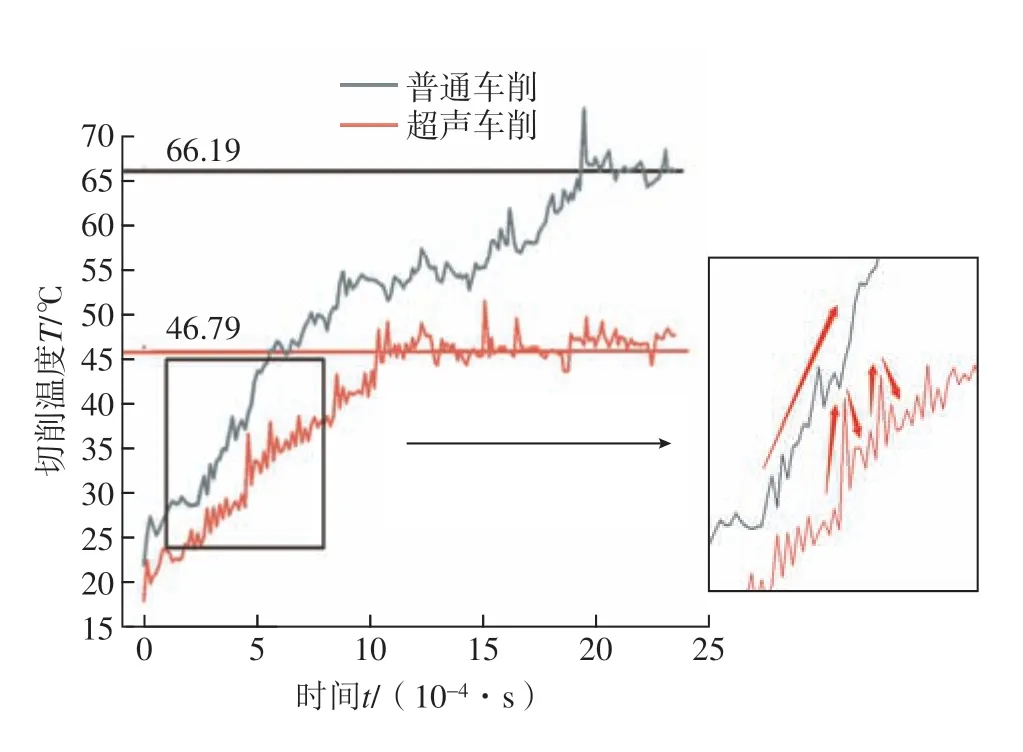
图12 普通与超声振动切削温度Fig.12 Comparison of cutting temperatures between normal and ultrasonic elliptic vibrations

2.4 仿真模型验证

为了验证仿真模型的准确性，针对试验所选工艺参数开展车削试验，对比分析车削力和车削温度与仿真值，获得切削力和切削温度曲线。变切速下仿真与试验主切削力对比如图13 所示。变切深下仿真与试验主切削力对比如图14 所示，车削力仿真与试验最大误差为18.56%。

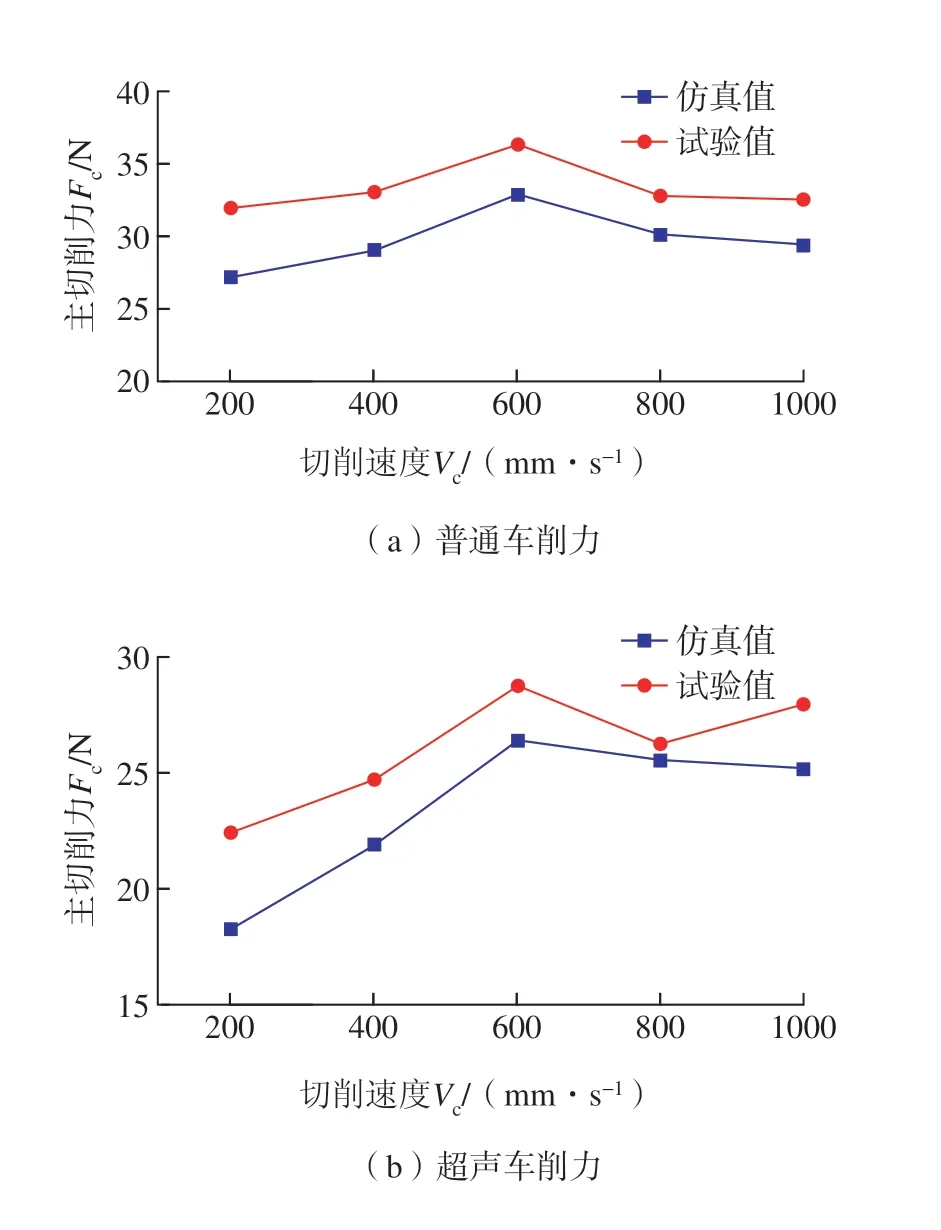
图13 变切速车削力分析Fig.13 Analysis of ordinary and ultrasonic vibration turning force at variable cutting speed

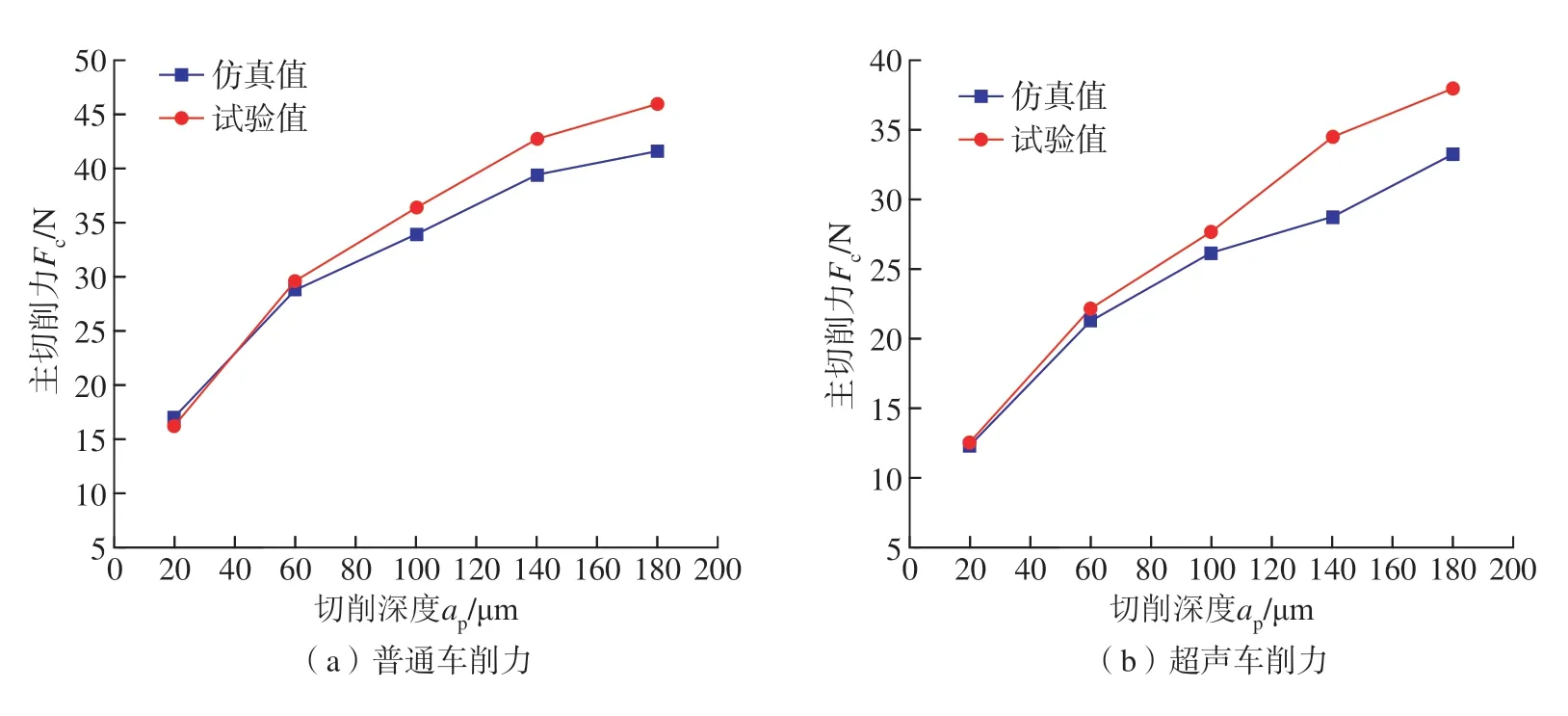
图14 变切深车削力分析Fig.14 Analysis of ordinary and ultrasonic vibration turning force at variable cutting depth

由于车削温度是通过热电偶粘接在车刀前刀面上进行采集的，但是超声设备运行过程中会使刀具发热，超声作用下的温度并不是切削区的温度，因此只对普通车削工况下切削温度的仿真模型进行验证。普通车削工况下，变切速和变切深仿真的切削温度误差分析如图15 所示，车削温度的仿真与试验数值最大误差为16.28%。通过切削力和切削温度的试验验证，说明本研究所建立的有限元仿真模型可以有效反映真实车削过程中切削力和切削温度的趋势。

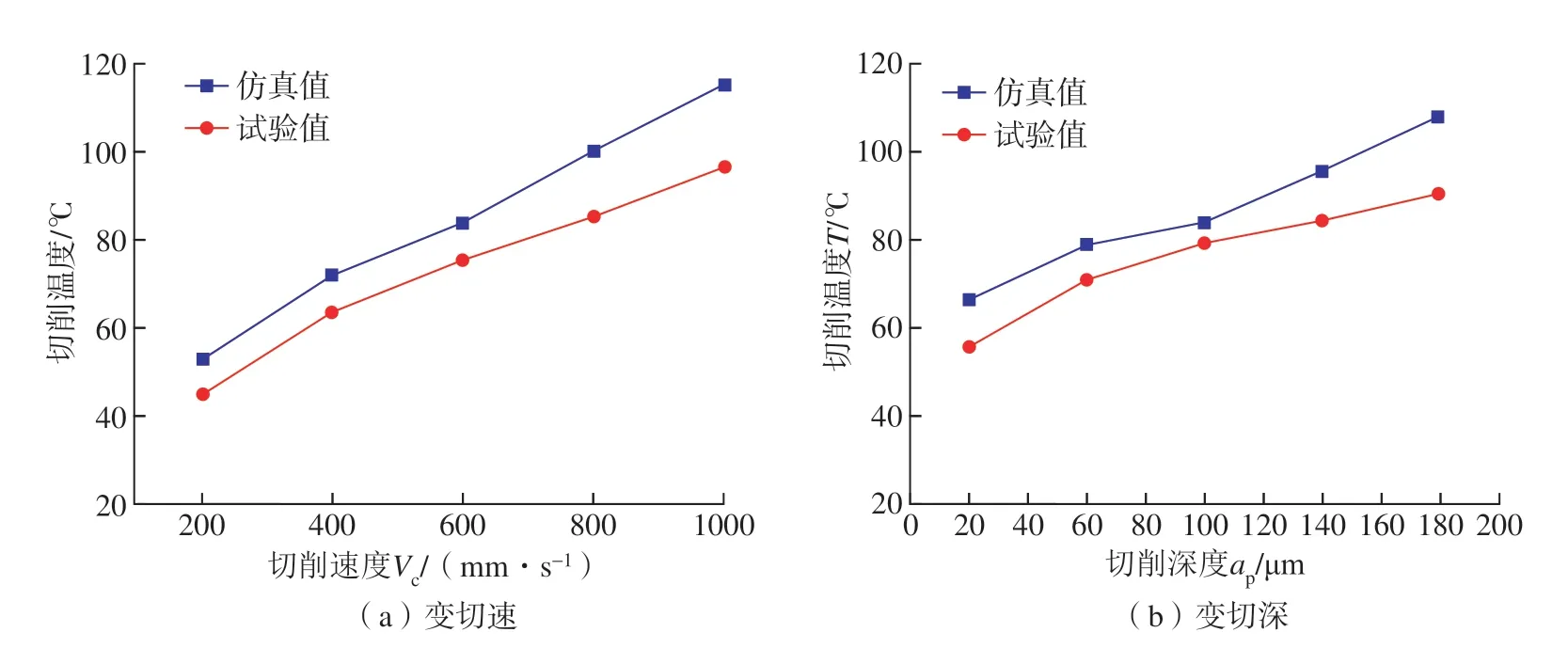
图15 变切速和切深切削温度分析Fig.15 Analysis of ordinary turning temperature at variable cutting speed and depth

3 仿真试验与结果分析

3.1 切削表面质量

在切削速度600 mm/s、切削深度20 μm 的工况下，

普通与超声椭圆振动车削微观表面对比如图16 所示，超声椭圆振动车削获得的表面更平整，对普通车削表面微观形貌进行分析得到其缺陷可分为亚表面损伤、表面裂纹、颗粒耕犁等形式。如图17（a）为瞬时切削力过大造成的SiC 颗粒下方的亚表面损伤；图17（b）为SiC 颗粒与Al 合金未完全脱离进而对颗粒后方的基体产生了挤压破坏，铝合金回弹之后产生表面裂纹；图17（c）为SiC 颗粒未与基体脱离，在刀具推动作用下，SiC颗粒对基体表面产生耕犁破坏。而在超声椭圆振动车削作用下，上述缺陷可有效避免，这是由于在振动作用下材料更容易实现分离，从而使SiC 颗粒更容易从铝合金基体上去除，有效避免进一步对加工表面的破坏。但是当刀具路径上出现过大的SiC 颗粒时，超声振动作用会造成SiC 颗粒破碎，如图17（d）所示，且由于刀具和工件会有断续分离，碎屑未及时排出，进入刀具和工件之间造成进一步表面损伤，因此SiC 颗粒较为均匀，且尺寸较小的SiCp/Al 材料超声椭圆振动车削优势更显著。

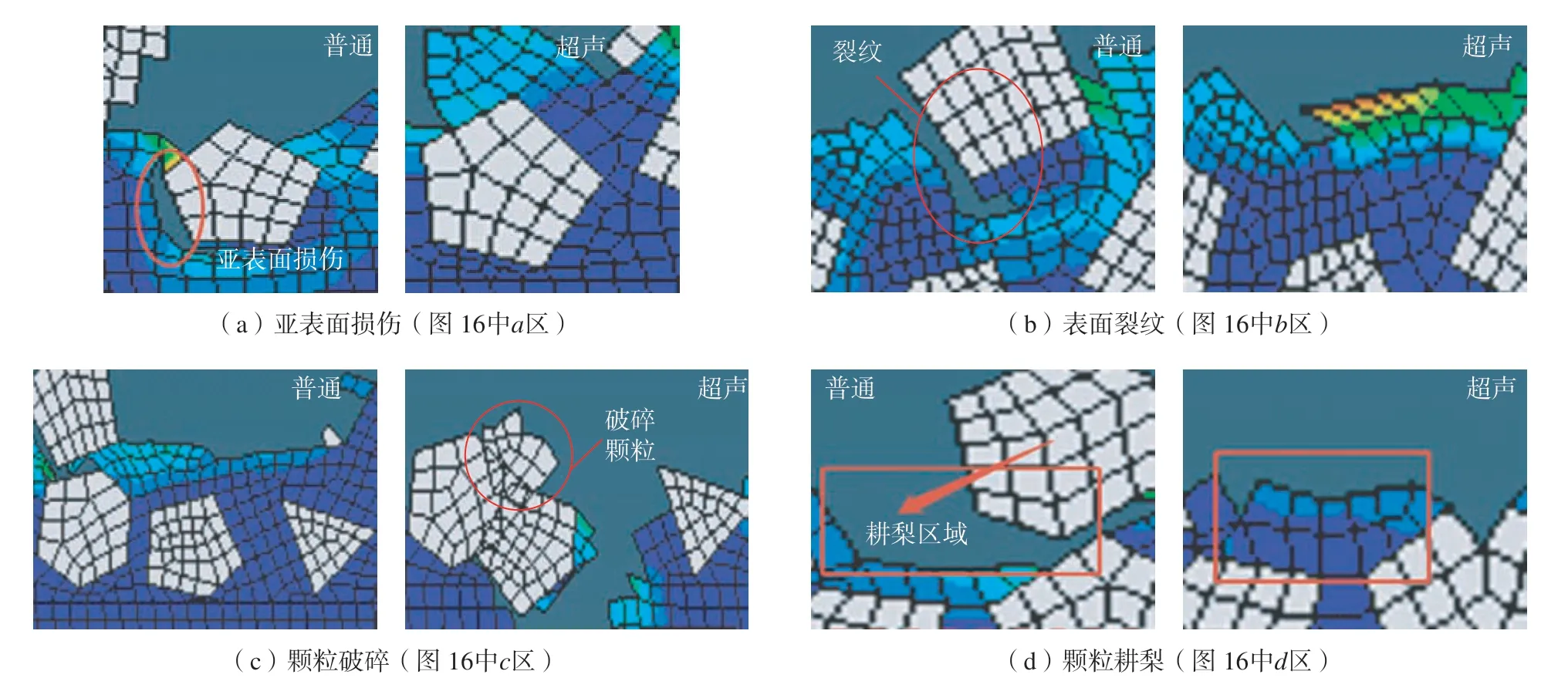
图17 表面缺陷微观图Fig.17 Micrograph of surface defect

3.2 切削力

图18 为不同切削速度对最大主切削力的影响曲线，切削深度设定为100 μm，切削速度为200～1000 mm/s，普通和超声车削最大主切削力随着切削速度增加呈先增加后减小趋势，在Vc=600 mm/s 时达到最大，分别为32.88 N 和26.27 N。在Vc=200 mm/s 时超声作用相对于普通车削作用最显著，将切削力降低了33.17%。图19 为切削深度对主切削力的影响，该组试验将切削速度设定为600 mm/s，切削深度为20～180 μm，研究不同切削深度对最大主切削力的影响。该组试验结果表明，普通和超声车削的最大主切削力随切削深度增加的变化趋势一致，超声振动作用显著降低了主切削力，在ap=20 μm 时超声作用最显著，切削力降低27.35%。

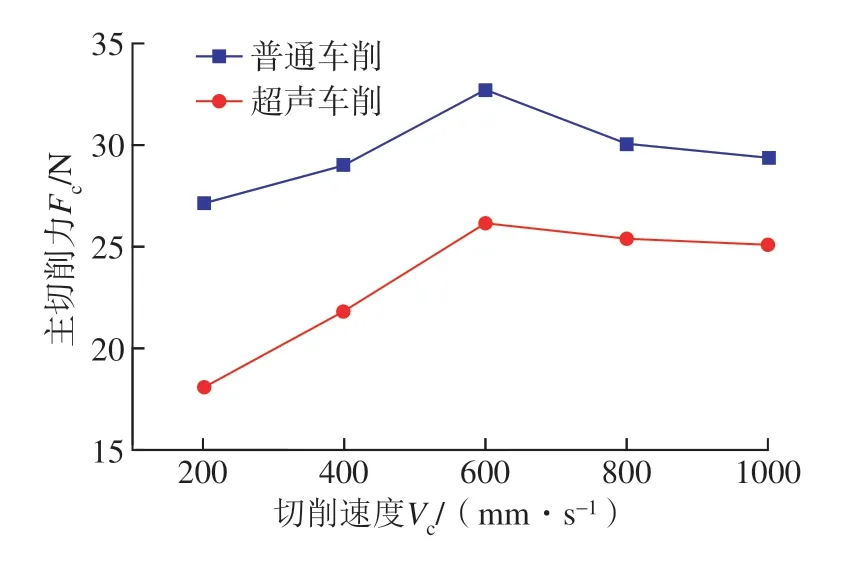
图18 切削速度对切削力的影响Fig.18 Influence of cutting speed on cutting force

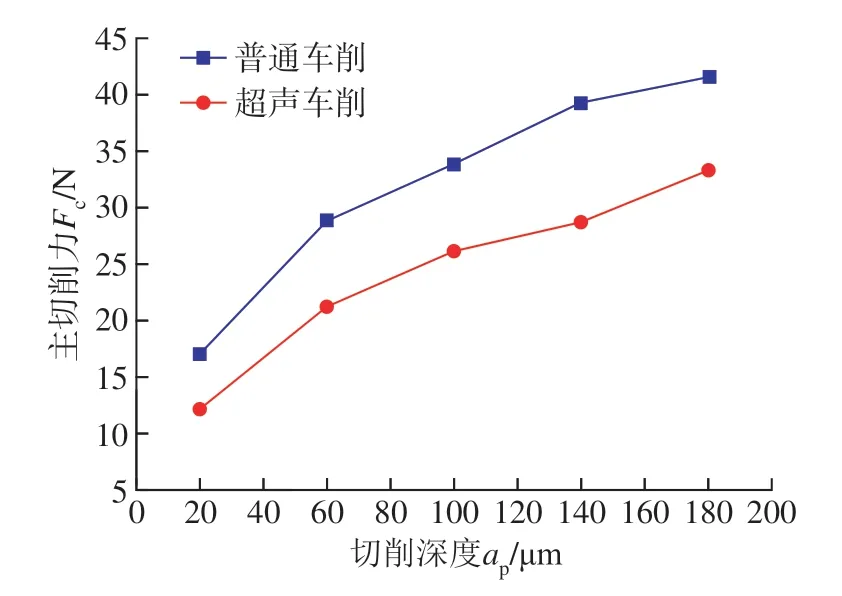
图19 切削深度对切削力的影响Fig.19 Influence of cutting depth on cutting force

3.3 切削温度

图20 为切削速度对切削温度的影响关系，选择切削深度为100 μm，切削速度为200～1000 mm/s，普通车削温度最高为115.29 ℃，超声振动车削最高温度为95.23℃，超声作用可有效降低切削温度，且在Vc=200 mm/s 时减温效果最明显，可将切削区温度降低22.62%。图21 为切削深度对切削温度的影响，切削速度为定值Vc=600 mm/s，随着切削深度的增加，普通和超声车削温度均有增加的趋势，超声振动作用可显著抑制切削温度的升高，在ap=20 μm 时，切削温度降低29.31%。

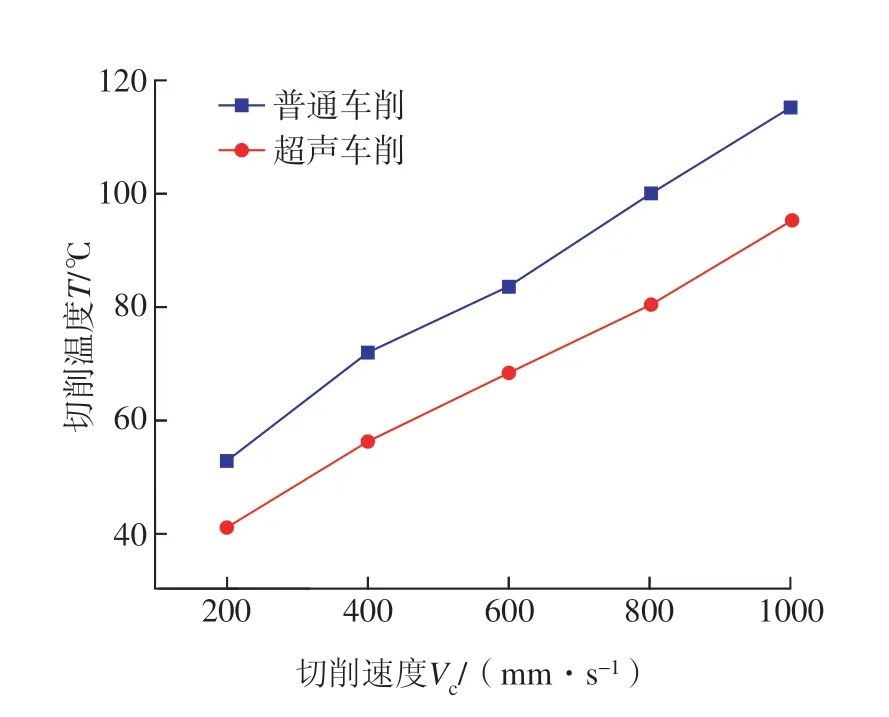
图20 切削速度对切削温度的影响Fig.20 Influence of cutting speed on cutting temperature

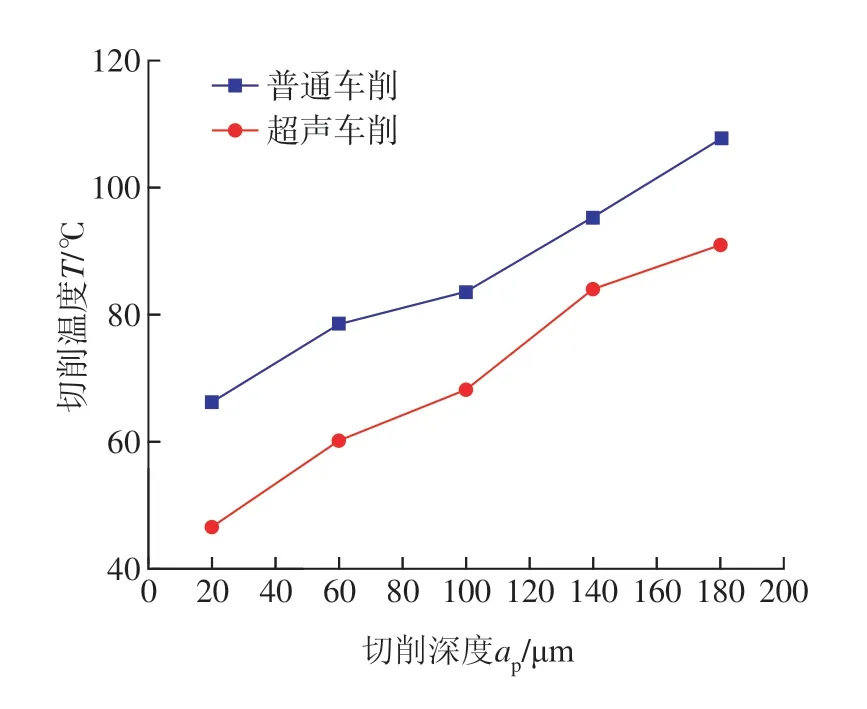
图21 切削深度对切削温度的影响Fig.21 Influence of cutting depth on cutting temperature

4 结论

本文建立了SiCp/Al 复合材料超声椭圆振动车削有限元力热耦合仿真模型，并针对切削表面质量、切削力热特性展开车削仿真试验研究，最终获得了车削速度、车削深度与车削力热之间的影响关系，为SiCp/Al 高精度车削加工提供理论依据，本文的结论如下：

（1）在ABAQUS 仿真软件中建立了多边形颗粒随机分布的模型，并在此基础上获得更接近实际情况的有限元切削仿真模型，通过试验进行验证得到主切削力和切削温度误差在18.56%以内。

（2）对有限元车削仿真微观表面进行分析，发现超声椭圆振动车削可有效降低SiCp/Al 车削过程中亚表面损伤、表面裂纹等的损伤产生。

（3）超声椭圆振动作用可有效降低SiCp/Al 车削中主切削力和切削温度，在ap=100 μm，Vc=200 mm/s 时超声作用降低切削力作用最显著，达到33.17%；在ap=20 μm，Vc=600 mm/s 时超声作用降低切削温度作用最显著，达到29.31%。