基于改进PID算法横列式双旋翼无人机系统

陈文娟,潘乾曜,苏世达,宋瑛麒,曹佳音,徐志杰,王玉斗

(中国石油大学(华东) 理学院,山东 青岛 266580)

旋翼无人机是目前人工智能领域的一个重要分支。目前市面上常见的多旋翼无人机旋翼固定,无法实现推力矢量的控制。随着无人机飞行任务的复杂化,对于无人机机动性以及续航能力的要求日益提升。横列式双旋翼无人机作为一种新型无人机机型,其两组旋翼左右对称,彼此螺旋桨转向相反,旋翼扭矩力可以相互抵消,具有较强的控制灵活性与续航能力[1],能够弥补固定旋翼无人机机动性能上的不足。

国内外近些年针对横列式双旋翼无人机的研究也取得了许多进展,2012年美国麻省理工学院Markus Ryll团队最早提出倾转旋翼这一设计结构[2],其主要研究的方向为该新型独立可倾转四旋翼无人机在螺旋桨倾转方向可控之后对无人机六个自由度的完全驱动[3];Fernandes团队提出一种在同轴的两个旋翼上增加2自由度倾转机构,另两个电机保持固定的倾转旋翼无人机方案[4];国内杜玉虎团队研制了一种倾转旋翼与固定翼结合的小型无人机[5];杨立本研究团队针对横列式双旋翼无人机开发了ADRC姿态控制算法,增强了其抗干扰性[6];马逸君、战强团队完成了一种新型横列双旋翼无人机的设计并实现了仿真运行[7]。

根据上述调研,相关研究均没有考虑传感器测量误差对于横列式双旋翼无人机控制精度的影响,且目前所使用的传统PID算法无法消除三轴加速度计测量误差[8]。同时现阶段的研究缺乏一套完整的试验样机+测控地面站系统。针对上述问题,本文创新性开发了一种基于三轴加速度计误差补偿算法与闭环PID控制算法相结合的改进串级双闭环PID算法,相比于传统闭环PID算法可以有效抑制三轴加速度计测量值误差以提高无人机的控制精度,基于此在Simulink环境下进行了飞行控制仿真;随后搭建了试验样机并开发了测控地面站系统;最终完成了试验样机空中悬停实验。仿真与实际实验结果验证了改进算法控制系统在理论与实际环境下的优势与可执行性。

1 系统动力学模型建立

首先建立如图1所示的坐标系,(x0,y0,z0)(x,y,z)(x1,y1,z1)(x2,y2,z2)分别为惯性坐标系、机体坐标系、左旋翼坐标系与右旋翼坐标系。

图1 无人机相关坐标系定义

(1)

为方便表述,式1中sin与cos均使用s、c表示。其中φ为横滚角,θ为俯仰角,ψ为偏航角。

根据图1分析可知,横列式双旋翼无人机通过同时改变同列电机转速来产生垂直上下运动;当电机同速旋转时,通过旋翼倾转舵机的同向倾转来产生俯仰运动;当旋翼倾转舵机倾转角度同时为0,通过调节无人机左右电机的转速差来实现滚转运动;最后通过旋翼倾转舵机的反向同角度倾转以实现偏航运动。

根据牛顿-欧拉定理,可以推导出横列式双旋翼无人机的六自由度非线性动力学方程:式中输入参数U1-U4分别满足式2和式3。

(2)

(3)

其中,U1-U4是旋翼沿着不同轴线方向的升力;KT是旋翼螺旋桨的推力系数;ω1、ω2与δ1、δ2分别为同列2个螺旋桨的转速与2个倾转舵机产生的倾转角度。

横列式双旋翼无人机实际物理参数经整定如表1所示。

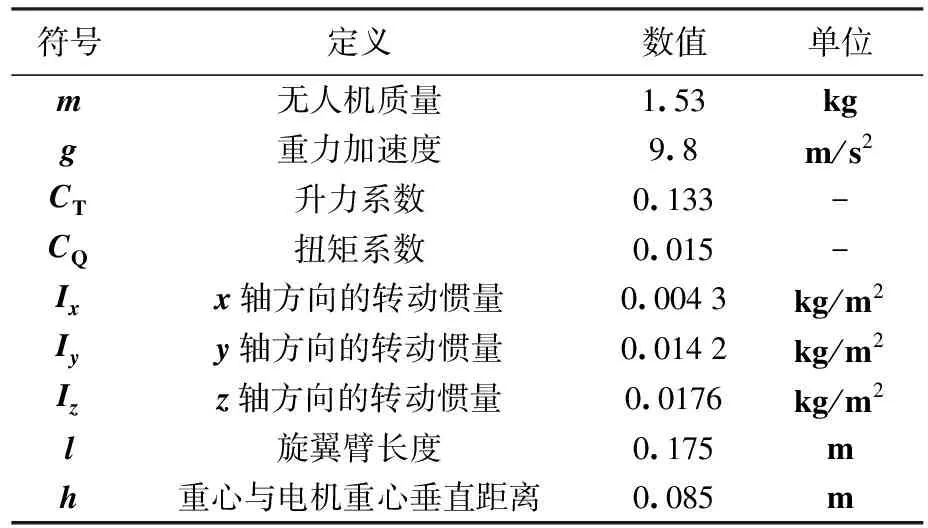
表1 实际物理参数

2 系统控制算法设计与仿真

2.1 控制系统设计流程

控制系统工作流程如图2所示,控制系统设计包括MCU初始化、姿态解算、控制信号读取与飞行姿态控制四部分,其中飞行姿态控制是控制系统设计的重点与难点。

图2 横列式双旋翼控制软件工作流程

(1)MCU初始化:初始化寄存器,包括对三轴加速度计、气压高度传感器与陀螺仪芯片进行程序覆写初始化操作。

(2)姿态解算:根据IMU数据利用四元数法表示出三轴坐标旋转矩阵,将得到的三轴旋转矩阵相乘以实时更新无人机姿态矩阵,最后将姿态矩阵转化为三轴欧拉角,求解出飞行器的实际姿态角。

(3)控制信号读取:利用中断处理算法输入捕捉中断以实现遥控器控制信号的读取,利用串口中断算法实现与地面站之间数据的收发,以完成遥控器、地面站以及导航解算所给定控制信号的读取。

(4)飞行姿态控制:包括改进串级双闭环PID控制算法与PWM信号输出2部分,改进串级双闭环PID控制算法设计将在下一小节具体介绍;通过PID控制器输出的PWM信号会根据其占空比实现对电机转速与舵机倾转角度的控制。

2.2 改进串级双闭环PID控制算法设计

2.2.1 算法整体结构框架设计

本文设计的改进串级双闭环PID算法创新性将自主开发的三轴加速度误差补偿算法与闭环PID控制算法相结合,解决了传统闭环PID算法无法实现三轴加速度计观测误差补偿的问题,该算法的整体结构框图如图3所示。

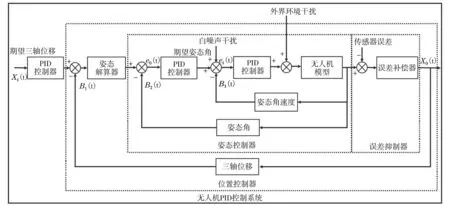
图3 改进串级双闭环PID算法结构框图

2.2.2 三轴加速度误差补偿算法设计

三轴加速度计是无人机惯导的关键部件,其输出精度直接影响无人机飞行控制的精度。因为加工工艺的限制,本文所使用的MPU6000三轴加速度计难免会产生三轴不正交误差。三轴不正交误差指的是加速度计三个敏感轴会偏离理想正交系微小的角度,从而产生加速度测量值的非线性误差。

针对这一问题,首先对三轴加速度计的误差进行数学建模[9],如式(4)所示。由于该款三轴加速度计在生产过程中已经校准了零位偏移误差,所以在模型中可以不用考虑零位偏移误差的影响。

(4)

式(4)中ax、ay、az为三轴加速度计实际测量值;axT、ayT、azT为三轴加速度计真实值;矩阵Eij为灵敏度与非正交误差系数矩阵;矩阵ej为随机误差;α、β、γ分别为3个敏感轴偏离理想正交系的角度。

根据上述模型,本文采用基于最大似然法的椭球拟合算法[10]来搭建误差补偿器。对式10进行变形,可以得到三轴加速度计误差补偿模型[10]:

(5)

式(5)中esum_x、esum_y、esum_z为修正后的随机误差系数,图4为误差补偿器的系统流程框图。

图4 三轴加速度计误差补偿系统框图

以无人机静止于水平面为例,取保持静止姿态1s内三轴加速度计的数据作为1组样本,取100组数据样本,在误差补偿器中进行迭代,得到如表2所示无人机静止条件下M与esum的参数值。

表2 无人机静止条件下误差补偿器参数

2.2.3 闭环PID控制算法设计

闭环PID控制器采用增量式PID控制:

(6)

(7)

其中ev与ew分别等于vdes-v与ωdes-ω,通过上述公式可以分别得出横列式双旋翼矢量无人机的期望升力与期望旋转力矩,再通过控制分配得出2个旋翼电机的期望转速与2个倾转舵机的期望倾转角度,控制分配公式如下:

(8)

(9)

(10)

(11)

2.3 控制系统Simulink仿真

基于上述理论分析,在所建立的横列式双旋翼无人机动力学模型中加入改进串级双闭环PID控制算法对控制器进行阶跃输入,并根据对应的阶跃响应曲线进行PID参数的整定,如图5所示。

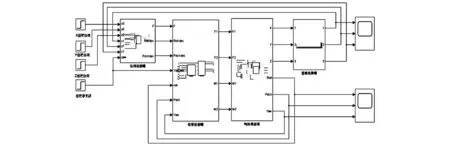
图5 仿真系统Simulink框图

该仿真系统包括:位置控制器、姿态控制器、横列式双旋翼无人机数学模型与误差补偿器四部分。输入为4个阶跃控制信号,自上而下分别为期望三轴xyz位置信号与期望偏航角信号。四个模块功能如下:

(1)位置控制模块:将输入的三轴位置信号与偏航角信号利用四元数转换法转化成期望升力、期望俯仰角与期望滚转角信号并输入姿态控制模块进行下一步运算。

(2)姿态控制模块:利用牛顿-欧拉定理将从位置控制器输出的期望升力、俯仰角与滚转角信号进行姿态解算,输出同轴2个旋翼的升力与2个旋翼螺旋桨的旋转力矩。

(3)无人机数学模型:将从角度控制器输出的升力与旋转力矩导入动力学模型中,解算出无人机的实际位置与姿态角信号并反馈给上述2个模块进行调整。

(4)误差补偿模块:对模拟观测三轴位移参数的累积误差进行补偿与消除。

图6为改进PID算法与传统PID算法仿真结果对比图。初始输入阶跃模拟信号为:x0=25,y0=12,z0=30,yaw_des=0.5;初始设置观测误差为:y轴方向0.4°。红色实线为改进串级双闭环PID算法响应曲线,蓝色虚线为传统PID算法响应曲线。

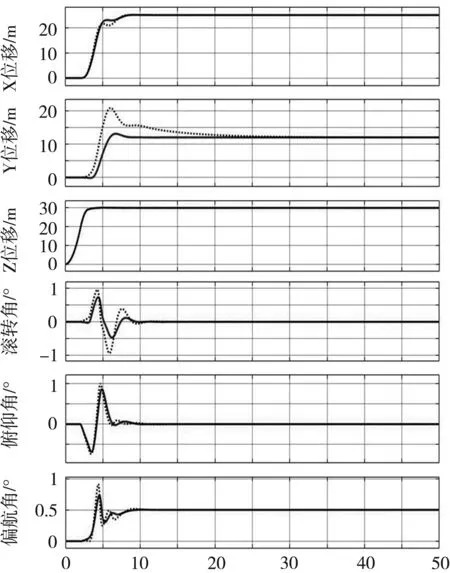
时间/s

据图分析,经过30次仿真实验可得出相关结论:改进串级双闭环PID算法对于y轴位移以及3轴姿态角控制的超调量同比减少了约78%、26%、19%与44%。仿真结果说明相较于传统串级双闭环PID算法,改进串级双闭环PID算法有效地提升了系统的控制性能,具有更强的误差抑制能力。

3 试验样机设计与实验

3.1 试验样机系统总体设计

横列式双旋翼无人机由5个分系统组合而成,即飞行主控系统、传感器系统、控制执行系统、信号收发系统与电源稳压系统。试验样机系统硬件总体结构如图7所示。

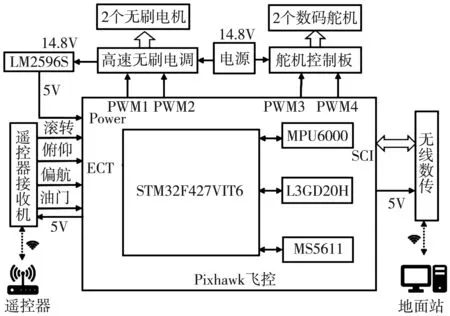
图7 试验样机系统总体硬件结构

(1)飞行主控系统采用基于PX4的32位开源飞控Pixhawk。该飞控以STM32F427VIT6(168MHz,256KB,ROM/2MB闪存,100Pin)为中央处理器,主要负责传感器误差补偿与无人机姿态角与飞行高度的解算;结合遥控器接收机(FS-IA10B)的控制信号实时控制同列2个旋翼电机转速与2个倾转舵机倾转角度;结合无线数传完成与无人机地面站数据的双向交互[11-13]。

(2)传感器系统包括MPU6000三轴加速度计、L3GD20H陀螺仪芯片与MS5611气压计,主要负责测量角加速度、线加速度与海拔高度等姿态信息的测量与反馈[14]。

(3)控制执行系统包括动力系统与旋翼倾转系统。其中动力系统选用1对大疆2312A无刷电机与好盈40A电子调速器,分别安装1对9 450自锁正反桨提供动力。倾转舵机采用JX1109数码舵机,该舵最大扭力为1.7kg/cm[15-16]。

(4)信号收发系统包括FS-IA10B接收机与ESP8266Wi-Fi无线数传,主要负责主控系统与遥控器和地面站数据信号的双向交互。

(5)电源稳压系统采用LM2596S可调降压模块,主要负责将14.8V直流电源电压降低到5V以供给主控系统使用,如图8所示。

图8 横列式双旋翼无人机实物图

3.2 测控地面站软件开发

测控地面站软件采用UE4引擎作为开发平台,主要作用在于实现空中悬停实验数据的采集与可视化。图9为测控地面站系统操作界面。该系统可以实时动态显示不同型号无人机的三维空间姿态角与高度变化、旋翼螺旋桨运行状态与虚拟第一人称视角。

图9 地面站操作主界面

3.3 试验样机空中悬停实验

图10为进行中的试验样机空中悬停实验。完成了改进PID算法与传统PID算法试验样机悬停对比实验。对比实验指定悬停高度均为4m,一共进行了10组对比实验。

图10 试验样机空中悬停实验

表3、表4分别为10组空中悬停对比实验测量数据平均值。表5为姿态角数据分析结果,表6为实验误差分析。图11为对比实验姿态数据时域曲线,其中实线为改进串级双闭环PID算法,虚线为传统PID算法。

表3 基于改进PID算法试验样机实验数据记录

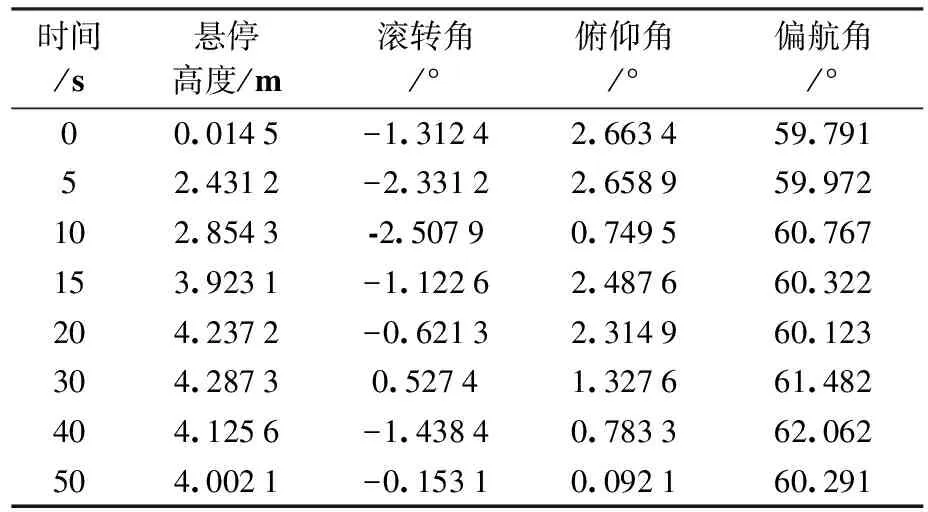
表4 基于传统PID算法试验样机实验数据记录

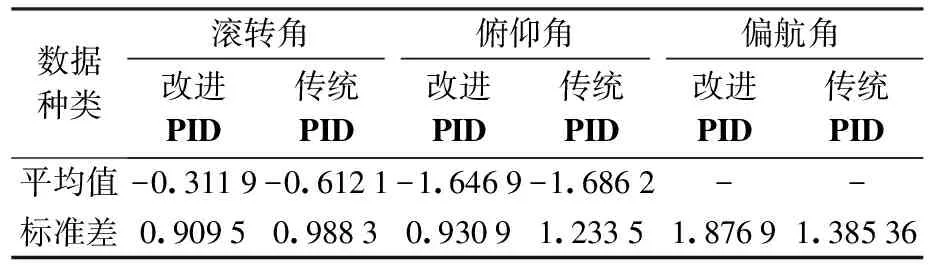
表5 对比实验姿态角数据

表6 对比实验误差

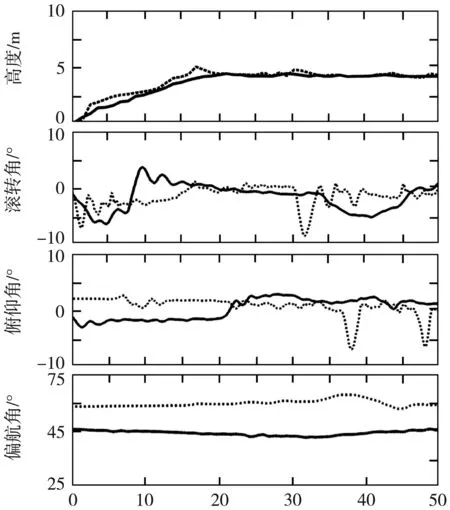
时间/s

对无人机高度数据分析可知,前20 s无人机处于上升状态,20 s后稳定在设定高度。据图11所示,改进串级双闭环PID算法相较于传统PID算法能更好地抑制高度位移的振荡。

据表5分析可知,基于改进PID算法试验样机稳定悬停时滚转角与俯仰角的平均值相比于传统PID算法更接近于0,且标准差同比减小了7.9%与23.8%。说明改进PID算法具有更强的姿态角控制稳定性,在一定程度上提升了横列式双旋翼无人机的控制精度。

据表6分析可知,基于改进PID算法试验样机悬停高度、滚转角、俯仰角与偏航角的稳态误差较传统PID算法同比减少了35.68%、49.04%、2.33%与55.96%,说明改进PID算法具有更高的控制精度。

4 结 论

本文创新性将自主开发的三轴加速度计误差补偿算法与闭环PID控制算法相结合,设计出一种基于改进串级双闭环PID算法的横列式双旋翼无人机。本文首先介绍了动力学模型的搭建与物理参数的整定;其次阐述了控制系统与改进串级双闭环PID算法的设计并利用Simulink软件仿真验证了该系统的理论稳定性;再者完成了试验样机+测控地面站系统的搭建并完成了空中悬停实验。实验结果表明,相较于传统闭环PID算法,改进串级双闭环PID控制算法对于横列式双旋翼无人机具有更好的控制稳定性,基本实现了对机体飞行姿态的自稳定控制与误差补偿。后续还可以引入相关机器学习算法实现对超调量与调节时间的减少与缩短。