考虑尺度敏感性的长江中下游暖区暴雨初始扰动方案比较分析

徐渊，闵锦忠，庄潇然

(1.南京信息工程大学气象灾害教育部重点实验室/气象灾害预报预警与评估协同创新中心，江苏 南京 210044；2.江苏省气象台，江苏 南京 210008)

1 引 言

高分辨率数值模式是预报强天气的有力工具，但由于初值、模式和大气系统内部的混沌特性，给模式的预报带来较大的不确定性[1-2]。在大气预报不确定性的基础上，Epstein[3]和Leith[4]引入了集合预报的思想，通过使用多个包含扰动、并行积分的成员来表征预报不确定性，从而将随机论引入到数值预报中。半个世纪以来，集合技术从最初的全球数值预报扩展到高分辨率的区域数值预报，成为数值预报业务的一个关注热点[5]。

数值预报的积分求解高度依赖于初值，气象学家最早依据初值不确定性来构建集合。早期的Monte Carlo 随机扰动法[4]、时间滞后平均法[6]和观测扰动法[7]通过估计分析误差的概率分布来产生初值扰动，但这类方法没有考虑误差的动力学增长特征，因而在斜压不稳定区域离散度难以增长。随后发展的扰动方法则基于快速增长模的思想，着眼于沿预报系统误差增长最快的方向来扰动初始条件，取得了较多成果，主要包括增长模繁殖法（Breeding of the Growing Mode，BGM）、奇异向量法、集合变换法、集合变换卡尔曼滤波（Ensemble Transform Kalman Filter，ETKF）和集合资料同化（如集合卡尔曼滤波）等[8-10]，上述方法从全球集合预报一直沿用到区域高分辨率乃至对流尺度集合预报系统的构建中。除初始扰动外，模式物理扰动和侧边界扰动也受到广泛关注[11-12]。尽管如此，由于初始扰动能够比模式和侧边界扰动更早产生较大离差，同时初始扰动的影响也依赖于模拟域的大小，因而在区域对流尺度集合预报中初值仍是相当特殊且重要的不确定性来源[13-15]。

区域集合预报初值扰动的构建包括三个主流途径：沿用或改进区域版本的传统扰动方法、动力降尺度和专门为区域集合预报设计新的扰动方法[5]。沿用区域版本的传统扰动方法需要面对的主要问题是如何准确描述中小尺度波动的不确定性。对于增长模繁殖法，Pena 等[16]指出，6 h 的时间间隔只能繁殖出天气尺度的扰动模态从而导致其在高分辨率模式下离散度不足。肖玉华等[17]利用η坐标有限区域数值预报模式AREM（Advanced Regional Eta-coordinate Model），设计了基于BGM 的动态初始扰动法，该方法在识别上升、下沉运动区的前提下，针对不同特性的区域叠加不同强度的扰动，结果表明动态扰动法增加了模式对垂直运动预报的发散程度。Chen 等[18]提出了局地增长模繁殖法（Local BGM，LBGM），通过邻域方法局部调整来获得小尺度扰动，在集合成员数不变的情况下，提高了对流尺度集合预报的离散度。最近，Li 等[19]在LBGM的基础上，在扰动培育阶段引入了高斯权重，结果表明基于高斯权重的LBGM 能有效改进原方法中的大尺度信息，对飑线降水结构的预报要优于等权重。产生区域集合预报初始扰动的另一种方法是动力降尺度，即将全球集合预报初值场直接降尺度至区域，此法简单易行。张涵斌等[20]比较了两种集合方案：直接动力降尺度和提取全球集合降尺度后的扰动，叠加至区域高分辨率分析场。试验结果表明，将全球集合降尺度后的扰动场与区域模式高分辨率分析场相结合效果更好。

区域版本的传统扰动方法和动力降尺度何者更优尚无定论[21-23]。基于前者缺乏大尺度不确定性信息而后者缺乏中小尺度不确定性信息的事实，许多学者尝试将二者结合，构建能够表征不同尺度不确定性的混合扰动方法。Wang 等[24]利用数字滤波和谱分析技术在BGM 生成的扰动中提取中小尺度扰动，与全球集合预报系统的降尺度扰动相结合，该方法所得集合的表现优于单一的BGM 和动力降尺度。庄潇然等[25]则通过Barnes空间滤波将来自ETKF 更新预报系统中的中小尺度扰动与动力降尺度扰动相结合，结果表明合适的滤波波段所构造的混合扰动可以改进降水概率预报。相关研究还证实，混合方法能够有效缓解区域初始扰动和来自全球集合的侧边界扰动在边界附近不匹配的问题[24-27]。除混合扰动法外，集合资料同化能提供和对流尺度模式相协调，且包含模式所能解析的所有尺度的初始扰动，但对流尺度集合资料同化仍在发展阶段且计算耗费颇高[9]。考虑到扰动的不同来源及其相互作用[12,15]，近年来许多学者提出和测试了多类型扰动组合的联合扰动法[28-29]，并应用于对流尺度，为集合扰动的构建提供了新思路。

长江中下游地区是我国重要的经济带之一，该地的暖季强降水受到不同尺度天气系统的共同影响，预报挑战性较大。最近研究表明，除活跃于梅雨锋附近的梅雨锋暴雨[30-31]外，长江中下游还存在远离锋面（100～300 km）、天气尺度斜压性强迫较弱的暖区暴雨[33-34]，这类过程局地性强、高度非线性，较难被模式捕捉，因而考虑不确定因素的集合预报成为重要选项[10,35-37]。许多集合试验的结果均表明中国的暖区暴雨具有较大的预报不确定性。Wu 等[35]通过优劣成员对比和扰动敏感性试验指出华南暖区暴雨的预报对夜间偏南风的加强和山地的冷却效应较为敏感，且此类过程可预报时效仅为6～12 h。Bao 等[36]通过一系列敏感性试验的结果认为华南暖区暴雨对流触发的模拟对由不同再分析资料所提供的初始场最为敏感，超过了微物理方案等其他因素的敏感程度。徐渊等[37]考虑了长江中下游暖区暴雨的可预报性问题，指出现阶段初始场和侧边界的不确定性仍给此类过程的预报带来较大的集合离差，但对流触发等阶段还受到混沌非线性特征的制约。谌芸等[38]对华北暖区暴雨预报失败案例的剖析也强调了微小扰动在对流的预报中可能引发的分岔，而使单一确定性预报失败。针对弱天气尺度强迫的局地性过程，扰动的增长性能及对流尺度集合预报效果是否敏感依赖于初始扰动的尺度特征，以及如何构建能在整个短时预报时效内（0～24 h）都能有效增长的初始扰动方案，尚不完全清楚。因而本文拟针对2018年5月4—5日一次典型的长江中下游暖区暴雨过程，通过动力降尺度（DOWN）、增长模繁殖法（BGM）、局地增长模繁殖法（LBGM）和混合扰动法（BLEND）四种具有不同尺度扰动信息的初始扰动方案分别进行对流尺度集合预报试验，探索初始扰动尺度特征在此次过程集合预报中所导致的差异性，以及不同尺度扰动分别在何种预报时段能够有效增长，产生较大的离散度或较优的预报效果。该研究的结果可为进一步改善对流尺度集合预报系统在长江中下游暖区暴雨过程中的预报效果提供借鉴。

2 研究方法概述

2.1 初始扰动方法

本文采用了四种初始扰动方案来构造有限区域集合预报的初始扰动。方案一为动力降尺度方法（Dynamic Downscaling，DOWN），该方法直接采用全球集合预报系统的分析扰动，插值叠加至模式的初始场上，提供区域集合预报的初始场[20]。本文在进行动力降尺度方法时使用了TIGGE计划中欧洲中期天气预报中心（ECMWF）的全球集合预报资料，它采用奇异向量法生成初始扰动，包含51 个集合成员，在全球中期集合预报效果的比对中表现良好[39]。DOWN 方法简单易行，但缺点是此方法产生的初始扰动只能代表天气尺度不确定性，而缺乏中小尺度不确定性信息[5,23]。

方案二为区域版本的增长模繁殖法（BGM），与应用于全球集合预报系统的BGM 方法类似，它包括植入随机种子、将误差场尺度化以更新扰动场和重复繁殖循环至饱和三个步骤[17,40]。其尺度化因子可表达为：

其中，ct(k)为第k个模式层上的尺度化因子，e0(k)是初始时刻第k层的均方根误差（RMSE），即初始模，e′t(k)是第k层的输出模。经过若干次繁殖循环，可消耗掉初始扰动中的衰减分量，而保留能够快速增长的分量。

Pena 等[16]指出传统的BGM 法只能繁殖出较大尺度的扰动模态从而导致其在高分辨率模式下离散度不足。针对此问题，方案三采用了Chen等[18]提出的局地增长模繁殖法（LBGM）。该方法在BGM 法的基础上，引入邻域半径r，通过邻域方法局部调整来获得小尺度扰动，其尺度化因子为[18, 41]：

其中输出模的计算方式为：

上式中，i、j、k分别为纬向、经向、垂直方向的格点序号，Xr(i,j,k)和Xcrl(i,j,k)分别表示叠加扰动的集合预报场和未叠加扰动的控制预报场。Chen 等[18]的敏感性研究指出取邻域半径r在7～13较为合适，但该结论从一次强飑线过程中得到，本文内区域分辨率与其一致，而研究对象为尺度更小且局地性更强的暖区暴雨，为着重体现LBGM方案中小尺度扰动的作用，取较小的邻域半径r= 8。

方案四在DOWN 和LBGM 的基础上，采用混合扰动的思想[24,42-43]，尝试构建能够表征不同尺度不确定性的混合扰动方法（BLEND）。该方案采用二维离散余弦变换和逆变换进行空间谱分析和构造滤波器[27,44]，它们定义为：

式中，

于是滤波场可表达为：

其中，φ[λ(m,n)]为滤波响应函数，Fc和F-1c分别为二维离散余弦变换和逆变换算子，此滤波方法可避免区域边界的不连续问题。将DOWN 经低通滤波后的初始场和LBGM 经高通滤波后的初始场等线性组合，得到BLEND的初始场：

该初始扰动场包含不同尺度不确定性信息。

以上四种初始扰动方案中，DOWN 直接来源于全球集合预报系统，因而仅含有大尺度扰动信息；BGM 和LBGM 是区域模式中的增长模繁殖法，包含中小尺度信息，而LBGM 是在BGM 的基础上，通过局部正交的思想改进得到的新方法，其中小尺度扰动具有更多的局地化特征；BLEND 则既包含LBGM 的中小尺度扰动分量，又包含DOWN 的大尺度扰动分量，具有各种尺度的扰动信息，从尺度特征来看最全面。

2.2 集合预报检验方法

采用区域平均的离散度（Spread）、集合平均预报场的均方根误差（RMSE）以及二者的比值q对降水场和要素场的集合预报效果进行定量化检验，其表达式为：

其中，Nx、Ny为纬向、经向的格点数，Nm为集合成员数为集合平均预报场为真值场。在本文中，降水场采用中国自动站与CMORPH 降水产品融合的逐时降水量网格数据集1.0 版（分辨率0.1 °×0.1 °）作为观测，该数据集能较合理地反映降水的空间结构[45]，后文将其双线性插值到模式空间作为参考真值来评估降水场集合预报的效果。对要素场集合预报效果的评估则选用ECMWF 的ERA5 再分析资料（分辨率0.25 °×0.25 °）作为参考真值。

在降水场集合预报的基础上，进一步通过邻域集合概率法产生降水概率预报[46]，邻域集合概率（Neighborhood Ensemble Probability，NEP）的表达式为：

其中，BP 为给定阈值的情况下，二进制化后的降水场，邻域半径r仍取8。对降水概率预报的检验则采用布莱尔评分（Brier Score，BS）和分数技巧评分[47]（Fraction Skill Score，FSS），即，

其中，P为概率预报场，O为二进制化处理后的降水观测场。对于一个理想的概率预报，BS 等于0而FSS 等于1。对于降水概率预报的检验，除定量化的评分外，还绘制了可信度（reliability）图和相对 作用 特征（Relative Operating Characteristic，ROC）曲线[48]，这些图表可以从可信度和可辨识度等方面直观呈现概率预报的质量。

检验分级直方图也叫Talagrand 图，它用以展示观测与相互独立的集合成员的预报之间的关系，反映出集合（概率）预报的偏差[49]。它首先对检验区域每个格点上的Nm个集合成员预报进行排序，划分出Nm+1 个区间，然后计算观测值落在某个区间的频率。频率的分布型态可以反映集合预报的系统误差，理想状态的集合预报呈均匀分级的分布。

3 天气过程概况和集合预报试验

3.1 天气过程概况

本文所选个例为2018年5月4—5日长江中下游地区的一次暴雨过程。分析ERA5 再分析资料所给出的天气尺度环境场（图1）可知，本次过程远离500 hPa高空槽且地面无大尺度低压系统，同时该过程发生于天气尺度锋面（以850 hPa相当位温等值线密集区表征）西南侧的低空急流区，距离锋面超过200 km，因而天气尺度斜压性强迫较弱，是一次典型的长江中下游暖区暴雨[33-34]。

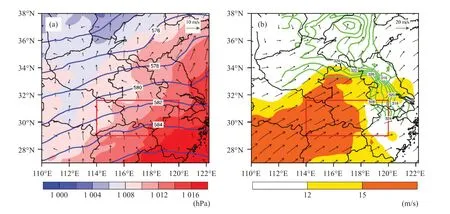
图1 2018年5月4日21:00 500 hPa位势高度（蓝色等值线，单位：dagpm）、海平面气压（填色，单位：hPa）和10 m风场（矢量，单位：m/s）（a）、850 hPa相当位温（绿色等值线，单位：K）、风场（矢量，单位：m/s）和风速（填色，单位：m/s）（b）的分布图红框为区域Ⅰ，此处表征过程发生位置。

进一步使用中国自动站与CMORPH 降水产品融合的逐时降水量网格数据集1.0 版作为观测来分析实况降水。该过程的最大瞬时雨强达20 mm/h，根据降水场的落区，可将本次过程划分为两个阶段（图2）。第一阶段为5月4日12:00（世界时，下同）—23:00，降水区主要位于湖北、江西、安徽三省（图2a～2b 红框）；第二阶段为5 月5 日00:00—06:00，降水区东移至安徽浙江交界及浙江沿海一带（图2c～2d 蓝框）。将两个阶段的降水区分别记为区域Ⅰ和Ⅱ，便于后文对预报效果进行定量检验。

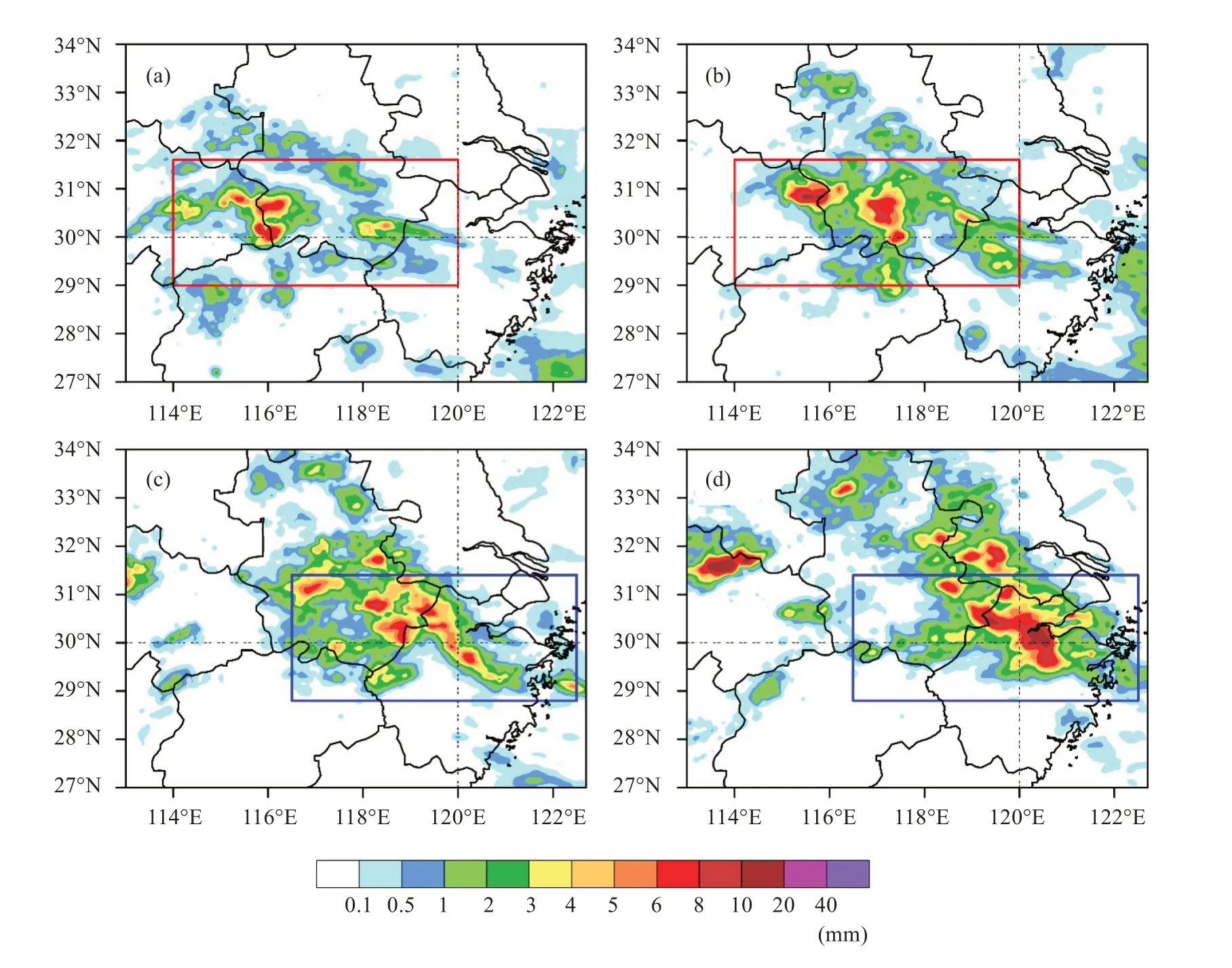
图2 2018年5月4日20:00（a）、22:00（b）、5月5日00:00（c）、02:00（d）逐小时降水量（单位：mm）（a、b）红框为区域Ⅰ，（c、d）蓝框为区域Ⅱ。

3.2 模式配置和集合预报试验

模拟采用WRF-ARW 模式3.7.1 版本，使用了两层单向嵌套网格（图3a），外区域分辨率为12 km，格点数为179×232，覆盖中国东部；内区域分辨率为3 km，格点数为277×361，覆盖长江中下游地区的大部分。选用Thompson 微物理方案、RRTM 长波辐射方案、Dudhia 短波辐射方案、YSU边界层方案和Kain-Fritsch 积云对流方案（仅外区域）等物理过程参数化方案，这些方案在长江中下游地区暴雨过程的模拟中表现良好。控制预报（CTRL）未添加任何扰动，使用ERA5 0.25 °×0.25 °的再分析资料作为模式积分的初始场，积分起始时间为2018 年5 月4 日12:00，积分18 h 至5日06:00。

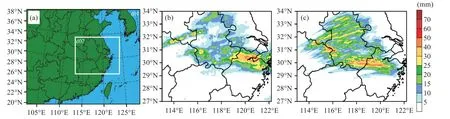
图3 WRF模式模拟区域（a）以及实况（b）和CTRL（c）2018年5月4日18:00—5日06:00 12 h累积降水量（单位：mm）

图3b、3c 给出了CTRL 和实况的12 h 累积降水（5 月4 日18:00—5 日06:00）分布，对比可见CTRL较好地模拟了暖区降水的两个中心，分别位于安徽西南山区和浙江北部，只是位置和强度上略有偏差。因此，在CTRL 初始场的基础上叠加扰动来进行集合预报试验，不至引起较大的系统性偏差。

分别采用四种方案来进行初始扰动集合预报试验。方案一采用2.1 节所述的动力降尺度方案，使用的全球扰动来自TIGGE计划中ECMWF全球集合预报系统中的分析扰动（随机挑选12 个成员），经双线性插值降尺度后叠加至CTRL 所采用的内、外区域的初始场上，该方案记为DOWN。方案二为区域版本的BGM 方法，成员数也为12，繁殖时间为3 d，周期为6 h，内外区域均参与了繁殖循环。方案三采用LBGM 方法，邻域半径取8，其余与方案二相同。方案四采用混合扰动法，将方案一DOWN 方法得到的初始扰动通过低通滤波器、方案三LBGM 方法得到的初始扰动通过高通滤波器，进而将二者等权线性组合。其中，滤波的节点W1=256 km 和W2=512 km 经过敏感性测试选取，滤波响应函数如图4 所示，图中W1～W2 为过渡波段，在该波段同时包含DOWN 和LBGM 的扰动分量，设置过渡波段的目的是保证滤波响应函数的连续性，将该试验记作BLEND。四种方案的扰动变量均为纬向风u、经向风v、温度T和水汽混合比Qv，且均采用由ECMWF 全球集合预报系统的分析扰动降尺度所提供的侧边界扰动，用以研究单一初值扰动方案的影响，四种方案的其余详细描述见2.1节。表1对四种初始扰动方案进行了汇总。

表1 四种初始扰动方案

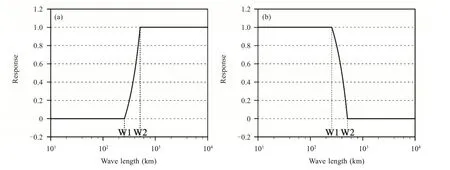
图4 BLEND方案中，低通滤波的响应函数，作用于DOWN的初始场（a），和高通滤波的响应函数，作用于LBGM的初始场（b）

图5 给出了四种方案内区域集合平均的850 hPa 初始扰动功率谱图，其他层次与之类似。可以看到，对于所有变量，初始扰动的功率谱函数均随尺度的增加而增大。其中，BGM（蓝色点虚线）和LBGM（紫色点虚线）在中小尺度上的功率谱均明显高于DOWN（黑色实线），说明区域模式的增长模繁殖法能够繁殖出中小尺度扰动，DOWN 则几乎不包含中小尺度扰动；而DOWN 在较大尺度上的功率谱则高于BGM 和LBGM，体现出DOWN 具有更多的大尺度扰动信息。对比BGM 和LBGM 发现，LBGM 在中小尺度上的功率谱高于BGM，表示LBGM 包含更多的中小尺度不确定性信息，这表明LBGM 在一定程度上达到了对BGM 的改进目的，获得了更丰富的中小尺度扰动。而BLEND（红色虚线）则在中小尺度接近LBGM，在较大尺度接近DOWN，因而几乎在所有尺度都具有较高的功率谱，表明整个混合过程是合理有效的。

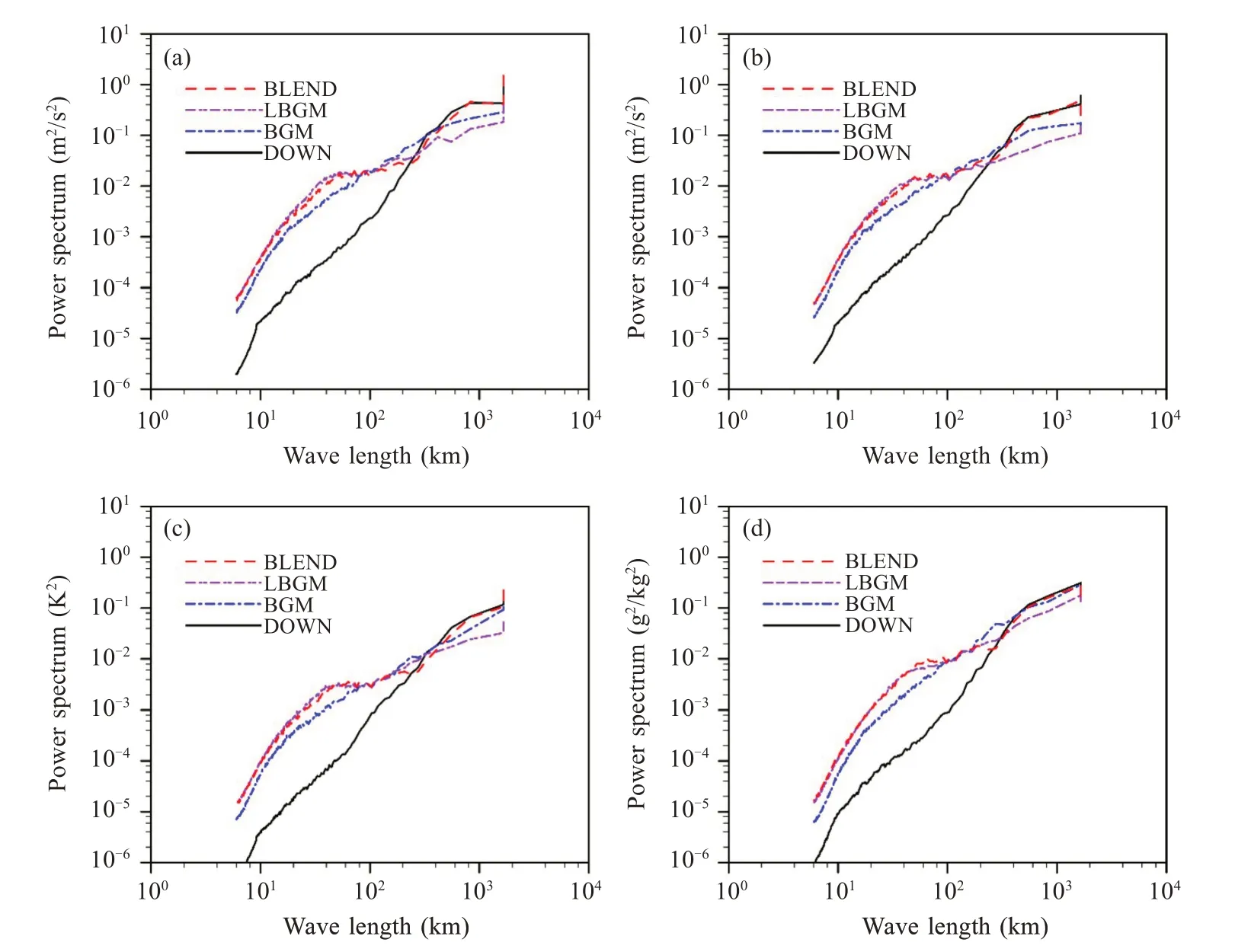
图5 内区域集合平均的850 hPa纬向风（a）、经向风（b）、温度（c）、水汽混合比（d）初始扰动功率谱黑色实线为DOWN，蓝色虚线为BGM，紫色虚线为LBGM，红色虚线为BLEND。

4 集合预报检验

4.1 降水场检验

根据暖区降水的时间和落区，选取了合适的检验区域，其中，2018 年5 月4 日12:00—23:00 采用区域Ⅰ（图2a～2b 红框），5 月5 日00:00—06:00 采用区域Ⅱ（图2c～2d蓝框）。图6给出了检验区域逐小时降水量的时间序列。DOWN在积分初始阶段（0～6 h）离散度最小；而LBGM 的离散度高于BGM，显示出局地正交的策略在对流尺度集合预报中的优越性；BLEND 在积分初始阶段也取得了类似LBGM 的集合成员分布，尽管在某些时刻离散度略小于LBGM，但整体而言依然保留了LBGM 的特点，相对DOWN 而言则改进明显。但是在积分12 h 后，BGM 和LBGM 的降水序列，其离散度都明显小于DOWN；而BLEND 则仍然保留了DOWN 的特性，相比BGM 和LBGM，具有明显的离散度优势。

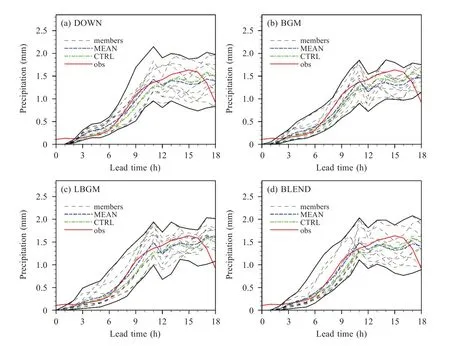
图6 检验区域DOWN（a）、BGM（b）、LBGM（c）和BLEND（d）逐小时降水量时间序列红色实线为观测，绿色虚线为CTRL，灰色虚线为集合成员（members），蓝色虚线为集合平均（MEAN），黑色粗实线为集合成员的包络线。

上述特点在图7a 离散度的时间序列中，也得到与图6 相一致的定量反映。同时，图7b 显示，DOWN 在积分3～6 h 时的均方根误差要略大于其他方案，而在积分12 h 以后，DOWN 和BLEND 的均方根误差则要显著小于BGM 和LBGM。最终在离散度与均方根误差比值的时间序列（图7c）中，则反映为积分0～9 h LBGM明显大于BGM，而BGM 明显大于DOWN；BLEND 则和LBGM 很接近，但在积分3～9 h 仍略低于LBGM，这可能由于滤波波段的选取基于功率谱分析的结果由敏感性测试得到，后期将致力于发展更精确的定量方法来确定滤波波段和响应函数，或可做进一步的改进。而在 积 分12～18 h 则相 反，DOWN 相 比于BGM 和LBGM 具有更高的比值，BLEND 则接近于DOWN，仍然维持在较高水平。这表明在降水场上，对于积分初始阶段（0～6 h），LBGM 对BGM有较好的改进作用，而这一阶段DOWN 表现较差；但是随着积分时间的延长，到了积分12 h 后，DOWN 的降水场集合预报效果则明显好于BGM和LBGM；而BLEND 则几乎在整个预报时段都具有较高的离散度和较低的均方根误差，因而结合了LBGM 在积分初始阶段和DOWN 在积分12 h后的优点，综合来看具有最好的集合预报效果。

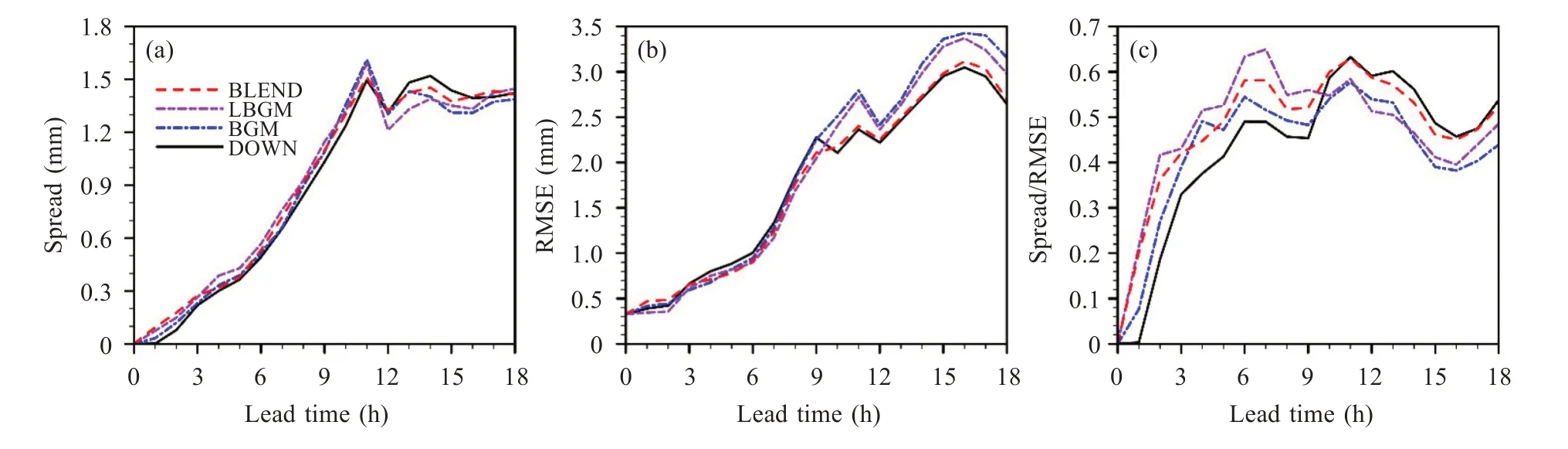
图7 检验区域逐小时降水量Spread（单位：mm）（a）、RMSE（单位：mm）（b）和Spread/RMSE（c）随时间的演变

以上对降水场集合预报结果的分析发现，BGM 和LBGM 的离散度在积分初始阶段增长较快，二者之中LBGM 还要略占优势；而DOWN 在积分12 h后对离散度的维持要显著优于增长模繁殖法，且这一阶段该方案的RMSE 也更小。BLEND 则兼具LBGM 和DOWN 的优势，其离散度既能在积分初始阶段获得较快增长，又能在积分一段时间后得以维持。

4.2 降水概率预报

图8给出了在给定阈值的情况下四种方案6 h累积降水量的概率预报，产生概率预报的方法为2.2 节中所述的邻域集合概率法。其中，图8a1～8a4为5 月4 日12:00—18:00，采用的阈值为3 mm；图8b1～8b4为5 月5 日00:00—06:00，采 用 的阈 值为13 mm。黑色粗实线则绘制出观测的6 h 累积降水量在阈值处的等值线，结合概率预报大值区的模态可见，在积分的前6 h（图8a1～8a4），DOWN 的概率预报大值区相对于观测的降水量等值线轮廓明显偏东，而BGM 和LBGM 中二者的位置更为匹配，其中LBGM 对应得更好。同时，BLEND 中概率预报大值区与观测的降水量等值线轮廓也具有相对较好的对应关系。从检验区域的概率预报评分上看，DOWN 的BS（FSS）最大（小），LBGM 的BS（FSS）最小（大），而BLEND 的BS 和FSS 则与LBGM 较为接近，表明BLEND 主要继承了LBGM的预报特点，在积分6 h 效果较优。从可信度图（图9a1～9a4）中则可以看到，在积分的前6 h，相较于DOWN 和BGM 的过度预报偏差，LBGM 有效减小了对小概率事件的过报但对大概率事件也有一定低估，尽管如此仍可认为分辨率好于DOWN和BGM。而BLEND 也在一定程度上减小了对小概率事件的过报，尽管改进幅度略弱于LBGM，同时其对大概率事件也并未过分低估。此外，从ROC 曲线（图9c1～9c4）上，LBGM 相较于DOWN 和BGM，提升了小概率事件的辨识度，因而曲线下方面积（用梯形法求得，表征预报技巧）最大，BLEND 总体上有效继承了LBGM 在积分初始阶段的较优表现。

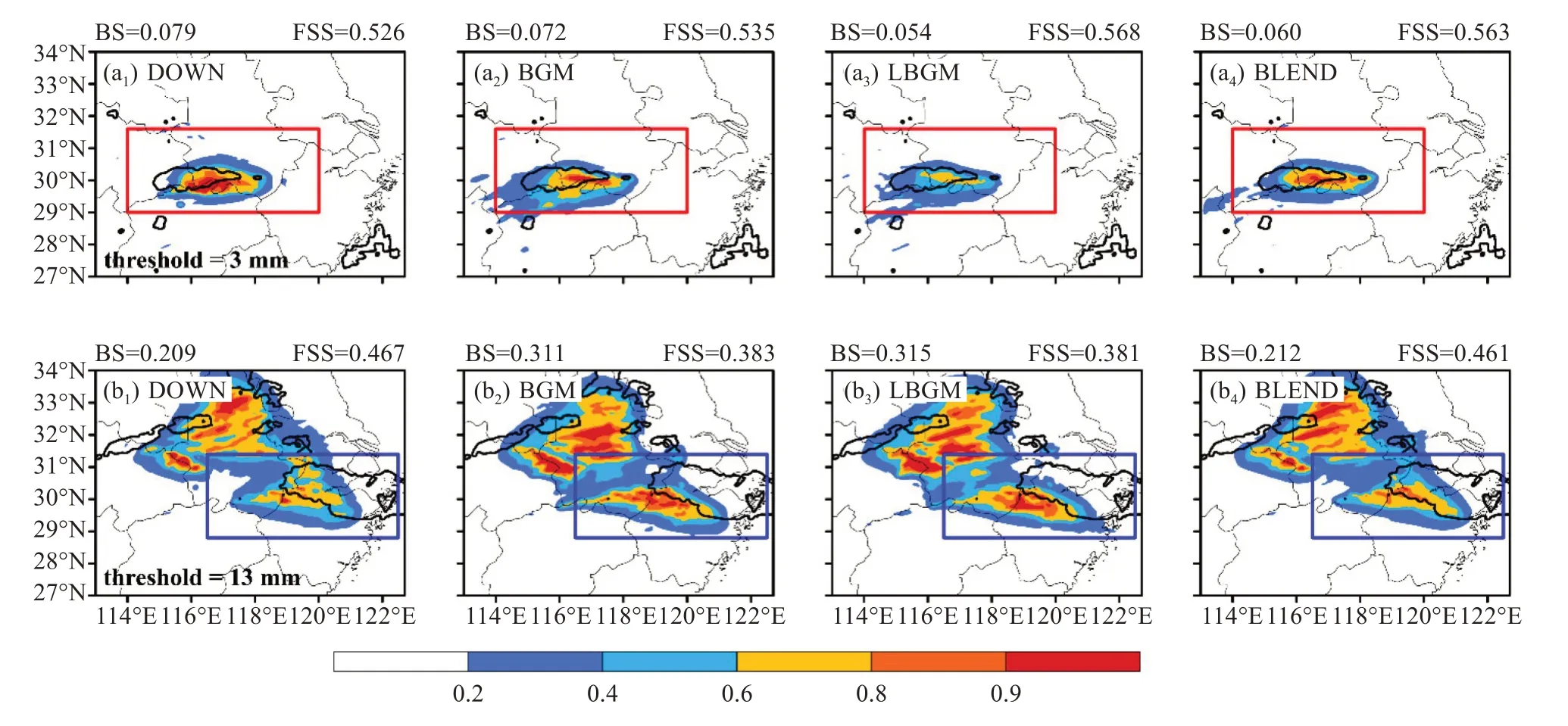
图8 2018年5月4日12:00—18:00 DOWN（a1）、BGM（a2）、LBGM（a3）、BLEND（a4）6 h累积降水量的概率预报和2018年5月5日00:00—06:00 DOWN（b1）、BGM（b2）、LBGM（b3）、BLEND（b4）6 h累积降水量的概率预报黑色粗等值线为观测的6 h累积降水量在阈值处的等值线，BS、FSS和阈值在图上标出，a1～a4红框和b1～b4蓝框为检验区域Ⅰ和Ⅱ。

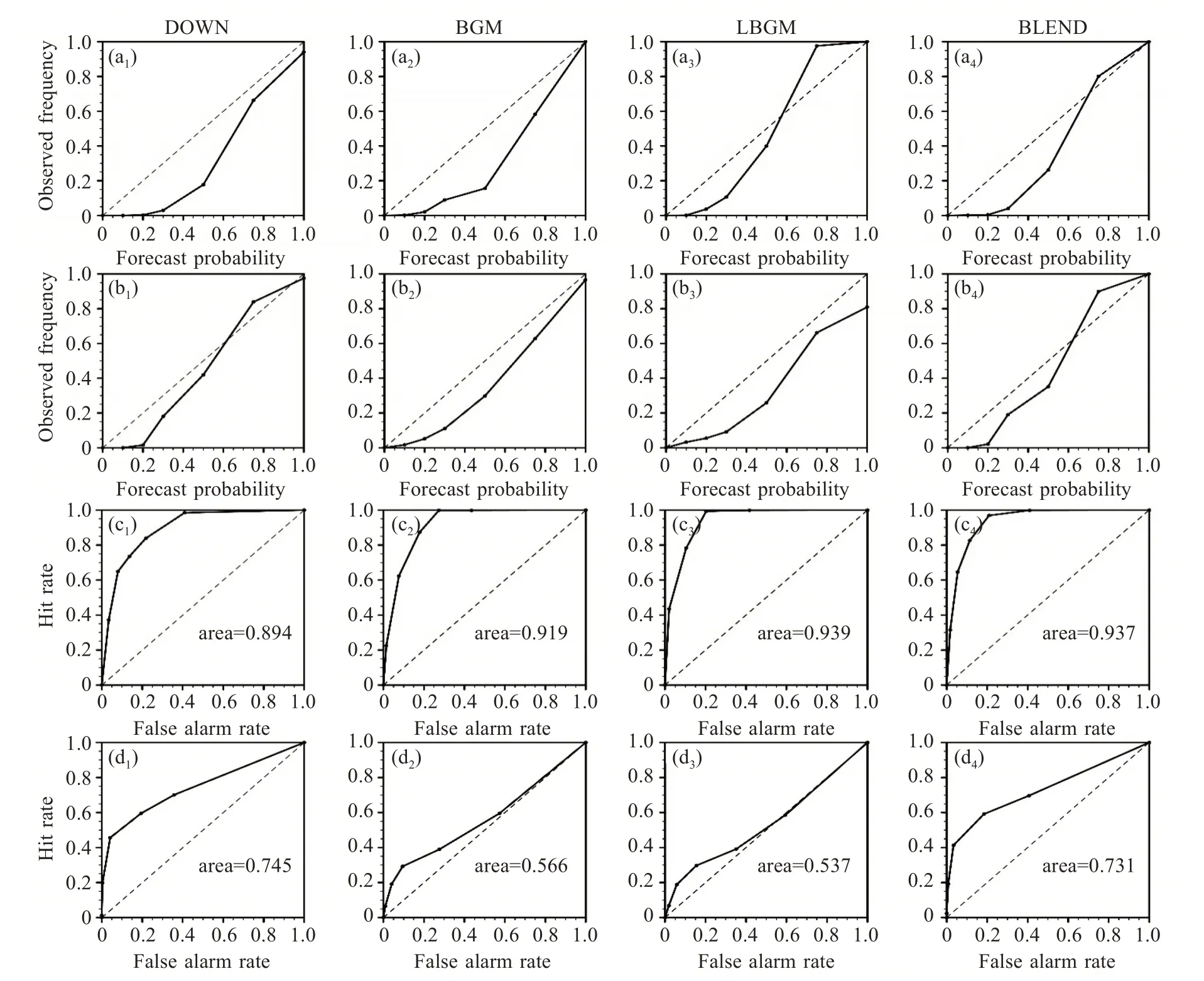
图9 2018年5月4日12:00—18:00 6 h累积降水量概率预报的可信度图（a1～a4）、相对作用特征曲线（b1～b4）和2018年5月5日00:00—06:00 6 h累积降水量概率预报的可信度图（c1～c4）、相对作用特征曲线（d1～d4）第1～4列分别为DOWN、BGM、LBGM和BLEND。

对于积分12 h 后（图8b1～8b4），针对蓝框中的暖区降水，BGM 和LBGM 的降水概率预报大值区显著偏西，而DOWN 则更为匹配，在这一阶段，BLEND的降水概率模态更接近于DOWN，也表现较优，说明在预报一段时间后大尺度扰动逐渐起到决定性的作用。从BS 和FSS 上也可以看出，DOWN和BLEND的BS（FSS）显著低（高）于BGM和LBGM，进一步体现出DOWN 在积分较长时效的预报优势以及BLEND 在此类过程对流尺度集合预报中的可行性。同时该阶段选取的阈值13 mm 已达到业务上大雨标准，表明BLEND 在强降水过程中效果良好。从可信度图（图9b1～9b4）可见，BGM 和LBGM 对大概率事件（概率大于0.6）有较明显的高估，DOWN 对大概率事件的表现优于BGM 和LBGM，BLEND 在这一阶段与DOWN类似，均避免了BGM 和LBGM 的无条件偏差。从ROC 曲线上看（图9d1～9d4），DOWN 对大概率事件的辨识度要显著好于BGM 和LBGM，因而曲线下方的面积显著大于BGM 和LBGM，而BLEND 则有效继承了DOWN 在这一阶段的优势，也能较好改善对大概率事件的辨识能力。

本节在通过邻域集合概率法生成降水概率预报的基础上，从其模态、评分（准确性）和可靠性及可分辨性等方面对四种初始扰动方案的结果进行了对比分析。在模式积分初期的6 h 内，LBGM的降水概率预报大值区比DOWN 更符合实际降水大值的分布，概率预报的BS 和FSS 也更优，且较好改进了BGM 和DOWN 对小概率事件的过报，对小概率事件辨识度更高；而在积分12 h 以后，则是DOWN 效果更好，且避免了BGM 和LBGM 中的无条件偏差，对大概率事件具有很好的辨识能力。BLEND 在积分初期和LBGM 较为一致，而在积分12 h 后则更接近于DOWN，均具备较优的结果，进一步体现了其在降水概率预报中的优势。

4.3 基本物理量场检验

由于降水量是模式预报的诊断量，而非直接预报变量，因而仅从降水场的角度来比较各种初始扰动方案的优劣仍然不够全面。因此，本节将从大气基本物理量场的角度，再次检验四种初始扰动方案的集合预报效果，以达到补充说明的目的。

图10 为近地面要素10 m 纬向风和经向风、2 m 温度和水汽混合比的离散度时间序列。由于近地面变量未添加初始扰动，因而离散度均从零开始增长。对于10 m 纬向风，BLEND 和LBGM在积分4 h 前离散度明显高于BGM，同时DOWN在这一阶段离散度则为四种方案中最低。此后在积分5—10 h 的时间内，四种方案的离散度相仿。积分10 h 后BLEND 和DOWN 的离散度增长则快于BGM 和LBGM。10 m 经向风的特点基本与纬向风类似，但在积分0—9 h 的时间范围内，LBGM的离散度均高于BGM，BLEND 同样在该时段接近LBGM，而在积分12 h 后接近DOWN，达到了混合扰动的预期效果。2 m 温度和湿度场上的特征也与风场很相似，但是对于湿度场而言，BGM和LBGM 在积分0—6 h 内离散度相对于DOWN的增加幅度要明显低于温度场，表明增长模繁殖法在湿度场离散度的增长方面仍存在一定缺陷。

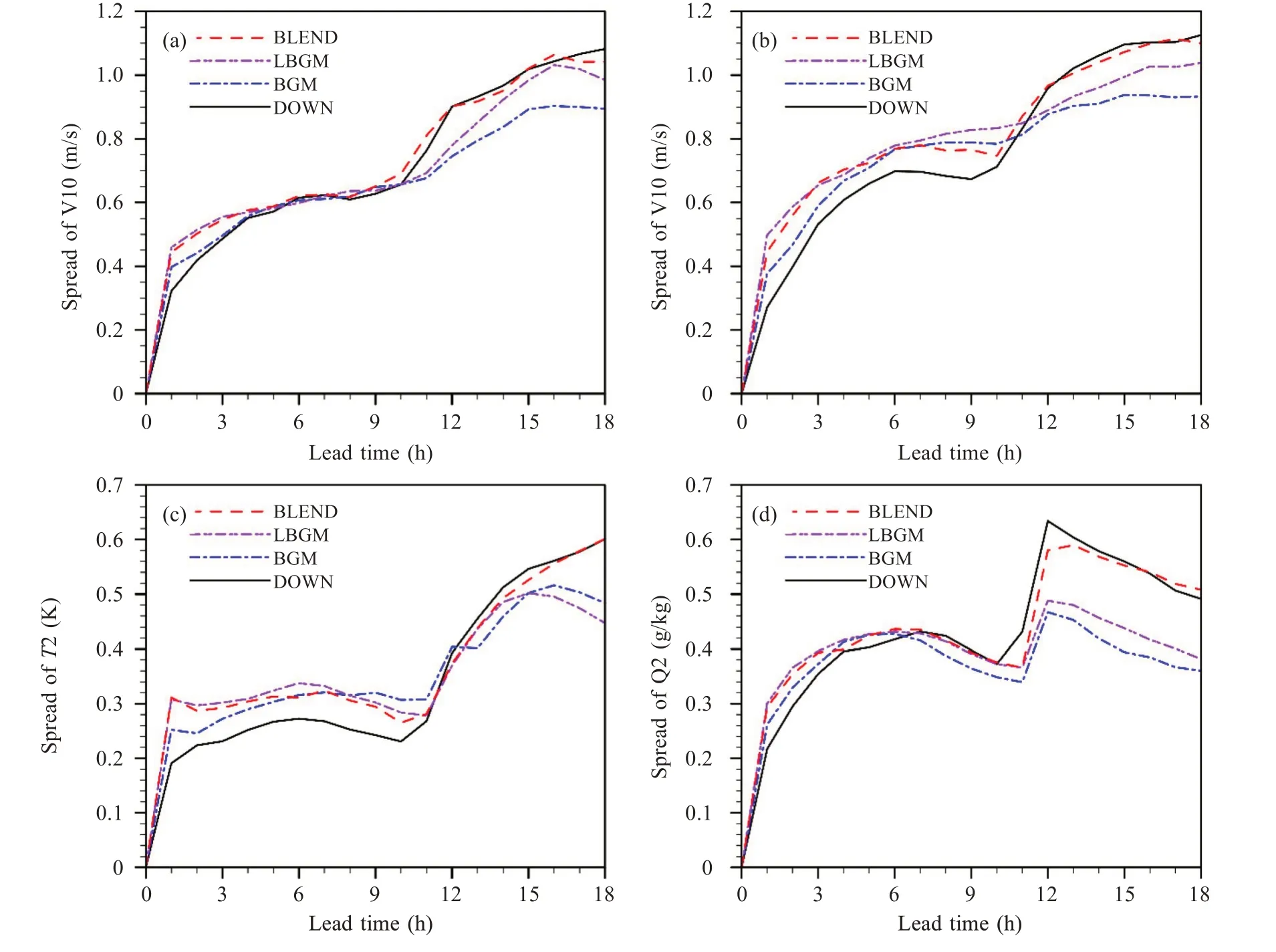
图10 10 m风场（a、b）、2 m温度（c）和2 m水汽混合比（d）离散度随时间的演变

图11 给出了850 hPa 上积分6 h（a～b）和积分18 h（c～d）水平动能Kh和温湿能hm的Talagrand 分布，其中水平动能和温湿能分别用以代表动力场和热力场，它们的表达式为：

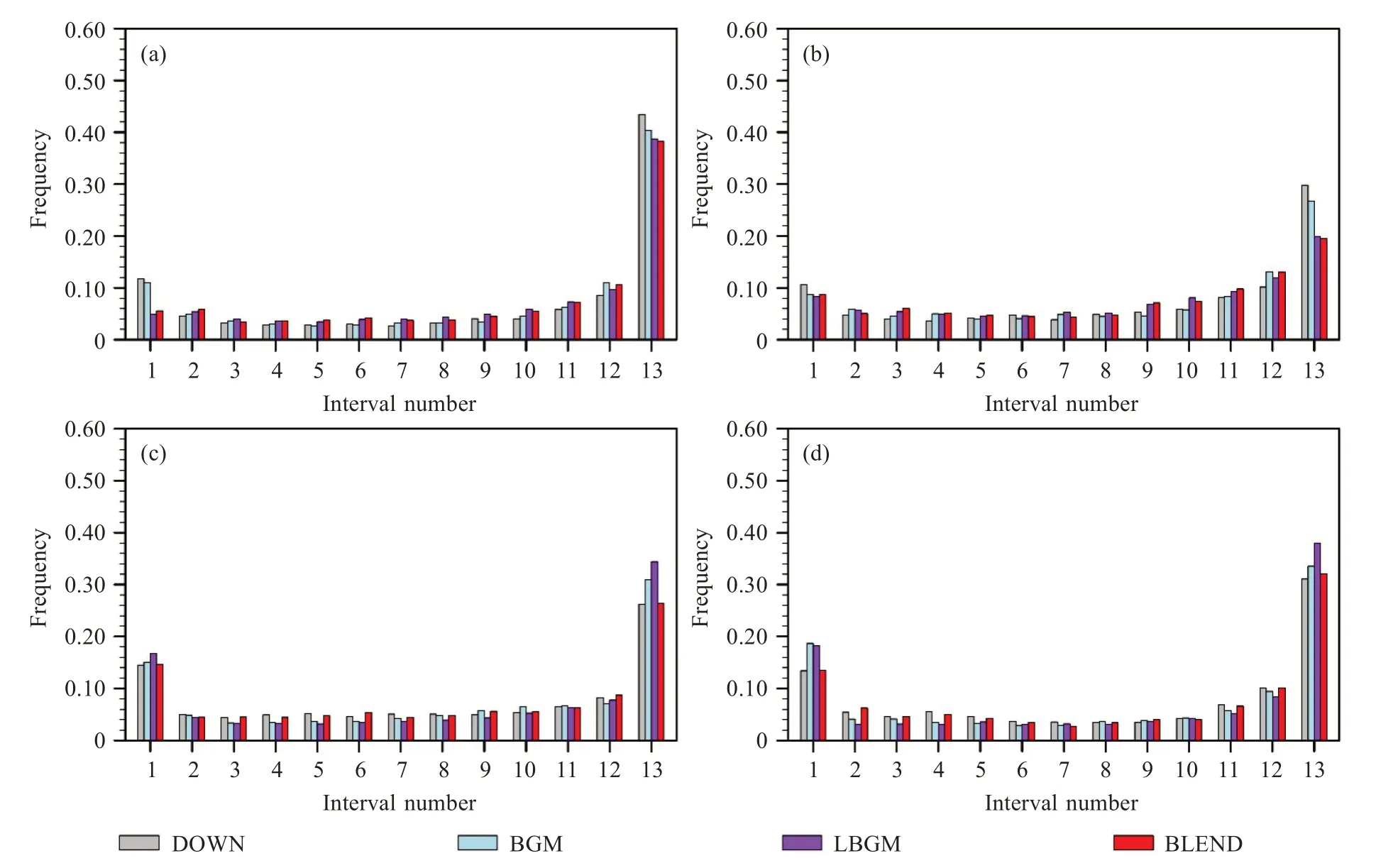
图11 850 hPa上积分6 h水平动能（a）、温湿能（b）和积分18 h水平动能（c）、温湿能（d）的Talagrand分布

式中，Cp为比定压热容，L为潜热通量系数，u、v、T、q分别为纬向风、经向风、温度和比湿。从图中可见，各方案的频率分布大致都呈“U”型，表明集合成员都较难涵盖观测值，这充分显示了对流尺度集合预报所常见的“离散度不足”问题[50-51]。

具体来分析，对于积分6 h 时（5 月4 日18:00）的水平动能而言（图11a），DOWN方案频率分布的“U”型型态最明显，意味着有较多观测落在集合成员预报的等级边缘或之外，而BGM 和LBGM 相对于DOWN 则有一定优势，尤其在两侧第1 和第13个区间上，频率都有一定程度的减小，表明相比于DOWN，其观测更集中于中间一些，二者之中LBGM 的 优 势 更 大。BLEND 则 与LBGM 高 度 相似，也在该时刻较优。对于积分6 h 的温湿能（图11b）而言，其特征与同时刻的水平动能类似，只不过LBGM 相对于DOWN 和BGM 的改进幅度要更大一些，主要体现在对负偏差的消除上（区间13）。而对于积分18 h 时（5 月5 日06:00，图11c～11d），情况则相反。无论是从水平动能还是温湿能上看，DOWN 的“U”型型态相比BGM 和LBGM 都有所减缓，也即DOWN 更趋向于均匀分布一些，表明这一时刻DOWN 的集合预报效果更优，而BLEND 在此时则接近于DOWN。BLEND 方案在选取的两个代表时刻，都具有相对更接近均匀分布的Talagrand 分布型，因而在四种方案中总体表现最好，这和前文描述的近地面变量的离散度特征具有一定的相似性。

近地面和等压面上大气基本物理量场的检验结果和降水场较为匹配，这些结果共同表明，在积分初始阶段，具有中小尺度扰动信息的BGM 和LBGM，其离散度、概率预报模态及评分和Talagrand 分布等指标相比于DOWN 都具有一定优势，说明在该阶段增长模繁殖法所包含的中小尺度扰动更能够得到有效增长，同时LBGM 的效果要总体优于BGM，则显示出该方案更适合于对流尺度的模拟；而在积分较长时效后（如12 h）则相反，包含更多大尺度扰动信息的DOWN 要明显优于BGM 和LBGM，体现出这一阶段大尺度扰动信息的平稳与控制作用；具有不同尺度混合扰动信息的BLEND 方案，则在积分初始阶段（0—6 h）和LBGM 相似，在积分较长时效后（12 h 后）和DOWN 相似，因而几乎在所有预报时段均能够取得相对较优的效果，在四种方案里优势最显著。Zhang 等[52]所提出的湿对流下误差增长的三阶段概念模型认为，中小尺度扰动在高分辨率模式的积分初期能够以较快速度增长并逐渐开始升尺度转换，最终在积分一段时间后成为大尺度扰动的一部分；而准确的大尺度扰动则能在预报后期有效增长，并逐渐起到决定性作用，上述结果与之相吻合。以上结果也进一步证实了此类暖区暴雨过程的对流尺度集合预报效果对初始扰动尺度特征的敏感性，在此基础上设计的混合扰动方法在业务上具有应用和推广价值。

5 结果与讨论

本文针对2018年5月4—5日一次弱天气强迫背景下的长江中下游暖区暴雨典型个例，采用四种包含不同尺度信息的初始扰动方法进行了对流尺度集合预报试验，包括动力降尺度法（DOWN）、增长模繁殖法（BGM）、局地增长模繁殖法（LBGM）和混合扰动法（BLEND）。在选取暖区降水为检验区域的基础上，通过多种定量方法对降水场和大气基本物理量场进行了集合预报效果的检验与分析，得到以下结论。

（1）此类过程的对流尺度集合预报效果对初始扰动的尺度特征较为敏感。在积分初始阶段（如0—6 h），具有中小尺度扰动信息的BGM 和LBGM，效果均优于DOWN。说明准确的中小尺度扰动可以在这一阶段有效增长，从而增强对预报不确定性的覆盖能力。

（2）LBGM 是在BGM 的基础上，经局地正交改进处理后得到的新方案，包含更丰富的中小尺度扰动信息。在积分初始阶段，LBGM 的集合预报效果总体上优于BGM，且由LBGM 产生的降水概率预报对于小概率事件的辨识度更高，说明在区域高分辨率集合预报中，LBGM 充分考虑了中小尺度天气系统的局地性，确实能够有效弥补BGM的不足。

（3）DOWN 直接从全球集合预报系统中获取集合扰动，在积分较长时效后（如12 h），具有更多大尺度扰动信息的DOWN，集合预报效果普遍优于BGM 和LBGM，且由DOWN 产生的降水概率预报对于大概率事件有良好的辨识能力，说明经过初始扰动快速增长一段时间后，大尺度扰动开始逐渐起到主要作用。

（4）BLEND 组合了LBGM 的中小尺度扰动分量和DOWN 的大尺度扰动分量，总体而言具有不同尺度混合扰动信息的BLEND，几乎在整个预报时效（0—18 h）内，都具有较优的集合（概率）预报结果，说明混合扰动能继承LBGM 在积分初始阶段和DOWN 在积分较长时效后的优势，在此类过程的对流尺度集合预报中具备优越性。

因而在实际业务中，如果追求短时集合预报效果，那么需要着重考虑初始扰动所包含的中小尺度特征是否显著，此时可以考虑采用具有中小尺度特征的初始扰动方法；而如果追求更长时效的预报效果，则需着重考虑大尺度扰动，此时动力降尺度方法是较优的选择。Zhang 等[15]针对华南暖区暴雨的研究也指出不同尺度特征的扰动具有不同的增长行为，其中，中-β尺度扰动增长更快且更早饱和，这与本文的结果具有相似性。此外，对于混合扰动法，Wu 等[35]对华南暖区暴雨的集合模拟，也在整个短时预报时效内均产生了较高的离散度，优劣成员间的差异明显。由此可见，针对此类局地性较强的暖区暴雨，考虑发展包含丰富中小尺度扰动信息的初始扰动新方法，并通过滤波技术与动力降尺度法相混合，得到包含不同尺度扰动信息的混合初始扰动，也是一种较为科学有效的对流尺度初始扰动构造思路。尽管如此，针对暖区暴雨关于初始扰动敏感性的研究仍不多见，不同初始扰动方法下对流尺度集合预报结果的个例依赖性也需要更多相关研究继续考证。