基于 PID/LQR 凿岩机器人机械臂控制算法

王 辉，盛 荣，郭剑东

1南京航空航天大学自动化学院 江苏南京 210016

2徐州威卡电子控制技术有限公司 江苏徐州 221122

3南京航空航天大学中小型无人机先进技术工信部重点实验室 江苏南京 210016

凿 岩机器人控制的关键点是钻臂移动及定位控制，其臂架多数为采用三角结构且具有冗余自由度的机械臂，是一种多输入多输出、交叉耦合的非线性系统控制。在小负载机器人领域，Jiang 等人[1]实时测量跟踪机械臂的运动，利用在线测量数据进行不断迭代补偿从而提高精度。陈绵鹏等人[2]利用Levenberg-Marquardt 算法辨识出误差模型中的误差参数并进行补偿，最终提高机械臂末端定位精度。Zhang 等人[3]利用曲线拟合方法识别机械臂末端运动轨迹特征，实现机械臂 D-H 模型中的参数校准。周宏兵[4]着眼于整个钻臂的运动分析，建立了钻臂运动学方程，但是没有对三角钻臂进行运动分析。周永行等人[5]研究了 2 个驱动变量 (驱动液压缸) 和 2 个目标参数 (机械臂的空间位置) 之间的耦合关系，借助空间几何的方法得到了近似的线性关系，实现了钻臂的运动控制，但是推导中对三角支撑的驱动机构进行了简化，会带来控制误差。凿岩机器人通常在隧道中进行工作，小负载机器人领域中的方法难以满足其恶劣工况。凿岩机器人机械臂属于复杂的非线性系统，机械臂受重力影响柔性变形较大，所以曲线拟合和空间插值方法在凿岩机器人误差补偿应用中具有一定的局限性。

笔者首先构建单三角钻臂运动学模型，对钻臂支臂缸进行运动学解算，从理论上对三角钻臂进行运动学解耦，得出驱动液压缸变量和机械臂空间位置之间的关系，并使用 PID 算法[6]对机械臂进行控制，而后对凿岩机械臂进行动力学建模，提出一种线性二次型调节器 LQR (Linear Quadratic Regulator)[7-8]，并对控制器进行仿真和试验比对控制效果，验证了控制器的有效性。

1 凿岩机器人机械臂简介

1.1 单三角结构钻臂

单三角凿岩机器人的钻臂结构如图1 所示，阿特拉斯 Boomer-XE3C 以及新一代的凿岩机器人均使用该类型臂架结构。

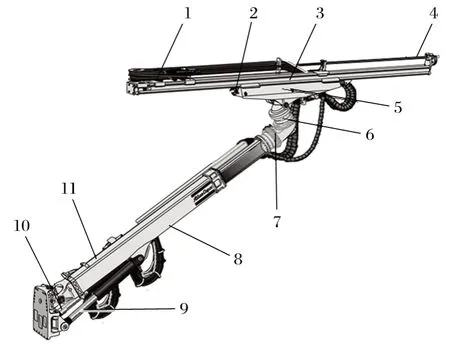
图1 单三角结构钻臂Fig.1 Single triangular structure drilling arm

钻臂左支臂缸 Cb1 和钻臂右支臂缸 Cb2 形成三角臂，控制大臂的摆动和俯仰，伸缩液压缸 Cz 用于实现钻臂的长度变化，推进器翻转液压缸 Cr 用于实现推进器的轴向旋转，推进器补偿液压缸 Ce 用于补偿推进器的前后位移，推进器俯仰液压缸 Cl 实现推进器的俯仰变化，推进器摆动液压缸 Cg 实现推进器的左右摆动。钻臂左右 2 个支臂缸配合动作实现大臂的俯仰和摆动，为达到精准定位目的，需要精准控制2 个支臂缸的伸缩。控制 2 个支臂缸的难度要高于其他液压缸的控制器，因此有必要对三角定位机构的控制进行研究。

1.2 钻臂支臂缸运动学解算

左右支臂缸同时控制大臂摆动和俯仰，控制大臂摆动角度同时会影响到大臂俯仰角度，因此这是一个典型的 MIMO 控制系统，必须对支臂缸进行运动学分析，推导出从大臂空间角度到驱动缸长度的运动学公式，为实现精确运动控制奠定基础。

如图2 所示，以左右钻臂液压缸轴套与车体的连接点B、C的中点O为坐标系原点，钻臂与车体的连接轴A为坐标系的z轴，O点沿大臂方向水平向前为x轴，y轴由右手定则确定，R点为大臂后铰点与轴套的铰接点，G点为右液压缸后铰点与轴套的铰接点，E点为左液压缸后铰点与轴套的铰接点，N、M点为大臂和液压缸的铰接点，△JMN为垂直于臂的截面，H点为J点在水平面的投影，OH与x轴的夹角为大臂摆动角度q1，RJ与OH之间的夹角为大臂俯仰角度q2。钻臂运动学解算转化为：在已知大臂摆动角度q1和大臂俯仰角度q2的前提下，求解左右 2 个液压缸长度，即图2 中的EN和GM的长度LEN和LGM。

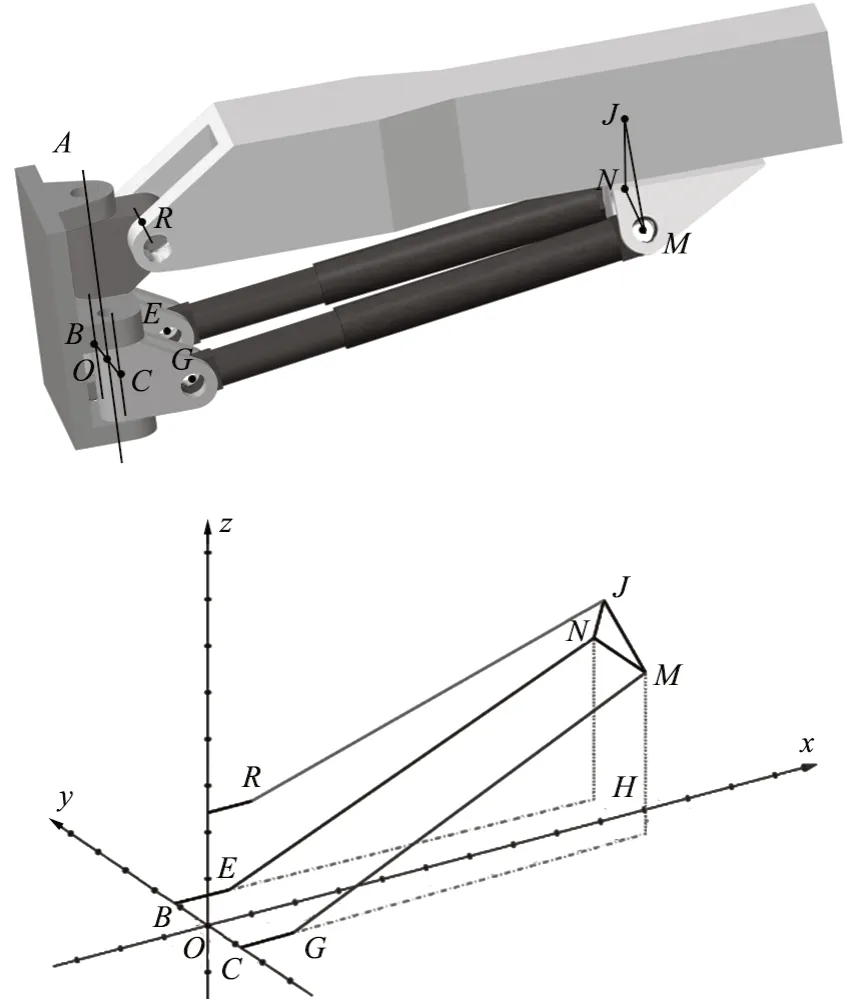
图2 凿岩机器人三角钻臂结构Fig.2 Triangular drilling arm structure of rock-drilling robot

J点位于大臂坐标系，可得J点坐标，

已知J点可计算出M点坐标，

式中：E0为初始状态的E点。

在△GIM中，可以求得IM的长度和GI的长度，最终可以求得GM的长度及EN的长度

1.3 钻臂支臂缸的 PID 控制

由式 (3) 可以根据关节变量q1、q2得到目标支臂缸长度。对目标支臂缸长度做闭环控制，可以实现支臂缸位置控制，支臂缸控制框图如图3 所示。

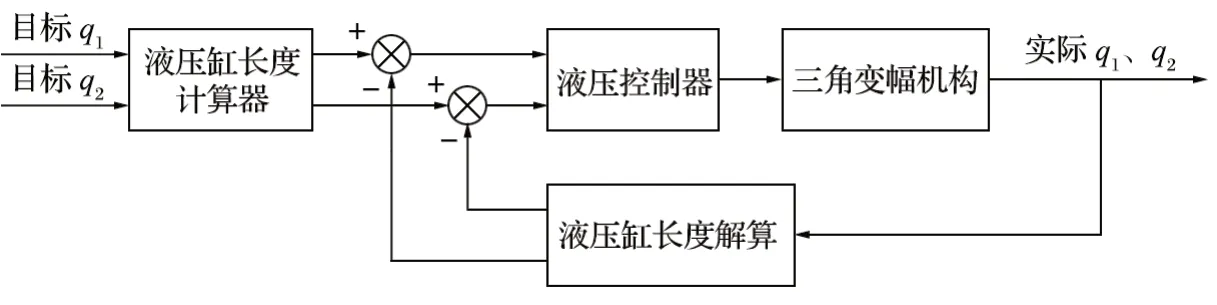
图3 钻臂支臂缸控制框图Fig.3 Block diagram of load arm cylinder control for drilling arm

考虑到液压系统具有较大的惯性质量，响应速度慢，流量会随负载分配，控制中采用速度、位置双闭环的控制方法[9]，控制框图如图4 所示。其中液压缸线速度可以通过对式 (3) 两边求导得到，如式 (5) 所示。内环是对液压缸线速度进行 PID 控制，目标线速度可以通过三次、五次多项式差值等方法得到；外环是对液压缸位置进行 PID 控制[10]。

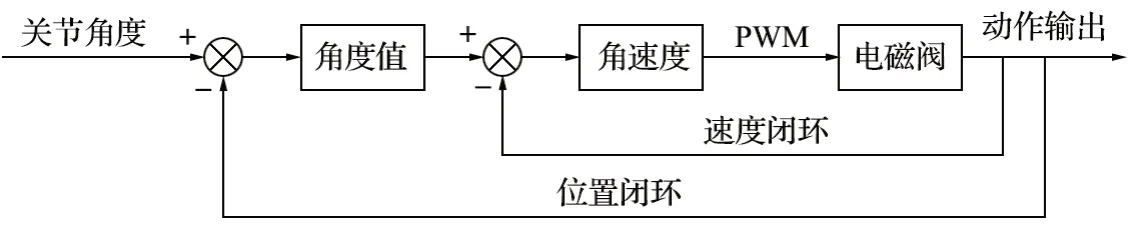
图4 双闭环控制框图Fig.4 Block diagram of double closed-loop control

2 机械臂动力学建模

该机械臂有 6 个自由度：大臂摆动角度q1、大臂俯仰角度q2、大臂伸缩长度q3、推进梁旋转角度q4、推进梁俯仰角度q5、推进梁伸缩角度q6，其运动需要使用q1～q6共 6 个参数来确定，设机械臂的角度矢量为

根据上节的运动学解算结果，利用拉格朗日方法[11]可以求出动力学模型：

根据现代控制理论，定义状态变量和机械臂的动力学模型的输入

式 (7) 可简化为

写成矩阵形式为[12]

式中：I∈R n·n为单位矩阵。

假设各个臂为质量均匀分布的连杆机构，

式中：M(q) 为各个臂的转动惯量与关节角度组成的矩阵，平移关节此项为 0；N(q,) 为各个臂的质量、关节角度和角速度组成的矩阵；G(q) 为各个臂的重力分量组成的矩阵。

机械臂参数如表1 所列。

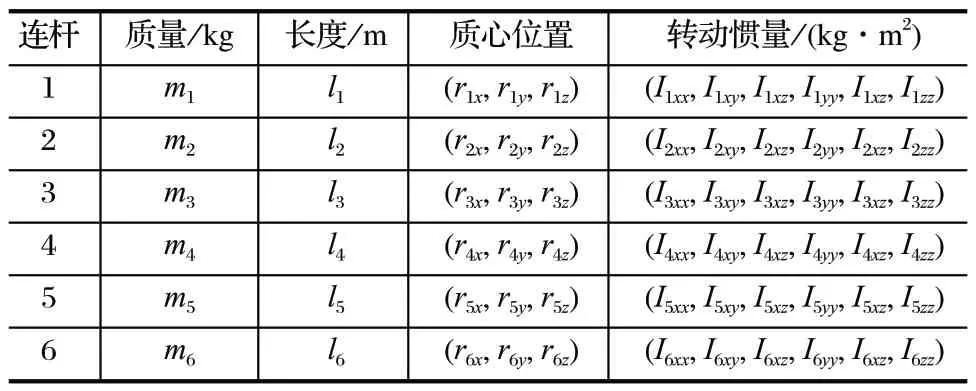
表1 机械臂参数Tab.1 Parameters of robotic arm

将表1 参数带入式 (13) 中可以求得各个系数。

在 Matlab 中使用机器人工具箱[13]建立所示机械臂模型，如图5 所示，可以得到 12×12 的矩阵A，12×6 的矩阵B，6×12 的矩阵C，6×1 的矩阵G。给机械臂的动力学参数赋予表1 中的数值，假设机械臂以角速度 5°/s 经过关节变量的零点，伸缩量维持 0 mm 不变，可得

图5 钻臂模型Fig.5 Drilling arm model

3 LQR 控制器设计

LQR[14]是线性二次型调节器的缩写，是一种反馈最优控制器。设计过程中要解决的问题是如何选取使代价函数值最小的状态量和控制量权重。笔者选取LQR 控制器主要是对机械臂平顺性进行研究，定义性能指标为表示机械臂位移、速度的加权平方和在时域的积分值。

LQR 方法给定了决定性能的目标函数

式中：Q为半正定的状态加权矩阵；R为正定的控制加权矩阵；x∈R12·12；u∈R12·1。

系统的期望性能由Q、R矩阵决定，针对不同工况选择不同的权重系数，求解出符合各自工况下的最优控制器。

设状态反馈控制率

式中：Ki为状态反馈增益矩阵；G为式 (7) 的重力分量，选取合适的数值把G抵消。

Riccati 方程为[15]

式中的A、B、Q、R都是已知的，可以求得P，进而求得闭环状态方程

得到本系统的最优控制矢量

最优控制矢量由模型参数和加权系数决定，而加权系主要靠设计者整定获得，这就使控制器性能存在较大的主观性。

3.1 单回路 LQR 控制器设计

采用 LQR 控制方法对凿岩机器人机械臂进行控制，根据其状态空间表达式利用 MATLAB 中的 lqr()函数计算出K1矩阵[16]。对于大臂伸缩、推进梁旋转、推进梁俯仰、推进梁伸缩的控制，由于他们之间不存在耦合关系，以推进梁俯仰为例，其控制框图如图6 所示。

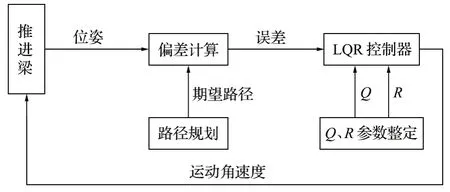
图6 推进梁俯仰控制框图Fig.6 Block diagram of pitching control for advancing beam

在 MATLAB Simulink 中搭建模型，如图7 所示。得到反馈 LQR 控制器的最优参数为K=[1.15 -2.51]。

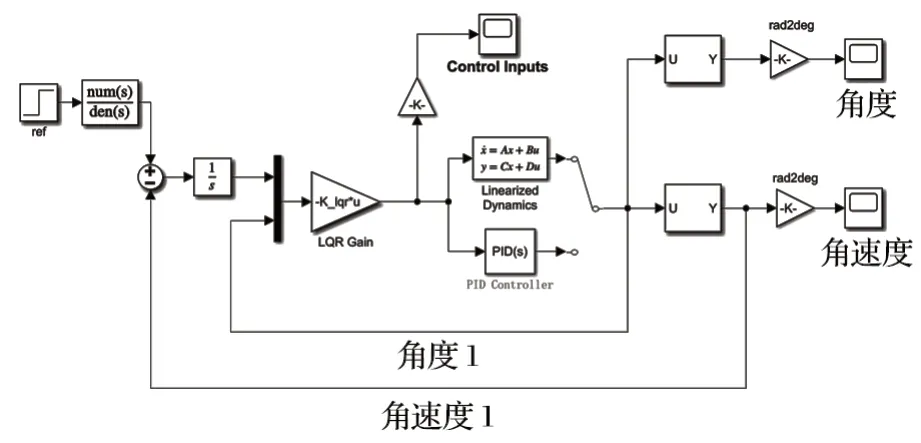
图7 推进梁俯仰 Simulink 仿真Fig.7 Simulink simulation of advancing beam pitching

3.2 多回路 LQR 控制器设计

由于单回路 LQR 控制器依靠一个单一的状态反馈矩阵对系统进行控制，对于耦合系统控制效果不佳，考虑将大臂摆动和俯仰解耦分开控制，实现两回路 LQR 控制[17-18]，两回路 LQR 控制结构如图8 所示。得到反馈 LQR 控制器的最优参数为K=[2.35-1.50 0.02 0.1]。

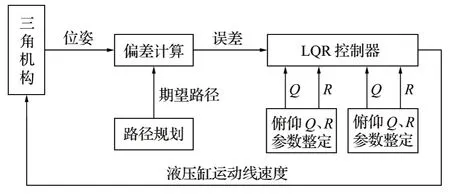
图8 三角钻臂运动控制框图Fig.8 Block diagram of motion control for triangular drilling arm

4 试验仿真分析

对于大臂伸缩、推进梁旋转、推进梁俯仰、推进梁伸缩的控制，将笔者设计的 LQR 控制器和 PID 控制进行对比，系统阶跃响应对比结果如图9 所示。

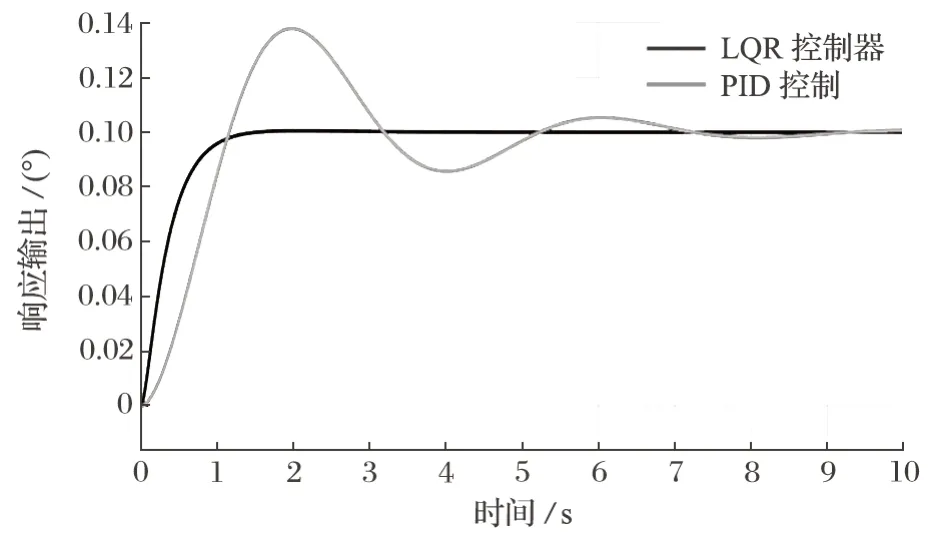
图9 推进梁俯仰 LQR 控制器和 PID 控制对比Fig.9 Comparison of LQR controller and PID control for advancing beam pitching

对于大臂摆动和俯仰的控制，将设计的 LQR 控制器和 1.3 节的 PID 控制进行对比，以左液压缸为例，系统的阶跃响应对比结果如图10 所示。

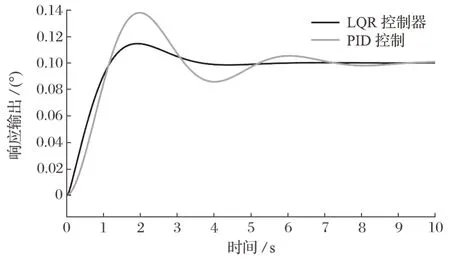
图10 臂架摆动 LQR 控制器和 PID 控制对比Fig.10 Comparison of LQR controller and PID control for arm support swing

将阶跃响应的结果进行整理，如表2 所列。

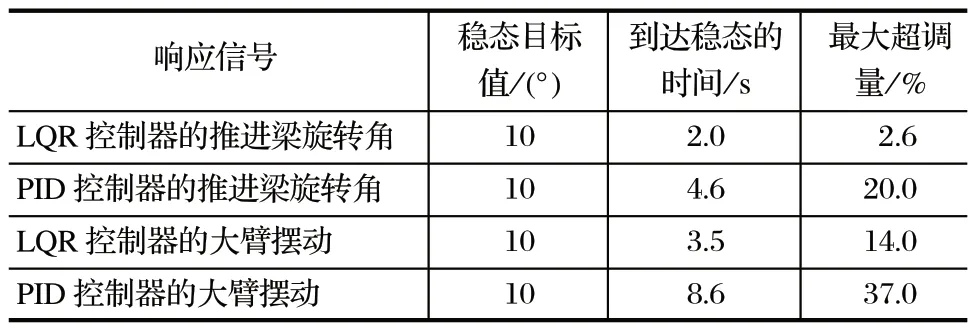
表2 机械臂响应结果Tab.2 Response results of robotic arm

由表2 可以看出，推进梁旋转角度 PID 控制器到达稳态的时间为 4.6 s，使用 LQR 控制器后到达稳态的时间仅为 2.0 s，效率提高 1 倍，柔性机械臂的定位速度大幅提升。

对于大臂摆动和俯仰的控制，经过解耦之后控制左右 2 个液压缸的长度。图10 所示为控制左液压缸长度的曲线，PID 控制存在较多的峰值，在作业过程中会造成大臂的抖动，进而影响作业精度，而 LQR控制在相应过程中只存在 1 个峰值，随后误差会逐渐趋近 0，说明经过 LQR 控制的系统自动调节平衡能力要强于 PID 控制，这对于机械臂起到了较好的保护作用。

单回路 LQR 控制的机械臂的跟踪曲线如图11 所示。图11 中目标角度变化过程中，控制误差基本能够维持在 0°，跟踪过程中角速度的误差＜0.01°/s。

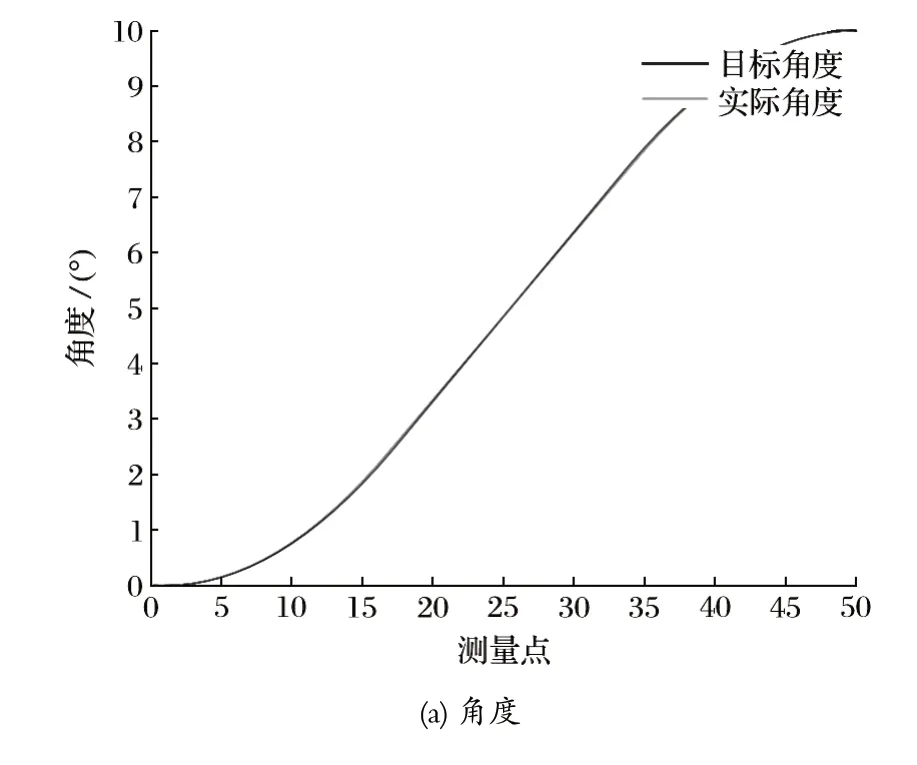
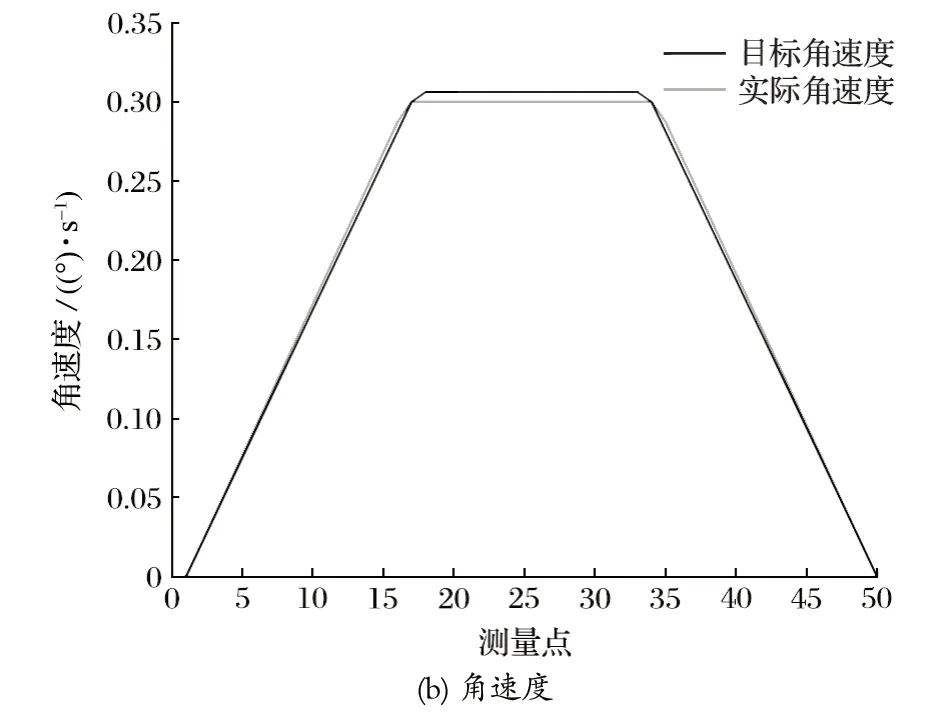
图11 推进梁俯仰 LQR 跟踪控制Fig.11 LQR tracking control of advancing beam pitching

双回路 LQR 控制的机械臂的跟踪曲线如图12所示。图12 中目标角度变化过程中，控制误差基本＜0.5°，跟踪过程中角速度的误差＜0.5°/s。

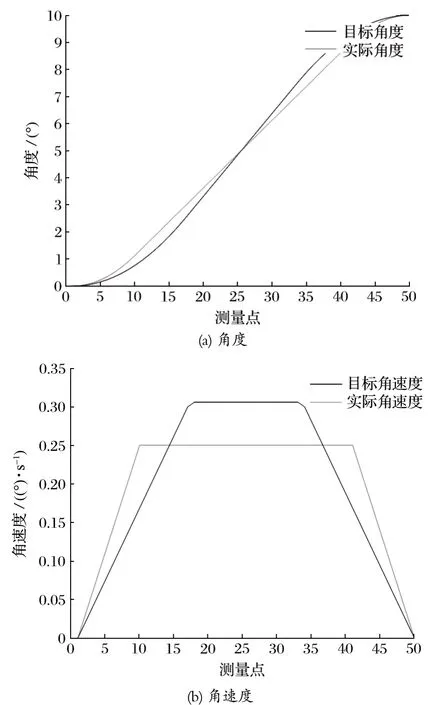
图12 大臂摆动 LQR 跟踪控制Fig.12 LQR tracking control of main arm swing

5 实车验证

采用徐工某型号凿岩机器人对文中的算法进行了验证，如图13 所示。

图13 某型号凿岩机器人Fig.13 A certain type of rock-drilling robot

给定机械臂大臂摆动、俯仰、伸缩，推进梁俯仰、摆动关节初始值为 [0° 0° 0 mm 0° 0°]，目标值为 [18° -32.4° 100 mm 14.4° -36°]，利用梯形轨迹公式进行关节空间轨迹计算后得到各部分角度/长度变化数据，如表3 所列，角/线速度变化数据如表4 所列。

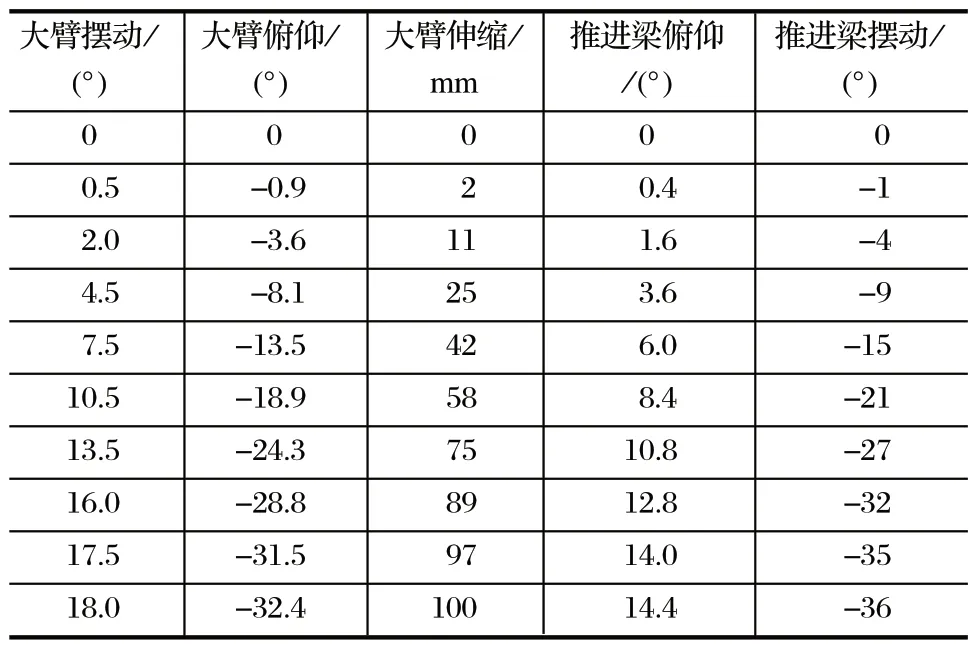
表3 各关节角度/长度变化Tab.3 Changes in joint angles/lengths

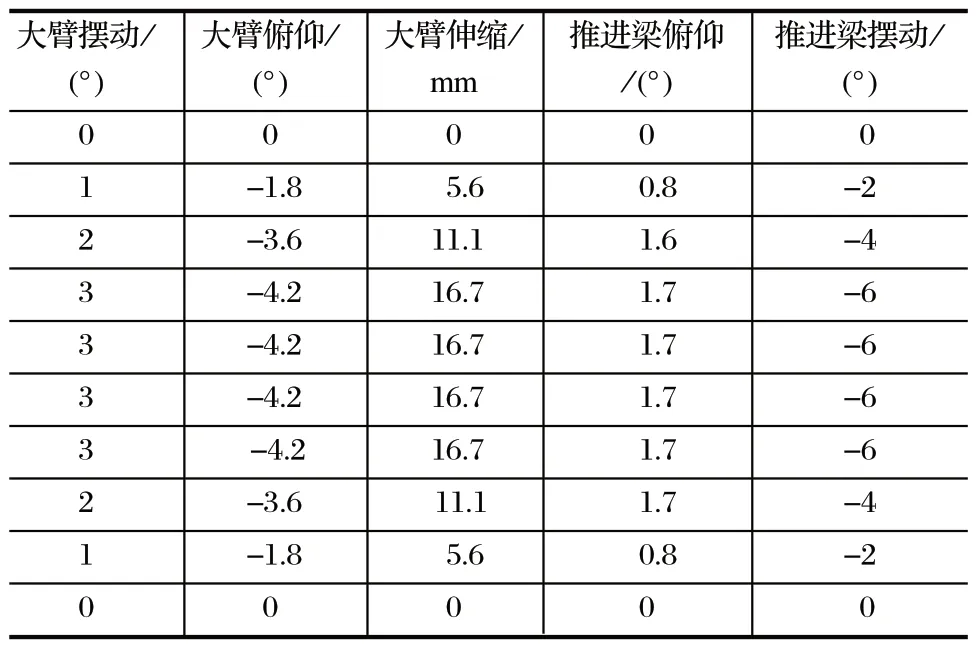
表4 各关节角速度/线速度变化Tab.4 Changes in angular velocity/linear velocity of each joint

使用 PEAK CAN 记录控制过程中大臂俯仰、推进梁摆动角速度变化曲线，如图14、15 所示，关节角度基本能与理论角度对应上。

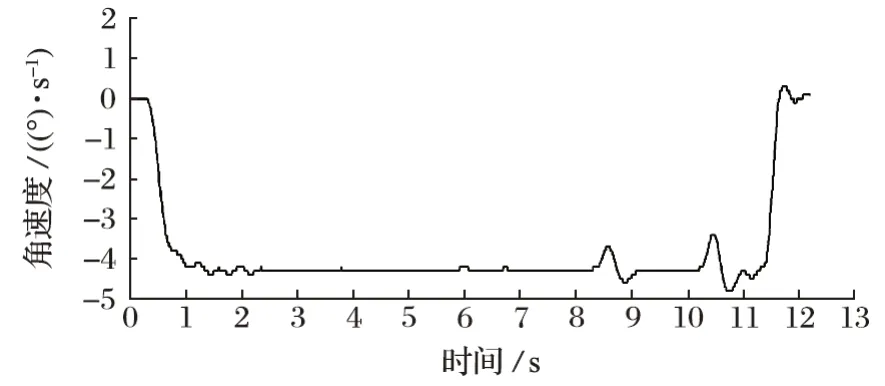
图14 大臂俯仰角速度变化曲线Fig.14 Change curve of pitching angular velocity of main arm

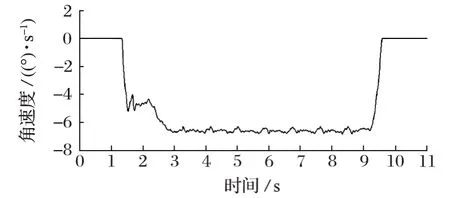
图15 推进梁摆动角速度变化曲线Fig.15 Change curve of swing angular velocity of advancing beam

6 结语

对凿岩机器人机械臂运动学和动力学进行了研究，通过运动学分析三角钻臂，解耦了大臂摆动和大臂俯仰运动，并对三角机构使用 PID 进行控制。通过动力学分析，得到机械臂各关节的动力学方程，进而建立机械臂的状态空间方程。根据机械臂运动特点提出一种基于线性二次最优控制 (LQR) 的控制方法，并与 PID 控制进行仿真对比，结果表明，该方法能够提高机械臂的定位精度，减小机械臂移动过程中的冲击、抖动，并将该方法应用到徐工某型号凿岩机器人机械臂控制中，取得了良好的效果。研究结果可为凿岩机器人控制提供有效帮助，为隧道施工提供更多的支持。