基于本征正交分解降阶的燃耗计算方法研究

张彬航,毕彦钊,龚瀚源,张永红,*,袁显宝

(1.三峡大学 机械与动力学院,湖北 宜昌 443002;2.三峡大学 理学院,湖北 宜昌 443002)

数值反应堆技术基于高性能计算和多物理耦合实现对堆芯各种物理现象的精细刻画,能够准确预测反应堆在服役过程中的关键安全参数,为先进核能系统的研究开发和安全分析提供了重要手段和依据[1-3]。反应堆燃耗计算是实现数值反应堆精细模拟的关键环节。燃耗计算通过求解燃耗方程获得燃料同位素及裂变产物成分随时间的演变过程,不但会通过改变燃耗区的核素种类及密度影响中子输运过程,也为热工水力计算提供总功率及各燃耗区的实际功率。在高保真燃耗计算中,根据目标问题的实际规模,燃耗区数量可达数十万甚至上百万,需要逐个计算和存储各燃耗区的相关参数,包括中子通量密度、反应截面、功率等物理量,导致计算时间和存储开销显著增加[4-5]。即使借助高性能计算机的并行能力,全堆芯高保真模拟也需要数百核时的计算时间及数百GB的存储开销,计算成本显著增加,同时难以获得高保真模型实时求解所需的加速效果[6-7]。

近年来,为了减少高保真燃耗计算中的存储开销,提高计算效率,主要围绕以下两个方面开展研究工作。一是通过先进的理论模型和并行计算方法提高上游中子输运计算和热工水力计算的效率和精度[8-9],为燃耗计算提供精确的中子学参数;二是针对反应堆燃耗计算中的物理过程和特点,开展了包括点燃耗计算方法[10]、燃耗链压缩方法[11]、输运-燃耗耦合计算方法[12]、并行计算方法[13]、模型降阶方法等多方面的研究。尽管高保真堆芯物理模型对计算成本有较高要求,但模型降阶方法提供了解决途径。常见的模型降阶方法包括本征正交分解(POD)、特征广义分解(PGD)、缩减基方法(RBM)等。其中通过POD方法得到的降阶模型自由度低、数据存储量小,且为原系统的最佳逼近,在高维复杂系统的计算效率及精度等方面具有显著优势[14]。该方法在中子输运/扩散计算[15]、热工水力计算[16]、堆芯功率在线监测[17]等方面得到了广泛的研究与应用,取得了良好的加速效果,但在高保真燃耗计算方面,国内尚处于起步阶段[18]。

本文基于POD方法,通过建立高保真燃耗计算的参数化降阶模型,以1组正交基函数实现对各燃耗矩阵的快速构造。进一步基于离线-在线数值求解策略,通过选用JAEA发布的MOX燃料栅元基准题进行计算分析,初步验证本方法的正确性和可行性。

1 模型降阶方法

1.1 POD方法

POD方法通过全阶模型的仿真数据或实验数据构建自相关矩阵,求解自相关矩阵的特征向量获得降阶模态,并将全阶模型投影到数个最大特征值对应降阶模态张成的子空间上以达到降阶目的。

g≪n

(1)

式中:ai(t)为模态系数;g为由全阶模型模态能量占比截断后的模态数;φi(x)为模态正交基。

实际上,POD降阶过程是将全阶模型不同时刻的响应y(x,ti)与其在该正交基张成的子空间Φ上的投影误差范数等效为一个最值问题[19]:

(2)

式中:(·,·)为Hilbert空间上的内积;‖·‖2为L2范数的平方;I(n)为n阶单位矩阵;G为响应y(x,ti)在子空间Φ上投影平方的最大值。

进一步可将式(2)的最值问题转换为特征值求解问题:

(3)

式中:S为自相关矩阵,S∈Rm×m;λi为S的第i个特征值;Y为全阶模型不同时刻的响应集合。由式(3)获得模态正交基后利用式(1)即可完成全阶模型的降阶。

1.2 奇异值分解

由1.1节可知,POD方法的关键在于确定1组合适的正交基。本文利用奇异值分解(SVD)进行求解,该方法广泛用于降维算法中的特征分解。奇异值分解和特征分解不同,并不要求待分解的矩阵为方阵。对1.1节中的矩阵Y进行SVD分解,可得:

(4)

由奇异值分解过程,结合式(3)和式(4)可得:正交矩阵U的前r列构成矩阵Y中列空间的标准正交基;正交矩阵V的前r列构成矩阵Y中行空间的标准正交基。因此,正交基Φ=Um×r=(φ1,φ2,…,φr)。

为了尽可能少地利用模态正交基完成式(1)中y(x,ti)的逼近,可以通过模态能量占比E(g)进行模态截断。E(g)定义为前g个特征值和与总特征值和的比值,用来衡量各模态的还原能力:

(5)

式(5)中,自相关矩阵S的特征值与各奇异值存在如下关系:

(6)

E(g)越接近1,表明模态基函数所包含原全阶模型的特征信息越完整。通常E(g)应大于0.95,对应所截断的模态基函数可将原系统投影到更低维的子空间上,实现模型降阶。

2 参数化燃耗降阶模型构建方法

2.1 参数化燃耗降阶模型

反应堆内燃料中核素成分随时间的变化情况可用燃耗方程组描述,其矩阵形式及解为:

(7)

式中:N(t)为核素的密度向量;A为燃耗矩阵,由系统中所有核素的反应率和衰变率构成;N(0)为初始时刻的核素密度;t为时间。矩阵A可进一步表达为如下形式:

A=Ar+Ad

(8)

式中:Ar为燃耗系数矩阵,其矩阵元由中子通量密度和微观反应截面的乘积构成;Ad为衰变矩阵,其矩阵元由衰变常量与衰变分支比的乘积构成,在整个燃耗过程中该矩阵不变。

由POD降阶方法可将Ar和中子通量密度φ用两组正交基函数表示:

(9)

式中:an、bn为待定的模态系数;r1、r2为模态阶数;ξn、φn为模态正交基。

在燃耗计算过程中需要对各燃耗区的Ar进行反复计算和存储,计算成本较高。将φ作为输入参数,可得Ar的参数化形式:

Ar=f(φ)

(10)

由式(9)和式(10)可进一步得到φ与Ar的映射关系,即参数化燃耗降阶模型:

(11)

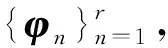
2.2 模态基函数构造方法

(12)

式中:m1为瞬态快照Ak的维数;m2为中子能群数;SAr∈Rm1×n;Sφ∈Rm2×n;n为快照矩阵的采样长度,由燃耗区数、燃耗深度、功率水平等输入参数确定。

对快照矩阵SAr与Sφ进行奇异值分解可得:

(13)

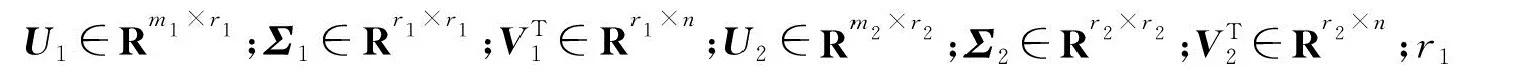
由奇异值分解可知,左奇异矩阵U1和U2中的列向量即为原矩阵列空间内的1组标准正交基,即:

(14)

对于燃耗系统在t时刻的中子通量密度φt和燃耗系数矩阵At,根据实际计算精度要求进行模态能量截断得到降阶模态数r后,基于式(9),可将At和φt表示为:

(15)

式中:U1,cut=(ξ1,ξ2,…,ξr),U1,cut∈Rm1×r;U2,cut=(φ1,φ2,…,φr),U2,cut∈Rm2×r。

将SAr降阶后的右奇异矩阵V1,cut左乘Sφ得到1组新的中子通量密度基函数Sψ:

(16)

式中:vn,r为矩阵V1,cut中第n行r列的矩阵元;Sψ∈Rm2×r。

(17)

进一步通过参数化燃耗降阶模型,得到φt与对应系数矩阵At的映射关系:

U1,cut(c1σ1,c2σ2,…,crσr)T

(18)

最后由式(15)和式(18)可得:

an=cnσnn=1,2,…,r

(19)

3 离线-在线计算策略

基于参数化燃耗降阶模型进行燃耗计算可分为离线和在线两个阶段:离线阶段完成模态基函数的构造;在线阶段基于离线阶段预先存储的数据,通过简单的代数运算获得中子通量密度对应的燃耗系数矩阵。

3.1 离线阶段

离线阶段计算流程如图1所示:1) 根据目标问题的代表性参数确定快照矩阵的采样长度,通过中子输运-燃耗计算获得燃耗系数矩阵和中子通量密度构成的快照矩阵SAr和Sφ(式(12)),同时保存衰变矩阵Ad;2) 基于POD方法分别获得快照矩阵SAr和Sφ的奇异矩阵和奇异值(式(13));3) 根据计算要求进行模态能量截断确定降阶模态数(式(5)),构造燃耗系数矩阵和中子通量密度的模态基函数U1,cut和Sψ(式(15)和式(16));4) 存储模态基函数U1,cut、Sψ及衰变矩阵Ad。

图1 离线阶段计算流程图Fig.1 Flow chart of offline phase

3.2 在线阶段

在线阶段计算流程如图2所示:1) 进行中子输运计算获得中子通量密度φ,无需统计和存储各燃耗区各核素的微观反应率;2) 基于离线阶段预先存储的模态基函数,将φ投影至Sψ上获得还原燃耗系数矩阵的模态系数(式(19));3) 基于离线阶段预先存储的衰变矩阵Ad,完成对燃耗矩阵A的构造(式(8));4) 基于燃耗矩阵A求解燃耗方程,完成当前燃耗步长计算,返回第1步进行下一个燃耗步长的计算,直至步长末。

图2 在线阶段计算流程图Fig.2 Flow chart of online phase

4 数值验证

为验证基于POD降阶的燃耗计算方法的正确性和有效性,本文选用JAEA发布的MOX燃料栅元基准题进行计算分析,该基准题的平均卸料燃耗深度为70 GW·d/t,功率密度为36.6 W/gHM,几何模型如图3所示,包括3个材料填充区域,由内至外分别为燃料、包壳和慢化剂,详细材料及工况信息参见文献[20]。该基准题提供了16种燃耗计算程序的计算结果,包括无限增殖因数、部分重核及裂变产物的核素密度等参考值,并以这些结果的平均值加减两倍标准差作为置信区间。本文计算程序选用自主研发的燃耗计算程序AMAC[21],燃耗数据库选用JAEA提供的简化燃耗链,包括21个重核、49个裂变产物和1个伪核素,该简化燃耗链在轻水堆燃耗计算中得到了广泛的验证与应用[22]。

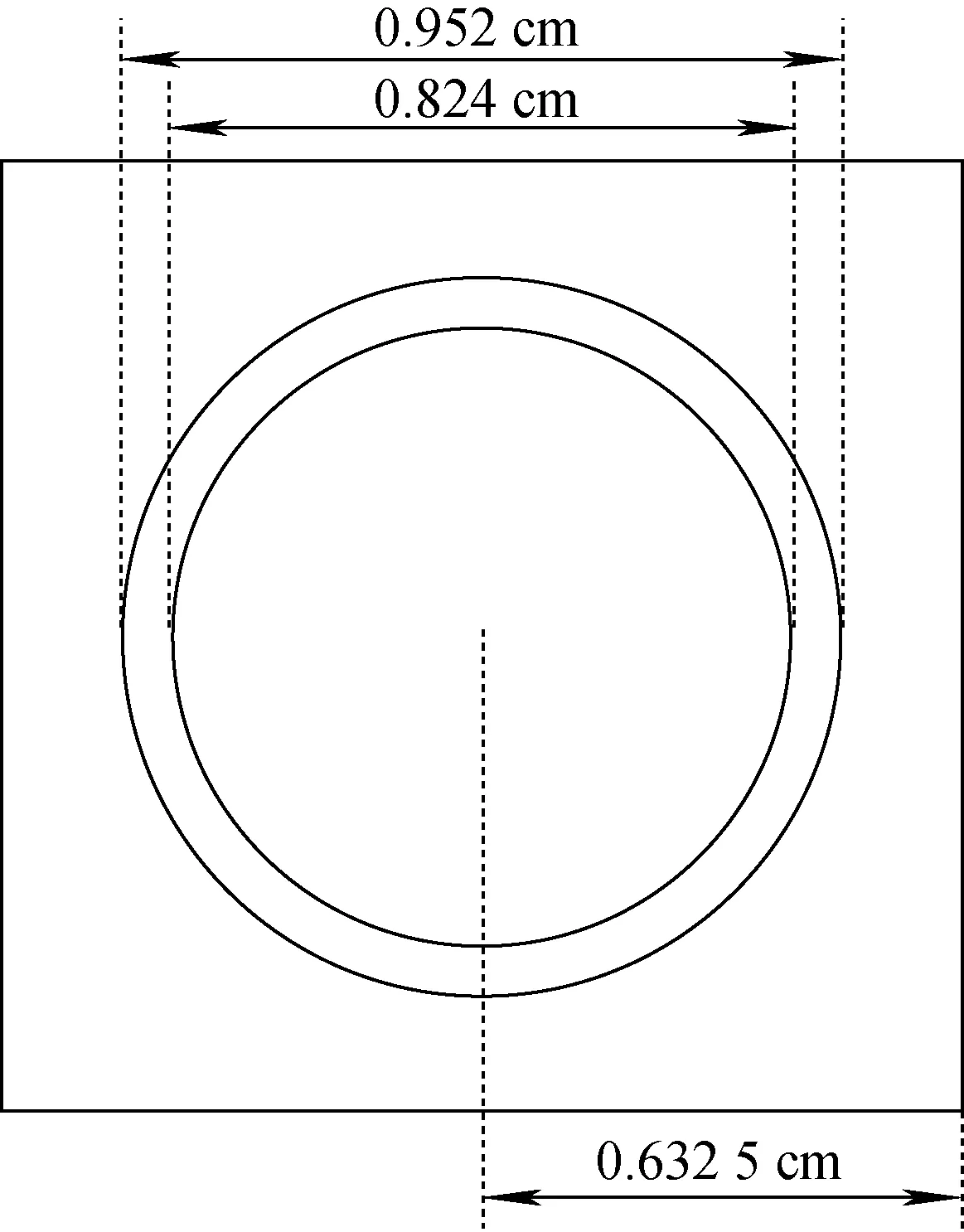
图3 MOX燃料栅元几何示意图Fig.3 Geometrical configuration of MOX fuel pin cell

4.1 无限增殖因数

该基准题提供了0、0.1、5、10、15、20、30、50和70 GW·d/t共计9个燃耗深度下的基准值。本文共计划分35个燃耗步长:第1个步长为0.1 GW·d/t;第2个步长为1 GW·d/t,并以1 GW·d/t为步长间隔递增至第11个步长10 GW·d/t;第12个步长为12.5 GW·d/t,并以2.5 GW·d/t为步长间隔递增至第35个步长70 GW·d/t。径向对燃料区等体积划分3层。图4示出基于MOX燃料栅元建立全阶燃耗模型计算的无限增殖因数kinf及与其他16种计算程序计算结果平均值的相对偏差。由图4可知,本文计算的kinf均在平均值的置信范围内,与平均值的相对偏差在整个燃耗过程中始终小于100 pcm。计算结果验证了AMAC对该基准题计算的正确性。

图4 MOX燃料栅元kinf的计算结果Fig.4 Calculation result of kinf for MOX fuel pin cell

进一步基于本文提出的参数化燃耗降阶模型对全阶模型进行降阶。在离线阶段以模态能量占比E(g)≥0.99进行模态截断,分别获得燃耗系数快照矩阵(SAr∈R5 041×105)和中子通量密度快照矩阵(Sφ∈R107×105)前50阶的模态基函数U1,cut和Sψ。在线阶段的计算过程中无需统计和存储各燃耗区中核素的反应率信息,采用32阶最佳一致逼近多项式方法求解燃耗方程[23],并以全阶模型的计算结果作为参考值。

图5示出采用不同模态基函数计算的kinf及与全阶模型kinf相对偏差随燃耗深度的变化,同时以基准题提供的16种计算程序计算结果平均值的正负两倍标准差作为置信区间。由图5可知,当采用1阶模态基函数进行模态还原时,kinf与全阶模型的相对偏差均在500 pcm以下,说明该模态基函数已包含了全阶燃耗模型的主要特征信息,具有良好的模态还原能力。采用5阶降阶模型计算时,kinf与全阶燃耗模型的相对偏差减少至100 pcm以内。继续提高模态阶数至10阶时,可以发现kinf与全阶模型的相对偏差已非常小,皆在5 pcm以内。考虑到20、30、40和50阶降阶模型计算的kinf与全阶模型在各燃耗步长的相对偏差皆小于5 pcm,因此在图5中并未展示。总体而言,通过不同模态阶数构造的降阶模型与全阶模型的计算结果相比,对于kinf的计算皆具有良好的精度。

图5 不同模态截断下kinf的计算结果Fig.5 Calculation result of kinf with different basis functions

4.2 核素密度

基准题提供了17个重核和12个裂变产物的核素密度。图6示出29个核素在燃耗过程中相对于全阶模型的平均相对偏差。由图6可知,随阶数的提高,所有核素密度的相对偏差逐渐降低。1阶降阶模型的计算精度较差,大部分裂变产物的平均相对偏差大于10%。5阶降阶模型得到的大部分核素密度的相对偏差低于1%,其中核素245Cm的相对偏差达到3.74%。10阶降阶模型的相对偏差已全部低于0.1%。

图6 29个核素密度的平均相对偏差Fig.6 Average relative deviation of 29 nuclide densities

本文进一步选取了核素235U、239Pu、155Gd和149Sm进行详细分析,以全阶模型的计算结果作为参考值,以16种计算程序计算结果平均值的正负两倍标准差作为置信区间。图7示出235U、239Pu、155Gd和149Sm 4种核素的核素密度及相对偏差随燃耗深度的变化。

图7 不同模态截断下核素密度的计算结果Fig.7 Calculation result of nuclide density with different basis functions

由图7a和图7b可知,对于重核核素235U和239Pu,基于降阶模型得到的核素密度随燃耗深度的变化趋势与全阶模型相同,且皆在基准值的置信区间内。在燃耗深度为5 GW·d/t时,通过1阶降阶模型计算得到的235U 核素密度的相对偏差达到最大值,为4.175%。随着模态阶数的提高,5阶和10阶降阶模型的计算精度远高于1阶降阶模型,其相对偏差在整个燃耗过程中分别始终低于0.1%和0.005%。当模态阶数进一步提高到20～50阶时,通过相应降阶模型计算得到的235U和239Pu的核素密度与10阶降阶模型的计算精度相当,约在0.005%以内。

如图7c和图7d所示,基于降阶模型得到的155Gd和149Sm的核素密度随燃耗深度变化的趋势落在基准值的置信区间内。寿期初155Gd和149Sm的核素密度快速增长,与全阶模型计算结果相比,通过1阶降阶模型得到155Gd和149Sm的核素密度相对偏差分别为16.645%和16.549%。随燃耗的加深,155Gd和149Sm的相对偏差先减小后增加,寿期末的相对偏差分别为11.996%和4.519%。虽然1阶降阶模型对于155Gd和149Sm的计算相对偏差较大,但其核素密度的量级较小,因此对1阶降阶模型计算kinf的精度影响较小。表1列出不同模态截断下155Gd和149Sm的核素密度与全阶模型计算结果的相对偏差。当采用5阶降阶模型时,整个燃耗过程中155Gd和149Sm的核素密度相对偏差始终小于5%,处于合理的误差范围内。进一步提高模态阶数至10阶,155Gd和149Sm的核素密度与全阶模型的相对偏差在0.1%以内。可见对于155Gd和149Sm这些具有较大中子吸收截面的核素,仅采用1阶降阶模型还难以精确获得核素密度随燃耗深度变化的计算结果,需要采用更多的模态基函数。相比于1阶降阶模型,5阶和10阶降阶模型对于核素密度的计算具有更好的精度。

表1 不同模态截断下155Gd和149Sm核素密度的相对偏差Table 1 Relative deviation of nuclide density of 155Gd and 149Sm with different basis functions

4.3 计算效率与存储开销

燃耗计算的耗时主要包括系数矩阵构建、燃耗方程求解及数据更新传递3部分。表2列出不同阶数下各降阶模型和传统燃耗的计算时间。由表2可见,采用降阶模型构建系数矩阵的最大加速比为82.56,整个燃耗计算耗时的最大加速比为18.23。相比于传统计算方法,降阶模型在在线阶段无需统计通量归一因子和各燃耗区内各核素的单群反应率,减少了数据传递时间,提高了计算效率。由于不同阶数的降阶模型仅影响系数矩阵的精度和构建时间,并不影响系数矩阵的规模,因此随着降阶模型阶数提高,燃耗方程的求解耗时不变。

表2 燃耗降阶模型的计算耗时Table 2 Calculation time of burnup reduced-order model

燃耗计算的内存开销包括定义数据和统计数据[7]。定义数据包括燃耗步长、功率密度、各燃耗区的通量、核素密度、截面信息等。统计数据主要指计算过程中更新及存储的数据。在对本文算例的计算过程中,定义数据包括各燃耗区存储长度为107的通量数组和长度为71的核素密度数组。此外还需存储每个核素的4种反应截面:裂变截面、俘获截面、(n,2n)截面、(n,3n)截面,上述数据皆为双精度型。统计数据主要包括用于燃耗方程求解中的稀疏矩阵。燃耗系数矩阵采用三元组存储,由于非零元素为1 182个,因此需要2个长度为1 182的整型数组和1个长度为1 182的双精度型数组。同时对于各燃耗区共用的衰变矩阵,需要2个长度为84的整型数组和1个长度为84的双精度型数组。

表3列出不同阶数下各降阶模型的内存开销及相对于传统燃耗计算的内存占比。当采用降阶模型时,内存开销主要由奇异值、通量基函数和系数矩阵基函数所决定。由表3可知,随着阶数提高,内存占比逐步提高。即使采用50阶降阶模型进行计算,其内存开销仍为传统燃耗计算的34%。燃耗降阶模型对内存开销的节省效果较为显著。

表3 燃耗降阶模型的内存开销Table 3 Memory requirement of burnup reduced-order model

由4.1节和4.2节可知,当采用5阶降阶模型时:在计算精度方面,kinf的相对偏差在整个燃耗过程中始终低于100 pcm,所有核素密度的相对偏差均低于5%,大部分核素密度的相对偏差低于1%;在计算成本方面,5阶降阶模型的加速比为17.26,内存开销为传统燃耗计算的5%。随着阶数进一步提高,高阶降阶模型对计算精度和效率的提升已十分有限,但内存占比会逐步增加。因此对于降阶模型阶数的选择,在满足计算精度的条件下,应充分考虑内存开销的影响,以获得计算精度、效率和内存开销间的平衡。

5 结论

本文基于POD方法,建立了高保真燃耗计算的参数化降阶模型,实现了对燃耗矩阵的快速构造。进一步基于“离线-在线”计算策略,选用JAEA发布的MOX燃料栅元基准题对本方法进行了初步验证与分析,结论如下。

1) 对于kinf的计算,仅需通过1阶降阶模型便可获得与全阶模型相对偏差小于500 pcm的计算精度;对于29个核素的计算,由5阶降阶模型得到的大部分核素密度的相对偏差低于1%。进一步重点分析了核素235U、239Pu、155Gd和149Sm。对于重核235U和239Pu的核素密度计算,1、5和10阶降阶模型的相对偏差在整个燃耗过程中分别在5%、0.1%和0.005%以内;但对于中子吸收截面较大的核素155Gd和149Sm,1阶降阶模型的计算精度较差,5阶降阶模型的相对偏差在5%以内,10阶降阶模型的相对偏差可达到0.1%以内。

2) 相比于传统燃耗计算方法,不同降阶模型获得的加速比最大可达18.23。相比于传统燃耗计算,5阶降阶模型的加速比可达17.26,提高了计算效率。

3) 燃耗降阶模型无需计算和存储各燃耗区内各核素的反应截面、反应率等参数信息,同时能够减少统计数据的内存开销。5阶降阶模型能够在获得良好计算精度和效率的同时,内存开销仅为传统燃耗计算的5%。

本文仅对高保真燃耗计算的参数化降阶模型的正确性和可行性做了初步研究和分析。未来将进一步研究通过少量基函数完成一定规模燃耗区的矩阵构建方法,以显著降低全堆芯高保真燃耗的存储开销,提高计算效率。同时在离线阶段将计算规模控制在单栅元或超栅元阶段,以减少离线阶段的计算成本。