S油田纵波速度随不同储层参数的变化规律研究

＊刘励云 鲍祥生 曹向阳 王剑 陈国民 陈泽涛

（1.中国海洋石油国际有限公司 北京 100028 2.广东石油化工学院 广东 525000）

时移地震技术，它是利用不同时间采集的地震资料、动态资料等来进行油藏研究的一项技术，源于20世纪70年代中期，经过几十年的发展，已被国内外认为是一种较好认识剩余油分布、识别死油区、提高油田采收率等方面的一项重要技术[1-2]。S油田属于海上油田，包括两个重要的油藏，一个是P油藏，为上部油藏；另一个是下部油藏，为B油藏。依据测井特征的差异，P油藏垂向上主要包括2E、2D、2BC三个储层，B油藏垂向上主要包括Upper B和Lower B两个储层。为提高时移地震技术的应用效果，S油田目前采用先进的OBN采集技术进行时移地震数据采集，OBN采集技术是一种采用布设于海底的节点地震仪来独立采集、记录地震信号，受海况及周围环境影响小，能获得高质量地震资料。S油田采集时移地震数据包括2015年基础资料和2018年监测资料，对获得的时移地震资料进行常规处理和时移地震匹配处理后获得较好的时移地震差异数据，但对时移地震差异数据的解释面临一些困难，影响S油田对时移地震差异数据的运用，从而限制时移地震数据在油藏管理中发挥更大作用。要更好地认识S油田时移地震差异，对储层开展地震波速度随不同储层参数变化的规律性研究非常重要，因为地震波速度变化规律性的认识将为S油田时移地震差异解释提供理论支撑。

1.S油田不同储层特征

表1为S油田各储层平均参数，从表1可看出，各储层净毛比差异有大有小，差异最大是Upper B与2EF，平均净毛比差异达到0.51；各储层平均孔隙度差异不是很大，不同储层之间最大孔隙度差异是0.03；各层平均渗透率有相对好的，也有相对差一些的，2D和Upper B两个储层渗透率相对好些，分别达到了818mD和913mD，而2EF渗透率相对差一些，只有369mD；各储层平均厚度方面，Upper B储层厚度达到55.84ft，2EF储层厚度最小，只有4.91ft；各储层变异系数方面，2BC储层达到3.20，属于5个储层中变异系数最大，反映该储层内部不同砂体之间表现出较强的非均质性，Upper B和2D两个储层分别是1.15和1.21，属于5个储层中变异系数相对较小的，也反映出这两个储层内部不同砂体非均质性程度不及其他储层。

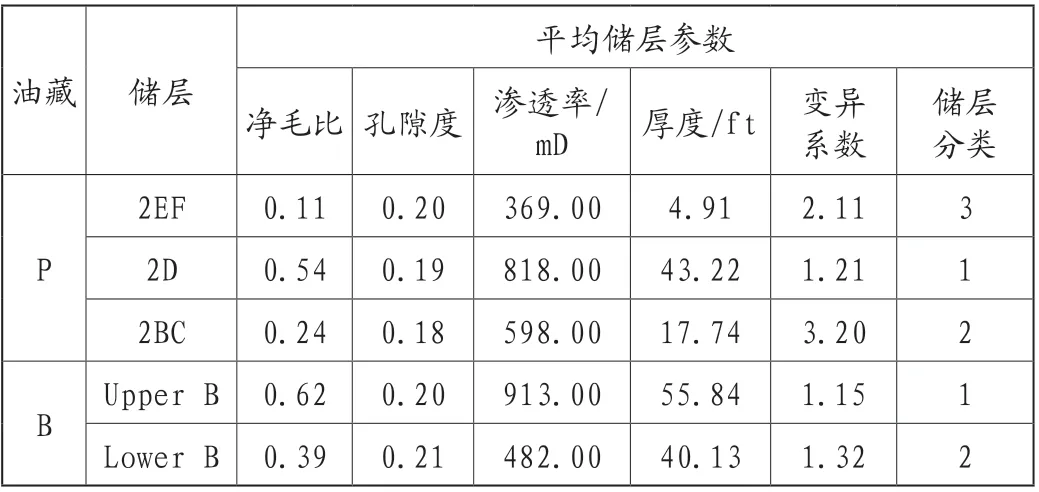
表1 S油田各储层平均储层参数

依据净毛比参数、渗透率、储层厚度、变异系数四个参数所处范围不同，S油田已建立如表2所示储层分类标准。依据表2储层划分标准，S油田5个主要储层中，其中2D和Upper B两个储层属于1类储层，2BC和Lower B两个储层属于2类储层，2EF属于3类储层。

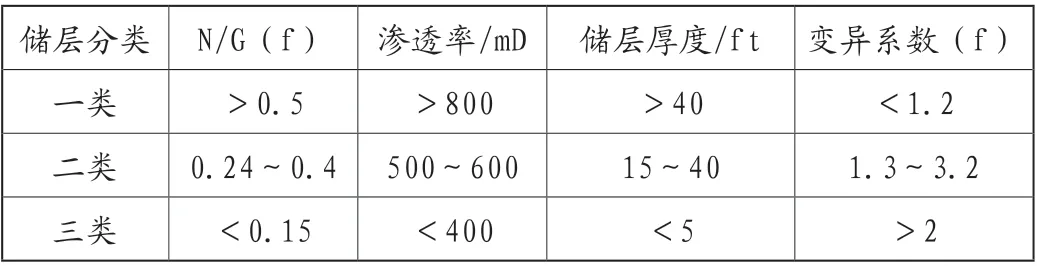
表2 S油田研究区储层分类标准

由表1可算出各储层的平均砂体厚度，其中2EF和2BC分别只有0.16m、1.3m，而2D、Upper B和Lower B分别为7.11m、10.55m、4.77m，对其进行研究对实际应用价值更大，因此后面储层参数分析研究主要针对2D、Upper B、Lower B储层来开展。

2.理论基础

从目前的文献[3-10]来看，关于地震波速度的研究理论目前已有很多，比如基于Wyllie方程的地震波速度求取[4]，基于Han经验关系的地震波速度求取[4]，基于Gassmann方程的地震波速度求取[5]，基于Raymer-Hunt-Gardner经验关系的地震波速度求取[6]。Wyllie方程比较适用于室温条件下的中等孔隙度范围纯净砂岩速度预测；Han经验关系适用于一定围压和孔隙压力条件下砂泥岩速度预测；Raymer-Hunt-Gardner经验关系一般只在估算低孔隙度地区有一定适用性。相对Wyllie方程和Han经验关系、Raymer-Hunt-Gardner经验关系等，基于Gassmann方程在地震波速度求取方面灵活性方面更好，可以依据油藏温压条件来计算地震波的速度，因此本文选择以Gassmann方程为基础的理论来计算地震波速度。

1951年，Gssmann通过研究形成了流体饱和岩石的有效体积模量计算方程[5]，该方程可用公式（1）来表示。

式中，kG是流体饱和岩石的体积模量；Kdry是干燥岩石的体积模量；Kma是基质的体积模量；φ是孔隙度；Kf是流体的体积模量。

基于Gassmann方程的纵横波速度可用公式（2）和公式（3）来计算。

式中，Vp、Vs分别为流体饱和岩石的纵波速度和横波速度；μdry为流体饱和岩石的剪切模量；ρ为流体饱和岩石的密度。

(1)关键体积模量求取

在Gassmann方程中涉及Kma、Kf、Kdry三个重要参数，对于这三个参数，本文采用以下方法求取。

①Hill法求取Kma。Hill法求取混合矿物有效模量是一种平均方法[7]，该方法求取混合矿物有效弹性模量的公式如式（4）和式（5）。

式中，kH为利用Hill法获得混合矿物体积模量；μH为利用Hill法获得混合矿物剪切模量；kV、kR分别为Voigt法[7]、Reuss法[7]获得的混合矿物体积模量；μV、μR分别为Voigt法[7]、Reuss法[7]获得的混合矿物剪切模量。

②Reuss法求取kf。1955年Wood[8]研究认为可以利用Reuss法[7]来计算孔隙中流体的体积模量kf。

孔隙中流体可能油、气、水单独存在，也可能多种流体共同存在，因此孔隙中流体的体积模量kf可用公式（6）表示。

式中，kw、ko、kg分别是水、油、气的体积模量；Sw、So、Sg分别是水、油、气所占孔隙体积的百分比。

③YMH法求取kdry。云美厚[9]在综合大庆油田和Phillips等人岩石物理实验以及大庆油田部分测井资料基础上，总结出干燥岩石体积模量和剪切模量与孔隙度、泥质含量、有效压力和温度之间经验关系，具体可用公式（7）表示。

式中，Md为干燥岩石的弹性模量，GPa；Pe为有效压力，MPa；T为温度，℃；Vsh为泥质含量；a0、a1、a2、a3、a4、b、c、d为拟合系数，各系数大小见表3。

表3 干燥岩石弹性模量拟合系数表

这里将利用云美厚求取kdry的方法称之为YMH法。

3.不同储层参数对纵波速度变化的影响

(1)储层参数

图1是依据储层钻井取样岩心测得2D、Upper B、Lower B三个储层孔隙度分布图，从图1中可看出2D储层的孔隙度主要介于[0.1,0.25]，Upper B、Lower B两个储层的孔隙度主要介于[0.1,0.3]。

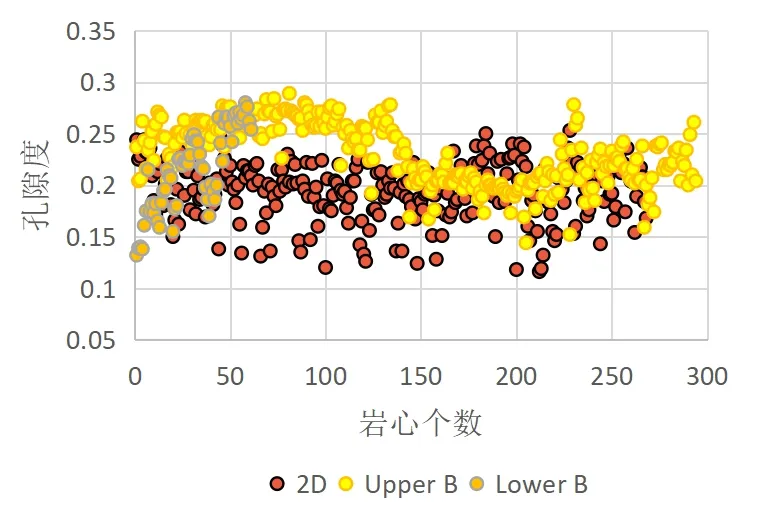
图1 不同储层岩心孔隙度分布图

2D储层的地面原油密度为0.84g/cm3，Upper B和Lower B两个储层的地面原油密度介于[0.84g/cm3，0.85g/cm3]。2D、Upper B、Lower B三个储层的温度都大致是75.5℃。2D的储层压力约是22MPa，Upper B、Lower B的储层压力约是22.3MPa。2D的围压约是45MPa，Upper B、Lower B的围压分别约是45.56MPa、46.2MPa。由已知数据，可知2D的有效压力约是23.0MPa，Upper B、Lower B的有效压力约是23.26MPa、23.9MPa。2D、Upper B、Lower B三个储层的泥质含量在储层不同位置存在差异，但不同储层位置的泥质含量范围变化介于[0,40%]。

2D、Upper B、Lower B三个储层基质组成矿物主要是石英和黏土，因此假设三个储层基质由石英和黏土矿物组成，表4提供了石英和黏土的弹性参数。

表4 石英和黏土的弹性参数[10]

由于Upper B、Lower B两个储层孔隙度范围相似、有效压力差异不到1MPa、储层温度一致、密度相近，因此对于Upper B和Lower B储层就不分别来进行研究，而是取平均储层参数来考察Upper B和Lower B地震波速度随不同储层参数变化，假设平均储层参数后的储层代号用B来表示。表5列出了2D储层和平均后的B储层地震波研究时涉及的储层参数，可看出B储层孔隙度范围包含了2D储层的孔隙度范围，两个储层的温度和泥质含量范围是一致的，两个储层的地面原油密度相差不大，差异仅为0.05g/cm3；两个储层的储层压力、围压和有效压力虽有差异，但不同压力差异都在1MPa以内。鉴于B储层包含了2D储层的孔隙度范围，且其它储层参数相差不大，因此这里只对B储层进行研究，其研究成果可为2D储层所借鉴。

表5 2D、B储层时移前的储层参数

(2)流体替换和储层压力改变对纵波速度变化的影响分析

目前S油田开采时主要发生流体替换和储层压力改变，其它储层参数不发生明显变化。由于B储层在不同深度存在不同孔隙度的砂岩，而不同孔隙度的砂岩又可能存在不同的泥质含量，参照孔隙度范围取0.1、0.2、0.3三种孔隙度来研究，对每种孔隙度又考虑0、0.2、0.4三种泥质含量情况。下面主要对流体替换和储层压力分别变化的情况开展分析。

①纵波速度随流体替换的影响分析。假设储层开采过程中只发生流体替换，图2展示发生流体替换时储层纵波速度随含水饱和度的变化关系图。图2中包括孔隙度为0.1、0.2、0.3三种情况，分别对应图2a、图2b、图2c，每种孔隙度又包括泥质含量分别是0、0.2、0.4三种情况。由图2可知，在一定孔隙度，相同含水饱和度变化情况下，纵波速度变化最大的是泥质含量为0.4的储层，其次是泥质含量为0.2的储层，再其次是泥质含量为0的储层，表6提供了B储层不同孔隙度砂岩中的油完全被水替换的速度差异，油被水完全替换时有时变化比较大，在孔隙度为0.3，泥质含量为0.4时，水替换油，纵波速度增大了345.57m/s，速度变化比例达到22.02%。

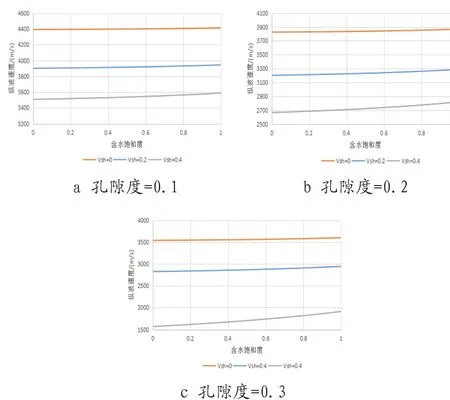
图2 B储层不同孔隙度砂岩中纵波速度随含水饱和度变化的关系图

表6 B储层不同孔隙度砂岩中的油完全被水替换的速度差异

②纵波速度随储层压力改变的影响分析。假设开采过程中只发生储层压力变化，且储层压力变化介于[15MPa,30MPa]研究发现在相同孔隙度情况下，随着储层压力的增大，纵波速度是减小，在孔隙度一定情况下，泥质含量越小，纵波速度的变化量越大。表7是不同孔隙度砂岩中储层压力从15MPa变换到30MPa的速度差异，由该表可以看出，在不同孔隙度情况下，泥质含量为0时，其速度变化量是最大的；在速度变化百分比方面，孔隙度为0.3，泥质含量为0.4的速度变化百分比相对其它略大一些，其它的都比较接近。

表7 B储层不同孔隙度砂岩中储层压力从15MPa变换到30MPa的速度差异

4.结论

通过以上地震波速度的研究，有以下三点结论。

（1）泥质含量对地震波速度变化产生影响，有时影响比较大，在高孔隙高泥质含量时，这一现象更明显；（2）油藏变化范围内对速度变化的影响，相对储层压力，流体替换对泥质含量更敏感一些。（3）相同孔隙度情况下，含泥质的砂岩储层比纯砂岩储层引起的地震波速度更大，对时移地震监测更为有利。