小半径曲线连续刚构转体桥双向称重与配重方案*

张付林,汪 东,王银辉,陈 闯

(1.宁波市轨道交通集团有限公司,浙江 宁波 315101; 2.中铁四局集团有限公司,安徽 合肥 230023; 3.浙大宁波理工学院土木建筑工程学院,浙江 宁波 315100)

0 引言

近年来,转体桥梁结构体系不断丰富,桥梁跨径和转体质量不断增大,不对称、变宽度、曲线桥梁等各种桥梁特点在转体施工中叠加,使得桥梁平转施工技术难度不断增大,也促进了平转施工技术的迅速发展[2-6]。无论何种桥梁,确保转体结构处于平衡状态是平转施工的关键,为此,转体结构的不平衡称重试验和配重是转体施工的关键技术之一,得到技术界广泛关注[5-8],并不断有新的技术探索和尝试[8-9],包括三维激光扫描技术的应用[10]。

当桥面线形为平曲线时,连续刚构桥受曲率影响,因施工误差导致的转动体顺桥向偏心的同时也会伴随横桥向偏心,形成双向不平衡[6]。曲线半径越小,跨径越大,这种偏离程度会越突出,所以,对于曲线半径较小、跨径较大(转体结构悬臂长)的桥梁,转体结构平衡称重更加需要关注。所以,转体施工前需对结构进行顺桥向和横桥向的平衡称重,在此称为“双向不平衡称重”。

宁波市轨道交通4号线跨越杭甬客运专线的曲线连续刚构桥,是一座曲率半径350m、转体结构单侧悬臂长度86m的大跨小半径曲线转体桥梁。本文以该工程为例,提出双向不平衡称重方案和配重方法,推导了相应的计算公式,可为类似桥梁转体施工提供参考和借鉴。

1 工程概况

1.1 工程简介

宁波市轨道交通4号线上跨既有杭深客运专线、萧甬铁路的节点桥,是一座转体施工的小曲率半径预应力混凝土连续刚构桥,桥面上行线路中心线曲率半径为350m,桥跨布置为(68+138+95)m,采用悬臂浇筑结合平转转体的施工方法。由于合龙位置需避开铁路线正上方,桥跨不对称布置,2个转体T构的悬臂长度分别为50m(27号墩T构)和86m(28号墩T构),主梁顶板宽11m、底板宽7m,27号墩T构梁高5～9m,28号墩T构梁高5～12m,均按1.8次抛物线变化,如图1所示。

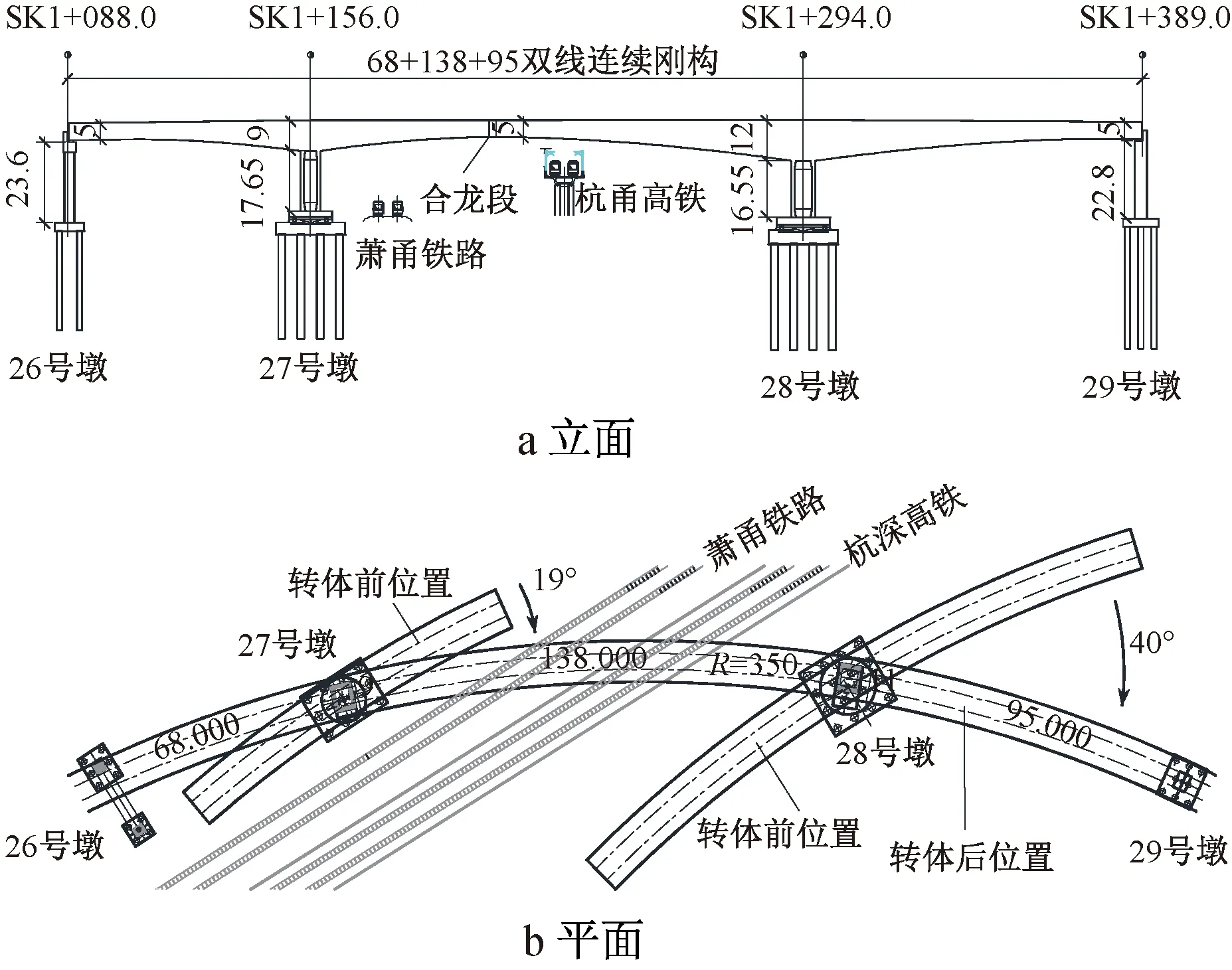
图1 桥型布置(单位:m)

图2 桥墩构造(单位:m)

受平曲率影响,转体T构重心偏离墩顶主梁截面中心线,为了确保转动铰中心与转体T构重心重合,转动铰中心向曲线内弧侧偏移0.8m(27号墩T构)和2.2m(28号墩T构),桥墩设计成曲线外侧直立、曲线内侧自梁底到承台顶倾斜的变截面墩身,如图 2所示。

27号墩T构转盘直径12.0m,球铰支撑半径1.5m,球铰的球心半径7.0m,滑道半径4.5m,滑道上方设8组撑脚,撑脚高度0.8m;28号墩T构转盘直径15.0m,球铰支撑半径2.0m,球铰的球心半径8m,滑道半径6.0m,滑道上方设8组撑脚,撑脚高度0.8m,如图3所示,撑脚设在转体结构顺桥向和横桥向轴线及转盘的1/8点(对角线)上。27,28号墩转体结构理论自重分别为81 626,156 013kN。

图3 转动铰构造示意(单位:m)

1.2 主要问题分析

由于平面曲率的影响,在箱梁悬臂浇筑过程中梁体重心可能产生双向累积误差,即梁体重心在顺桥向产生偏差的同时,也可能在横桥向产生偏差,从而形成有别于直线桥梁的双向偏心。平曲线曲率半径越小,横桥向偏心的可能性会越大。所以,曲线桥梁需进行双向不平衡称重,即进行顺桥向和横桥向2个方向的称重试验。

同样,顺桥向配重也会使横桥向产生偏心,所以根据称重结果进行双向配重时,同样需统筹考虑配重方案和效果。

依托项目曲线半径350m,转体结构最大悬臂长度达86m,相当于跨径175m的连续刚构桥梁的悬臂长度,为当前转体桥梁中梁长与半径之比最大的转体曲线桥梁。本文结合该项目的转体称重、配重过程详细介绍小半径曲线桥梁的双向不平衡称重和双向配重的方法。

2 双向不平衡称重原理

2.1 转体结构平衡状态分析

受曲率影响,曲线桥梁在顺桥向和横桥向均会因施工误差产生偏心,为获得双向偏心距以便确定配重方案,需对转动体进行顺桥向和横桥向2个方向的称重。目前转动体不平衡力矩计算应用最广的依然是球铰转动法[5-6],在上、下转盘间施加顶升力使得上、下球铰形成微小竖向转动(非平转,下文未注明均简称“刚体转动”),获得不平衡力矩及摩擦系数。由于球铰中心对称,可假定转体结构绕球铰中心发生任意方向刚体转动时,其最大静摩擦系数一致,即球铰最大静摩擦力矩MZ相同。

如图4所示,设转体结构顺桥向不平衡力矩为MGS,横桥向不平衡力矩为MGH,合力矩为MG。

图4 转动体系平衡状态分析示意

由图4可见,转体结构平衡状态可能出现以下几种实际情况:①转体结构不平衡合力矩MG小于球铰摩阻力矩MZ,此时,转体结构不会发生绕球铰任何方向刚体转动,无撑脚着地;②转体结构仅1个轴向不平衡力矩较大导致合力矩MG大于球铰最大摩阻力矩MZ,此时,转体结构一个方向上会发生绕球铰的刚体转动,一侧撑脚着地,另一个方向则无刚体转动,撑脚不着地,若图4中MGS较大而MGH较小,则转体结构发生顺桥向刚体转动,导致3号撑脚着地;③转体结构2个方向的不平衡力矩均较大导致合力矩大于球铰最大摩阻力矩MZ,此时,转体结构在对角线方向发生绕球铰的刚体转动,则可能对角线上撑脚乃至2个撑脚着地,如图4中出现2号撑脚着地,且可能伴随1号或3号撑脚同时着地。对平衡状态的预判是进行双向称重试验的基础。

2.2 不平衡合力矩小于球铰摩阻力矩

当解除转体结构临时锁定后,若双向均不发生绕球铰的刚体转动,所有撑脚均未着地,则可判断转体结构球铰摩阻力矩大于不平衡合力矩。

首先选择一个方向进行称重试验。假定选择顺桥向,分别在左、右两侧顶升上转盘,如图4所示,并记录顶升力-位移曲线。分别记录转体的位移曲线突变时的顶升力P1S和P2S,与常规称重方法一样,分别通过平衡方程得到顺桥向不平衡力矩MGS和摩阻力矩MZ:

(1)

(2)

然后在另一方向(横桥向)进行称重试验。选择其中一侧(图4中1号撑脚位置)顶升上转盘,同时记录顶升力-位移曲线。记录转体的位移曲线发生明显突变的顶升力P1H,则可得到横桥向不平衡力矩MGH:

MGH=MZ-P1H·L1H

(3)

可见,由于任意方向刚体转动时摩阻力矩相等,MZ已由前一次称重试验的式(2)得到,所以该方向的称重无须2侧分别顶升。

2.3 不平衡合力矩大于球铰摩阻力矩

当解除球铰的临时锁定后,若转体结构发生绕球铰的刚体转动,有撑脚着地,则可判断转体结构不平衡合力矩大于球铰摩阻力矩。此时,可能存在2种情况,即不平衡状态②和③。这2种情况的双向不平衡称重方式和计算方法基本一致。

假设在不平衡合力矩作用下,图4所示转体结构的对角线上2号撑脚着地,且3号撑脚伴随着地,则可判断MGS影响更大,所以可选择在3号撑脚位置先顶升,当转体结构发生微小刚体转动时,顶升力-位移曲线出现突变,记录顶升力P2S,然后千斤顶卸载,通过顶升力-位移曲线判断转体结构发生反向刚体转动时的顶升力为P′2S, 与常规称重方法一样,根据这2个时刻的平衡方程,可得到不平衡力矩MGS和摩阻力矩MZ:

(4)

(5)

然后在另一方向(横桥向)进行称重试验。采用与2.2节相同步骤,在1号撑脚顶升,得到与式(3)相同的横桥向不平衡力矩MGH。

如果仅3号撑脚落地,可采取前面相同的方法,如果仅2号撑脚落地,则第1次称重可选择顺桥向(3号撑脚位置顶升),也可选择横桥向(2号撑脚位置顶升),但在称重前作可能的不平衡力矩方向判断非常重要(见3.1节)。同时,需要注意的是,当一个方向顶升时,需对另一个方向需做好保护。

2.4 偏心距

根据上述计算结果,可得到顺桥向和横桥向偏心距eS,eH:

(6)

(7)

式中:G为转体结构自重。

转体结构合偏心距e:

(8)

由于转体结构的合偏心距大于2个方向的偏心距,所以,在曲线桥梁转体结构偏心距控制时,应以合偏心距为控制目标。

静摩擦系数μ[6,8]计算如下:

(9)

式中:R为球铰球面半径;μ为球铰静摩擦系数。

3 称重及配重

3.1 平衡状态判别

在转体结构的临时锁定解除前,在顺桥向、横桥向4个撑脚处(即图4中的1,3,5,7号)撑脚旁布置位移传感器;在逐步解除临时支撑过程中连续测量读数,观察撑脚随临时锁定拆除的位移,判断转体结构的平衡状态及可能的不平衡力矩方向。

3.2 称重结果

3.2.127号墩转体结构不平衡称重试验

1)27号墩转体结构在临时约束解除完毕后跨中侧撑脚着地,属于情况②的平衡状态,因此先进行顺桥向不平衡称重,其顶升力-位移曲线如图5a所示。

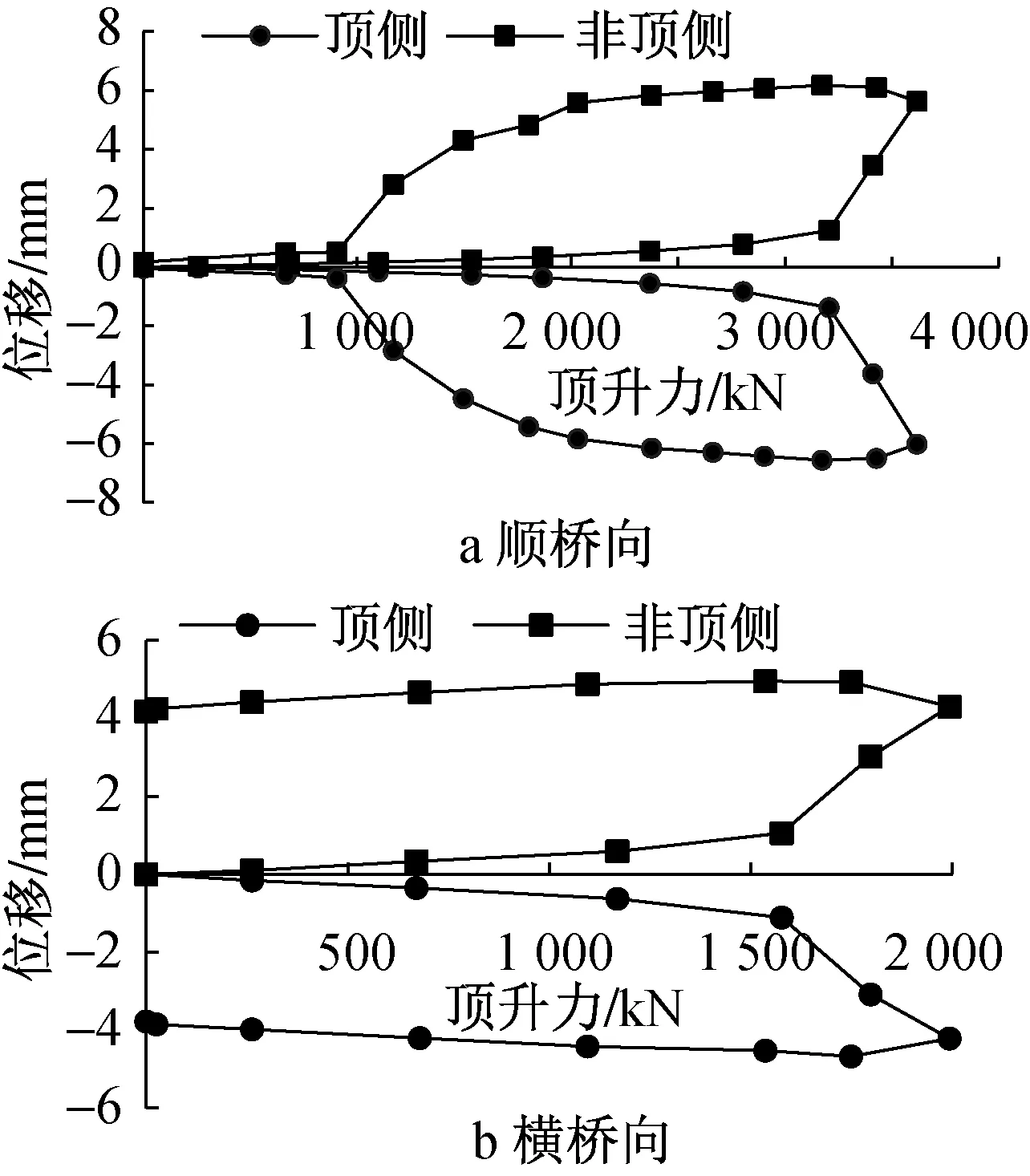
图5 27号墩转动体称重顶升力-位移曲线

由图5a可见,P2S=3 205kN,P′2S=1 496kN。 转动体理论自重G为81 626kN,L2S=4.5m,根据式(4)、式(5)可得:MGS=10 577kN·m(跨中侧),MZ=3 845kN·m。 由此得到转体结构纵向偏心距eS为13.0cm(跨中侧),静摩擦系数μ=0.006 9。

2)进行横桥向称重,由于横桥向撑脚未落地,选择一侧起顶(根据临时解锁过程中观察转体结构在曲线内侧有下沉位移,故选择该侧起顶),其顶升力-位移曲线如图5b所示。

由图5b可见,球铰竖向转动临界力P1H= 1 576kN, 由式(3)可得横向不平衡力矩MGH=3 247kN·m (曲线内侧),得到转体结构横向偏心距eH为4.0cm(偏向曲线内侧)。

由式(8)得到合偏心距e为13.6cm。

3.2.228号墩转体结构不平衡称重试验

1)28号墩转体结构在临时约束解除完毕后,出现2个撑脚同时着地,分别为横桥向曲线外侧撑脚,及与跨中侧之间的对角线位置撑脚,属于情况③的平衡状态,可判断偏心距横桥向向曲线外侧偏离,顺桥向向跨中侧偏离。故先进行横向称重试验,曲线外侧撑脚位置顶起,顶升力与位移曲线如图6a所示。

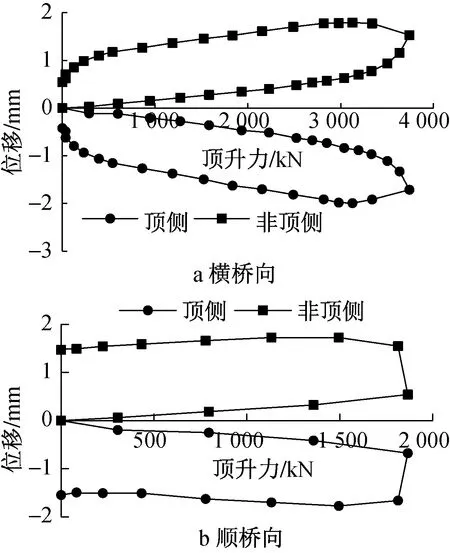
图6 28号墩转动体称重顶升力-位移曲线

由图6a可见,P2H=3 504kN,P′2H=232kN。转动体理论自重G为156 013kN,由L2H=6m,式(4)、式(5)可得:MGH=11 207kN·m(曲线外侧),MZ= 9 817kN·m。 转体结构横向偏心距eH为7.2cm,静摩擦系数μ=0.008。

2)进行顺桥向称重,根据撑脚情况可判断转体结构偏向跨中侧,故在跨中侧顶起,其顶升力-位移曲线如图6b所示。

由图6b可见,球铰竖向转动临界力P1S=1 866kN, 求得纵向不平衡力矩MGS=1 379kN·m(跨中侧),纵向偏心距eS为0.8cm(偏向跨中侧),可见顺桥向偏心距很小。计算得合偏心距e为7.2cm。

3.3 配重

3.3.1配重分析

本工程分别确立悬臂浇筑倒数第2节段区域和桥墩曲线外侧(设置挂配重位置)3个位置作为配重区。显然,悬臂端配重会产生横桥向偏心距,而桥墩外侧配重则不会影响顺桥向偏心距。通过有限元分析,得到单侧悬臂端配重区域施加配重时,配重与顺桥向、横桥向偏心距关系如表1所示,桥墩外侧配重对横向偏心距的影响如表2所示。

表1 单侧施加配重对偏心距的影响

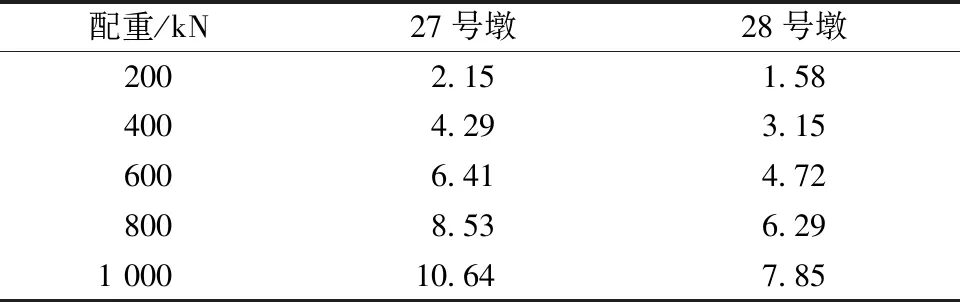
表2 墩外侧配重对横向偏心距的影响

根据配重分析,悬臂端区域配重对横向偏心的影响不可忽略,而墩外侧配重对横向偏心的调节效果则不敏感。所以,曲线桥梁转体结构配重建议遵循“先顺桥向后横桥向”原则。此外,横向配重还应考虑转动体的横向受力变形。

3.3.2配重

考虑到部分撑脚着地可使得转体结构在平转时更加平稳,但撑脚支撑力过大也会过多增加平转时的摩擦力矩,从而过多增加牵引力。所以,应通过配重达到有撑脚着地,且支撑力较小是一种较佳的配重结果,也就是配重需控制配重后不平衡合力矩M′G略大于MZ。

对于27号墩转体结构,根据称重结果,由MZ和转动体自重G(配重自重影响远小于G,可忽略)可得到:当e>MZ/G=4.7cm时,达到撑脚着地状态。由于横向偏心距eH为4.0cm(偏向曲线内侧),则确定通过配重使得纵向偏心距eS为3.0cm(跨中侧)时,合偏心距为5.0cm,满足要求。由此,根据表1结果内插得到需边跨侧悬臂端配重185kN。同时,该配重同样会导致横桥向向曲线内侧偏心增大0.45cm。所以配重后实际纵向偏心距eS为3.0cm(跨中侧),横向偏心距eH为4.5cm(偏向曲线内侧),合偏心距为5.4cm。实际施工中,按此方案配重后,对角线上撑脚着地,但支撑力较小,对牵引力影响小,且可保证平稳转体,是一种理想的转体平衡状态。

对于28号墩转体结构,根据称重结果,由MZ和转动体自重G可得到:当e>MZ/G=6.3cm时,达到撑脚着地状态。而根据称重结果,纵向偏心距eS为0.8cm(偏向跨中侧),横向偏心距eH为7.2cm(偏向曲线外侧),合偏心距e为7.2cm,略大于控制值6.3cm,可见该状态能较好地满足撑脚着地且撑脚支撑力较小的控制标准,故不再需配重。

为更好地控制转体牵引力,可按配重后平衡状态计算撑脚支撑力,通过支撑力引起的摩阻力矩计算转体牵引力,本文限于篇幅不再赘述。

上述称重试验与配重方案有效保证了本工程转体施工的平稳顺畅。

4 结语

1)转体结构临时锁定解除过程中应观测转体结构位移,初步判断不平衡状态,为设计双向不平衡称重试验方案提供依据。

2)由于球铰的中心对称特点,可假定转体结构任意方向刚体转动静摩擦系数一致,可减少顶升次数,提高称重试验效率。

3)配重对调节顺桥向偏心敏感,而对横桥向偏心不敏感,在配重方案设计时,宜采用“先顺后横”配重策略,同时以合偏心距控制为目标,调节时以顺桥向偏心距为主、横桥向偏心距为辅,并充分考虑曲率影响下顺桥向配重对横桥向偏心的影响。

4)以配重后不平衡合力矩略大于摩阻力矩为合偏心距控制目标,既能使撑脚着地以提高转体结构稳定性,又可控制撑脚较小的支撑力,从而控制转动牵引力,同时还能减少配重量。