基于浸入与不变自适应的机械臂轨迹跟踪控制方法

汤元会,张 璐

(陕西省计量科学研究院 电子与电磁计量研究所,陕西 西安 710100)

0 引 言

随着制造业的不断发展,机械臂作为一种高性能自动化设备,已广泛应用于生产工业的各个领域[1-2]。然而,机械臂系统具有非线性、强耦合、多变量等特点,易受到模型参数变化的影响[3],对机械臂轨迹跟踪控制带来困难。而在一些高精度应用领域,机械臂须具备更高的精确性和更稳的控制性能。因此,如何提高机械臂在模型不确定情况下的跟踪性能具有重要意义。

在实际应用过程中,很难对机械臂建立精确的动力学模型,模型中往往存在不确定参数。自适应控制因其具有强大的自学能力和鲁棒性而得到广泛的研究[4]。文献[5]针对模型不确定机械臂的轨迹跟踪问题,通过神经网络的逼近能力能够补偿非线性系统的不确定性,设计了基于自适应神经网络的输出反馈控制方法。文献[6]提出了一种自适应模糊反步控制器,以解决机械臂系统中存在的各种非线性和不确定性的问题。文献[7]将干扰观测器和自适应滑模控制方法相结合,解决了建模误差和各类干扰带来的不确定性。以上方法对具有模型不确定性的机械臂轨迹跟踪控制问题有一定的贡献,且都是基于确定性等价原则(certainty equivalence, CE)对不确定参数进行辨识[8]。基于CE设计的参数自适应律,并不是真正估计未知参数值,而是为了消除Lyapunov函数导数中存在的不确定参数项的影响,因此在参数自适应律中并不含有参数估计误差的负反馈项,而是和跟踪误差直接耦合在一起,这就导致跟踪误差影响参数估计的过程,而参数估计在控制器中影响跟踪误差的动态,两者直接耦合造成系统闭环性能下降,参数估计误差和跟踪误差无法同时收敛到0,且会出现过参数化问题[9]。虽然文献[10]解决了这一问题,但是取而代之的是一个更复杂的参数自适应律[11]。

为实现优化,文献[12]提出了基于非确定性等价(Non-Certainty Equivalence,NonCE)原则的浸入与不变(Immersion and Invariance,I&I)理论。该理论是将一个关于状态的修正项引入到参数估计误差中,即在参数估计误差的微分项中增加不确定参数,确保参数估计误差能够收敛到零。但是修正项需求解一个偏微分方程(Partial Differential Equation, PDE)。对一阶系统,偏微分方程的解可以通过积分求取;对高阶系统,偏微分方程不一定存在解析解,这一情况被称为“可积性障碍(Interability Obstacle)”。

针对这一障碍,文献[13-15]提出将动态缩放技术(Dynamic scaling)应用到I&I自适应方法中。该方法在求解过程中引入状态滤波器,将回归矩阵中的部分状态变量替换成滤波器的估计值,使待求解的偏微分方程可解并积分得到其近似解,再引入动态缩放因子消除了近似解和实际解之间的误差。目前该方法的相关应用多体现在飞行器控制系统上[16-20],而在同样具有强耦合、非线性特性的机械臂系统上却鲜有研究。

本文针对具有惯性矩阵参数不确定性的机械臂动力学模型,提出了一种基于改进I&I自适应方法的轨迹跟踪控制方法。首先,针对I&I自适应理论在机械臂动力学模型中存在“可积性障碍”的问题,引入状态滤波器,构造新的参数回归矩阵求得PDE的近似解,并通过设计动态缩放因子消除矩阵改造前后的误差对系统性能的影响。仿真结果表明,本文所提出的方法具有更优异的跟踪精度和动态特性。

1 机械臂系统模型

以双关节机械臂模型为研究对象,其结构示意图如图1所示。

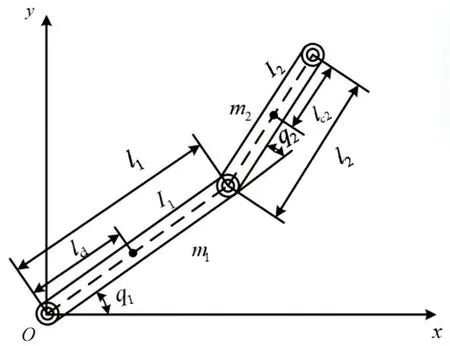
图1 双关节机械臂示意图Fig.1 Schematic diagram of a two-joint manipulator

图1中,li(i=1,2)为连杆长度;qi(i=1,2)为关节转动角度;mi(i=1,2)为连杆质量;lci(i=1,2)为连杆到质心的距离;Ii(i=1,2)为惯性矩阵。其动力学方程可表示为

在实际运行过程中,惯性矩阵M会发生摄动而使其具有不确定性,因此将惯性矩阵的逆矩阵M-1视为不确定参数。

为提高机械臂跟踪精度,选取惯性矩阵为未知参数变量,并设计I&I自适应参数估计器和系统的非线性控制律,以确保机械臂关节轨迹能够跟踪期望轨迹。

2 自适应控制器设计

2.1 I&I自适应参数估计器设计

为了便于后续对I&I自适应参数估计器的设计,将式(2)所表达的含有不确定参数的双关节机械臂动力学模型整理为

式中：θ=[θ1θ2θ3],为经过数学变换后的未知惯性矩阵;

ΦT(x1,x2,x3)=[Φ1(x1,x2)Φ2(x1,x2)]=

针对式(3)所表示的非线性系统,设计I&I自适应参数估计器,使其能对未知参数θ值进行估计。I&I自适应参数估计器的构造可以分为3步。

Step 1：根据文献[8],定义不确定参数的估计误差,按照I&I自适应控制理论,设计修正项函数β(x)。原则上,β(x)的设计需要求解偏微方程(PDE),但这对于大多数多变量系统来说非常困难。

定义参数估计误差为

式中：k(·)为待设计的矩阵。

对式(4)求导,得到参数估计误差的动态方程为

本文所设计的参数自适应律为

将式(7)代入式(6)中得到

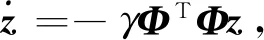
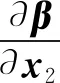
(9)

式(9)所示的PDE不满足可积条件,无法求得该式的解析解。因此下一步通过“近似解”的方法来求解偏微分方程(9)。

Step 2：根据文献[13]的PDE“近似解”的方法：引入状态滤波器,将回归矩阵Φ(x1,x2)中的积分变量用滤波器输出替代,通过积分得到近似解。本文所设计函数β的具体表达式为

式中：γ>0。

式中：函数δij(·)∈R2。

将式(10)和式(11)代入式(8),得到参数估计误差的动态为

-γΦT(x1,x2)Φ(x1,x2)z+

式中：Δj(x1,x2,ex2)=[δ1j(x1,x2,ex2)δ2j(x1,x2,ex2)]。从式(12)很明显看出,Δj(·)是由状态滤波器引入的误差项,也可以将其视为偏微分方程真解和近似解之间的误差。接下来引入动态缩放因子[14]消除偏微分方程真解和近似解之间的误差。

Step 3：引入动态缩放因子[14],消除近似解和真解之间的误差,降低前面干扰项的影响,并加快系统的收敛速度,同时也证明所设计的I&I自适应参数估计器的参数估计误差收敛到零。引入动态缩放因子r,定义缩放后的参数估计误差：

式中：r是待设计的动态缩放因子。对式(13)求导并将式(12)代入得到：

所设计的动态缩放因子的具体形式为

对滤波误差ex2求导,并将式(3)和式(5)代入,得到滤波误差的动态方程为

式中：k(·)为待设计的对称矩阵。

通过设计矩阵k(·),确保动态缩放因子r是有界的,并且系统在(η,ex2)=(0,0)处具有全局一致稳定的平衡点,即

k=κr2I+εcr2diag‖Δj(x1,x2,ex2)‖2

(17)

式中：κ和ε为正常数。

构造Lyapunov函数V(η)=0.5ηTη,对其求导并将式(14)代入,并结合Yang不等式得

因此,系统在原点具有全局一致稳定的平衡点,且从式(13)和上述分析明显看出,如果r∈L∞,则z(t)→0。下面验证r的有界性。

首先构造Lyapunov函数

对式(19)求导并将式(16)、(17)、(18)代入,结合Yang不等式得到

由此得到系统在(η,ex2)=(0,0)处具有一致全局稳定的平衡点。

构造Lyapunov函数

对其求导,并将式(14)、(15)、(16)、(17)代入得

2.2 反步控制律设计

基于反步控制方法设计机械臂的控制输入τ,其具体设计过程如下。

Step 1：定义跟踪误差e1=x1-xd,对其求导得

定义x2的跟踪误差信号：

e2=x2-α1

(25)

式中：α1为x2的虚拟控制输入,设计虚拟控制律α1使e1稳定。结合Lyapunov稳定性定理,将虚拟控制律α1设计为

式中：c1>0。

将式(25)、(26)代入式(24)得

Step 2：对式(25)所定义的误差信号求导得

式(29)中,出现了系统的真实控制输入τ,基于Lyapunov稳定性定理,本文设计的最终控制律为

Cx2+G

(30)

式中：c2>0。将式(30)代入式(29)可得

3 仿真结果及分析

为验证本文所设计控制器的有效性,在机械臂系统参数和控制器参数保持一致的情况下,选取双关节机械臂动力学模型作为仿真对象,通过Matlab/Simulink软件进行仿真,对2种控制方法进行比较。方法1是本文所设计的基于I&I的参数不确定机械臂自适应轨迹跟踪控制方法(IABC,Immersion and Invariance based Adaptive Backstepping Control);方法2是模型参数已知的反步控制方法(FPBC,Fixed Parameter Backstepping Control)。

双关节机械臂系统参数选择如下：

其中

m1=2 kg,m2=0.8 kg,l1=0.5 m,l2=0.5 m,lc1=0.25 m,lc2=0.25 m,g=9.8 m/s2,不确定参数的真实取值为θ=[5 2,2 3]。反步控制器增益采用试凑法,最终取值为c1=1.5,c2=20。跟踪的期望轨迹设计为xd=[sintsint]T。机械臂关节位置的初始值设置为x1=[0 0]T,机械臂关节速度的初始值设置为x2=[0 0]T。自适应估计器的参数设置为c=γ=10,κ=λ=0.1,ε=0.1,动态缩放因子的初始值设置为r(0)=1。

机械臂系统轨迹跟踪控制的目标是令机械臂关节角追踪误差迅速收敛,并且机械臂的关节角度能对期望轨迹实现准确快速的跟踪。图2分别是2个关节的轨迹跟踪响应曲线。可以看出： 在所提IABC的作用下,无论是关节1还是关节2的轨迹跟踪响应曲线,都在短暂的动态之后跟踪上期望轨迹,系统很快进入稳定状态。因系统参数的不确定性对控制精度带来的影响被I&I自适应估计器有效抑制,在IABC方法下机械臂的关节能够很好地跟踪期望轨迹,拥有良好的跟踪性能。在相同的控制参数的情况下,使用FPBC的系统一直存在周期性的跟踪误差,本文所提出的IABC方法在跟踪性能上明显优于FPBC。

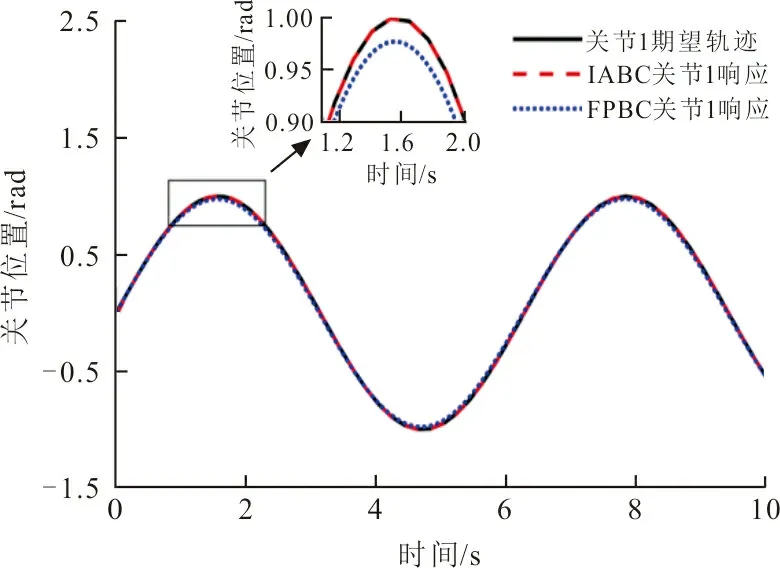
(a) 关节1轨迹跟踪响应曲线

图3是IABC和FPBC算法下双关节刚性机械臂的轨迹跟踪误差曲线。

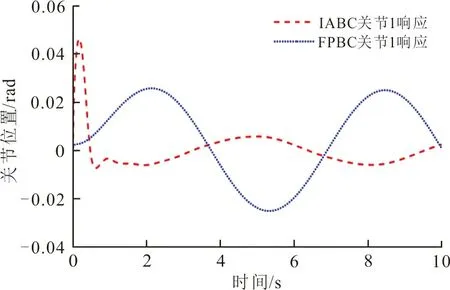
(a) 关节1轨迹跟踪误差

从图3(a)可以看出：关节1在FPBC方法下始终未能跟踪上期望轨迹,0～10 s内的误差一直在±0.025 rad之间,并且呈现周期性的变化。虽然开始时误差较小。但是始终存在误差,系统的跟踪性能不够优越。而本文所提IABC方法虽然在开始时的跟踪误差在0.046 rad左右,但是在0.7 s后,跟踪误差始终保持在±0.006 rad之间,最大稳态误差相比FPBC方法降低了约76%,误差变量收敛范围更小,跟踪效果更优。

从图3(b)可以看出：FPBC方法下的关节2在0～10 s内的跟踪误差一直保持在±0.023 rad之间,始终存在周期性的误差。IABC方法在开始时最大跟踪误差达到0.016 rad左右,但是约在0.3 s后实现对给定轨迹的精确跟踪,最大稳态误差相比FPBC方法降低了约99.6%,跟踪效果明显优于FPBC方法。

图4分别是状态滤波器的响应曲线。从图4中可以看出：2条曲线基本重合,说明可以利用状态滤波器估计值求解偏微分方程。但是2条曲线并没有完全重合,存在估计误差,因此偏微分方程的解只是近似解,与真值解之间存在一定的误差。

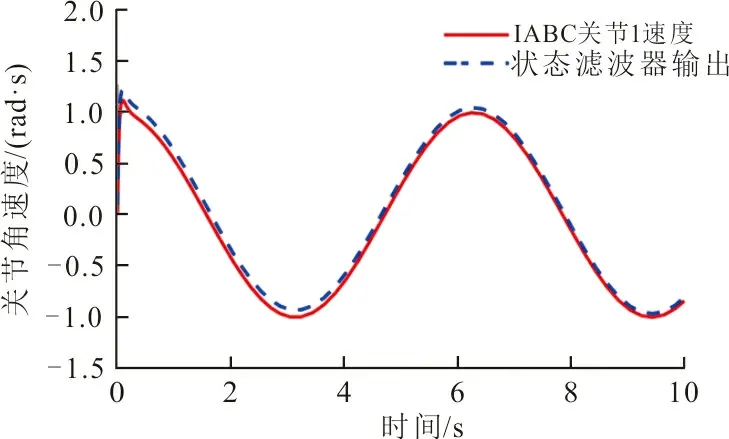
(a) 关节1速度的滤波值

图5为所设计的动态缩放因子r的响应曲线。观察图5可知,动态缩放因子在系统运行一段时间后保持平稳,验证了文中对动态缩放因子r有界的证明。

图5 动态缩放因子响应曲线Fig.5 Response curve of dynamic scaling factor

和β1响应曲线

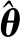
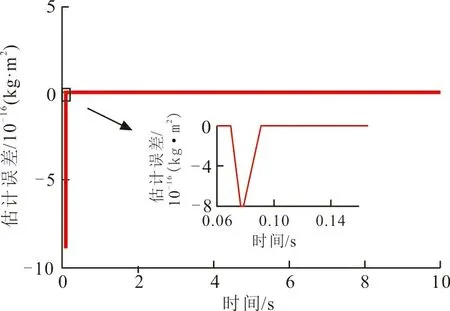
(a) 参数估计误差z1的响应曲线

4 结 语

为解决双关节机械臂在运动过程中的系统稳定性和跟踪精度的问题,提出一种基于I&I自适应反步控制方法。增加了含有状态变量的非线性可调节函数,提高了参数估计器的灵活可控性。同时,在I&I自适应参数估计器中引入状态滤波器,求出偏微分方程近似解,然后通过引入动态缩放因子消除近似解和真实解之间的误差。本文所提控制方法避免了过参数化问题,在保证控制系统对参数自适应能力的同时,降低了机械臂系统的跟踪误差,有效提高了系统的跟踪性能。