改进自抗扰下的细纱机卷绕系统控制策略
廉继红,王炳炎,王延年,王 栋
(西安工程大学 电子信息学院,陕西 西安 710048)
0 引 言
细纱是纺纱过程的重要工序,它将粗纱纺制成细纱并卷绕于筒管之上制成管纱。卷绕过程的好坏对管纱质量和成品率有着非常重要的影响[1]。由于在卷绕细纱的过程中,纱线上的张力是不断变化的,永磁同步电机需要随着卷绕过程的进行不断调速,而调速过程中,永磁同步电机的转速、转矩就会产生剧烈波动,此时极易出现纱线断头的现象[2]。而永磁同步电机先进控制策略被越来越多地用来解决以上问题[3-4]。
近年来,国内外学者提出了许多先进的控制策略,常见的有广义预测PID控制算法与滑模自抗扰控制算法[5-6]。广义预测PID控制算法中,利用广义预测算法对PID参数进行整定,但预测精度不高,存在误差较大。传统的滑模自抗扰控制算法中,扩张状态观测器的初始峰值问题没有得到解决,且滑模控制存在一个不可避免的问题,即在系统运行至滑模面后,无法严密沿着滑模面朝稳定点的方向运动,从而形成高频抖振。
为此,本文提出了改进GWO算法下的基于增益可调扩张状态观测器与改进型趋近率滑模控制联合改进的自抗扰控制策略。首先采用基于增益可调扩张状态观测器的改进自抗扰控制方法,降低了传统扩张状态观测器中的初始峰值,提高了观测精度[7]。其次利用改进型趋近率滑模控制代替自抗扰中的状态误差反馈控制器,由于可变参数较多,同时采用改进GWO算法对控制参数进行调节,提高了参数的精确度,不仅提高了滑模控制器的收敛速度,也降低了高频抖振。最后通过仿真验证表明本文提出的控制策略驱动永磁同步电机,能有效提高电机调速性能,提高管纱质量,且能降低系统的波动,防止细纱断头。
1 系统建模
细纱卷绕是将成品细纱制成管纱的关键步骤,卷绕系统的关键部分是带动筒管转动的永磁同步电机。以下对卷绕系统和永磁同步电机进行建模。
1.1 细纱机卷绕系统建模
从图1可以看出,粗纱经过导纱杆从粗纱管上退绕下来,立刻被导纱杆导入横动装置,经横动装置喂给纱线到牵伸装置,牵伸装置会将喂入的须条均匀牵伸,使得纱线达到所需要的特数。牵伸完成后由导纱钩牵引纱线到钢领板上进行加捻[8],最后将加捻后的纱线进行卷绕,使纱线成型规律、紧密一致地卷绕在纱筒上,便于后续加工使用。

图1 细纱机卷绕系统原理Fig.1 Schematic of spinning frame winding system

图2 常规趋近率性能Fig.2 Conventional approaching rate
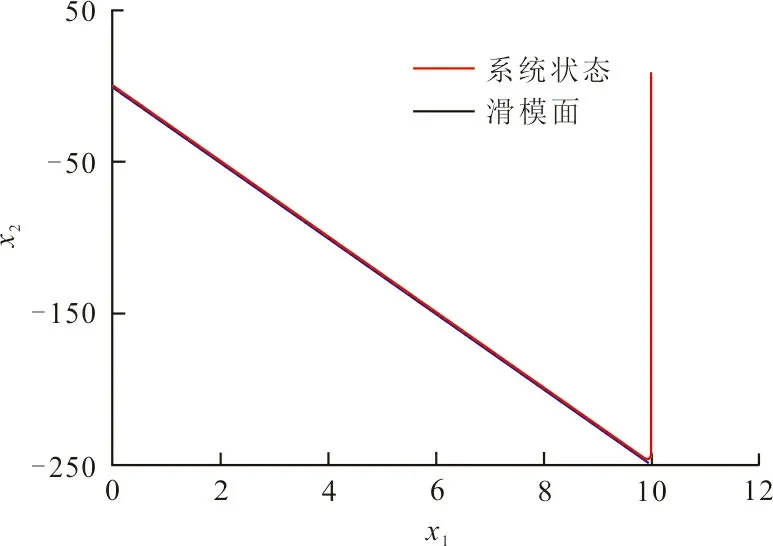
图3 改进趋近率性能Fig.3 Improved approaching rate ability
在细纱卷绕过程中,永磁同步电机用来控制纱锭的运动,根据卷绕系统模型和卷纱几何规律可知:
式中:v为纱线卷绕线速度;vr为往复导纱速度;h为法相螺距;rk为纱筒的卷绕半径。
卷绕半径rk可表示为
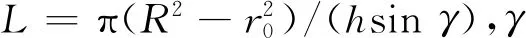
由式(2)可得,导纱机构运动速度可表示为
1.2 永磁同步电机的数学模型
永磁同步电机是一种复杂的非线性系统,内部转子和三相绕组之间相互作用存在耦合,为了便于分析各个参数之间关系,假设:
1) 内部铁芯不存在饱和的情况;
2) 不需要考虑电机内部涡流的损耗;
3) 转子和永磁体无阻尼。
永磁同步电机三相静止坐标系abc下的电压方程为
式中:ua、ub、uc为三相电压;ia、ib、ic为三相电流;Rs为转子电阻;φa、φb、φc为三相磁链。
为了简化计算,将三相静止坐标系abc转化为两相dq坐标系[9],则电压方程为
式中:id和iq为定子电流;ud和uq为定子电压;Ld和Lq为定子电感;φf为永磁体磁链;R为定子电阻;ωe为转子角速度。则永磁同步电机运动方程为
式中:B为黏滞摩擦系数;p为极对数;J为转动惯量;ω为实际机械角速度;TL为负载转矩。最终得到永磁同步电机转矩方程为
2 永磁同步电机改进自抗扰控制器
2.1 自抗扰控制系统设计
自抗扰控制是一种无模型且鲁棒性强的非线性控制方法,因其灵活性高被广泛应用于工业控制中。自抗扰控制器由跟踪微分器、扩张状态观测器及状态误差反馈控制器组成[10]。其中,跟踪微分器的作用就是将输入进来的信号经过处理,输出2类信号;扩张状态观测器将影响输出的扰动扩张为新的状态观测变量,准确地观测扩张后的总扰动量,并对其进行自动补偿;状态误差反馈控制器则是将跟踪微分器的过渡量和扩张状态观测器的状态估计量两者的偏差进行组合,并对整个控制系统作出有效补偿[11-12]。
由于永磁同步电机速度控制是一阶的,不需要二阶变量,为了简化设计,舍弃跟踪微分器。
在扩张状态观测器中,fal是一个非线性函数,用于消除系统扩张了一个状态后产生的未知函数对系统的影响,表达式为
式中:e为输入误差变量;α为非线性系数且0<α<1,δ为滤波系数。
扩张状态观测器在设计过程中,仅设计合适的增益系数就可以实现对系统总扰动精准观测[13-14]。但传统fal函数是不连续函数,此函数在不连续点的切换会使得动态增益出现波动,容易出现观测量抖振的问题。因此提出增益可调扩张状态观测器对系统的扰动进行观测[15-16]。
首先定义一个具有连续可导特性的误差矫正函数:
式中:λ为误差增益。本文选取α=0.5,λ=5 000,由于传统扩张状态观测器在增益参数较大时,会导致扩张状态观测器的初始状态z1与系统的初始状态ω之间的误差较大,且估计值z2对总扰动f的跟踪不准确,容易产生峰值问题。因此,本文提出的可调增益状态观测器[17-18]可表示为
式中:β1、β2是误差矫正因子;r(t)为变增益;b0为补偿因子;e1为初始状态误差。状态误差反馈控制器可设计为
式中:e2为输出状态误差;ω*为期望角速度;β3为误差矫正因子。
2.2 滑模自抗扰控制系统设计
上述方法解决了传统扩张状态观测器中的峰值问题。速度误差经过状态误差反馈控制器的输出精度略微提高,但该控制器应用于纱线卷绕系统中鲁棒性有待提高。
滑模控制具有响应速度快、鲁棒性强、可靠性高等特点[19],但是在系统达到稳态时会有抖振的产生,而自抗扰控制方法中的扩张状态观测器能够有效的观测系统受到的不确定扰动,并在反馈中对系统的扰动值进行补偿。滑模控制中存在的抖振问题可以利用自抗扰控制中的扩张状态观测器进行消除[20-21],因此,本文提出用改进滑模控制代替状态误差反馈控制环节,设计自抗扰控制与滑模控制相结合的改进型趋近律的滑模自抗扰控制器。
本文利用积分型滑模面表达式如下:
式中:c为大于零的变量;e0为跟踪误差,e0=ω*-ω。为了提高趋近阶段的动态质量,本文使用改进型趋近率:
式中:σ、K、η为增益系数。以常规单变量系统对改进型趋近率进行验证,状态方程为
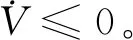
取滑模面S=ZX0,可得控制函数:
通过观察2种趋近律的相轨迹仿真结果可以看出,改进型趋近率在单变量系统中能收敛到平衡点,并且能比传统指数趋近律以更快的速度趋近到滑模面。
sgn(S)S-KS2-(f-z2)S
(16)
2.3 基于GWO算法的改进滑模自抗扰控制
上述方法不仅解决了传统扩张状态观测器中的峰值问题,也有效地克制了滑模控制结构中的抖振问题。但是在滑模自抗扰控制方案中,滑模控制部分可变参数较多,这些参数需要按照经验给定,因此就需要较长的时间才能调整出合适的参数[22],为了提高参数的精度,同时提高效率,本文采用GWO算法对需要整定的参数进行寻优。
GWO算法是一种新兴的启发式优化算法,其基本思想是模拟灰狼群体的社会行为[23],实现全局优化。
对灰狼行为建立数学模型[24]:
式中:Xp(t)为目标状态;X(t)为灰狼坐标;D为灰狼与目标之间的长度;X(t+1)为灰狼根据目标状态进行下一次围堵的目标位置;A和C为控制系数A=2a·r1-a,C=2r2,其中,r1和r2为大于0小于1的变量,a为非线性收敛因子。
为提高算法的优化性能,并避免寻优期间陷入局部最优,本文采用的非线性收敛因子a可表示为
式中:e为自然指数;t为迭代次数;tmax为最大迭代次数。
适应度函数可表示为
式中:n为采样总数。当灰狼搜索到猎物位置后,头狼会带领次头狼和执行狼指导其他狼群进行捕猎,利用头狼最靠近猎物的优势,来通过这头狼判断猎物位置,从而逐渐逼近猎物,确定灰狼个体的移动方向,不断更新位置信息,最终确定猎物定位,完成捕猎过程。GWO算法优化控制系统步骤如下:
1) 初始化,令时间为0,迭代次数t=0,最大迭代次数tmax,种群数N;
2) 运行程序得到改进自抗扰控制参数,计算出永磁同步电机模型;
3) 计算适应度函数,运行系统模型,记录当前最优解;
4) 筛选最优参数,循环次数N=N+1;
5) 迭代次数达到tmax停止迭代,输出最优解。
3 实验结果分析及讨论
3.1 实验平台搭建
利用Simulink搭建永磁同步电机控制系统,设定电机初始参数如下:
直流母线电压311 V,电机转速18 000 r/min,额定电流40.4 A,转子磁链0.186 6 Wb,极对数4对,交流电感0.964 4 mH,直流电感0.756 6 mH。
3.2 实验分析
电机在卷绕细纱的过程中,随着管纱上纱线从小纱到大纱的转变,对应的卷绕速度也要做出相应的改变。电机在设定转速为18 000 r/min,带负载TL为50 mN·m时分别使用了常规自抗扰算法、滑模自抗扰算法、GWO算法改进的滑模自抗扰算法控制电机模拟细纱卷绕。首先时间为600 ms时,改变转速到18 300 r/min,其次时间为800 ms时,改变转速到18 600 r/min,模拟纱线在卷绕过程中所需对应变动的卷绕速度。通过Simulink进行仿真验证,得到永磁同步电机在3种不同算法控制下的转速、转矩波动曲线,并对结果进行对比分析。图4为3种不同算法控制下的电机转速波动曲线。
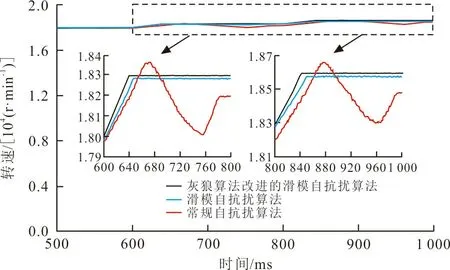
图4 电机转速波动曲线Fig.4 Motor speed fluctuation curve
从图4可以看出,3种控制方法都能使永磁同步电机达到稳定运行的状态,但是各种方法控制下的控制精度、调速时间、电机运行的稳定性,以及系统的抗干扰能力都有差异。
在常规自抗扰算法控制下,转速出现了明显的超调,第1次超调过后转速稳定在18 195 r/min左右,第2次稳定在18 484 r/min左右。
在滑模自抗扰算法控制下,采用扩张状态观测器补偿了系统的不确定扰动,用改进滑模控制代替了状态误差反馈控制环节,因此,永磁同步电机在2次调速后的转速曲线几乎都没有超调,调速后转速稳定值由18 195、18 484 r/min,提高到了18 280、18 570 r/min,更加接近实验的设定值,在自抗扰控制的基础上提高了系统的控制精度。但是系统的抗干扰能力和调速性能有待提高。
而在GWO算法改进的滑模自抗扰算法控制下,超调最小。改进型趋近律滑模控制收敛速度快,且改进了非线性收敛因子的GWO算法寻优能力更强,因此电机调速后转速波动时间变短,由180 ms减小到40 ms,达到稳定运行的速度更快,并且转速分别稳定在18 295 r/min和18 590 r/min,更接近实验设定的期望转速。GWO算法改进的滑模自抗扰算法能有效提高系统的响应速度和控制精度。转速波动的减小就尽可能地避免了短暂卷绕速度不匹配、成纱捻度不一致、成纱质量较差等问题。
在同等实验条件下,分别用3种控制方法模拟纱线卷绕过程,测得电机调速时转矩波动曲线。图5为永磁同步电机在常规自抗扰算法控制下电机转矩波动曲线。

图5 自抗扰算法控制的电机转矩波动曲线Fig.5 Motor torque fluctuation curve controlled by active disturbance rejection algorithm
从图5可以看出,永磁同步电机在常规自抗扰算法控制下,第1次调速时转矩波动峰值达到了157 mN·m,第2次调速时转矩波动峰值达到了153 mN·m,瞬时平均转矩增量为105 mN·m;
图6为永磁同步电机在滑模自抗扰算法控制下电机转矩波动曲线。
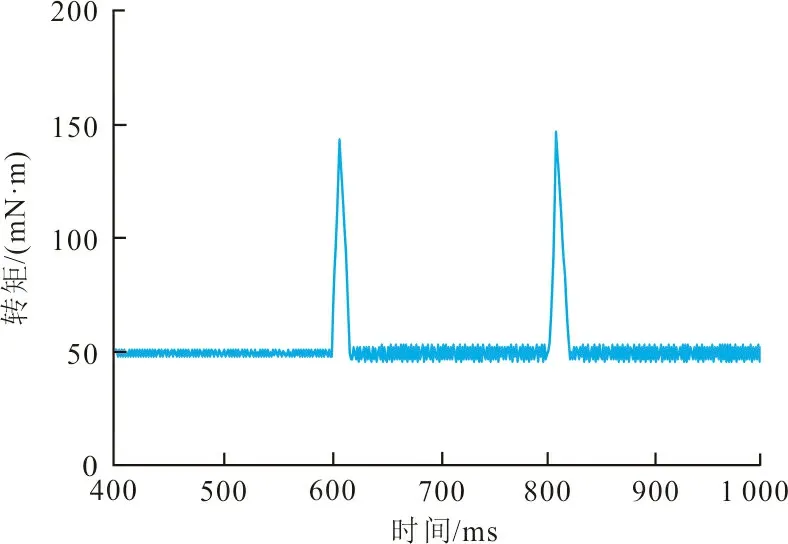
图6 滑模自抗扰算法控制下的电机转矩波动曲线Fig.6 Motor torque fluctuation curve controlled by sliding mode active disturbance rejection algorithm
从图6可以看出,在滑模自抗扰算法控制下,第1次调速时转矩波动峰值减小到了141 mN·m,第2次调速时转矩波动峰值减小到了139 mN·m,瞬时平均转矩增量减小到90 mN·m。通过比较调速时的电机转矩脉动增量可知,引入了滑模控制的自抗扰算法在调速时,对永磁同步电机转矩脉动有抑制作用,瞬时转矩增量减小了14.28%。在滑模自抗扰算法控制下,利用滑模控制鲁棒性高的特点,能有效提升系统的抗干扰能力。
图7为永磁同步电机在GWO算法改进的滑模自抗扰算法控制下电机转矩波动曲线。

图7 改进GWO算法的滑模自抗扰算法控制下的电机转矩波动曲线Fig.7 Motor torque fluctuation curve underthe control of sliding mode active disturbance rejection algorithm under improved GWO algorithm
从图7可以看出,GWO算法改进的滑模自抗扰控制算法控制下,第1次调速时转矩波动峰值仅有118 mN·m,第2次调速时转矩波动峰值仅有122 mN·m,瞬时平均转矩增量为70 mN·m。
在GWO改进的滑模自抗扰算法控制下,利用滑模控制鲁棒性高的特点,提升了系统的抗干扰能力,利用GWO算法对滑模控制的参数进行寻优,保证了参数的精确性,解决了滑模控制参数由于设定不精确,导致系统响应速度不高且抖振明显的问题,因此电机调速时的瞬时平均转矩增量由105 mN·m减小到70 mN·m,减小了约33.33%,且在调速时电机的转速波动减小,系统的调速性能提高。该控制方法相较于滑模自抗扰控制,能有效增强系统的鲁棒性。
通过对比3种不同算法控制下的电机转矩波动曲线可以看出,电机在常规自抗扰算法控制下瞬时转矩增量最大,滑模自抗扰算法控制下次之,而GWO算法的滑模自抗扰控制算法控制下转瞬时矩增量最小,且随后伴随的转矩脉动最小,电机在整个运行过程中最平稳。
实验证明,改进GWO算法优化下的基于增益可调扩张状态观测器与改进型趋近率滑模控制联合改进的自抗扰控制策略可有效抑制系统的转矩脉动,提高成纱质量,减少纱线断头。
4 结 语
本文针对永磁同步电机驱动细纱机卷绕系统调速后的转速、转矩波动,导致管纱质量不高或纱线断头问题,提出了改进GWO算法优化下的基于增益可调扩张状态观测器与改进型趋近率滑模控制联合改进的自抗扰控制策略。通过搭建永磁同步电机仿真模型,验证了所提出的控制策略可以降低永磁同步电机转速、转矩的波动。实验表明,改进GWO算法优化下的基于增益可调扩张状态观测器与改进型趋近率滑模控制联合改进的自抗扰控制策略对系统转速、转矩波动降低效果显著,提高了管纱的质量,减少了细纱机卷绕过程中纱线断头的产生。

