基于深度置信网络的缝纫平整度客观评价模型

胡 胜,张佳琪,张 溪,高冰冰

(西安工程大学 机电工程学院,陕西 西安 710048)

0 引 言

服装加工过程中,受材料性能差异、洗涤温度、时间和外力等多重因素影响而产生的缝纫线两侧的褶皱,称为缝纫平整度。缝纫平整度作为评价织物质量的关键要素,其评判准确性与否直接影响织物外观质量[1]。目前主要通过将试样与标准缝纫平整度图样作对比进行平整度评价。但该方法易受到检测环境和个人主观臆断等的影响,导致评价结果不理想。借助人工智能和图像处理技术,快速准确地对织物缝纫平整度进行客观评价,可避免主观因素影响,提高评价正确性[2]。因此,如何建立基于人工智能的织物缝纫平整度客观评价模型对改进织物外观质量具有重要价值。

目前,国内外学者围绕织物平整度评价进行了深入研究。文献[3]研究发现缝纫线的弹性应变是决定缝纫线产生缝褶倾向的关键因素,织物和缝纫线的拉伸性能的一致性是改善接缝外观和获得光滑接缝的关键参数。文献[4]利用织物厚度、织物重量、织物经密度、缝纫线断裂伸长率、针迹密度和缝纫种类等6个参数,评价缝纫平整度。文献[5]等利用Gabor变换提取了不同方向、不同频率的6个总熵值,并构建二次多元回归模型评价缝纫平整度。文献[6]选择线张力、压脚压力和针迹长度作为参数,利用基于式样三维形状的分形维数评价缝纫平整度等级。文献[7]提出了一种基于灰度共生矩阵、小波分析和BP神经网络的织物缝纫平整度的自动评估方法。文献[8]通过计算待测图像的派生输入向量和加权训练图像之间的标量积,然后利用傅里叶变换与无监督神经网络卡霍南Map实现缝纫平整度评价。文献[9]针对服装图案识别准确度问题,改进了SSD网络模型,预测精准度提升3.63%。文献[10]采用小波独立混合模型和布质纹理等提取缝纫图像特征参数,然后采用模糊分类器评价缝纫平整度。文献[11]从样品3D模型的2D图像提取多尺度小波分析、光谱分析、纹理分析和分形分析等特征向量,并建立了缝纫平整度评价模型。文献[12]使用平滑轮廓中提取了5个特征,并创建了一个人工神经网络分类器,实现了平整度等级的自动评估。文献[13]构建了依据模型曲率均值的缝纫平整度客观评价模型。文献[14]建立一个基于有序逻辑回归模型的接缝皱褶自动评估系统,该系统使用视觉信息和回归技术自动评估缝纫平整度等级。文献[15]提出了基于修正的二维经验模态分解的服装缝纫线平整度评估方法,该方法可选择二维IMF和ABEMD的残差来表示服装的缝纫针迹外观。文献[16]利用Faster R-CNN网络检测织物表面目标,该方法的精准度达84.89%。

上述研究表明,目前针对织物缝纫平整度评价主要集中在基于图像部分特征参数构建缝纫平整度评价模型,缝纫图像褶皱程度表征不够全面,模型的评价精度不高,约为90%[7]。鉴于此,本文提出一种融合特征参数与DBN的缝纫平整度客观评价方法,利用灰度共生矩阵提取特征图像参数,构建基于DBN的平整度评价模型,实现织物缝纫平整度自动评价。

1 织物缝纫图像特征参数提取

进行缝纫平整度评价时,首先采用图像灰度化处理、中值滤波去噪、直方图均衡强化等方法对织物缝纫图像进行预处理,获取更高质量的织物特征图像。然后提取缝纫图像特征,而纹理特征是基于图像灰度按一定的规律在图像物体表面频繁出现形成的图像物体固有属性,描述的是图像灰度像素重复变化。

本文采用灰度共生矩阵方法提取织物缝纫图像特征参数,其本质是通过统计2个像素点之间的相关性来反映目标图像的纹理特征[17]。假设f(x,y)是一幅灰度级别L的二维图像,则其灰度共生矩阵表达式[18]为

P(i,j,d,θ)={(x,y),(x+Δx,y+

Δy)|f(x,y)=i,f(x+Δx,y+Δy)=j}

(1)

式中：P为L×L的矩阵;d为在θ方向上,2个像素点之间的距离,即矩阵的统计步长;Δx和Δy为偏移量,满足Δx=dcosθ,Δy=dsinθ。

在此基础上,能量、熵、对比度和相关性4种纹理特征值可表示为

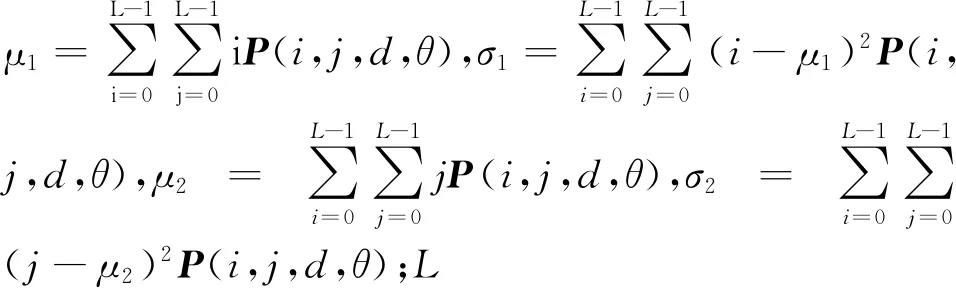
在提取的缝纫图像特征参数中,能量特征参数表征的是缝纫图像灰度分布的杂乱程度。图像纹理越无规律越粗糙,能量越大,此时图像灰度分布越随机;反之若图像灰度呈现均衡状态,纹理简单,则能量值较小。熵特征参数表示缝纫图像的复杂程度。熵值越大,图像越复杂、随机,图像各处灰度共生矩阵值越接近;反之熵值越小,则说明图片简单或规律。对比度参数刻画的是2个像素点间纹理灰度值和可视化程度的差异大小。对比度越大图像纹理凹槽越深刻,视觉效果好;反之对比度越小则说明图像中纹理凹槽浅淡,视觉体验效果模糊。相关性参数体现的是缝纫图像局部灰度的相关性,相关性越大说明图像中局部区域的相似程度越高[21]。

2 织物缝纫平整度评价模型构建

2.1 基于DBN的织物缝纫平整度评价建模

织物缝纫图像的特征参数与缝纫平整度等级之间存在着一定的相关关系,因此,可以将基于特征参数的平整度评价问题转化为多维非线性空间分类问题。DBN是使用概率生成输出的学习算法,是一种由多个受限玻尔兹曼机(restricted Boltzmann machine, RBM)堆叠而成的深度学习网络[22],在非线性系统建模中表现出优异的拟合能力,能很好地适应多分类问题。鉴于此,本文构建基于DBN的缝纫平整度评价模型[23],如图1所示。

图1 用于织物缝纫平整度评价的DBN结构Fig.1 DBN structure for the evaluation of sewing flatness

图1中,DBN的结构由多个相互连接的RBM组成。第1个 RBM 单元是可见层,后面的是隐藏层,且单个RBM结构由一层可见层与隐藏层组成。两层RBM之间的神经元是全连接的,然而同层神经元之间没有联系。

可见层和隐含层之间的能量关系[24]可表示为

式中：vi和hi为输入神经元和输出神经元的状态;wij为神经元间的权值;bi和aj分别为可见层和隐含层的偏置;α为每层RBM连接权重和偏置的组合。

较低的能量代表DBN模型达到理想状态,即代表缝纫平整度客观评价模型误差较小。可见层和隐含层的联合分布公式可表示为

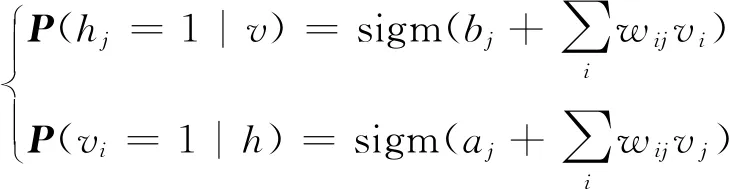
(4)

式中：sigm(t)=1/[1+exp(-t)]为激活函数。

因此,构建缝纫平整度客观评价模型就是寻找每层RBM连接权重和偏置的组合α={w,a,b}。使用非对数似然函数作为训练过程中的目标函数Q,可表示为

(5)

在无监督训练阶段,使用贪婪算法对RBM逐层训练,将上一层RBM训练后的隐藏层作为下一层RBM的输入,以此实现RBM的最优。在有监督训练阶段,采用BP算法预测RBM所提取的深度特征,基于预测误差调整网络参数,确保DBN预测结构整体最优,获得符合精度要求的缝纫平整度客观评价模型。

2.2 织物缝纫平整度评价策略

根据上节的分析,本文提出的织物缝纫平整度评价策略为：首先需要对缝纫图像进行灰度化处理、滤波法降噪和直方图均衡化等预处理,然后利用灰度共生矩阵提取能量、熵、对比度和相关性等关键特征参数;在此基础上构建基于DBN的织物缝纫平整度评价模型,并训练该评价模型以符合精度要求,接下来利用测试图像检验模型有效性;最后提取待测图像的相关特征参数,输入客观评价模型求解。为了给出待测图像的平整度等级,本文将织物缝纫平整度等级设为SS-5、SS-4、SS-3、SS-2和SS-1级共5个等级,对应客观评分区间分别为：[0,2]、(2,4]、(4,6]、(6,8]和(8,10][25]。

3 实例分析

3.1 织物缝纫样本预处理

为验证所提方法的有效性,首先对不同程度褶皱的织物缝纫样本,按照标准对照法进行量化打分,得到样本量化信息如图2所示。

图2 样本量化信息表Fig.2 Information table of sample quantification

图2中,图样下边数字代表该图样的缝纫平整度主观评分,同一行缝纫平整度等级相同,从上至下平整度等级分别为SS-5～SS-1级。

然后对获取的缝纫图像依次进行灰度化处理、滤波去噪、直方图均衡化增强预处理,结果如图3所示。

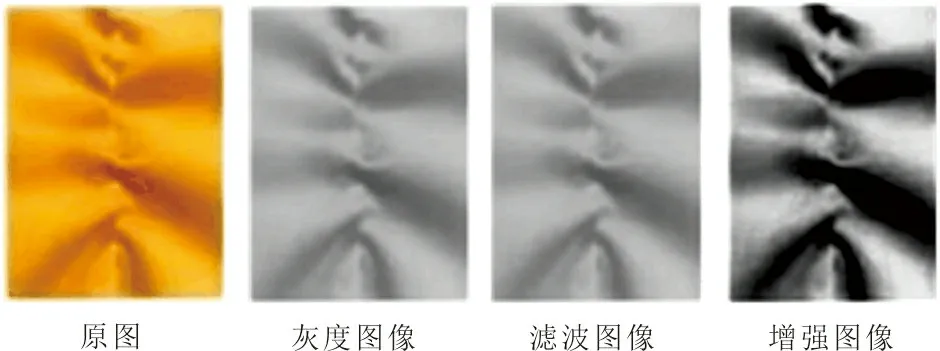
图3 织物缝纫图像预处理Fig.3 Fabric sewing image preprocessing

从图3可以看出,经过预处理后的图像缝纫线附近的明亮区域与阴影区域对比明显,缝纫图像褶皱程度更加清晰且易于分辨,图像质量更高,利于后续提取图像的相关特征参数。

3.2 图样特征参数提取

在获取增强图像基础上进行织物缝纫特征参数提取,将图像灰度矩阵所有像素值除以64并向下取整作为新的灰度级数,并依据式(1)分别计算水平方向(0°)、垂直方向(90°)、对角线方向(45°、135°)的4个灰度共生矩阵,并利用式(2)计算能量、熵、对比度、相关性4个特征参数,同时剔除样本3、8、13、15、18等偏离正常数据的5个样本。对剔除异常样本后的20个样本进行统计分析,同时给出织物缝纫平整度的主观评分结果,如表1所示。

表1 特征参数计算结果Tab.1 Calculation results of characteristic parameters

3.3 基于DBN的织物缝纫平整度客观评价模型

进行缝纫平整度客观评价建模时,随机选取4个不同平整等级的16个样本用于训练缝纫平整度客观评价模型,剩余4个样本用于测试。设置DBN模型的参数：训练步数为100,隐藏层节点数分别取43、57、39、41。DBN评价模型训练结束后,使用测试集数据进行DBN的织物缝纫平整度客观评价模型测试评价。

基于DBN的缝纫平整度客观评价模型对检验样本的输出结果如图4所示。

图4 基于DBN缝纫平整度测试结果Fig.4 Sewing flatness test results based on DBN

从图4可以看出,构建的DBN模型平整度客观评分与主观评分基本重合,进一步基于式(6)计算得到DBN模型的评价精度达到98.74%,说明构建的基于DBN的织物缝纫平整度客观评价模型可以有效客观评价织物的缝纫平整度等级。

3.4 评价模型有效性对比

为验证DBN缝纫平整度客观评价模型的有效性,采用多元回归模型的缝纫平整度评价模型进行对比实验。构建织物平整度评价的多元回归模型时,首先计算主观评分与能量、熵、对比度、相关性4个特征参数的皮尔逊相关系数,分别为-0.816、0.789、-0.115、0.482。

可以看出,主观评分与能量和熵的相关系数达到-0.816和0.789,且分别呈现出显著负相关和显著正相关关系,故提取能量和熵2个参数对表2中的样本数据进行平整度评价模型拟合。拟合效果如图5所示。

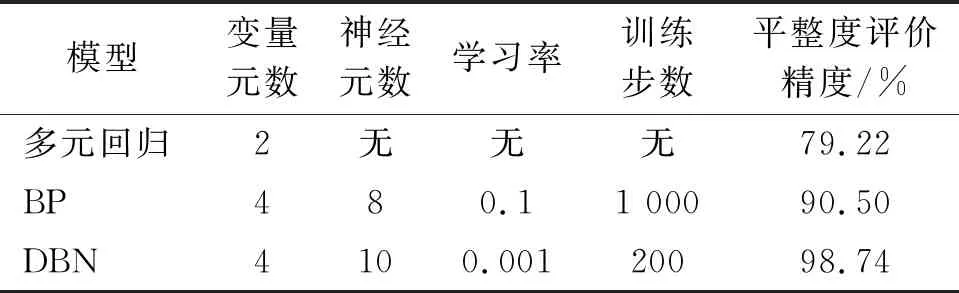
表2 不同算法的缝纫平整度评价结果对比Tab.2 Comparison of sewing flatness evaluation results of different algorithms

图5 基于多元回归的平整度评价模型拟合效果Fig.5 The fitting effect of the flatness evaluation model based on multiple regression

从图5可以看出,除少部分样本点没有被拟合成功外,其他大部分样本均在回归曲线上,拟合效果良好,据此输出织物平整度评价的多元回归模型客观评分可表示为

y=756.3+507.6×xASM-486.3×xENT-

式中：y为缝纫平整度客观评分;xASM为图像能量值;xENT为图像熵值。

经过测试,利用式(6)计算得到该多元回归模型的评价精准度约为79.22%。

进一步采用基于BP神经网络与构建的多元回归模型、DBN进行效果对比,模型参数设置及不同算法的缝纫平整度评价结果如表2所示。

从表2可以看出,多元回归建模时因只提取2个主要影响特征参数进行拟合,导致其不能完全表征缝纫图像特征使得评价精度不甚理想。相比浅层BP神经网络,构建的深度DBN模型具有较强的特征提取能力,对缝纫平整度评价精度更高。说明本文提出的融合特征参数和DBN模型对织物的缝纫平整度具有较好的评价性能。

4 结 语

针对织物缝纫平整度主观评价精度较低的问题,本文构建了融合特征参数与DBN的织物缝纫平整度评价模型。

1) 利用灰度共生矩阵提取的能量、熵、对比度和相关性等特征参数能够较好地度量织物缝纫平整程度差异性。

2) 建立的DBN缝纫平整度评价模型,实现了织物缝纫平整度的客观评价。

后续将在本文研究的基础上,深入分析不同面料、缝纫样式、缝纫线颜色等场景下的织物缝纫平整度客观评价,提升其评价模型的普适性与准确性。