不规则混凝土壳体收缩徐变效应的有限元分析

熊高亮

(江西省交通设计研究院有限责任公司,江西 南昌 330052)

0 引言

收缩徐变是混凝土本身的固有特性,会导致混凝土结构应力和变形随时间而改变,对结构的受力性能及长期变形影响很大[1],有时甚至成为导致结构物开裂破坏的关键因素,特别是对于大体积、大面积混凝土结构,收缩徐变效应更为显著。

混凝土结构收缩徐变的研究较为复杂,国内外对此展开了很多研究,张运涛等在高性能混凝土收缩徐变模型试验研究的基础上,开展了自然环境下高性能混凝土双悬臂构件的长期性能试验研究[2],李达等对简支组合梁在长期变形下混凝土的收缩模式进行了相关研究[3],熊学玉等[4]对某预应力梁在混凝土收缩徐变效应作用下的真实反应进行测试并分析实测数据,郑怡等通过实验研究了机制砂混凝土梁收缩徐变[5],Warner,Robert F[6]和Asamoto,Shingo等[7]对混凝土梁的徐变效应进行了相关分析。

国内外对混凝土收缩徐变的研究对象多为桥梁和规则的梁、板结构,对不规则混凝土壳体的收缩徐变效应的研究相对较少。本文以一实际工程为背景(见图1),结合收缩和徐变等相关知识,运用有限元软件,研究该不规则混凝土壳体在自重作用下的收缩徐变效应,将其应力及应变情况与不考虑收缩徐变时的结果进行对比分析,总结收缩徐变效应对该壳体的影响,为类似结构的设计提供一定的参考。

1 混凝土收缩徐变的理论计算

1.1 收缩应变的计算

混凝土的收缩是指混凝土在凝结硬化及使用过程中,由于混凝土内部水分变化、化学反应及温度变化等所引起的体积减小的现象。混凝土第一年的收缩应变约为(0.2-0.4)×10-3,其80%～90%可在前6个月内完成,一年以后收缩仍有发展,但不明显[8],因此本文研究壳体竣工一年后的收缩效应,混凝土的收缩应变可按式(1)—式(5)计算[9]:

εcs(t,ts)=εcs0·βs(t-ts)

(1)

εcs0=εs(fcm)·βRH

(2)

εs(fcm)=[160+10βsc(9-fcm/fcm0)]×10-6

(3)

βRH=1.55×[1-(RH/RH0)3]

(4)

(5)

其中,t为计算考虑时刻的混凝土龄期,d;ts为收缩开始时的混凝土龄期,d,可假定为3 d～7 d;εcs(t,ts)为收缩时间发展的系数;fcm为强度等级C20—C50混凝土在28 d龄期时的平均立方体抗压强度,MPa,fcm=0.8fcu,k+8 MPa;fcu,k为龄期28 d,具有95%保证率的混凝土立方体抗压强度标准值,MPa,本文为35 MPa;βRH为与年平均相对湿度相关的系数,式(1)—式(4)适用于40%≤RH<90%;RH为环境年平均相对湿度,%;βsc为依水泥种类而定的系数,对一般的硅酸盐类水泥或快硬水泥,βsc=5.0;h为构件理论厚度;h=2A/u,A为构件截面面积,u为构件与大气接触的周边长度,本文计算得h=125 mm。

其他相关参数取值如下RH0=100%,h0=100 mm,t1=1 d,fcm0=10 MPa;本文中t=365 d,ts=3 d,RH取55%,通过以上公式计算可得,εcs(t,ts)=0.351×10-3,此结果与前文提到的混凝土第一年的收缩应变约为(0.2～0.4)×10-3相符,表明结果的合理性。

本文在研究壳体的收缩效应时,结合温度变化等效混凝土收缩[10]的思想,由计算得到的收缩量,通过ε=αΔT(其中,α为膨胀系数,取1×10-5/℃;T为温度,℃,转换为温度的变化来等效收缩作用。

1.2 徐变系数的确定

混凝土在长期持续荷载作用下,应力不变,变形也会随时间而增长,这种现象称为混凝土的徐变。徐变在早期发展较快,一般在最初六个月内可完成最终徐变的大部分(约70%～80%),一年可完成约90%,最终总徐变应变值为瞬时应变的2倍～4倍。

通常混凝土的徐变采用徐变系数φ(t,t0)来描述[11]。由规范查得混凝土的徐变系数可按式(6)—式(12)计算:

φ(t,t0)=φ0·βc(t-t0)

(6)

φ0=φRH·β(fcm)·β(t0)

(7)

(8)

(9)

(10)

(11)

(12)

其中,t0为加载时的混凝土龄期,d;t为计算考虑时刻的混凝土龄期,d;φ(t,t0)为加载龄期为t0,计算考虑龄期为t时的混凝土徐变系数;φ0为名义徐变系数;βc为加载后徐变随时间发展的系数。

由于徐变是一种长期效应,而对于本文所研究的壳体来说,自重作用在壳体上的时间最为长久,所以本文仅研究壳体在自重作用下的徐变效应。在本文当中,RH0=100%,h0=100 mm,t1=1 d,fcm0=10 MPa;t=365 d,t0=3 d,h=125 mm,RH取55%,fcm=36 MPa,由以上公式计算得φ(t,t0)=3.120。

本文基于有效模量法[12]的思想,在其基础上进行一定的改进,在有限元分析时结合Abaqus中的混凝土塑性损伤模型,将按照有效模量法计算出的弹性模量代替该模型中初始弹性模量,进而对不规则混凝土壳体的徐变效应进行研究。

2 壳体在收缩作用下的有限元分析

2.1 收缩作用下壳体内表面的应力分析

在收缩作用下,不规则混凝土壳体内表面的最大主应力云图如图2,图3所示。

从图2,图3中可以看出,在收缩作用下,不规则混凝土壳体顶部的最大主应力较小,一般都低于0.306 MPa,而壳体最底部受约束的部位,在壳体收缩的过程中受到较大的约束作用,混凝土处于明显的受拉状态,最大主应力较大,大部分都超过了0.611 MPa;在门窗洞口附近部分区域由于局部几何形状的原因存在应力集中现象,最大主应力较大,其中有一些部位的最大主应力值超过了3.056 MPa。整个壳体内表面应力的最大值3.667 MPa,位于图3壳体的最左端,此处不仅离底端约束近,且在窗洞口附近,同时此处的曲率相对较大,所以当混凝土壳体发生整体收缩时,此处的最大主应力值最大。

2.2 收缩作用下壳体外表面的应力分析

在收缩作用下,不规则壳体外表面的最大主应力云图如图4,图5所示。

从图4,图5中可以看出,在收缩作用下,壳体的外表面最大主应力较大的部位主要分布在壳体下端的窗洞口附近,应力值一般都大于1.580 MPa,这些区域由于洞口的存在,收缩量相对更大,因而在壳体发生收缩时,产生较大的拉应力;除此以外的大部分区域,最大主应力值都相对较小,均低于0.632 MPa;整个外表面的最大主应力值为3.792 MPa,位于图4中壳体最右边的窗洞口的右下端。通过以上分析,可以发现,该壳体受收缩作用的影响较为明显,在收缩作用下,壳体表面的最大主应力值较大,在工程设计中不容忽视。

3 壳体在徐变作用下的应力应变分析

3.1 壳体考虑徐变作用时的有限元分析

通过有限元计算,在自重作用下,考虑混凝土徐变效应后,该不规则混凝土壳体内外表面的最大主应力云图如图6—图9所示。

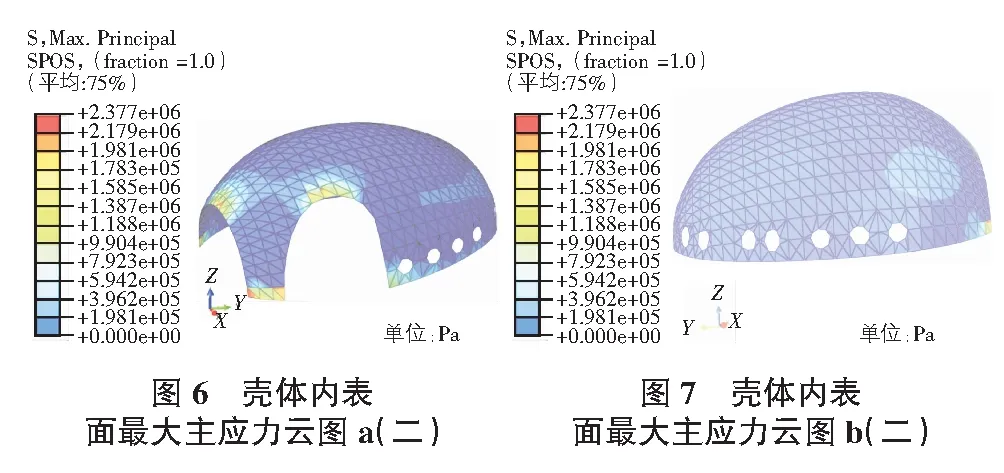
在图6中,两个大洞口的底端和顶端的小部分区域,在自重荷载的作用下发生较大的变形,壳体内表面的最大主应力相对较大,其值在1.188 MPa以上;其余部分的最大主应力分布情况较为均匀,且应力值较小,大部分不超过0.198 MPa。整个壳体在自重作用下内表面最大主应力的最大值为2.377 MPa,对应部位见图6中壳体左边大洞口的右下端。在图7中,只有最右下端靠近洞口的小部分区域的最大主应力值较大,最大主应力值为0.990 MPa;其他区域的最大应力值均较小,一般低于0.396 MPa。

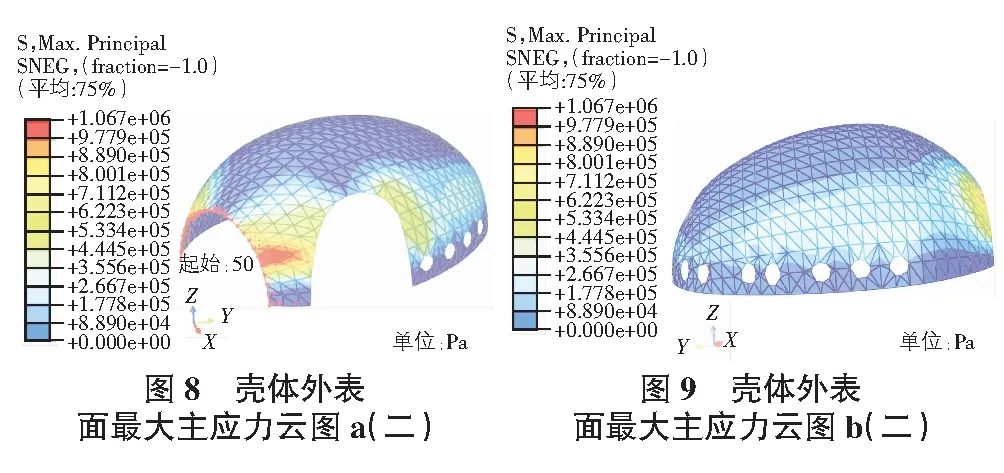
图8中,壳体侧面的最大主应力值相对较大,该区域的最大主应力值都在0.267 MPa以上,而壳体顶端区域和最下端区域的最大主应力值较小,其最大主应力均小于0.177 MPa。在两个大洞口的左右两侧区域的最大主应力值相对较大,该区域的最大主应力值均在0.445 MPa以上;特别是两个大洞口之间的区域,该处的最大主应力值比壳体其他区域的最大主应力值都要大,一般都超过了0.533 MPa,在自重作用下,整个壳体外表面最大主应力值最大的部位即位于该区域,其值为1.067 MPa。在图9中,图中最右端靠近大洞口附近区域的最大主应力值较大,其中最大值为0.889 MPa;沿壳体侧面自右向左逐渐减小,一直减小到图中最左端部位的0.267 MPa;而壳体顶部和底部的最大主应力值相对较小,一般小于0.178 MPa。

3.2 徐变对壳体应力应变的影响

运用有限元软件计算该不规则混凝土壳体在不考虑徐变效应时,内外表面的最大主应力情况,并将其与前文考虑徐变作用时壳体内外表面的最大主应力云图进行对比分析。定义图8中壳体左边大洞口边界线自左向右为路径a(如图8红线所示),分析壳体内外表面最大主应力在考虑徐变前后沿路径a的变化。

从图10,图11中可以看出,考虑徐变作用前后,壳体内外表面最大主应力沿路径a的分布曲线走势大致相同,只是考虑徐变后的应力值普遍比未考虑徐变时的应力值要大,由此也可以看出徐变效应对建筑物的不利影响。现将壳体在自重作用下考虑和未考虑徐变作用时,内外表面的最大主应力值进行对比,见表1。

表1 徐变对内外表面最大主应力的影响 MPa

通过对比发现,考虑徐变效应后,壳体内外表面的最大主应力值的峰值都有所增大,内表面增大了0.405 MPa,外表面增大了0.164 MPa。

调取考虑徐变前后壳体在最大主应力方向上的应变值进行对比,得到的具体情况见表2。

表2 徐变对内外表面最大应变值的影响

对比发现,考虑壳体的徐变作用以后,最大应变值明显增大,壳体内表面的最大应变值是没有考虑徐变时最大应变值的3.165倍,外表面的最大应变值是没有考虑徐变时最大应变值的2.865倍。由此可以看出,徐变对于该混凝土壳体的作用很明显,使得该壳体的应力应变明显增大,在实际工程设计中应当给予重视。

4 结论

本文通过运用与收缩相关的理论知识,计算出一个不规则混凝土壳体建成一年后的收缩应变,运用降温等效的思路对壳体进行收缩作用下的有限元分析;通过规范提供的方法计算出该壳体建成一年后混凝土的徐变系数,基于有效模量法的思想计算该壳体的徐变效应,得出以下结论:

1)不规则混凝土壳体在建成一年后,收缩应变为0.351×10-3。在收缩作用下,不规则混凝土壳体顶部的最大主应力较小,而下部四周门窗洞口附近及壳体最底部受约束处的最大主应力较大,整个壳体的最大主应力值为3.792 MPa,位于壳体外表面大窗洞口的右下端。

2)不规则混凝土壳体建成一年后对应的徐变系数为3.120,在自重作用下,考虑徐变效应后,壳体内表面的最大主应力在两个大洞口的底端和顶端的小部分区域较大,最大值2.377 MPa;壳体外表面两个大洞口之间的区域的最大主应力值较大,外表面最大主应力值为1.067 MPa。

3)考虑徐变效应前后,壳体表面的最大主应力分布情况大致相同,但考虑徐变效应后,壳体内外表面的最大主应力值的峰值普遍有所增大,内表面最大主应力的峰值增大了0.405 MPa,外表面的峰值增大了0.164 MPa。在考虑徐变效应以后,壳体内表面的最大应变值是没有考虑徐变时最大应变值的3.165倍,外表面的最大应变值是没有考虑徐变时最大应变值的2.865倍。