深刻理解定义 巧妙应对抛物线问题

刘力芳

(寻甸县第二中学,云南 昆明 655214)

解题是数学学习中一个永恒的话题,数学学习离不开解题.定义通常是人们对某一对象的本质属性的刻画,它是人们对一个事物进行判断和推理的基础.数学中的定理、性质、公式和法则都是在定义和公理的基础上推演出来的.每一个知识领域的学习,一般都会从其基本概念入手,之后才逐步层层展开.概念学习是数学学习的一个重要内容,只有正确理解、深刻领悟,才能掌握数学的本质.因此,概念教学是数学基础知识和基本技能教学的核心.要弄明白一个概念的本质、内涵以及外延,少不了对概念的应用,在应用中学习,在应用中加深理解.

1 利用抛物线定义求轨迹方程

例1求与圆C:(x+2)2+y2=1外切,且与直线x=1相切的动圆圆心M的轨迹方程.

解析设动圆半径为r,由动圆M与圆C外切知,|MC|=r+1,由动圆M与直线x=1相切知, 点M到直线x=1的距离为r, 把直线x=1向右平移1个单位,得到直线x=2.

从而点M到直线x=2的距离为r+1.

所以动圆圆心M到点C(-2,0)的距离与到直线x=2的距离相等.

根据抛物线的定义知,动圆圆心M的轨迹是抛物线,其中焦点为(-2,0),准线方程为直线x=2,焦点到准线的距离是4,因而p=4.

所以动圆圆心M的轨迹方程为y2=-8x.

点评本题考查了圆与圆相切、直线与圆相切的位置关系,以及抛物线的定义及其标准方程.由抛物线的定义知,“动圆圆心M的轨迹是以(-2,0)为焦点,以直线x=2为准线的抛物线”是解题的关键.本题当然可以将点M满足的条件用坐标表示出来,化简,求得动圆圆心M的轨迹方程,但计算量相对大了一些.

A.椭圆 B.双曲线 C.抛物线 D.以上都不对

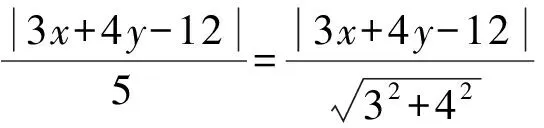
即动点M(x,y)到直线3x+4y-12=0的距离等于它到原点(0,0)的距离,由抛物线定义可知:动点M的轨迹是以原点(0,0)为焦点,以直线3x+4y-12=0为准线的抛物线.故选C.

2 利用抛物线的定义实现距离的相互转化

各种标准方程下抛物线上的点到准线的距离见表1所示:

表1 标准方程下抛物线上的点到准线的距离

表示抛物线上一点P(x,y)到准线的距离,只需要点P的横坐标(抛物线的开口向左或右时)或纵坐标(抛物线的开口向上或下时),若要表示抛物线上一点P(x,y)到焦点的距离,根据两点间距离公式,点P的横坐标和纵坐标都需要,从计算的角度看,前者更为简便.因此解题时,通常根据题意,利用定义将抛物线上的点到准线的距离与到焦点的距离进行相互转化,从而简化计算.

例3抛物线x2=4y上一点A的纵坐标为4,则点A到抛物线的焦点的距离为( ).

A.2 B.3 C.4 D.5

分析若直接求解,由点A的纵坐标为4,可求得点A的横坐标,再求得抛物线的焦点坐标,最后用两点间的距离公式求解.思路非常清晰,也很自然,但需要一定的计算量.若利用定义进行转化,则大大简化了计算.

解析抛物线x2=4y的准线方程为y=-1,由定义知,点A到抛物线的焦点的距离等于点A到准线y=-1的距离.故点A到抛物线的焦点的距离为4+1=5.

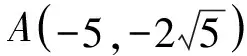
整理,得a2+10a+9=0,

解得a=-1或a=-9.

当a=-1时,F(-1,0),p=2,y2=-4x.

当a=-9时,F(-9,0),p=18,y2=-36x.

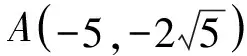
所以,所求抛物线的标准方程为y2=-4x.

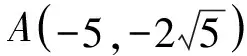
例5 斜率为1的直线l经过抛物线y2=4x的焦点,且与抛物线交于A,B两点,求线段AB的长.

分析抛物线y2=4x的焦点F(1,0),直线l经过点F(1,0),且斜率为1,故方程为y=x-1.求线段AB的长,一个极其自然的思路就是:由直线与抛物线联立方程组,求得A,B两点的坐标,再由两点间距离公式求得线段AB的长.为了体现并强调二次曲线与直线综合问题的求解通法,可以对A,B两点的坐标采用“设而不求”,利用根与系数的关系(见解法1).如果利用定义,注意到直线l经过焦点F,故|AF|等于点A到准线x=-1的距离,设A(x1,y1),B(x2,y2),则|AF|=x1+1,同理,|BF|=x2+1,所以,|AB|=|AF|+|BF|=(x1+1)+(x2+1)=x1+x2+2(见解法2).

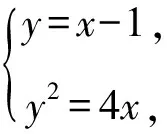
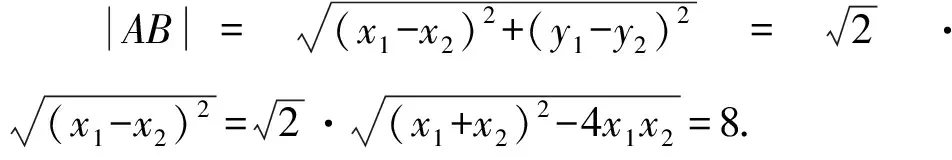
解法2 因直线l经过焦点F,所以|AF|等于点A到准线x=-1的距离,设A(x1,y1),B(x2,y2),则|AF|=x1+1,同理,|BF|=x2+1,所以,|AB|=|AF|+|BF|=(x1+1)+(x2+1)=x1+x2+2=8.

例6 在平面直角坐标系xOy中,倾斜角为α的直线m过点F(1,0),直线m与抛物线C:y2=4x交于A,B两点,抛物线C的准线为直线l.

(1)证明:以AB为直径的圆与直线l相切;

(2)若线段AB的中垂线n交x轴于点E,证明:|EF|sin2a为定值,并求出此定值.

证明注意到点F(1,0)恰好是抛物线C:y2=4x的焦点.

(1)如图1,设AB的中点为M,过点A,B,M作直线l的垂线,垂足分别为点A1,B1,M1,由定义得

|AA1|=|AF|,|BB1|=|BF|.

则|AB|=|AF|+|BF|=|AA1|+|BB1|.

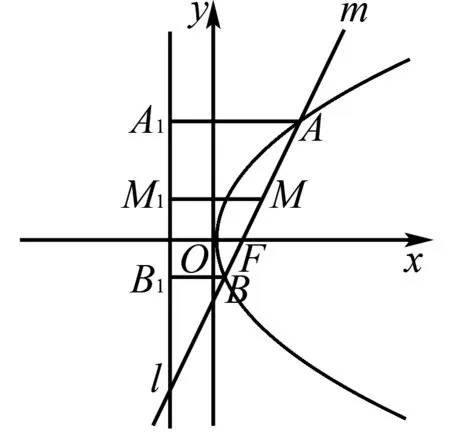
图1 例6解析图

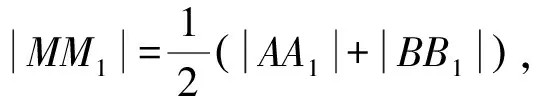
所以以AB为直径的圆与直线l相切.

(2)如图2, 因为|FA|=|AA1|=|AH|+|HA1|=|FA|cosa+2,

图2 例6解析图

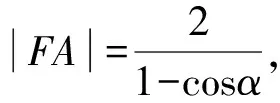
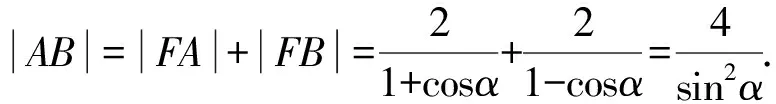
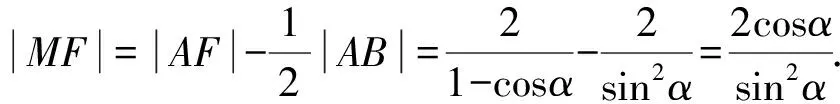
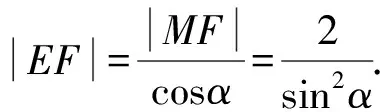
所以|EF|sin2α=2.

结论1以抛物线焦点弦为直径的圆与抛物线的准线相切.

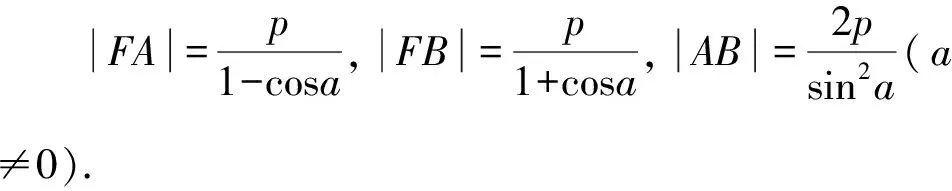
3 求与抛物线有关的最值

例7 设P是抛物线y2=4x上的一个动点,F是抛物线的焦点,

(1)求点P到点A(-1,1)的距离与点P到直线x=-1的距离之和的最小值;

(2)若B(3,2),求|PB|+|PF|的最小值.

分析两个问题分别涉及了抛物线上的点到准线的距离和到焦点的距离,由此可结合抛物线的定义进行转化,再用相关平面知识予以解决.

解析由已知,抛物线y2=4x的焦点为F(1,0),准线为直线x=-1.

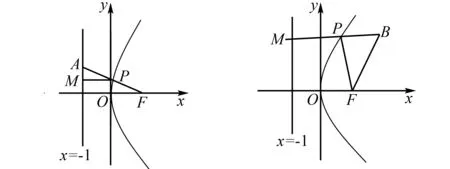
图3 例7解析图(a) 图4 例7解析图(b)

(2)如图4,BM垂直于准线,交准线于点M,交抛物线于点P,|PB|+|PF|=|PB|+|PM|,其最小值等于|BM|=4.

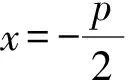
由余弦定理,得|AB|2=a2+b2-2abcos120°=a2+b2+ab=(a+b)2-ab.

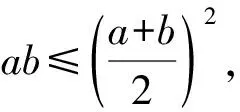
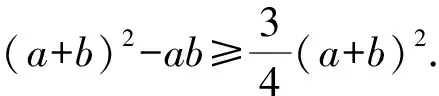
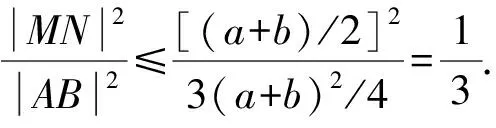
说明在抛物线中求最值,通常的解法是结合图形特征,利用抛物线的定义,将抛物线上的点到准线的距离与到焦点的距离相互转化,从而构造出“两点之间线段最短”.

深刻理解定义,在解题中灵活运用,巧妙转化,这不仅可以优化解题过程,反过来也能加深学生对知识本身的认识和掌握.教师在平时的教学中,应该以学生为中心,引导学生反复应用,组织强化训练,让学生认识到数学定义在数学学习中的重要性,从而形成良好的、科学的数学学习方法,进而发展学生的数学思维和提升学生的核心素养[1].