新题型 新视角 新方法——以一道模考题为例

孔令春

(永靖县移民中学,甘肃 临夏回族自治州 731600)

乌鲁木齐地区2023年高三年级第二次质量检测数学试卷,与教育部发布的高考信息“数学高考加入复杂情景,强调数学思想方法”很贴近.其中第15题可以说是一道难题,更应该说是一道考查数学思想方法的创新好题.此题若缺少深刻的思维,没有思想方法做指引,必将寸步难行,甚至影响后续答题.

1 题目呈现

2 解法探究

视角1 利用点在曲线上构建a,c的关系.

解法1 设c为椭圆的半焦距,由已知易得F1(-c,0),A(0,-b).

化简,得bx+cy+bc=0.

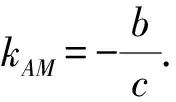
因为F2(c,0),

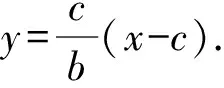
化简,得by=cx-c2.

设M(x0,y0),则N(x0,-y0).

所以bx0+cy0+bc=0,

①

by0-cx0+c2=0.

②

③

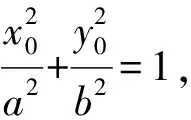
整理,得5c2=a2.

④

评析本解法学生容易想到,思路通畅.但是在③和④处的计算量是相当大的,限于篇幅,未做展示.计算能力不足的学生很可能中途放弃.作为基本功训练尚可,考场上不可取.我们必须在思想方法上下功夫,以期减少“死算”致错风险.

视角2 通过向量共线引入参数,建立e与参数的关系,进而求e.

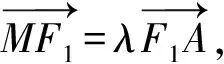
所以(-c-x0,-y0)=(λc,-λb).

因为M((-λ-1)c,λb),

所以N((-λ-1)c,-λb).

因为NF2⊥AM,所以kNF2·kAM=-1.

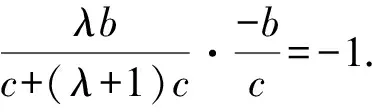
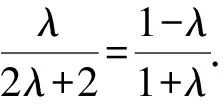
评析由于利用平面向量知识引入了参数,运算量明显减少了.本解法用到了方程思想、消元思想.将求离心率等价转化为求参数λ.这里也有整体代换的思想,不失为一种好方法,值得借鉴.

视角3 从点A的坐标入手,借助韦达定理求解.

解法3 因为A(0,-b),F1(-c,0),F2(c,0),

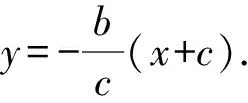
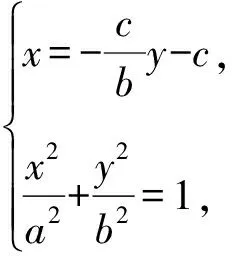
(a2+c2)y2+2bc2y-b4=0.

而yA=-b,

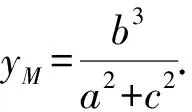
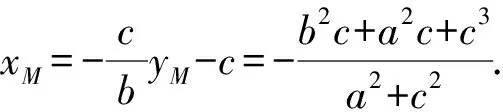
因为NF2⊥AM,所以kNF2·kAM=-1.

整理,得a2=5c2.

评析本解法充分利用了圆锥曲线的基本原理,巧妙地将复杂的坐标计算转化为直线与曲线的相交关系[1],在韦达定理的作用下快速得解.本质是思维升级,运算减量.这种方法不仅适合小题,也适合解答题.学生的这种数学意识不强,很多学生难以在考场上想到,我们需要平时的训练和积累.事实上,消去y也同样可以完成解答,有兴趣的同仁可以试试.

视角4 从几何的角度出发,利用对称关系将e几何化.

解法4 如图1,连接MN,MF2,AF2,

图1 构造直角用图

易得MN⊥PF2.

记∠PMF1=α,

由△MPF1∽△QF1F2,得∠PMF1=∠F1F2Q=α.

由△MPF1∽△F1OA,得∠PMF1=∠F1AO=α.

由对称性得

∠MF2F1=∠F1F2Q=α,∠F2AO=∠F1AO=α.

所以∠MF2Q=∠F1AF2=2α.

所以ΔMQF2∽ΔMF2A.

所以∠MF2A=∠MQF2=90°.

设|MF2|=t,则|MF1|=2a-t.

而|AF1|=|AF2|=a,

由|MA|2=|AF2|2+|MF2|2,得

(3a-t)2=a2+t2.

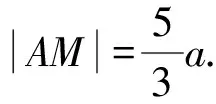
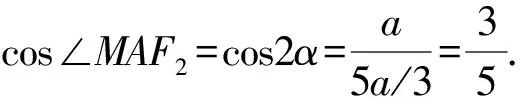
评析解析几何本质还是几何,因此在解答解析几何题目时,我们要高度关注题目所包含的几何特性.解题时利用几何关系可以省去大量的代数运算,甚至可以口算,正如本例.本题最关键的几何关系是四个等角,两组相似,挖掘出一个直角三角形.

视角5 从几何的角度考虑,利用正弦定理及椭圆的定义,将e几何化.

解法5 如图1,设∠MF2F1=α,∠F1MF2=θ,

那么∠MF1F2=π-(α+θ).

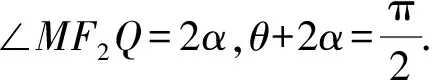
在△MF1F2中,由正弦定理,得

结合椭圆定义和几何性质,得

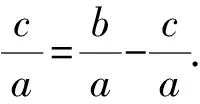
所以b2=4c2.

即a2-c2=4c2.

评析本解法充分利用了椭圆的定义和正弦定理,将代数和几何关系恰当地结合在一起,是典型的数形结合思想的应用.本解法揭示了本题的几何含义,属于求解离心率问题极致解法,避开了繁杂运算.也许命题专家就是基于此进行试题编制的.这也正是学数学的一种较高境界——厘清问题的本质.

视角6 从焦点弦出发,结合几何.

解法6 如图1,设∠MF1F2=φ,

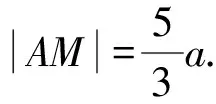
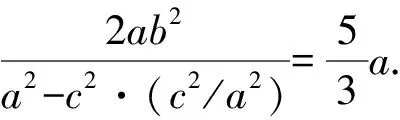
整理,得a4+5c4-6a2c2=0.

即5e4-6e2+1=0.

从解法4,5,6不难看出,利用题目中蕴含着的几何关系解题非常便捷[2],但往往难以发现几何关系,数形结合的思想方法就难以落地.下面再举一例.

分析本题背景看似是简单的三角形,实际很复杂.无论是三角形的边,还是角的数量关系都不是很清晰.已知条件很难糅合在一起,能够把这些边角关系结合起来的恰恰是题目隐藏着的几何关系.

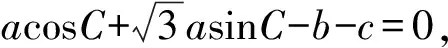
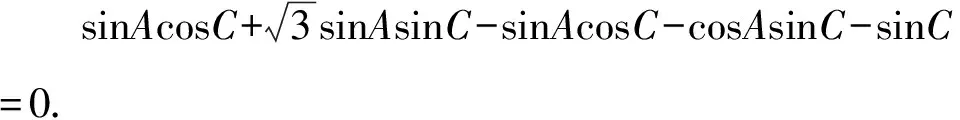
如图2,过点C作CE∥AB,CE与AD的延长线交于点E.

图2 构造相似形

设AE=x,于是在△ACE中,

结合3b+c=4整理,得

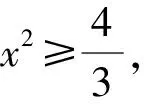
故选B.

布鲁纳认为:“掌握基本的数学思想和方法可以使得数学更加容易理解.”事实上,掌握基本的数学思想和方法才能通向思维迁移的阳光大道.在基本数学思想的指导下,运用数学方法才能驾驭数学知识,才能培养学生的核心素养.这不但使数学学习变得容易,而且会使得别的学科也容易学习.因此,数学教学不能就知识论知识,而是要使学生掌握数学最根本的东西,用数学思想和方法统领具体知识、具体解题方法,逐渐形成自身能力.