2023年全国甲卷解析几何大题的解法探究

何 勇

(白云兴农中学,贵州 贵阳 550000)

2023年全国甲卷理科数学的解析几何大题是非常不错的一道题目,该题解法多样,可用高中的多个知识点进行解答.

1 高考真题

(1)求p;

2 解法探究

2.1 第(1)问解析

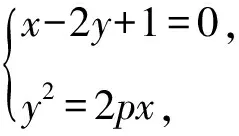
所以yA+yB=4p,yAyB=2p.

即2p2-p-6=0.

因为p>0,解得p=2．

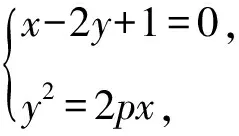
所以xA+xB=8p-2,xAxB=1.

因为p>0,解得p=2．

即2p2-p-6=0.因为p>0,解得p=2．

说明直线x-2y+1=0的参数方程有无数个[1],与所取直线上的点有关.

2.2 第(2)问解析

所以y1+y2=4m,y1y2=-4n,

△=16m2+16n>0,得m2+n>0.

所以(x1-1)(x2-1)+y1y2=0.

即(my1+n-1)(my2+n-1)+y1y2=0.

即(m2+1)y1y2+m(n-1)(y1+y2)+(n-1)2=0.

将y1+y2=4m,y1y2=-4n代入,得

4m2=n2-6n+1,即4(m2+n)=(n-1)2>0.

所以n≠1,且n2-6n+1≥0.

设点F到直线MN的距离为d,

所以k2+b2+6kb-4=0.

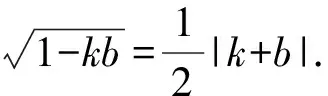
要使直线MN与抛物线有两个交点,则△=16-16kb>0.即kb<1.

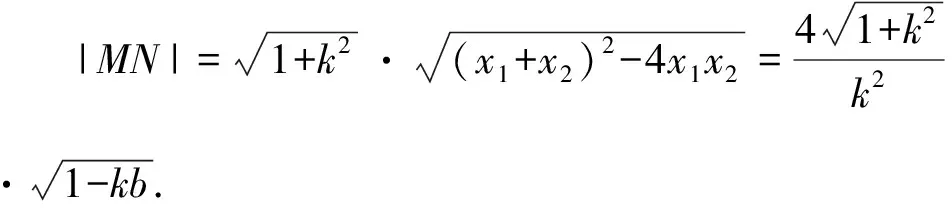
由k2+b2+6kb-4=0可得

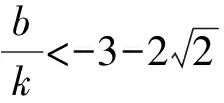
启示解法1和解法2在设直线方程形式上是不同的,直线方程的不同导致计算量和思想方法不同,在教学中要重视y=kx+b与x=ky+b两种方程的应用,选择合适的方程会大大减少计算量或者避免分类讨论的出现,提高解题的效率.

解法3设∠MFx=θ,由抛物线的焦半径可得

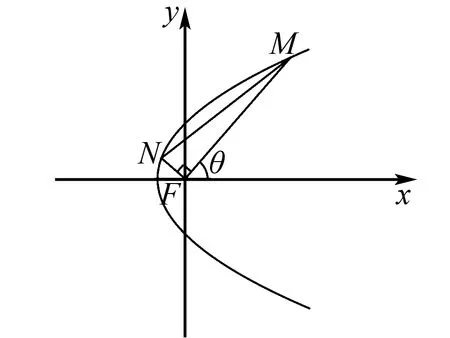
图1 平移后抛物线示意图

=4(-ρ2sinθ+1)