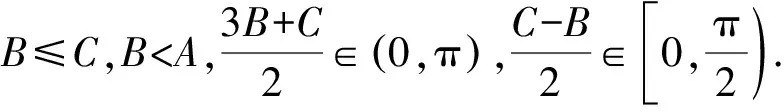2023年全国高中数学联赛(四川预赛)试题及解析
张 君
(四川省温江中学,四川 成都 611130)
2023年全国高中数学联赛(四川预赛)试题,全卷共11道题(满分120分),其中8道填空题(每小题 8 分),3道解答题(第9题16分,第11、12题各20分).笔者参考2022年四川预赛试题及其解析[1],对2023年四川预赛每道题都进行了分析和研究,逐个给出解析.
1 试题内容简析
该试题涉及函数性质(第1题),平面向量(第2题),二项式定理(第3题),函数与导数(第4题),数论(第5题),立体几何(第6题),平面解析几何(第9题),三角函数与三角变换(第7,8题),函数与数列(第5,10题),函数与不等式(第8,11题).
2 试题及其解析

解析令x=1,得2f(1)+f(0)=1.
①
令x=-1,得2f(-1)+f(0)=1.
②
令x=0,得2f(0)+f(-1)=1.
③


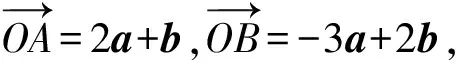
解析由a⊥b建立以O为原点,分别以向量a,b的方向为正方向建立平面直角坐标系,因为|a|=1,|b|=2,所以a=(1,0),b=(0,2).
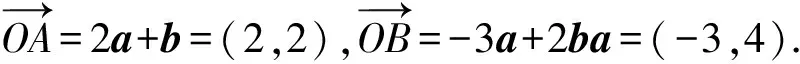
从而求得SΔAOB=7.
题3 在(-xy+2x+3y-6)6的展开式中,x4y3的系数为____. (用具体数字作答)


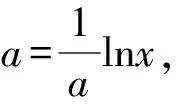
所以Q(ea2,a).



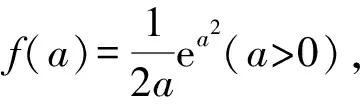



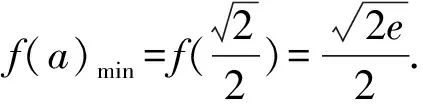
题5 设集合I={0,1,2,…,22},A={(a,b,c,d)|a,b,c,d∈I,a+d≡1(mod23),且ad-bc≡0(mod23)},则集合A中元素的个数为____.
解析若a,d中有0, 由于a+d≡1(mod23),则(a,d)有(0,1)和(1,0)两种情况.此时ad=0,且ad-bc≡0(mod23),则b,c中有0,(b,c)有45种情况.所以,此类共有2×45=90种情况.
若a,d中无0,由于a+d≡1(mod23),则(a,d)有(2,22),(3,21),…,(22,2)共21种情况.
因为ad-bc≡0(mod23),注意到km(k,m∈{1,2,…,22})对每一个确定的k,km(m∈{1,2,…,22})的每两个值对于mod23不同余,即与1,2,…,22关于mod23同余的值各有一个,则km(k,m∈{1,2,…,22})的值与1,2,…,22关于mod23同余的各有22个.则对于每一个(a,d),(b,c)有22种情况.故此类共有21×22=462种情况.
所以, 集合A中元素的个数为90+462=552.
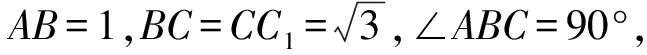


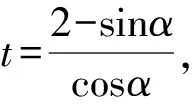



题7 如图1,将函数y=cosx+1(0≤x≤2π)的图象Γ画在矩形OABC内,将AB与OC重合围成一个圆柱,则曲线Γ在圆柱表面形成的曲线的离心率为____.
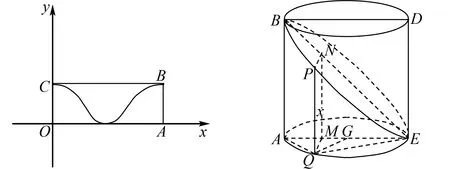
图1 函数y=cosx+1图象 图2 圆柱
解析如图2,设图1中OA,CB的中点分别为E,D,则围成圆柱后AE,BD分别为上、下底面的直径,易知AE=2. 设AE的中点为G,P为曲线上一点,作PQ⊥底面,垂足为点Q,QM⊥AE于点M,MN∥AB交BE于点N.


易知△NME为等腰直角三角形,则
所以PQ=NM,则四边形PQMN为矩形.
所以PN⊥NM,则PN⊥平面ABDE,于是点P在平面ABDE内的投影为点N.
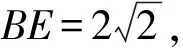
题8 设A,B,C是ΔABC的三个内角, 则3cosA+2cos2B+cos3C的取值范围为____.
解析设M=3cosA+2cos2B+cos3C.
易知M<6,当A→0,B→π,C→0时,M→6.
当C→0时,M=-3cos(B+C)+2cos2B+cos3C→-3cosB+2cos2B+1,

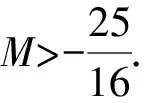

此时,A不是A,B,C中最小的.
(1)若C最小,则C 此时cosA+cosB-cosC+cos2C≥0,证明如下: cosA+cosB-cosC+cos2C =-cos(B+C)-cosC+cosB+cos2C 所以cosA+cosB-cosC+cos2C≥0成立. 所以3cosA+2cos2B+cos3C ≥3(-cosB+cosC-cos2C)+2cos2B+cos3C =-3cosB+2cos2B+3cosC-3cos2C+cos3C =4cos2B-3cosB+4cos3C-6cos2C+1 所以3cosA+2cos2B+cos3C≥cosA+cos3C=-cos(B+C)+cos3C >-cosC+cos3C=4cos3C-4cosC. 题9 已知抛物线Γ的顶点是原点O,焦点是F(0,1). 过直线y=-2上任意一点A作抛物线Γ的两条切线,切点分别为P,Q,求证: (1)直线PQ过定点;(2)∠PFQ=2∠PAQ. 证明(1)易得拋物线Γ的方程为x2=4y. 即x1x-2y-2y1=0. 同理,过点Q的抛物线Γ的切线l2的方程为x2x-2y-2y2=0. 由l1,l2过点A, 可得 x1t+4-2y1=0,x2t+4-2y2=0, 这表明,点P(x1,y1),Q(x2,y2)的坐标满足方程tx-2y+4=0. 所以直线PQ的方程为tx-2y+4=0. 所以易得直线PQ过定点(0,2). (2)不妨设点P在点Q的左边, 则x1 又因为 所以tan2∠PAQ=tan∠PFQ. 易知0°<∠PAQ<90°<∠PFQ<180°. 所以∠PFQ=2∠PAQ. 题10 给定正整数n(n≥2). 已知2n个正实数a1,a2,…,a2n,满足: 综上所述, 所求的最小值是n3. 解析先证以下 3 个引理: 证明由条件知f3=a+b. 假设n=k(k≥1) 时, 结论成立, 即 由归纳原理知, 对任意的正整数n,都有 回到原题: 注意到fn+1≥b, 且 (-1)nT=(-1)n(a2+ab-b2)≤b2, 所以2bfn+1-b2-(-1)nT≥2b2-b2-b2=0. 因此,Tn+1≥Tn对任意的正整数n均成立.