2023年高考数学北京卷平面解析几何解答题的多解、背景及推广
甘志国
(北京丰台二中,北京 100071)
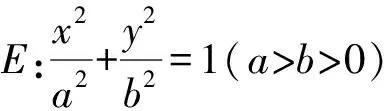
(1)求椭圆E的方程;
(2)若点P为椭圆E上位于第一象限的动点,直线PD与BC交于点M,直线PA与直线y=-2交于点N,求证:MN∥CD.


(2)先作出满足题意的图形如图1所示.
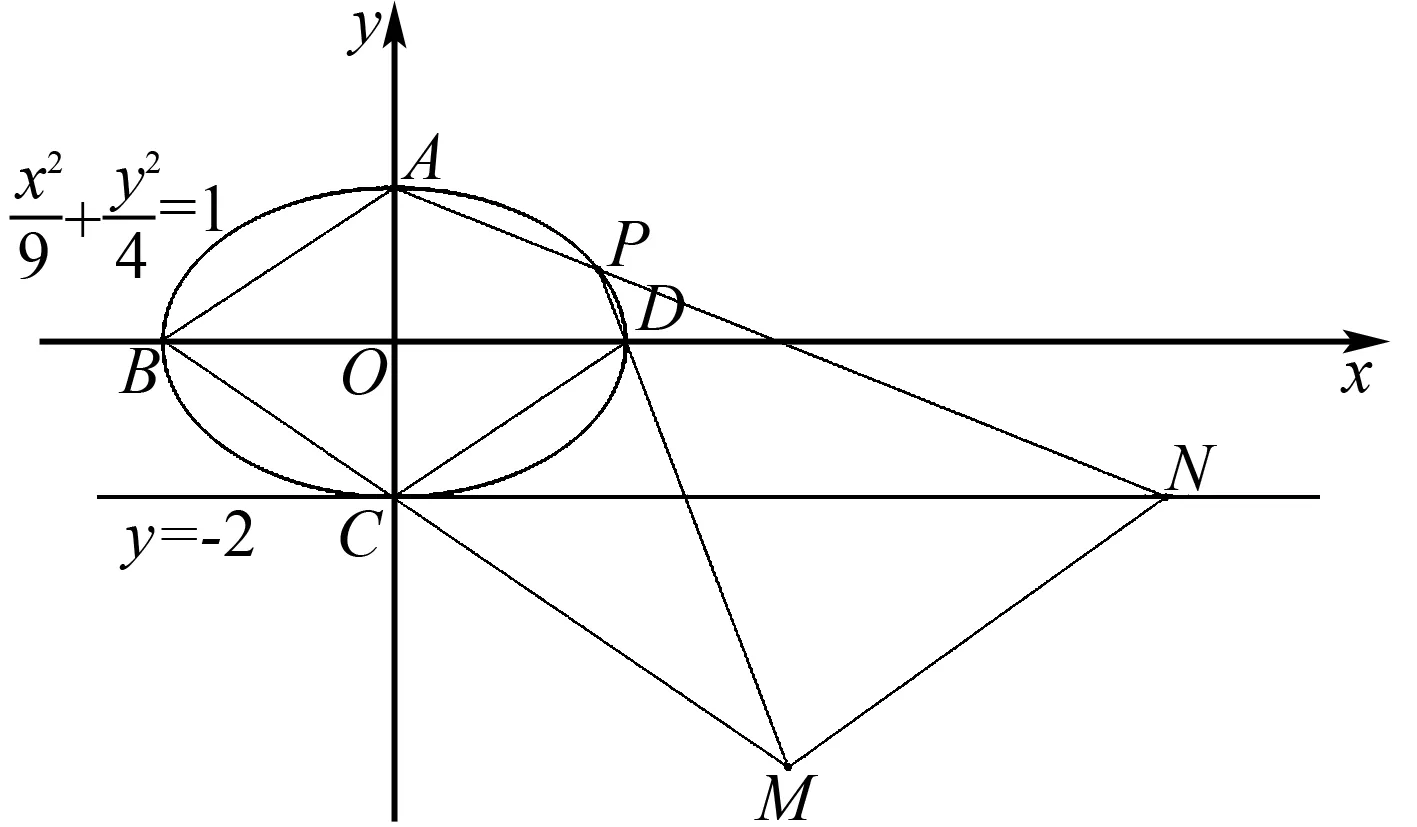
图1 2023年高考数学北京卷第19题
解法1 (设点并用椭圆的普通方程)可求得点A(0,2),B(-3,0),C(0,-2),D(3,0),再求得
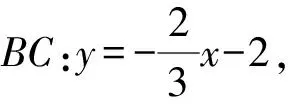
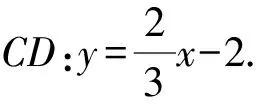
设点P(x0,y0),可得
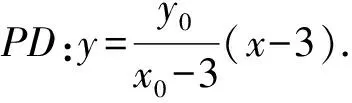
求得直线PD与BC的交点
直线PA与直线y=-2的交点
进而可求得直线MN的斜率
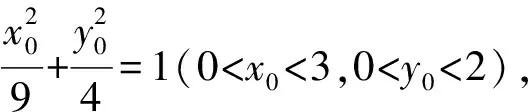
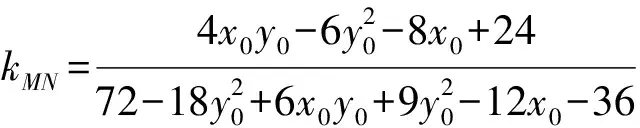
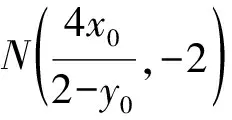
所以MN∥CD.
解法2 (设点并用椭圆的参数方程)可求得点A(0,2),B(-3,0),C(0,-2),D(3,0),再求得
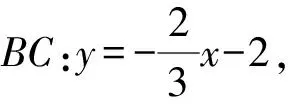
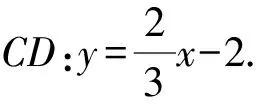
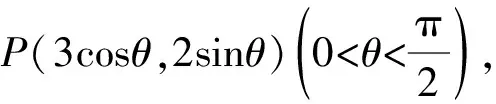

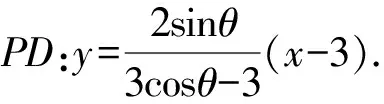
求得直线PD与BC的交点
直线PA与直线y=-2的交点
进而可求得直线MN的斜率
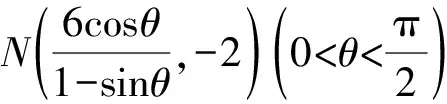
所以MN∥CD.
解法3 (常规方法设直线)可求得点A(0,2),B(-3,0),C(0,-2),D(3,0),再求得
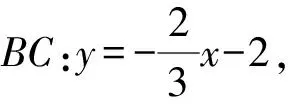
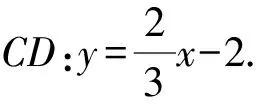
可设直线PD:y=k(x-3)(k<0),
进而可求得直线PD与BC的交点

(9k2+4)x2-54k2x+81k2-36=0.
由题设知,这个关于x的一元二次方程有两个不相等的实数根[1],且由韦达定理可得

进而可求得直线PA与直线y=-2的交点
再求得直线MN的斜率

所以MN∥CD.
解法4 (反设直线)可求得点A(0,2),B(-3,0),C(0,-2),D(3,0),再求得
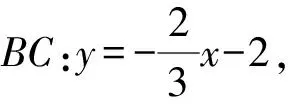
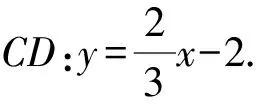
可设直线PD:x=my+3(m<0),
进而可求得直线PD与BC的交点

(4m2+9)y2+24my=0.

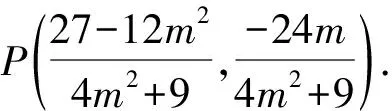

进而可求得直线PA与直线y=-2的交点
再求得直线MN的斜率

所以MN∥CD.
注这道高考题的背景是帕斯卡(BLAISE PASCAL,1623-1662)定理“二次曲线内接六边形(包括退化的情形)的三组对边的交点共线”[2].
如图1所示,椭圆E的退化内接六边形ABCCDP的三组对边AB与CD,BC与DP,CC(即直线y=-2)与AP的交点(无穷远点、M,N)共线,也即AB∥CD∥MN.
由此,还可给出该题的一般情形的结论:

由帕斯卡定理,读者可编拟出很多类似于本文开头高考题的题目.

