基于改进PSO-SA算法的城轨列车ATO节能优化研究

苏明健，肖宝弟，2，岳丽丽

（1.兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070；2.北京康吉森交通技术有限公司，北京 101318）

0 引 言

近几年，城市轨道交通以其运行效率高和方便快捷等特点受到各大城市的青睐，特别是随着列车自动驾驶（automatic train operation，ATO）技术的发展，研究列车节能性、准点性和舒适性等性能指标具有越来越重要的实际意义。列车运行优化的实质在于满足各性能指标的前提下，生成最优的目标速度—距离曲线，同时寻找一系列的组合工况和工况转换点，从而给出列车最优控制策略控制列车按照目标速度曲线自动运行。

在列车优化方面常用的智能算法主要是遗传算法（genetic algorithm，GA）、模拟退火（simulated annealing，SA）算法、粒子群优化（particle swarm optimization，PSO）算法、以及多种智能算法组合的混合算法等。大多文献基本都采用单一的智能优化算法，虽然对算法进行改进但并不能有效克服单一算法的局限性，不能达到较好的优化效果［1～6］。文献［7］将传统的PSO算法和改进的布谷鸟算法相结合形成的混合算法用在城轨列车的多目标优化中，优化所得结果明显体现出算法的优越性。文献［8］对速度建立多目标优化模型，充分考虑安全限制和轨道线路等多方面约束，采用差分进化和SA算法的混合进化算法对模型求解。但上述混合算法并未充分考虑优化过程中算法参数的变化，算法并不能在优化全过程中自适应变化。

本文将改进的PSO算法和SA算法相结合的一种自适应混合算法应用于城轨列车的多目标优化问题中。该混合算法综合了PSO算法实现简单，种群信息交换的优点，并结合SA算法搜索策略能够有效克服PSO算法优化过程中粒子易于陷入局部最优解的缺点，一定程度上有利于提高求取全局最优解的概率。同时对算法中惯性权重和学习因子等参数进行全局自适应性改进，进一步提高全局寻优的概率。结合实际线路条件和三阶段控车策略进行仿真实验，验证所提算法的可行性。

1 列车多目标优化模型的建立

1.1 列车动力学方程

本文采用单质点进行列车运动学建模。可以根据牛顿第二定律进行建模分析［9］。建立列车运动学方程

式中 M为列车质量；Ft为机车提供的牵引力或制动力；f为列车运行过程中的基本阻力，由经验公式得到；f0为列车运行过程中的附加阻力，随线路条件发生变化。

1.2 ATO多目标优化模型

城轨列车行车中的4 个性能指标进行综合协调，使列车的运行过程最大限度地满足4个综合性能指标。

1）舒适度模型

根据国际标准ISO2631—1 中的评价指标得知，影响乘车舒适度的是列车纵向加速度的变化率［1］，即所谓的“冲击率”。因此，本文对列车的加速度的导数进行建模

式中 Kj为列车运行过程中的“冲击率”，即“舒适度”的评价指标如表1；a为列车运行过程中的加速度。

表1 城轨列车舒适度评价指标

2）精确停车模型

为了安全考虑，地铁在站台与列车之间安装屏蔽门，这就使得城轨列车的进站停车距离需要保持在一定的范围内，才能使得乘客能够安全、正常的上下车［7］

式中 Ks为城轨列车精确停车指标；S为列车在相邻两站之间实际运行的距离；Sn相邻两站之间的距离，通常要求停车精度在30 cm之内。

3）准时性模型

本文采用列车实际运行时间和计划运行时间的差值对准时性进行建模［10］

式中 Kt为列车准时性指标；T 为列车实际运行时间；Tplan为列车计划运行时间。

4）能耗模型

本文在建立能耗模型时只考虑列车运行过程中列车牵引和制动所消耗的能源［11］

式中 Ke为列车能耗模型的衡量指标；Si为列车在第i 个工况下运行的距离，ai为车辆的加速度。

1.3 列车行车约束条件

1）安全约束

线路限速的约束：0≤v（x，t）≤vlim；起始点速度的约束：v（x0）＝v（xn）＝0。

2）工况约束

列车自动驾驶运行过程中常用的操纵工况有3 种：牵引、惰行和制动［10］。为了保证乘客乘车的舒适性，工况转换遵循原则如表2所示。

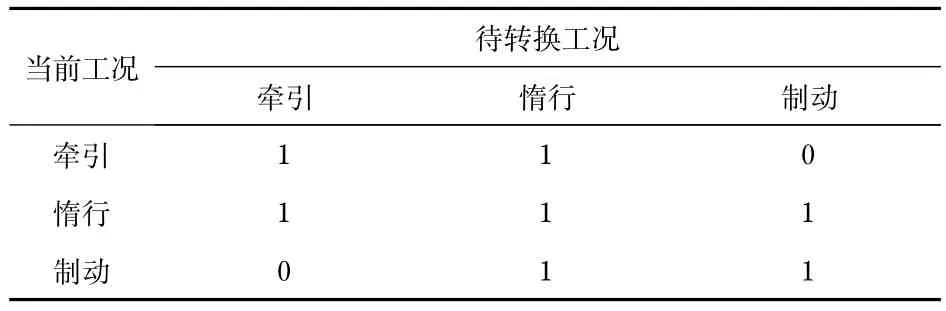
表2 工况转换原则

1.4 数学模型

多目标优化是在多目标之间达到一种相对最优。城轨列车的多目标优化数学模型表述为

本文通过权重系数，可以将复杂的多目标优化问题转化为单目标优化，从而有效降低求解的难度和复杂性。

2 城市轨道列车运行策略的分析

在实际行车过程中需要根据线路条件变化不断进行工况转换。

城轨ATO将多种运行工况进行合理组合。在现阶段列车运行过程中通常采用2 种运行策略：三阶运行策略“牵引—惰行—制动”如图1（a）所示；四阶运行策略为“牵引—巡航—惰行—制动”如图1（b）所示。

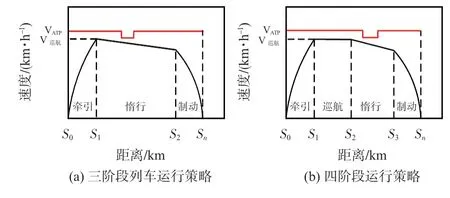
图1 三阶、四阶段列车运行策略

列车以不同的策略运行时，合力是不同的，当列车以不同的策略运行但在同一阶段运行时，合力是相同的［12］。

结合本文城市轨道交通列车仿真线路条件，由于线路区间行车距离较短、运行速度不高的特点，因此可以不考虑定速巡航工况。

3 自适应PSO-SA算法

3.1 PSO算法

PSO计算模型如下

式中 c1，c2为粒子的学习因子，分别为个体认知系数和群体认知系数；pbest，gbest分别为种群粒子个体引导者和全局引导者；xi（k），vi（k）分别为粒子第k时刻的速度和位置。

3.2 SA算法

SA算法［13］是一种基于Monte Carlo迭代思想的启发式寻优算法，在全局最优解的求取中具有较高的可靠性，也是局部搜索算法的拓展，能够有效克服其他优化过程中容易陷入局部最小值的缺陷和对初始值的依赖性。

3.3 改进的PSO-SA算法

本文利用SA算法搜索策略能够有效克服PSO算法优化过程中种群粒子易于陷入局部最优解的缺点，一定程度上有利于提高求取全局最优解的概率。

1）惯性权重自适应改进

惯性权重w在优化过程中控制当前粒子继承粒子的前状态的运动趋势，即粒子寻优搜索过程飞行的惯性。选取一种非线性的控制策略，即采用［-4，4］的双曲正切函数曲线来控制优化过程中惯性权重在种群优化过程中的变化［13］

式中 wmax，wmin为惯性权重系数取值的最大值和最小值，本文中取wmax＝0.95，wmin＝0.4；k 为当前优化的迭代次数，而kmax为优化过程中最大迭代次数，其基本函数图像如图2所示。可以看出，在寻优搜索前期，随着迭代次数的增加惯性权重变化速度相对较慢，这样会给予粒子足够多的时间进行全局范围搜索，有利于减少粒子陷入局部最优；搜索中期，变化速度较快，这样有利于进行局部的搜索；搜索后期，变化速度变得缓慢，可以进行更加精细的局部搜索，有助于搜寻全局最优解。

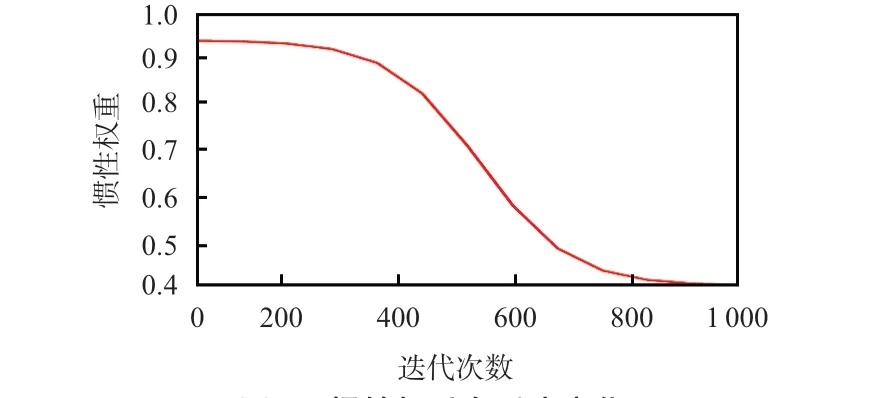
图2 惯性权重自适应变化

2）学习因子的改进

学习因子c1，c2分别起到调节种群粒子向个体最优和群体最优方向飞行的作用，当c1＞c2时，种群粒子会偏向个体最优，使种群粒子聚集在pbest等局部位置，影响全局寻优，反之则会偏向群体最优。根据闫群民等人［13］所提的算法优化策略，本文采取以下策略：随着迭代次数的增加，w不断减小，c1逐渐减小，c2逐渐增大

式中 c1max，c1min分别为个体学习因子取值的上、下限；c2max，c2min分别为群体学习因子取值的上、下限。这里取c1max＝2.5；c2max＝1.25；c1min＝1.25；c2min＝2.5。

3.4 算法优化的步骤

1）获取列车特性参数和线路基本参数，并设置初始w，c1和c2的值。设置搜索空间及搜索速度的边界值，设置种群大小的规模Size及最大迭代次数kmax；2）随机产生种群中所有粒子的初始位置和初始速度；3）根据公式计算粒子的适应度值并记录pbest和gbest，并设置模拟退火的初始温度；4）根据公式自适应的改变w，c1和c2；5）根据式（6）改变粒子速度，根据式（7）进行一次迭代寻优；6）计算移动后粒子的适应度；7）更新粒子的自身的历史最优位置；8）根据算法公式计算接受新解的概率pi（k）；9）以Metropolis 准则为依据，对比概率pi（k）与rand（）判断是否由产生的新解替代全局最优解进行退火操作，更新温度；10）判断是否达到最大迭代次数kmax，若未达到返回步骤（5）；11）输出当前最优粒子，即寻优结果，算法终止。

3.5 算法评价

由图3分析可知，本文所采用算法寻优结果以及收敛性［14］效果相比于PSO算法和PSO-SA 算法更显著。

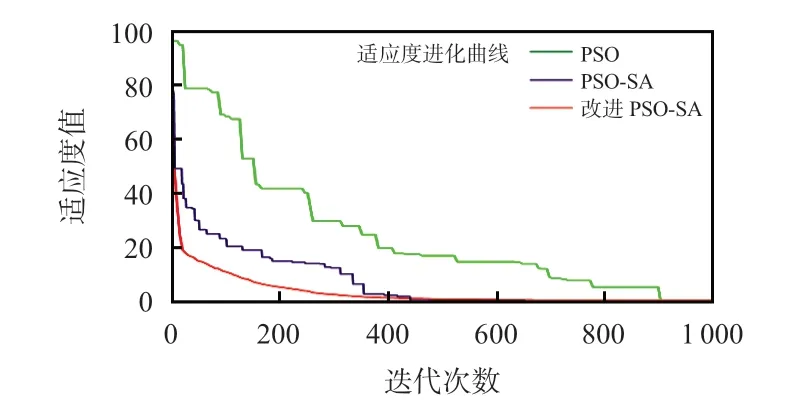
图3 算法进化曲线

4 仿真实验与分析

选取上海三号线（明珠线）轻轨的部分线路数据作为仿真的条件，采用阿尔斯通公司的03A01 型列车，利用软件进行仿真。仿真参数如表3、表4所示。

表3 仿真列车特性参数

表4 仿真线路参数

选择1 000m 线路作为仿真条件，站间运行时间90 s。通过改进的PSO-SA 算法对于控制序列的不断优化，经过1 000次的迭代取得优化结果，可以得出表5所示结果。

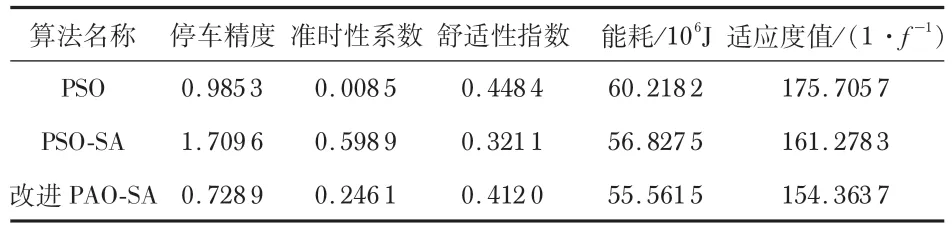
表5 仿真列车1 000 次迭代优化结果

1）安全性防护：经过算法的多次优化后，没有超速现象。2）停车准确度：基本稳定在30 cm，基本满足城轨安全要求。3）舒适度指标：从优化的结果看，达到乘坐舒适性的要求。冲击率越来越小，即乘客越来越舒适，且满足国际IOS2631的要求。4）能耗指标：经过1 000 次迭代次数的优化，可以看出能耗由60.218 2优化到55.561 5，节能率提升了7.7%。5）在满足线路车站限速、舒适性指标、停车精度和准时性的要求的前提下，能够将能耗有效降低7.7%，同时给出合适的工况转换点，能够为城轨列车运行提供有效的指导。

图4分别为3种算法对城轨列车多目标进行优化得到的加速度和速度—距离曲线，由图可以看出，经过改进PSOSA算法优化后得到的结果对比其他两种算法，工况转换较少，速度—距离曲线较为平缓，同时能够满足限速和乘客舒适度的要求。

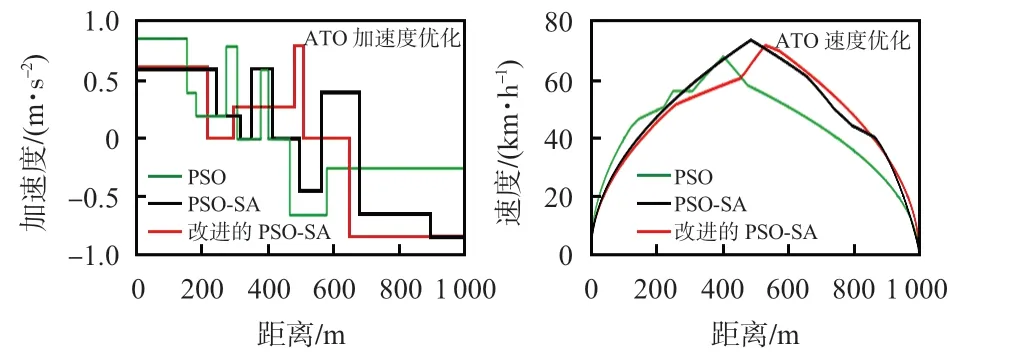
图4 3 种算法优化曲线

5 结 论

1）相比干线铁路线路，城轨列车线路环境较复杂，相邻车站之间的运行距离较短，并且站间存在多个坡道、弯道和隧道。单质点列车运行模型难以精确模拟列车的实际运行工况。因此，在以后的研究中应该考虑建立更加准确的多质点运动模型。

2）本文基于PSO-SA算法的列车节能操纵策略求解算法，并对PSO算法的核心参数进行自适应改进。由实例仿真计算结果可知，该方法在多种不同的线路上均可求得较优的列车牵引力实用系数序列解，具有良好的执行性和鲁棒性。