基于测地线流式核的隐空间多工况软测量建模*

任 超，叶泽甫，程 兰，乔铁柱，阎高伟

（1.太原理工大学 电气与动力工程学院，山西 太原 030024；2.山西格盟中美清洁能源研发中心有限公司，山西 太原 030000）

0 引 言

由于工业现场高温高压、强酸强碱、强干扰等恶劣环境，很难直接采用硬件传感器监测关键质量变量。基于数据驱动的软测量被研究应用于工业过程中难测参数的在线测量［1～3］。目前，应用领域较为广泛的数据驱动建模方法有以偏最小二乘（partial least square，PLS）回归为代表的回归分析 方 法［4］；高 斯 过 程 回 归［5，6］、支 持 向 量 机（support vector machine，SVM）［7，8］等基于统计学习发展起来的机器学习方法；以神经网络为代表的机器学习方法［9，10］等。但是，实际工业生产过程为了满足产品多样化的需求，具有多个稳定工况；同时原料和生产环境的改变也会导致工况发生漂移，产生新的运行工况。在新工况缺乏标记样本时，由于新工况过程数据和历史工况数据不再服从同样的概率分布，工况变化造成原有模型失配，对软测量带来不利影响。

迁移学习是指从数据标记量充足的源域中学习知识，将其迁移至数据标记量较少甚至没有标签的目标域，使得在目标域上取得良好的学习效果。文献［11］利用源域和目标域数据的全局协方差结构，将2 个域的数据分别投影到对应子空间，学习一种子空间对齐（subspace alignment，SA）的映射函数实现域适应。文献［12］提出一种联合分布适配（joint distribution adaptation，JDA）方法，将源域和目标域的边缘分布和条件分布进行适配，在源域有少量样本的情况下进行迭代，提高了分类器精度。文献［13］将测地线流式核引入过程监控，利用主成分分析（principal component analysis，PCA）获取2 个域各自的差异信息后，在流形空间下进行迁移学习，有效提高了故障诊断的准确率。

由于迁移学习放宽了数据同分布假设，当新工况缺乏标记样本无法建模时，利用无监督迁移学习，将历史工况数据与未标记的新工况数据映射到同一空间，使用映射后的历史工况数据建立模型，不需要从头开始训练模型，节约了时间成本。但利用测地线流式核（geodesic flow kernel，GFK）进行域适应时只关注了历史工况和新工况的过程数据信息，在过程数据分布差异较大但标签数据分布差异较小的多工况下建模表现良好，却忽略了历史工况的标签信息，导致在标签变量分布差异较大的多工况下模型会失准。

为提高模型在多工况过程下的适应性，本文首先通过GFK对新工况样本和已标记的历史工况样本的过程变量进行域适应，减小工况过程变量数据分布差异，利用历史工况的标签变量和域适应后的数据获取隐空间投影矩阵，对2个工况间迁移特征进行重构，最后利用支持向量回归（support vector regression，SVR）模型实现多工况参数软测量。

1 相关理论与算法

1.1 GFK

GFK［14］方法是指将2个域的子空间分别视为高维格拉斯曼流形空间上的两点，选择合适的子空间维度后，构建两点间测地线，并计算GFK，实现由源域投影变换至目标域的过程。

在多工况运行过程中，假设采集到的历史工况数据为XS，用二维矩阵形式表示为XS∈Rm×p，采集待测工况数据为XT，用二维矩阵表示为XT∈Rn×p，m 和n 分别为采集样本数，p为样本具有的相同特征数。工况迁移过程如下：

1）构建测地线

将历史工况样本XS当作源域，待测工况样本XT当作目标域，利用PCA获取两个域的子空间XS，XT。根据两点间的最短距离定义测地线函数ϕ（t），令ϕ（0）＝PS，ϕ（1）＝PT。两点间最短距离函数定义为

2）计算GFK

将历史工况样本迁移至待测工况，针对两工况下的样本点xi和xj，xi，xj∈R1×p，即表示测地线函数从ϕ（0）迁移至ϕ（1），GFK由两样本点在测地线函数上的无穷维投影的內积定义［14］

G作为半正定矩阵表述如下

式中 Λ为对角矩阵，Λ1i，Λ2i，Λ3i为对角元素，θi为PS和PT的主角。

1.2 基于PLS的隐空间特征提取

假设某一工况数据ZS有m个样本，建模变量有p个辅助过程变量｛z1，z2，…，zp｝和q个主导过程变量｛y1，y2，…，yq｝，z，y∈Rm×1，其中，辅助变量矩阵Z ＝［z1，z2，…，zp］，主导变量矩阵Y ＝［y1，y2，…，yq］。利用PLS思想可以提取出既能有效反映工况辅助过程变量信息又能很好地解释工况主导变量变化规律的潜在特征。根据PLS 原理最终获取p×r维投影矩阵W ＝［w1，w2，…，wr］，r 为隐变量个数，wr为矩阵EFr-1FEr-1特征值对应的特征向量。E 和F分别为提取主成分过程中对Z和Y的残差信息进行标准化处理的结果。

2 GFK迁移隐空间投影建模方法

SVM是由Vapnik 等人提出的一种可用于回归预测以及解决各种分类问题的机器学习方法，数学原理和公式推导详见文献［15］。SVR算法具备优异的全局优化性能，在维数较高且具备复杂非线性特点的数据回归预测应用中展现出了较好的泛化能力［16］。

对于多工况软测量建模，运用GFK迁移域时将历史工况作为源域，待测工况作为目标域。将迁移后的历史工况数据利用PLS获取投影矩阵W，利用W将域适应后的历史工况和待测工况数据同时投影至PLS 隐空间，最后利用SVR对PLS隐空间下的重构数据进行建模。本文提出GFK迁移隐空间投影（GFK latent space projection SVR，GFK-LSPSVR）建模方法，图1为所提建模方法示意。利用SVR建模流程具体如下：

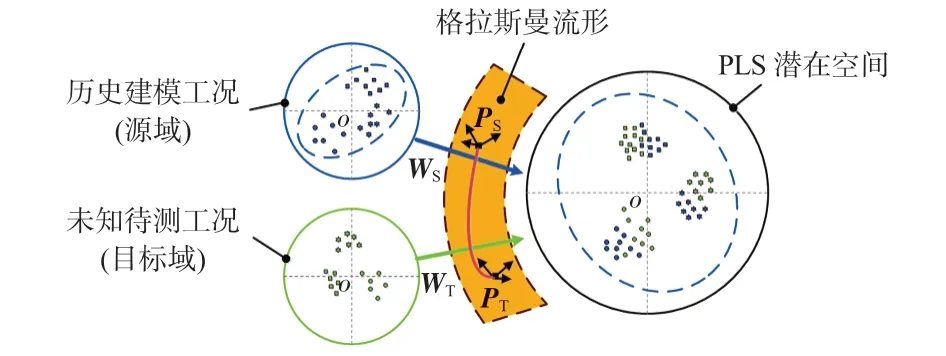
图1 GFK迁移隐空间投影算法示意

算法1GFK迁移隐空间投影建模流程

输入：历史工况a 建模样本Xa，历史工况a 数据标签Ya，待测工况b建模样本Xb。

输出：待测工况b数据标签Yb。

1）利用PCA将Xa、Xb投影到流形空间得Pa、Pb，根据式（1）构建测地线，并根据式（3）求得投影核G，进一步代入式（4）得到域适应后的数据Za、Zb；

2）利用PLS对域适应变换后的Za、Ya计算投影矩阵W；

3）根据W将Za映射到低维隐空间Ta＝ZaW，将Zb映射到同一低维隐空间Tb＝ZbW；

4）基于Ta，Ya建立SVR 预测模型，将Tb代入SVR 模型得到Yb。

3 TE过程仿真研究

3.1 TE仿真设置

本文采用TE 仿真实验平台进行多工况软测量实验。通过改变反应器压力和液位来模拟3 种不同工况条件，具体参数设置如表1 所示。选择15 个过程变量作为被监控变量［17］。对于每一种工况，分别采集1 000个样本。

表1 TE3 种工况参数设置

将3种工况中的其中一种工况作为历史数据集，预测另外2种工况下的反应物A，C浓度值。为说明本文GFKLSP-SVR方法的有效性，将其预测结果与SVR，GFK（GFKSVR）迁移回归以及常用于跨工况迁移软测量建模的联合分布适配（joint distribution adaptation SVR，JDA-SVR）迁移回归，子空间对齐（subspace alignment SVR，SA-SVR）迁移回归结果进行对比。本文实验采用均方根误差（root mean square error，RMSE）指标定量分析不同建模方法下的反应物浓度预测结果，如表2所示。

表2 各建模方法软测量均方根误差对比结果

图2分别给出了上述5种建模方法对不同工况下反应物A浓度的预测值，其中横轴n表示样本数。

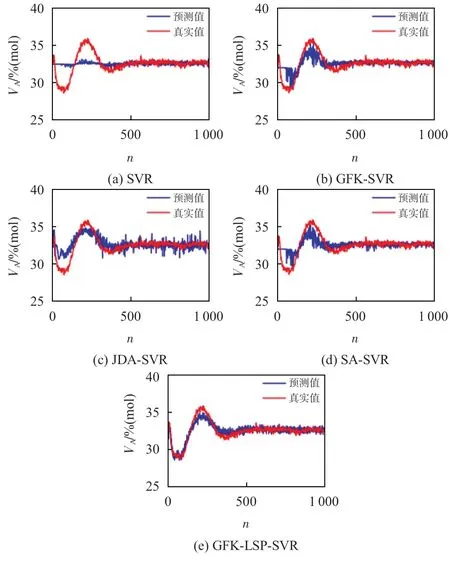
图2 工况二作为历史工况对工况一成分A浓度预测

3.2 实验结果与分析

结合表2和图2可知，针对非线性工况过程，基于SVR的软测量模型可以较好地预测稳定趋势下的工况标签。但当工况发生改变，尤其工况初期对预测工况前400 个样本进行标签估计时，过程变量的均值和方差随时间变化，其概率分布变化较为明显，SVR软测量模型失准；引入迁移学习策略后，JDA-SVR、SA-SVR 方法提取各工况间的方差信息进行域适应，通过适配或对齐工况分布差异信息来提取可迁移特征进行建模。GFK-SVR方法在流形空间下解决域迁移的问题，有效减小了工况过程变量数据分布差异，3 种方法都在一定程度上提高了软测量精度。本文所提GFKLSP-SVR方法在流形空间域适应基础上进一步利用工况标签分布信息重构隐空间特征，提高了建模特征对预测标签分布信息的表述能力，有效提升了软测量模型预测精度。主成分分析提取工况一和工况二样本的主成分，图3（a）～（c）分别表示两工况原始样本、迁移样本、隐空间迁移样本的前三维空间表述。由图中信息可知，两工况原始数据的空间分布差异较为明显；引入GFK 框架，在流形空间上充分考虑了工况样本高维非线性数据的结构特点进行域适应，减小了过程变量分布差异；隐空间投影进一步结合工况数据的差异信息和标签分布信息重构特征，数据分布更加趋于一致。

图3 数据经过域适应以及潜在空间投影的分布示意

4 结 论

针对由于工况数据分布差异而无法有效提升新工况下软测量模型精度问题，本文在引入GFK减小工况过程变量分布差异的基础上，利用已有工况的标签变量信息将域适应特征投影至隐空间后建模。TE 仿真软测量实验结果表明，隐空间下的重构特征更加充分利用了多工况数据分布信息，提高了建模精度。