基于改进蚁群算法的两栖无人飞行器陆空混合路径规划
尹秋石,姬书得,宋 崎
(1.沈阳航空航天大学航空宇航学院,沈阳 110136;2.沈阳航空航天大学自动化学院,沈阳 110136)
0 引言
近年来,人们对能够自主并能适应现代化农业、智慧医疗等领域的飞行器的需求越来越强烈[1],两栖无人飞行器因其有着能够跨越各种路况的能力逐渐出现在大众的视野中,占据着飞行器行业的主导地位。路径规划一直是飞行器领域的热门话题,也是自主导航的关键所在,其核心要求是按照特定的优化准则如距离最短、时间最短、能耗最低等搜索出一条从起始点到目标点的最优安全路径[2]。目前,国内外已经提出了很多用于路径规划的算法,如Dijstra 算法、A*算法、人工势场法等[3-5]。随着研究的深入,智能仿生算法及其改进算法逐渐突出,如遗传算法、神经网络算法、粒子群算法、蚁群算法等[6-9]。其中蚁群算法由于具有较强的适应性和鲁棒性,操作简单又易与其他方法结合,在路径规划领域得到了广泛应用。刘双双等提出一种新式多策略改进的蚁群算法以提高路径寻优性能和搜索效率[10],采用双层精英蚁策略加大最佳路径的信息素含量,提高了二维蚁群的寻优性;张文强等在蚁群算法中引入了具有人工势场思想的引力系数和避障系数[11],将路径的长度作为优化准则,得到了更优良的三维空间路径规划解;宋阿妮等针对三维无人机路径规划问题通过极值限定策略限定信息素浓度的范围[12],采用精英策略改进信息素浓度更新公式,提出了一种精英扩散蚁群优化算法;王晓燕等将蚁群算法与人工势场法结合给不同的栅格位置赋予不同的初始信息素[13],降低蚁群搜索的盲目性,提高算法在二维环境中的搜索效率;文献[14-15]分别将蚁群算法和遗传算法、粒子群算法相结合,提高了算法寻优能力,具有一定的灵活性。尽管上述文献已经用蚁群算法改进了飞行器及移动机器人的路径规划性能,但仅能对陆地或空中进行单一的路径规划,且对于算法的运行时间和迭代速度的优化研究还不够深入。对于两栖无人飞行器的路径规划而言,要充分发挥其多种行驶模式的优势,每一个飞行器所能携带的能源是有限的,要在有限的能源范围内使两栖无人飞行器行驶更多的路程完成更多的任务,规划出一条优质的陆空混合路径。
综合上述分析,本文以能源消耗作为优化标准,对蚁群算法进行了改进,使其运用在两栖无人飞行器的三维空间路径规划上,主要贡献归纳如下:1)在概率公式中引入前进角进行约束,使算法对于最优路径的搜索更具有方向性,使得全局搜索能力得到增强。2)改进信息素浓度更新规则,引入影响因子μ,加快了算法的迭代速度,减少了寻找最优路径的时间。3)创建一个以能源消耗为考量的评价函数进行适应度值的选择,最终生成一条陆空混合路径。
1 模型建立与问题分析
两栖无人飞行器是指既具备陆地快速行驶能力,又具备空中飞行能力,并可自由切换飞行、地面运动模式的一类飞行器,其作为一种新概念飞行器在国内外形成了研究热潮。
两栖无人飞行器用途十分广泛,可供商用也可供军用,尤其在应对紧急情况方面有着它独特的优势。譬如在消防、边境巡逻、救援和急件投递方面,两栖飞行器都有着非常适合的用处:在山地战争中情况多变,为节约能源,远距离输送时尽可能地进行陆地行驶,若遇山路受阻时便采用飞行行驶越过受阻路段,这时一种陆空混合路径规划便尤为重要,既稳定安全,又在保证物资按时送达的前提下节约了能源。
现假设在军事战争中某一山区由于突发状况导致部分山路受阻,无法通过陆地运输弹药物资,此时派出两栖无人飞行器为山区后的部队运送必要的用品。该地区是一个大小为a×b×c km3的空间(a=b=100,c=80),将山峰等障碍物简化为不同高度的单峰指数函数,如式(1)所示:
其中,n 表示山峰总个数,(xq,yq)代表第q 个山峰的中心坐标;hq为地形参数,控制高度;z(x,y)表示坐标为(x,y)时山体的高度值;xsq和ysq分别是第q个山峰沿x 轴和y 轴方向的衰减量,控制坡度。将三维空间按照高度进行切片,切片数量可以根据算法的精度要求和时间成本等综合考虑,针对每一个切片进行栅格化处理,如10×10 个栅格,栅格划分如图1 所示。
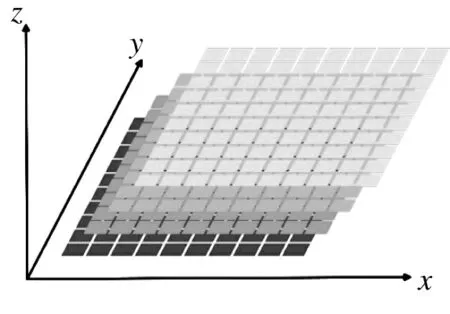
图1 栅格划分图Fig.1 Division of grid
两栖无人飞行器在陆地遇见无法逾越的山峰时选择飞行模式,在飞行过程中需要避开所有山峰,即两栖无人飞行器在点(xq,yq)上的飞行高度要大于山峰在该点的高度,否则会导致飞行器损伤或坠毁,公式如下所示:
其中,H(xp,yp)表示飞行器在点(xp,yp)时所处的高度,Sq表示第q 个山峰以(xq,yq)为中心在xy 平面上所有点的集合。
但在实际情况中,由于山峰坡度不同且飞行器有一定体积,当飞行器中心的飞行高度恰好高过山峰高度时仍然会发生碰撞。故将飞行器简化为一个长方体,其平面示意图如图2 所示。需留出足够的安全距离以保证任何时刻飞行器位置都不与山峰碰撞。
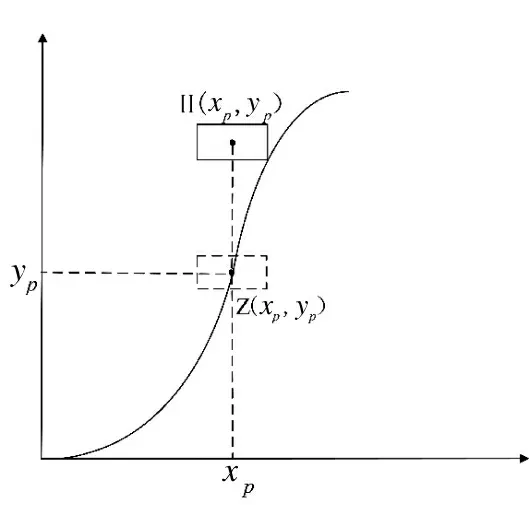
图2 无人机与山峰位置示意图Fig.2 The position of the drone and the peak of mountain
评价函数是用来评判飞行器路径优劣的方式,根据评价函数及三维地图,从起始点开始搜索,规划出可以到达目标点的陆空混合路径。即在满足约束条件的前提下,从栅格地图节点集合中选择路径节点,使两栖无人飞行器以较小的路径代价沿陆空混合路径节点运动,同时与障碍物保持安全距离。图3 为在三维空间中的理想陆空混合路径规划示意图,图中方块代表障碍物,实线代表在陆地时的行进,虚线代表在空中时的飞行,圆圈代表起始点,五角星代表目标点。
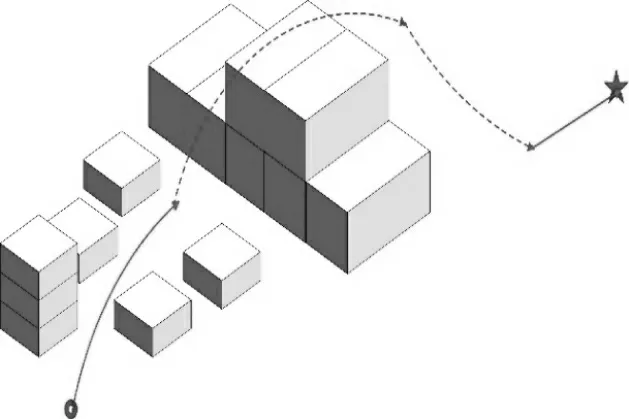
图3 理想陆空混合路径规划示意图Fig.3 Schematic diagram of ideal land-air hybrid path planning
2 改进蚁群算法的路径规划实现
2.1 基本蚁群算法原理
蚁群算法模拟了自然界中蚂蚁的觅食行为。蚂蚁在寻找食物源时,会在其经过的路径上释放一种信息素,并能够感知其他蚂蚁释放的信息素。信息素浓度的大小表示路径的远近,信息素浓度越高,表示对应的路径距离越短。通常蚂蚁会以较大的概率优先选择信息素浓度较高的路径,并释放一定量的信息素,以增强该条路径上的信息素浓度,这样,会形成一个正反馈。最终蚂蚁能够找到一条从巢穴到食物源的最佳路径,即距离最短。用蚂蚁的行走路径表示待优化问题的可行解,整个蚂蚁群体的所有路径构成待优化问题的解空间。路径较短的蚂蚁释放的信息素量较多,随着时间的推进,较短的路径上累积的信息素浓度逐渐增高,选择该路径的蚂蚁个数也愈来愈多。最终整个蚂蚁会在正反馈的作用下集中到最佳的路径上,此时对应的便是待优化问题的最优解。
蚂蚁l(l=1,2,…,m)在t 时刻从当前节点i 转移到下一个节点j 的转移概率,由路径上信息素浓度和距离启发函数确定,如式(3)所示:
其中,ij表示路径(i,j)信息素浓度,ηij是启发函数,表示蚂蚁从节点i 到节点j 的期望程度,如式(4)所示,allowedl为蚂蚁l 待访问节点的集合,α 为信息素启发因子,表示信息素浓度对转移概率影响;β 为期望启发因子,表示路径信息对转移概率的影响。
其中,dij是当前节点i 到待选节点j 的欧氏距离。在蚂蚁释放信息素的同时,各个节点间连接路径上的信息素逐渐消失,参数ρ(0<ρ<1)表示信息素的挥发程度。因此,当所有蚂蚁完成一次循环后,各个节点间连接路径上的信息素浓度需要进行实时更新,具体公式如下:
δij表示所有蚂蚁在节点i 与节点j 连接路径上释放的信息素浓度之和,δlij表示第l 只蚂蚁在节点i与节点j 连接路径上释放的信息素浓度,公式如下:
Q 为信息素强度常数,Dl表示蚂蚁l 在本轮循环中所走过的路径总长度。
2.2 改进蚁群算法
由于基本蚁群算法只能生成单一陆地行驶路径或单一飞行行驶路径,本文需注重能源消耗及路径长短生成一条陆空三维混合路径,考虑对概率公式以及评价函数进行改进;由于基本蚁群算法搜索最优路径的时间较长,考虑对节点方向性选择以及信息素更新规则进行改进。
2.2.1 概率公式的改进
蚂蚁l(l=1,2,…,m)根据各个节点间连接路径上的信息素浓度以及启发函数决定其下一个访问节点,引入影响因子μ,其计算公式如下:
其中,μ 为影响因子,是一个动态变量,随着每一代蚂蚁的更替进行变化,具体变化形式看式(9)。三维环境下dij的计算如式(8):
其中,x、y、z 为节点i 与节点j 沿x 轴、y 轴以及z 轴的坐标。
选取下一节点时,设定参数k,目的为选择下一节点调用不同参数 和η,当k=1 时为向上层走,k=2时为向平层走,k=3 时为向下层走。本文将信息素浓度 与启发函数η 分为3 类,如图4 所示。
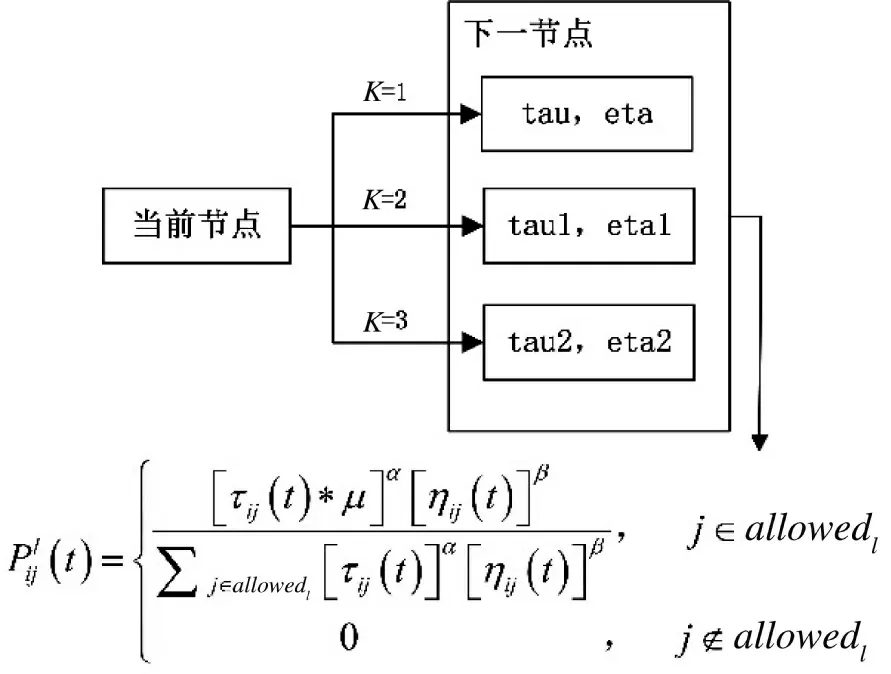
图4 选择调用参数Fig.4 Select call parameters
2.2.2 节点方向性选择的改进
在选取下一节点时考虑到方向性,期望蚂蚁向终点靠近,引入了前进角的概念,前进角代表当前点与下一节点连线同当前点与目标点连线在XOY平面的投影的两条线段所成的夹角。对前进角进行范围约束,使其不得大于θ/2,其中,θ 是以当前点与目标点连线在XOY 平面的投影的线段为角平分线向两边所能扩张的角度,蚂蚁只能在小于这一角度范围内前进,如图5 所示。传统蚁群算法在搜索过程中行走的随机性太强,收敛速度太慢,大大增加了算法的空间复杂度,前进角引入进行范围约束之后,使得算法初期搜索效率显著提高,无效蚂蚁路径显著降低。首先由当前点、目标点和下一节点向XOY 平面做投影,投影点分别为E、F、G,连接EF 使EF 为∠θ 的角平分线,连接EG。经多次∠θ 角度值的实验,发现当∠θ=90°时生成路径效果最好,大于90°时得到最优路径会耗时更多,小于90°时得到的路径并不十分优质,因此,本文算法将∠θ 的值设定为一个常值90°。蚂蚁在进行下一点的选择时,由于从起始点便已遵守夹角的准则,每选一个节点始终是向终点靠近的,故可忽视当前点的速度与下一选择点方向所形成的夹角较大的情况。
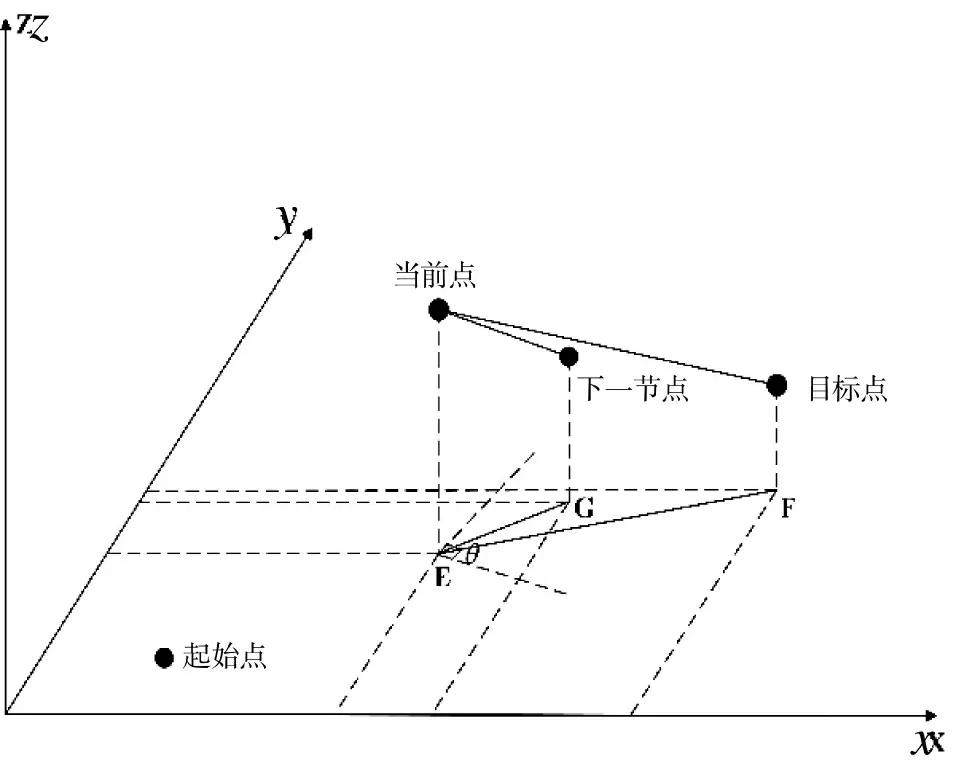
图5 夹角示意图Fig.5 Schematic diagram of included angle
2.2.3 信息素更新规则的改进
当一代蚁群完成一次路径搜索后,各个节点间连接路径上的信息素会逐渐消失,因此,需要对信息素浓度进行实时更新。为了更好地平衡全局寻优能力和局部寻优能力,加快算法的迭代速度与运算能力,本文引入影响因子μ,其作用为在计算第n 代蚂蚁信息素的更新时,不必从第一代一点点地计算,应用式(9)可直接计算出更新后的信息素。μ 的初始值设置为1,随着每一代蚂蚁的更替而变化,计算公式如下:
μn代表第n 代蚂蚁的值μ,参数ρ(0<ρ<1)表示信息素的挥发程度,改进的各个节点间连接路径上的信息素浓度实时更新的具体公式如下:
2.2.4 评价函数的改进
对于两栖无人飞行器陆空混合路径规划而言,评价函数是以能源消耗量设定的,消耗量值的大小会决定蚂蚁路径的选择。经查阅所知,一般两栖无人飞行器在飞行时额定电流是80 A,在行走时额定电流是8 A,当行进同等距离时,飞行所消耗的能源大约是行走所消耗能源的10 倍,由此评价函数公式如下:
其中,B 为每飞行1 m 所消耗的能源,C 为每行走1 m所消耗的能源。
2.3 改进蚁群算法的路径规划实现
改进蚁群算法的路径规划流程如图6 所示:
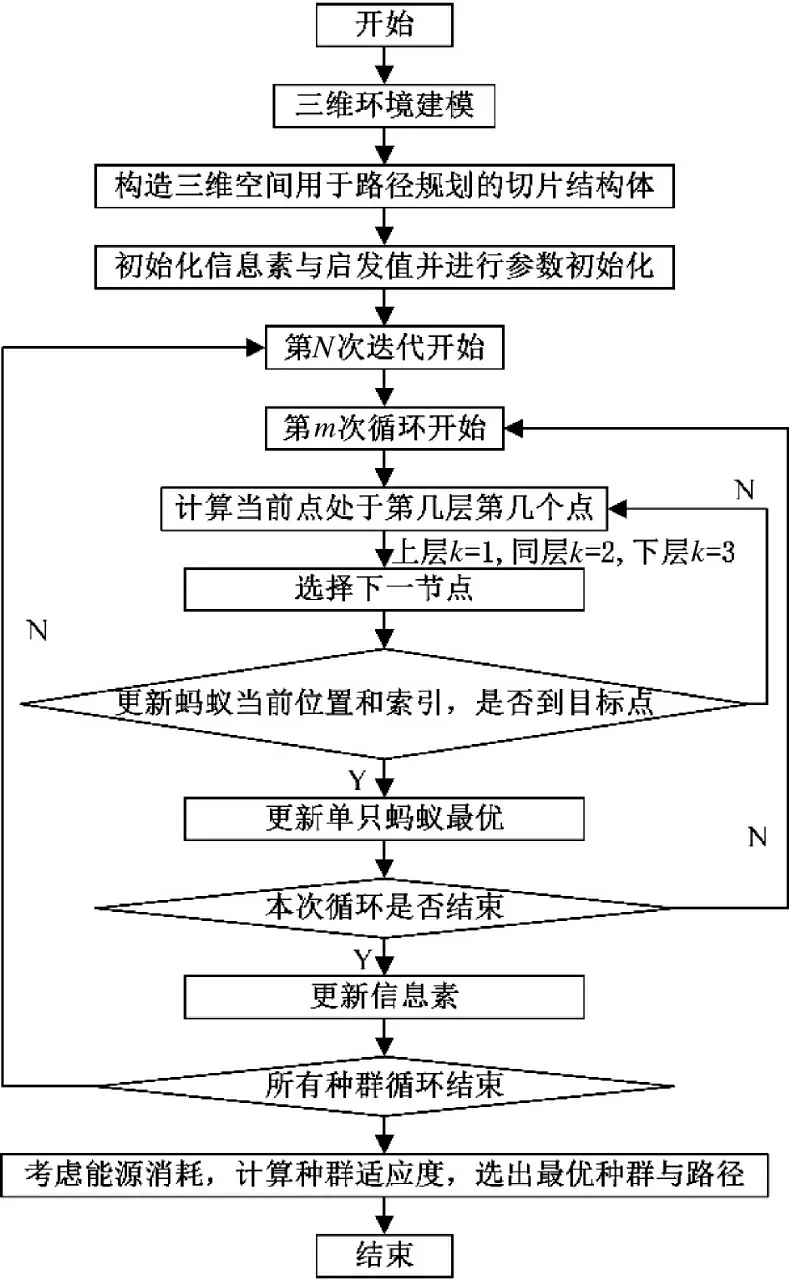
图6 改进蚁群算法流程图Fig.6 Flow chart of improved ant colony algorithm
具体步骤如下:
Step 1 已知静态三维空间进行三维环境建模,选择起始点与目标点。
Step 2 构造三维空间用于路径规划的切片结构体,将三维空间进行切片分层处理,结构体中包含每一层切片的允许访问栅格及每一层切片连接下一层切片的参数,参数包含信息素与启发值。
Step 3 初始化信息素和启发值及其他参数,设置蚂蚁数量m,信息素重要程度因子α,启发函数重要程度因子β,信息素挥发因子ρ,常数Q,最大迭代次数iter_max,影响因子μ,初始化每一代的最优蚂蚁。
Step 4 定义蚁群结构体,逐个蚂蚁进行路径选择,将起始位置和目标位置存放在蚁群结构体中,在选取下一节点时,考虑到飞行能源消耗大于行走能源消耗,尽量让飞行器在没有障碍的地方采用陆地行走模式。更新蚂蚁的当前位置和索引,判断其是否到达终点,若到达终点则更新单只蚂蚁的最优,判断本次循环是否结束,若结束则更新信息素直至所有种群循环结束。
Step 5 通过自定义的插值函数,根据每一个切片的栅格点,利用插值拟合得到三维路径,计算种群适应度值,选出最优种群与路径。
3 仿真结果与分析
通过MATLAB 软件对改进蚁群算法的路径规划方法进行仿真验证,作了两组具有代表性的实验,具体结果如下。
3.1 第1 组实验
规划空间为100 km×100 km×80 km,其中,x轴,y 轴方向每个节点间距1 km,z 轴方向每个节点间距5 km。设置路径起点在规划空间的坐标为(1,1,0),终点坐标为(96,96,0),各项参数值如表1所示。根据以下参数分别应用本文改进蚁群算法与文献[12]中的蚁群算法进行三维路径规划实验,仿真结果数据如表2 所示。
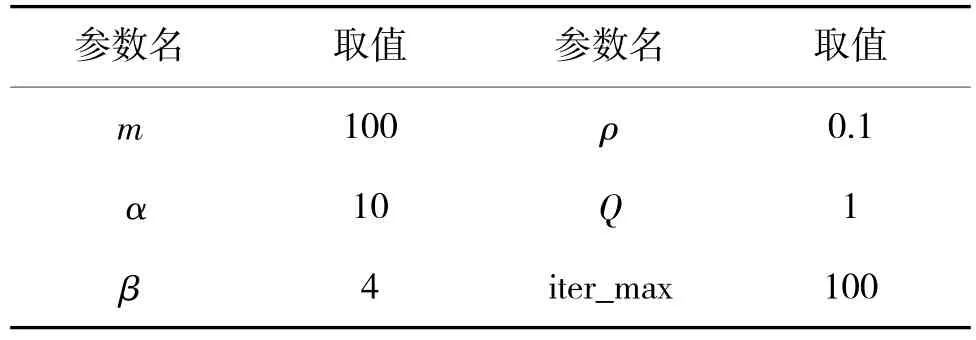
表1 实验参数取值Table 1 The value of experimental parameters
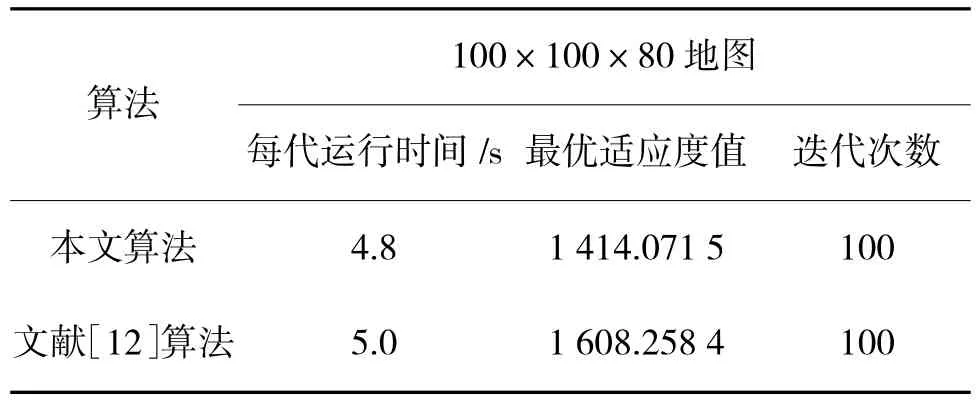
表2 运行结果对比Table 2 Comparison of running results
可以看出应用改进蚁群算法所得最优适应度值为1 414,较文献[12]的1 608 少了接近200 的能源消耗,这说明应用本文改进的蚁群算法比文献[12]消耗的能源更少,路径更优。之所以会有较少的能源消耗是因为应用本文改进蚁群算法生成了一条陆空混合路径,如图7 所示,而未考虑能源消耗的文献[12]仅能生成一条较短的无陆地模式的路径,如图8 所示。
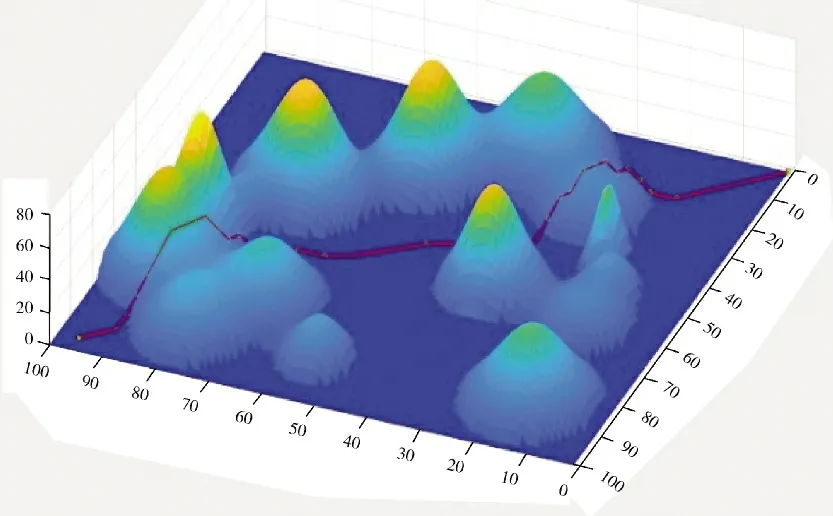
图7 本文算法生成路径Fig.7 The path generated by the proposed algorithm
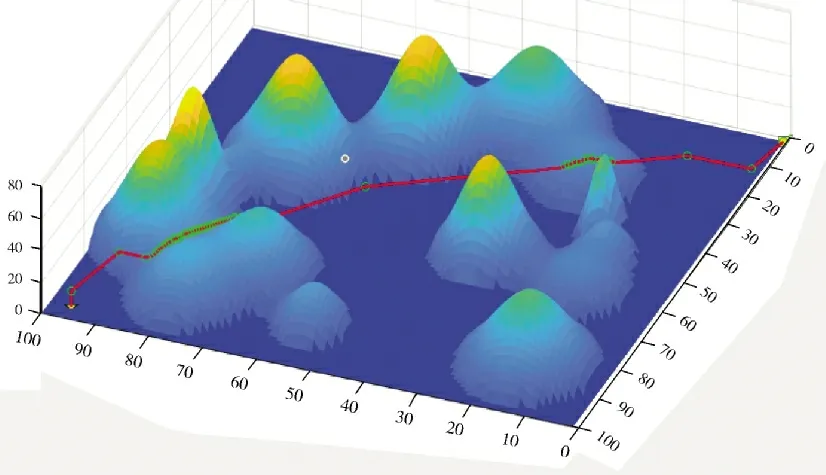
图8 文献[12]算法生成路径Fig.8 The path generated by the algorithm in reference[12]
3.2 第2 组实验
为验证影响因子μ 是否加快算法的收敛速度及减少算法的运行时间,规划空间为100 km×100 km×80 km,其中,x 轴、y 轴方向每个节点间距1 km,z 轴方向每个节点间距5 km。设置路径起点在规划空间的坐标为(1,1,0),终点坐标为(96,96,0)。根据表3的各项参数值,分别应用本文改进蚁群算法与基本三维蚁群算法进行三维路径规划实验,所消耗的时间对比图如图9 所示。
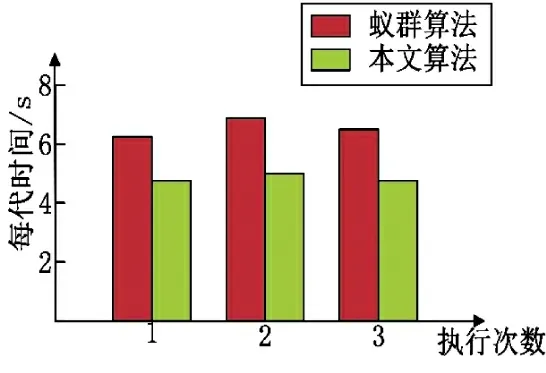
图9 改变终点后三维路径规划图Fig.9 3D path planning diagram after changing the end point
从图9 中可以看出,在生成的三维路径中本文改进蚁群算法比起基本三维蚁群算法运行时间更少,迭代速度更快。
4 结论
本文针对两栖无人飞行器在三维环境中如何由起始点到目标点合理地规划路径避开障碍物,并且尽可能地减少能源的消耗对蚁群算法进行了改进。在概率选点公式中引入前进角进行约束,优化了蚂蚁的搜索方向;引入影响因子μ 加快算法的收敛速度,减少算法的运行时间,优化全局信息素的更新方式;创建一个以能源消耗为考量的评价函数进行自适应度值的选择,最终生成陆空混合路径轨迹,使算法更具备实际意义。改进后的蚁群算法能够快速有效地实现两栖无人飞行器在三维空间中行走与飞行相结合的路径规划,相比基本三维蚁群算法只能飞行做出了创新,具有一定的优越性。不足之处是算法的运行时间相对较长,后续会对如何提高算法运行速度展开进一步研究。

