多级评分认知诊断题组模型*
周文杰 童望望 郭 磊,2**
(1.西南大学心理学部,重庆 400715;2.中国基础教育质量监测协同创新中心西南大学分中心,重庆 400715)
1 引 言
当前传统测验领域仅提供笼统的测验总分或学生能力值来衡量学生的学业水平,但随着对教育评估要求愈加精细,这种传统测验形式已不能满足人们对评估的需求。因此,心理教育研究者不断深入认知诊断测评(cognitive diagnostic assessment,CDA)研究,使其既可报告个体具有的认知结构或对知识的掌握情况,也便于教育者为学生进行更客观、更有针对性的教育评价,并为教育补救指明方向。
在各种大型测验中,如高考、TOEFL、PISA 等,常存在多个题目隶属于一个共同刺激的情况,如阅读理解、完形填空、选词填空等。这种一组题目共用一个刺激或材料的集合称为题组(testlet)(Wainer &Kiely,1987)。使用题组有较多优势:阅读材料能被充分利用,不仅节约作答时间提高作答效率,还能节约成本(DeMars,2012;Huang,2013);由于题目隶属于相同刺激,使得题目结构更复杂,相关性与逻辑性更强,就能测量被试更高层次思维能力(Haladyna,1992)。例如,图1 是一道考察“确定平面图中物体的位置的方法”(属性1)和“线段比例尺的应用”(属性2)的六年级数学综合题,该题目有两个小题,考生在作答过程中受到材料的共同刺激,因此这两个小题属于一个题组结构,题目(1)考察了属性1,满分为3 分,题目(2)考察了属性1和属性2,满分为4 分。这是一个典型的带有题组结构的多级计分题目。
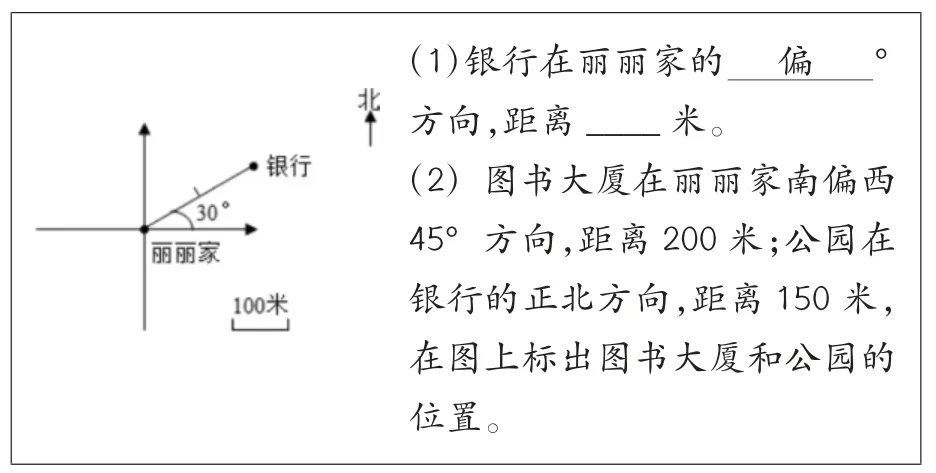
图1 六年级数学能力测试例题
在项目反应理论(item response theory,IRT)的领域中,研究者提出了多种处理题组结构的方式,其中具有代表性的方法有:(1)视同一个题组下的题目具有双重维度特性,一个维度是题组效应,一个维度是题目自身的效应,例如二阶模型(second-order mode)(Rijmen,2010) 和双因子模型(bi-factor model)(Demars,2006;Li et al.,2005);(2)将题目得分合成为题组得分,把同一个题组的题目看作一个多级评分题目(Wainer & Kiely,1987;Rosenbaum,1988);(3)将题组效应视为影响反应结果的潜变量,例如题组反应模型(testlet response models,TRM)(Bradlow et al.,1999)等。第一种处理方法具有较强的限制,仅能处理当题目只具有一层题组结构时的情况。第二种方法则会导致信息丢失,能得到题组得分,却不能获得被试精确的作答结果,且测验信度会被低估(Yen,1993)。第三种处理方法更灵活地表征了题组内的局部依赖性,获得更精确的参数估计结果,且具有较好的拓广性,可以处理多维题组的情况,是目前最常见的方式,本研究即采用该方法处理题组效应。
认知诊断领域中,詹沛达等人(2015)提出了能处理题组效应的认知诊断模型,后续结合反应时模型提出联合题组认知诊断模型(Zhan et al.,2018),Hansen(2013)结合2-tier 模型(Cai,2010)和LCDM 也提出了一种适用于认知诊断测验的题组模型。但这些模型只适用于二级评分数据,无法处理多级评分数据。而实际上,心理、教育及社会学等领域中存在大量多级评分题型,如简答题、材料分析题、Likert 量表等,尤其我国许多测验二级和多级评分题目经常混合使用(涂冬波等,2010),若采用二分模型拟合多级评分数据,会造成信息丢失(Ma&de la Torre,2016)。另外,虽然研究者已开发多种多级评分诊断模型,如Sequential GDINA 模型(Ma et al.,2016)、一般化多级评分认知诊断模型(General Polytomous Diagnosis Model,GPDM)(Chen & de la Torre,2018)、一般化分部评分认知诊断模型(General Partial Credit Diagnostic Model,GPCDM)(高旭亮等,2019)等,但是均不能处理题组效应。可以看出,目前能够处理题组数据的诊断模型不适用于多级评分数据,而已有的多级评分诊断模型不能处理题组效应,多级诊断模型与题组反应模型仍处于独立研究阶段。
综上所述,本研究拟将多级评分诊断与题组效应融合,开发多级评分认知诊断题组模型(Polytomous Cognitive Diagnosis Testlet Model,PCDTM)。本文首先介绍PCDTM 开发过程;其次介绍马尔可夫链蒙特卡洛算法(Markov chain Monte Carlo,MCMC)参数估计内容;第三,使用模拟研究探究模型参数返真性;第四,使用实证数据检验模型生态效度。最后总结研究结果,展望未来研究发展方向。
2 多级评分认知诊断题组模型的开发
2.1 多级评分认知诊断模型(GPCDM)简介
GPCDM 由高旭亮等(2019)提出,是一种以饱和模型GDINA 作为加工函数开发的多级评分认知诊断模型。GPCDM 用公式可描述为:
式中a1=(al1,al2,…,alk,…,alK)为被试属性掌握模式,l=1,…,L,L=2K。alk为属性掌握模式为a1的被试在第k 个属性掌握情况,若被试掌握第k 个属性,有alk=1,否则alk=0。qjx=(qjx1,qjx2,…,qjxk,…,qjxK)为第j 题第x 分属性考察情况,若考察了第k 个属性,则qjxk=1,否则qjxk=0。P(Xj=x)为属性掌握模式为a1的被试在第j 题得x 分的概率。λjx,k为alk主效应,λjx,k′k为alk′和alk的二阶交互效应;λjx,12,…,Kjx是掌握所有属性时对作答产生的效应大小。
2.2 多级评分认知诊断题组模型构建
2.2.1 多维题组效应
图2(a)表示单维题组效应,除被试能力θ 外,题目3 的作答还受到一个题组影响,且不同题组之间相互独立;而图2(b)多维题组测验中的题目3,4,5 同时受到了两个题组的影响(魏丹等,2017;詹沛达等,2015)。可见,单维题组是多维题组的特例。
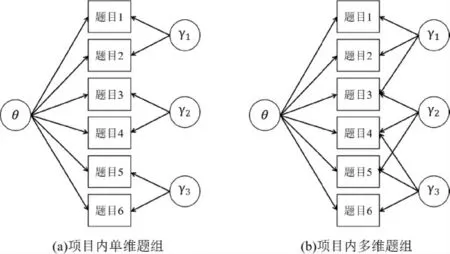
图2 单维/多维题组示意图
多维题组效应用公式可以描述为:
公式(2)表示被试i 在题目j 上共受到M 个题组效应的影响。协方差矩阵Σ 表示题组效应大小,Σ=(γi1,…,γim,…,γiM),γim~N(0,),γim表示被试i 在第m 个题组上的效应大小。用判定矩阵U 矩阵表示每个题目在不同题组上的归属,其中列表示题组,行表示题目,U=(Uj1,…,Ujm,…,UjM),Ujm表示题目j 是否归属于第m 个题组,属于则Ujm=1,否则Ujm=0。根据判定规则,图2(b)的题组效应可用图3 表示。
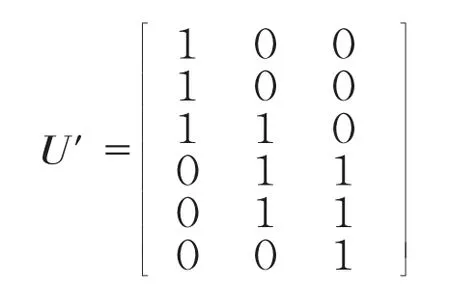
图3 U 矩阵示意图
2.2.2多级评分认知诊断题组模型(PCDTM)
进一步结合多维题组和多级评分结构,见图4(a)表示二级评分的多维题组结构,图4(b)表示多级计分的多维题组结构,mj表示第j 题的满分,可以发现在多级计分题组结构中,被试属性掌握模式α 影响所有的题目作答,同时题组效应γ 可以影响同一个题组中不同题目在不同得分的作答,从而进一步区别题组效应在不同得分水平的影响。为使多级评分认知诊断模型能有效处理题组效应,本研究在GPCDM基础上引入多维题组效应参数,得到了多级评分认知诊断题组模型(PCDTM),其函数表达式为:
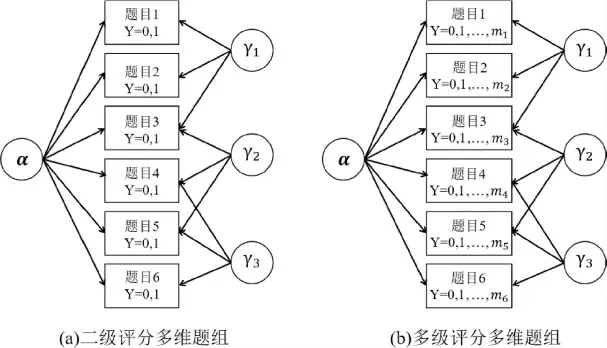
图4 二级/多级评分多维题组示意图
3 参数估计
研究采用R 语言R2jags 包,调用MCMC 算法进行参数估计,设定每种实验条件循环30 次,每次循环设定链数为3,每条链长5000,间隔数5,预热前2000 次,取后3000 次参数收敛结果平均数为该链参数估计结果。若所有被估计参数的小于1.1 或1.2,则参数基本收敛(Brooks&Gelman,1998)。参考Zhan 等(2019)设置,设定待估计参数的先验分布为:λjx0~N(-1.096,4),λjx,k~N(0,4)I(λjx,k>0),λjx,k′k~N(0,4),alk~Bernoulli(0.5),γim~N(0,),~invGam(1,1)。PCDTM 模型代码已上传https://doi.org/10.6084/m9.figshare.21581331,供读者参考和使用。
4 模拟研究
4.1 研究设计
模拟研究使用模型对比的方式,分别以PCDTM 和GPCDM 为真模型,生成有题组和无题组效应作答数据,再分别使用两个模型拟合数据。研究自变量包括:(1)真模型(GPCDM,PCDTM);(2) 样本量(500,1000,2000);(3)题目质量(高,低);(4)题目数量(20,40 题)。
4.2 类别Q 矩阵与U 矩阵设定
类别Q 矩阵(Category-Q,Cat-Q)和U矩阵间附表1 和附表2 所示(40 题Cat-Q矩阵与U 矩阵为20 题重复)。在Cat-Q 矩阵中,共考察了5 个属性,每个得分类别最多考察2 个属性,且每个属性考察次数相同。测验中第1~11 题为三级评分题目,第12~15 题为四级评分题目,第16~20 题为二级评分题目。测验包含四个题组结构,题组1 包含第1~11 题,题组2 包含12~15 题,题组3 包含16~20 题,3 个题组分别有部分题目包含于题组4,构成项目内多维题组结构。

表1 被试判准率PCCR/AACCR 值
4.3 模拟过程
4.3.1 被试参数设置
被试属性从伯努利分布中随机生成,即alk~Bernoulli(0.5),alk>0.5 取1,alk≤0.5则取0 从而得到不同属性掌握模式。
4.3.2 题目参数与题组效应设置
参考Ma 等人(2016) 和高旭亮等(2019)的生成方法,将高质量题目参数设置为:logit{gx[P(Xj=x | a1=0)]}从均匀分布U(0,0.25)中随机生成,logit{gx[P(Xj=x |a1=0)]}从均匀分布U(0.75,1)中随机生成;低质量题目参数设置为:logit{gx[P(Xj=x | a1=0)]}从均匀分布U(0,0.4)中随机生成,logit{gx[P(Xj=x | a1=0)]}从均匀分布U(0.6,1)中随机生成。
4 个题组效应满足多元正态分布,γ~MVN4(0,Σ),题组效应方差取值=0.25,=0.5,=0.75,=1(Wang & Wilson,2005),对角矩阵如下所示:
4.3.3 模拟作答
将被试及题目参数真值带入公式(1)和公式(3),计算被试在第j 题得x 分的作答概率P(Xj=x | a1),被试在该题最终作答结果根据对应概率大小进行抽取。
4.4 评价指标
使用均方根误差(root mean square error,RMSE) 和相对偏差的绝对值(the absolute of relative bias,ARB)作为题目参数和题组参数评价指标。平均属性判准率(average attribute correct classification rate,AACCR)考察属性返真性;属性模式判准率(pattern correct classification rate,PCCR)作为属性掌握模式返真性评价指标。以上指标是认知诊断研究中常见的参数估计精度的评价指标(詹沛达等,2015;Ma et al.,2016;Chen&de la Torre,2018)。
4.5 模拟研究结果
4.5.1 被试判准率返真性
表1 为被试判准率返真性。当真模型为GPCDM 时,PCDTM 与GPCDM 的判准精度非常相近,二者的PCCR 值最大差异仅为0.003,AACCR 最大差异为0.001。当真模型为PCDTM 时,PCDTM 明显优于GPCDM,二者PCCR 最大差异0.094,AACCR 最大差异0.021。这说明,当存在题组效应时,PCDTM 可以更准确地对被试进行判别。
当存在题组效应时,自变量中,题目质量的影响最大,样本量的影响最小。具体而言:①题目质量越高,被试判准率越高。在各题目质量条件下,PCDTM 判准精度均优于GPCDM,随着题目质量提高,使得两个模型判准精度均有较大提高,PCCR 最大可分别提高12.5%和12.3%。②随着题目数量增多,两个模型判准率均有所提高,但PCDTM 对题目数量变化更敏感,PCDTM的PCCR 最大可提升17%,GPCDM 最大仅为12.7%。在低质量条件下,随着题目数量的增加,两个模型判准率差距也随之增大,PCDTM 模式判准率大幅度提高,均维持在0.9 以上;而在高题目质量条件下,不论题目数量如何变化,PCDTM 始终有着较高判准率。③随着样本量增加,PCDTM 模型判准率也在稳步提升,PCCR 从[0.748,0.918]提高至[0.766,0.974]。
4.5.2 题目参数返真性
附表3 为题目参数返真性。整体上,当真模型为GPCDM 时,PCDTM 可以达到与GPCDM 相近的题目参数估计精度;而当真模型为PCDTM 时,GPCDM 参数估计精度要明显差于PCDTM。当GPCDM 为真模型时,两个模型题目参数估计精度大致相同。当PCDTM 为真模型时,GPCDM 的RMSE和ARB 整体增大,题目参数估计精度大幅度降低,而PCDTM 有较高的题目参数估计精度,且随着样本量、题目质量、题目数量的提高,估计精度进一步提高。其中,样本量影响最大,其次是题目质量,题目数量影响相对较小,GPCDM 题目参数返真性却出现混乱的情况。

表3 实证研究模型拟合结果
4.5.3 题组效应估计结果
图5 和图6 分别为PCDTM 为真模型时(即存在题组效应)和GPCDM 为真模型时(即不存在题组效应时)时,PCDTM 的题组效应参数返真性。整体上PCDTM 具有较小的估计偏差,随着样本量、题目数量的提高,对题组效应参数估计精度进一步提高,并且PCDTM 能较好识别没有题组效应的情境,结果表明PCDTM 模型在各种情境下均能较好地估计题组效应参数。
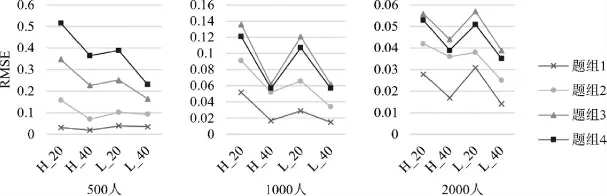
图5 PCDTM 为真模型时,PCDTM 的题组效应参数误差均方根(RMSE)
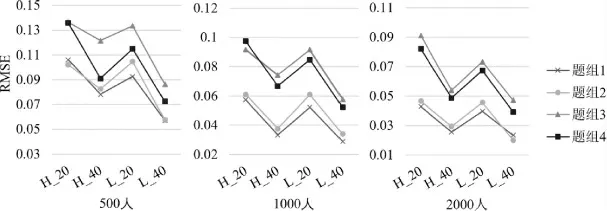
图6 GPCDM 为真模型时,PCDTM 的题组效应参数误差均方根(RMSE)
综上所述,当GPCDM 为真模型时,GPCDM 和PCDTM 判准率和题目参数估计精度差异较小;当PCDTM 为真模型时,PCDTM 判准率和题目参数估计精度明显优于GPCDM,且有较好的题组效应参数估计结果,而GPCDM 估计精度大幅度降低,且估计结果还出现混乱情况。因此,PCDTM诊断能力更佳,更具普适性。
5 实证研究
5.1 研究目的
分别使用PCDTM 与GPCDM 模型分析2012 年数学大规模测评数据,探查二者在实际数据应用中的效果。该测验为二级与多级评分题目混合,共114 题,考察了9476 名学生的三个数学认知属性:数与代数、空间几何与概率统计(魏丹等,2017),Cat-Q 矩阵见附表4。其中,测验有7 个题组,Testlet7 中5 个题目又分别属于其他5个题组中,形成项目内多维题组效应,加粗的题目即构成项目内多维题组效应(如表2 所示)。
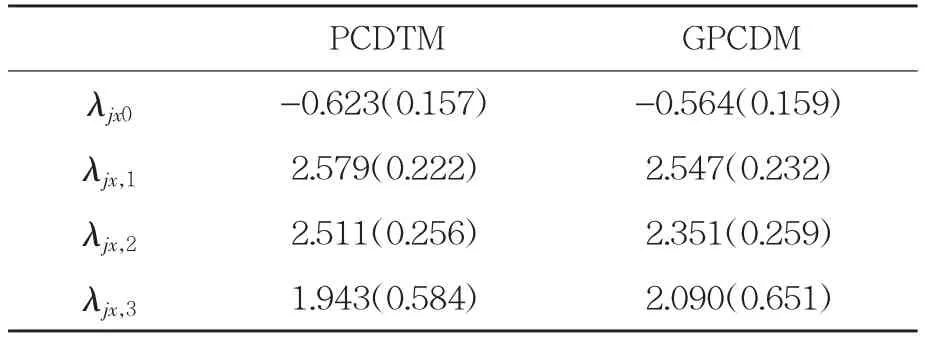
表4 题目参数估计均值(括号内为估计标准误)
5.2 评价指标
使用MCMC 参数估计中常用的偏差信息量准则(Deviance information criterion,DIC)拟合指标来评价模型在实证数据中的拟合效果。
5.3 研究结果
5.3.1 模型与测验整体拟合度比较
表3 为模型拟合结果。由结果可知,PCDTM 的拟合指标更小,数据拟合更优,表明在包含题组结构的测验中,更适合用PCDTM 进行分析。PCDTM 对七个题组效应方差的估计结果为=0.001,=0.507,=0.639,=0.397,=0.498,=0.846,=1.071。其中,第一个题组效应非常小,该题组可能不存在,其余6 个题组对该数学测验产生中等或高程度的题组效应。正是由于GPCDM 忽视了该测验的题组效应,导致模型拟合偏差增大。
5.3.2 题目参数估计均值比较
表4 为两个模型对实证研究题目的截距项和主效应项的参数估计均值及标准误。其中λjx0为截距项,λjx,1,λjx,2和λjx,3分别为三个属性的主效应参数。结果显示,相比于GPCDM,PCDTM 的题目参数估计的标准误更小,表明PCDTM 模型估计的可靠性更高。
整体而言,PCDTM 模型与实证数据的拟合情况更好,题目参数估计结果更佳,是处理带题组测验的优势模型。
6 研究结论与讨论
6.1 研究结论
本文将多维题组随机效应参数引入多级评分认知诊断模型中,成功构建了PCDTM 模型,并得出以下结论:
(1)PCDTM 合理有效,无论测验是否含有题组效应,均能得到精确的参数估计结果。随着样本量、题目质量、题目数量增加,被试判准率、题目参数与题组效应参数估计精度均有所提高。
(2)忽视题组效应,会降低题目参数估计精度和被试判准率,甚至出现估计结果混乱的情况。
(3)实证研究中,PCDTM 模型拟合更优,参数估计精度更高,是处理题组数据的优势模型,值得推广。
6.2 讨论与展望
6.2.1 PCDTM 适用性
整体而言,PCDTM 模型具有较好的参数估计表现,对无题组效应的作答数据也能达到与GPCDM 相近的精度,同时对有题组效应的作答数据,PCDTM 模型拟合效果更佳,参数估计精度也更高。这是因为PCDTM 模型对局部依赖性进行表征,将其视为影响作答结果的另一种影响因素,不仅能有效处理题目间存在的依赖性,还能减少了模型的系统误差,提高了模型对数据的拟合程度,从而提高对被试能力和题目参数估计的精确性。
6.2.2 PCDTM 使用建议
模拟研究中,题目质量对判准率影响最大,样本量影响最小;样本量对题目参数影响最大,其次是题目质量。当样本量增多,题目参数表现情况更好,若想得到较精准的参数估计结果,又保证运行效率,建议样本量不低于1000。高题目质量时,参数估计精度均较高,低题目质量时,即使样本量增加,判准率也较低,此时通过提高题目数量,参数估计精度便能大幅度提高。因此,在实际应用时样本量至少1000 人;题目质量较低时,题目至少40 题。
6.2.3 研究展望
未来研究可从以下方面探索:(1)本研究是以分部评分思想构建模型,未来可基于不同建模思想,构建丰富的多级评分题组模型;(2)项目功能差异检验(differential item function,DIF)是衡量测验公平性的重要指标,而目前基于题组模型的DIF 检验方法大多基于CTT 或IRT,也需要适合认知诊断的题组DIF 检验方法;(3)多项选择题(Multiple-Choice,MC)常以题组形式出现,虽已有对MC 题诊断方法的研究(Di-Bello et al.,2015;Liu&Liu,2021;郭磊,周文杰,2021),却未处理存在的题组效应,未来也需开发合适的诊断模型。

