智能移动终端室内异步声音定位方法

张磊,刘江,冯雪,屈秉男,何为,胡志新

(1. 长安大学工程机械学院,710064,西安; 2.西安现代控制技术研究所,710065,西安;3. 中国科学院上海微系统与信息技术研究所,201800,上海)

智能手机、智能手表、扫地机器人、无人服务系统等智能移动终端已经非常普及,特别是智能手机,以其完备的软硬件和低廉的价格成为了人们生活中的必需品[1]。高精度的位置信息,是智能移动终端实现各类应用的关键,也是未来智能系统发展与推广的基石[2]。基于北斗、GPS等系统的卫星定位技术,在室外场景推动了基于位置信息的服务(LBS)迅速发展。然而,复杂的室内环境极大地限制了卫星定位技术,室内LBS“最后一公里”问题仍未解决。

在过去的十多年里,学者们提出了许多基于蓝牙、WiFi、超宽带、惯性导航、地磁和超声波等技术的室内定位系统[3]。与其他技术相比,声音室内定位方法将消费级扬声器和麦克风作为测量元件,具有较高的测量精度和抗电磁干扰能力,且兼容绝大多数的智能移动终端,使其成为智能移动终端在复杂室内环境中实现高精度室内定位与导航最具竞争力的解决方案[4]。

声音室内定位系统的主要技术包括基于到达时间(TOA)、到达时间差(TDOA)、到达角度(DOA)[4]以及指纹匹配的定位方法[5]。基于DOA的定位架构需要传感器阵列[6],因此应用范围较小,系统兼容性较差。基于指纹匹配的定位系统,则需要建立指纹库,而建库和维护往往耗时且成本较高。基于TOA的定位系统需要预设3个基站(锚节点),通常具有更高的定位精度和稳定性,但要求基站与智能体间进行高精度的时钟同步[7]。基于TDOA的定位系统能够实现异步定位,即基站与智能体间无需进行时钟同步,但其需要预设4个基站,定位精度及稳定性弱于TOA架构[4]。尽管TOA定位架构具有诸多优点,但在实际应用场景中,高精度的时钟同步往往难以实现。

智能移动终端种类多样,所搭载的传感器类型、计算能力、通信模块、电池容量等具有较大差异,这就给智能终端与基站间的时钟同步带来了巨大挑战。作为智能移动终端最为常用的两类通信技术,蓝牙和WiFi仅能实现毫米级的时钟同步[8]。复杂多变的室内环境,使得时钟同步精度在实际应用中往往大于10 ms,距离估计误差大于3.4 m,进而严重限制了智能移动终端在室内的定位性能。一些基于LoRa或Zigbee同步技术的声音定位系统取得了亚米级的TOA定位精度[9],但通信技术的限制极大地降低了系统的兼容性。

基于TDOA的异步定位架构,可以规避时钟同步要求,但需要较高的基站部署密度。在实际应用中,增加基站部署密度,意味着系统应用成本的增加,会极大地限制技术的推广和应用。因此,需要在复杂的室内环境中,实现低基站部署密度的异步声音定位。

基于声技术自标定的空内智能手机追踪系统是较早出现的智能手机室内声音定位系统[8]。该系统的基站通过WiFi进行同步和通信,接收智能手机广播的18～22 kHz声信号,通过在8 m×8 m范围内布设的10个基站,基于TDOA定位原理实现了静态目标0.25 m的定位精度。其通过较高的基站部署密度来减轻WiFi同步精度所带来的影响。尽管WiFi的理论同步精度约为0.1 ms,但在实测中存在1～200 ms的浮动,这也给系统的定位性能带来了极大影响。

文献[10]系统通过迭代的方法剔除TDOA异常值,进而在15 m×15 m的场景内布设8个基站实现了静态目标0.2 m的定位精度,同时测试4个基站的定位精度为0.4 m。

Anthony Rowe 课题组于2018年提出了ALPS的增强版本[11]。该系统首先基于TDOA对低功耗蓝牙的同步偏差进行修正,再基于TOA实现了智能手机的室内声音定位,在实际场景中测试对静态目标的定位精度为1 m。

Cai等于2019年基于TDOA和声音多普勒信息,利用粒子滤波实现了智能手机的室内异步定位,通过在8 m×12 m的房间内布设4个基站,取得了移动目标0.49 m和静态目标0.12 m的精度[12]。

Chen等于2021年基于广义互相关和时频特征提取,提出了一种新的TDOA估计方法,进而结合扩展卡尔曼滤波融合智能手机惯性单元信息,通过在30 m×60 m的地下停车场布设8个基站,取得了0.5 m的手机定位精度[13]。该系统也是当前最接近实用的系统之一。

可以看出,现有方法的基站部署密度较高,能够获得较高的静态定位精度。动态定位场景的影响因素较多,使得精度和稳定性均较差。为了提高定位精度,往往需要引入滤波算法[14]。复杂多变的应用场景使得滤波算法合理的参数设置变得极其困难。

因此,本文面向智能移动终端的高精度室内定位需求,通过对声信号伪距和多普勒信息进行同时估计,基于距离差和相对速度量测,对短时位置序列中的多个位置进行联合估计,在低基站部署密度下实现智能移动终端高精度的室内异步声音定位。

本文所提出方法与现有方法的显著不同点在于:①基于声音伪距和多普勒信息获得距离差和相对运动速度量测,实现目标位置估计;②不再将不同时刻间的位置估计视作相互独立的过程,基于相对运动速度信息建立相邻时刻位置间的联系,将其转换为马尔科夫链,并对短时位置序列中的多个位置进行同时估计,以此来降低初始位置的误差传播和速度积分所引入的累积误差;③通过给初始位置以随机扰动,再基于迭代优化过程来提高整体位置估计精度;④仅需3个基站,即可实现高精度的异步声音定位。

1 多径传播对异步定位的影响分析

依据室内几何声学理论[15],室内声信道是一个衰落信道,受到墙壁及物体表面的反射,接收端所接收到的信号是声源通过多条路径传播的叠加。携带准确距离信息的第一路径信号成分淹没在了能量较强的多径叠加成分中。若所估计的信号时延为多径成分,则会为距离量测引入一个较大的正值,进而影响定位系统的精度和稳定性[16]。与无线信号相比,声信号在室内具有更强的多径传播效应,给基于距离的声音定位系统带来了巨大挑战。

在多径环境中,来自第i个和第j个基站的距离差表示为

(1)

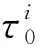
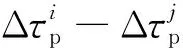
与时延估计相比,信号多普勒信息的估计不受多径传播效应的影响。因此,本文通过引入多普勒信息,融合TDOA与相对速度信息,来提高声音定位系统的定位精度和稳定性。

2 声音距离差及相对运动速度估计

对TDOA量测的估计,通常将来自不同基站的信号进行互相关操作来获取[18]。然而,室内较强的多径传播效应将模糊互相关结果的主瓣,进而降低TDOA量测估计的精度。因此,可首先估计智能移动终端到各基站的伪距,进而获得TDOA量测。

2.1 声音伪距测量

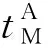
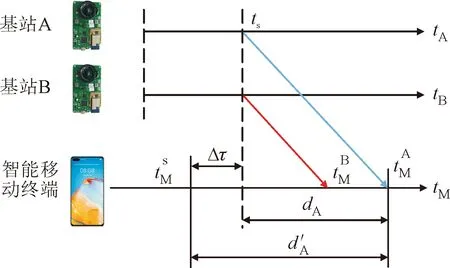
图1 声音异步伪距测量及距离差示意Fig.1 Asynchronous pseudorange measurement and TDOA

2.2 估计方法

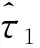
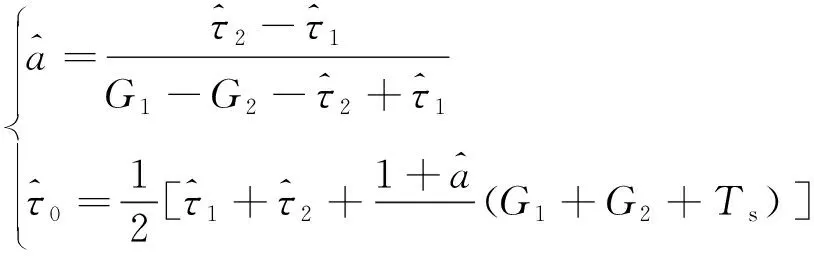
(2)

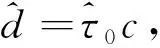
2.3 噪声分析

在室内场景,基站和智能移动终端的多径传播特性由两者的位置所决定。因此,在基于MF对文献[19]中的复合HFM信号中两个信号成分进行时延估计时,两者的多径传播影响可认为是相同的。因此可以假设两者均服从高斯分布,分别为

(3)

式中:τ1与τ2分别为两个信号成分第一径信号的时延真值;Δτp为多径信号的时延扩展。

(4)

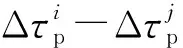
综上,通过复合HFM信号对伪距和多普勒信息同时估计,可以提高TDOA估计的稳定性,并获得较高精度的相对运动速度估计;进而通过融合距离差和相对运动速度信息,即可实现高精度的异步声音定位。

3 异步声音定位方法

3.1 数学模型

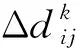
(5)

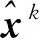
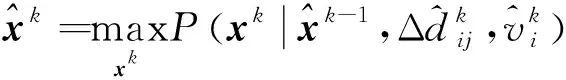
(6)

(7)

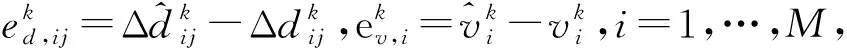
由式(6)可以看出,xk的估计精度受到xk-1估计结果的直接影响。同时,式(5)中的相对运动速度通过对时间积分来影响定位结果,这两个因素将无可避免地引起定位误差的累积。因此,可以通过对多个时刻的位置同时估计来减轻速度累积误差,通过改变初始位置的值来降低其对定位结果的影响。也就是,通过对一个短时位置序列中的多个位置同时估计,来提高定位精度和稳定性,并将此短时序列称为“短时位置序列帧”。选取要处理的位置序列帧长为T,该过程即对xk-T+1,…,xk-1,xk进行同时估计,表示为

(8)

相应地,最小二乘估计问题可以表示为[20]

(9)

其中拟合误差向量E表示为

(10)

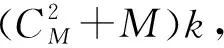
(2M-1)k≥Dk

(11)

进而可以获得最少基站条件

(12)

无论是D=2的二维定位场景,还是D=3的三维场景,所需的最低基站部署密度为2个。与现有异步定位常用的4个基站相比,所需基站数量少,定位精度更高。

对于式(9)的非线性最小二乘问题,基于泰勒展开的线性化方法将会引入较大的计算误差[21]。为了提高解的估计精度,常用最速下降法、高斯牛顿法以及LM(Levenberg-Marquardt)算法进行快速求解[22]。LM算法下降速度快,兼具高斯牛顿法局部收敛和最速下降法全局收敛的特点,是解决非线性最小二乘的有效工具[23]。因此,本文采用文献[24]所给出的LM实现方法,求解式(9)的高纬度非线性最小二乘问题。

3.2 方法框架

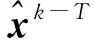
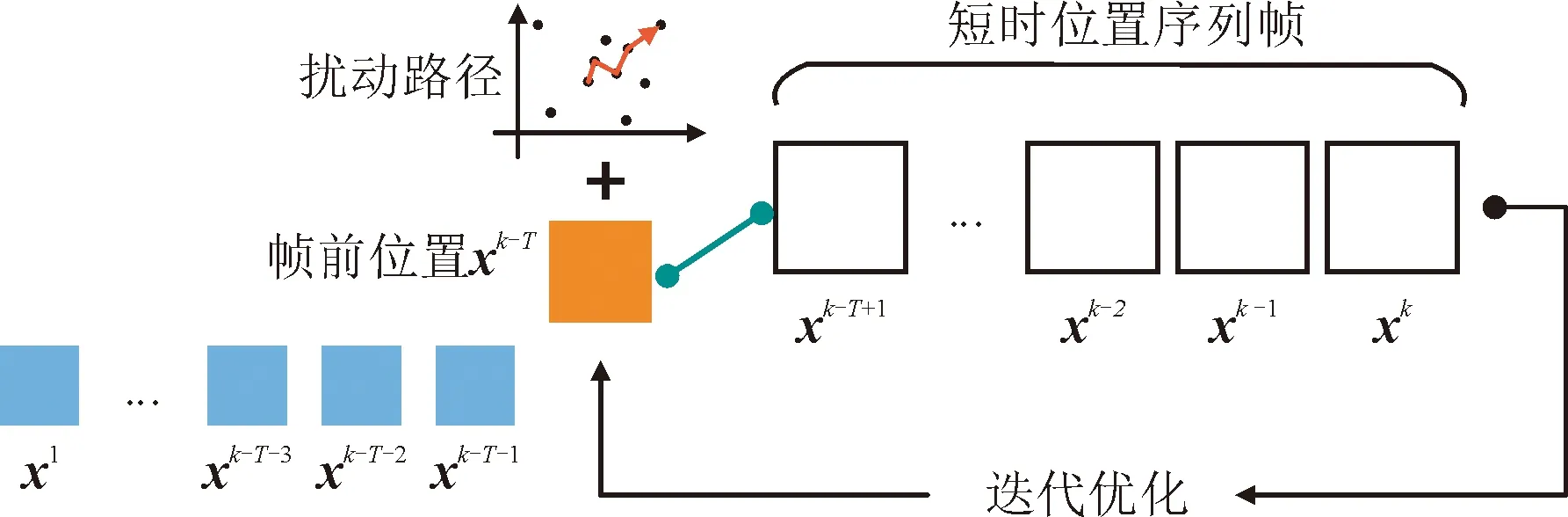
图2 本文方法定位流程框架图Fig.2 The framework of positioning procedure

短时位置序列帧长度T的选取,决定了拟合数据的长度,不仅会影响位置估计精度,也会影响整体计算复杂度。由于采用LM算法进行求解,其核心在于计算雅可比矩阵及海瑟尔矩阵。随着T的增加,两类矩阵的维度迅速增加,计算所需的内存和浮点数计算次数也急剧增加,进而增加了整体系统的功耗和成本,而位置估计精度也会得到改善。由于对目标的运动学模型进行了一阶假设,过大的T反而会削弱位置估计精度,因此需要选择合理的序列帧长度。

(13)

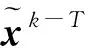
(14)

(15)

式中:a2为回退步长,且a2≤a1。

3.3 计算过程

在定位空间中布设M个基站,并确保定位空间内的每个待定位点均被覆盖。选定短时位置序列帧长度T,设定更新步长a1、回退步长a2、最大迭代次数nmax和最小拟合误差阈值ε。在第k时刻,估算xk-T+1,…,xk的步骤如下。

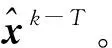
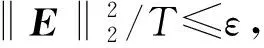
4 数值仿真与结果分析

本文以二维场景定位进行仿真,在20 m×20 m的场景内布设3个基站,如图3所示。基站位置为:[20,0],[20,20]和[0,20] m。携带智能移动终端的目标在场景内从位置[3,3] m,经[3,16]、[10,16] m和[15,10] m运动至[16,3] m。目标的运动速度分量取值为vx,vy∈{0,1}。设定序列帧长T=2,迭代次数nmax=20,阈值ε=0.15,更新步长a1=0.3,回退步长a2=0.1,初值扰动标准差σr=0.02。噪声cσ=0.2,声速设定为c=340 m/s。

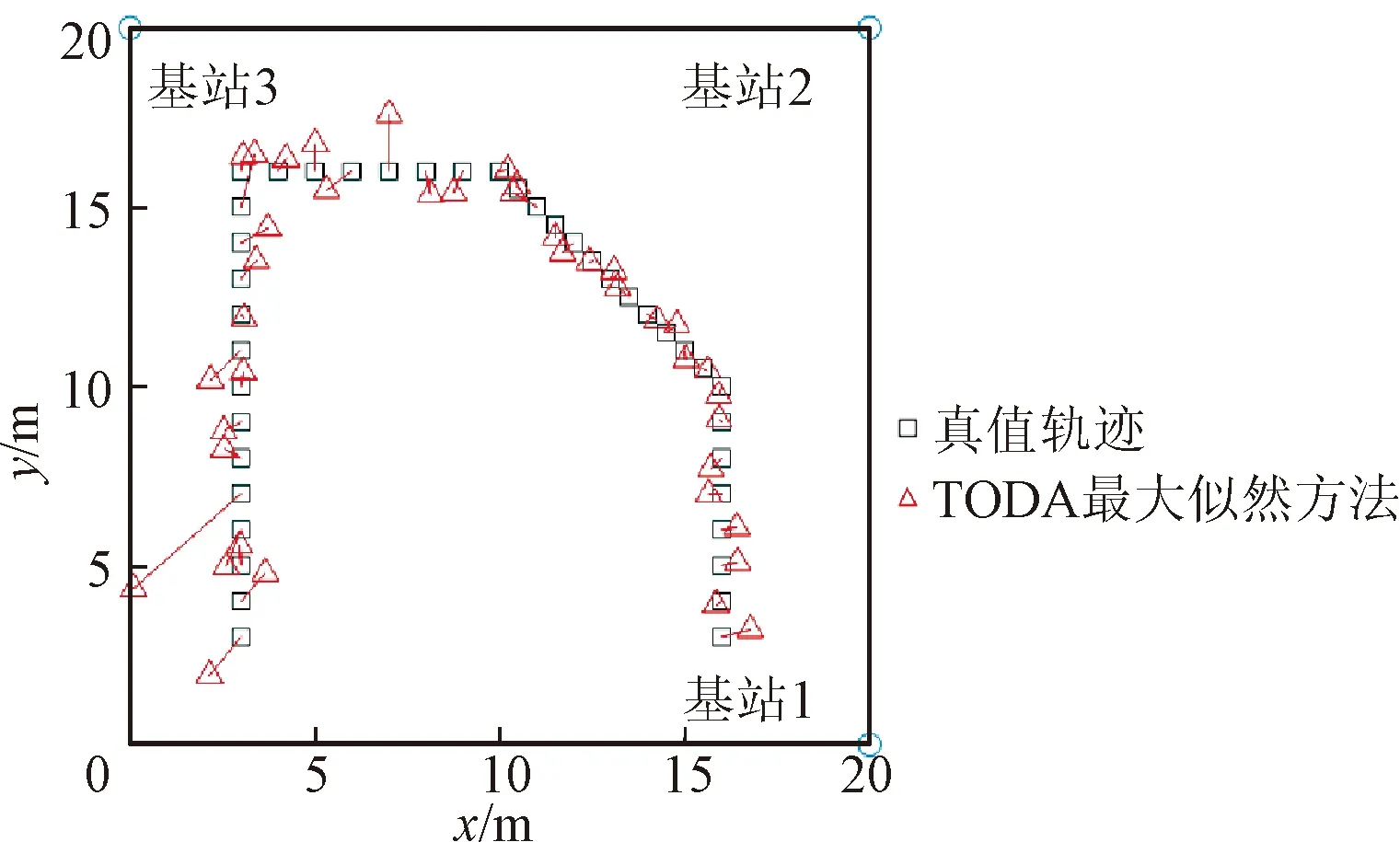
(a)TDOA方法

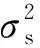
如图3所示为基于TDOA最大似然方法与本文方法结果的对比。基于最大似然估计的方法在理论上能够达到克拉美罗下界[25]。从结果可以看出,本文方法的定位结果稳定性更好,且精度更高。

为降低由于基站布局对定位结果的影响,在场景内增加[0,0]位置基站,并从4个基站中遍历3个基站的位置组合,每个组合重复仿真1 000次,统计其定位误差如图4所示。通过对比两类结果定位误差的累计分布函数(CDF, cumulative distribution function)可以看出,本文方法能够在多径环境中,获得更高的异步定位精度,定位误差小于0.5 m的概率为90%,小于0.28 m的概率为60%。

图4 定位误差累积分布函数对比Fig.4 The comparison of positioning errors’ CDF

4.1 短时位置序列帧长选择

序列帧长T会直接影响到定位精度和系统功耗。在各项误差设定及参数不变的情况下,通过在[2,15]区间内设定T的值,并遍历3个基站的不同组合,重复实验1 000次,统计90%置信度的定位精度,以及单次定位平均计算耗时,评估T对精度和计算耗时的影响,结果如图5所示。

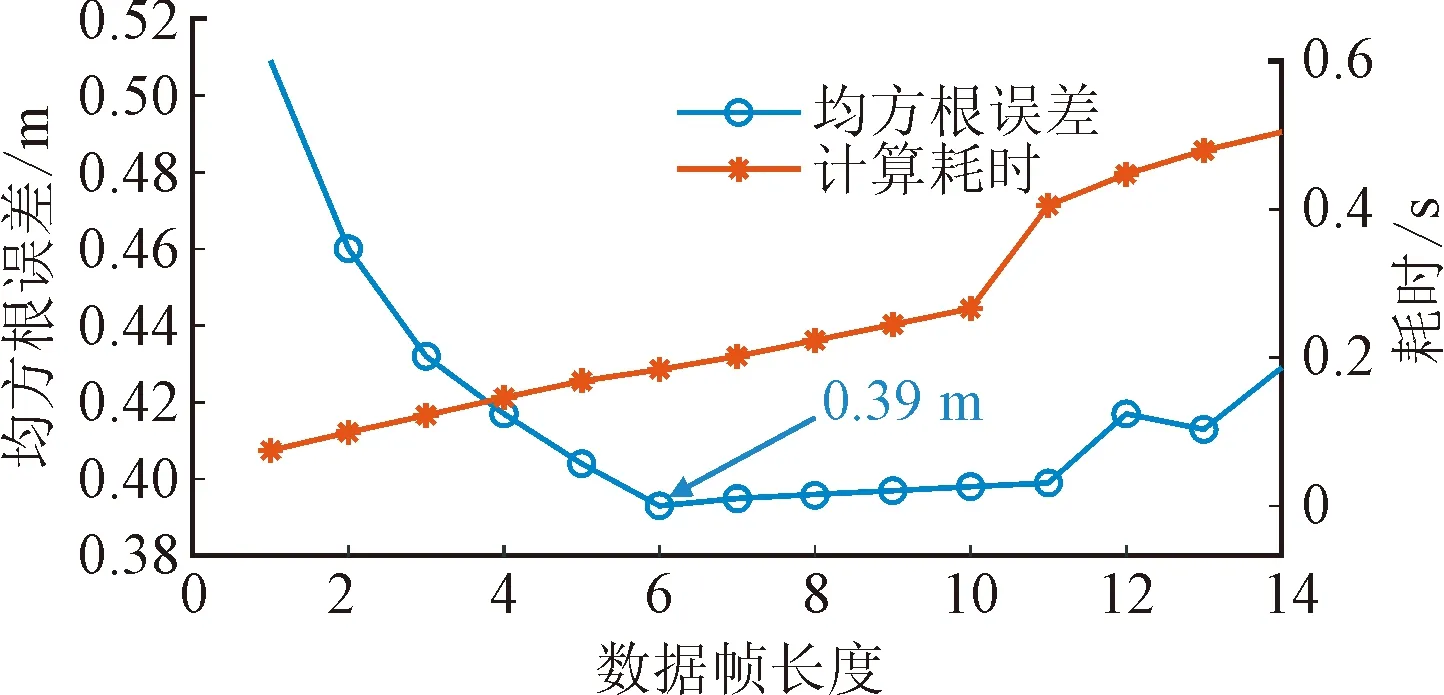
图5 序列帧长度对定位误差及计算耗时的影响Fig.5 The influence of T to the positioning error and computation consumption

从图5中可以看出,随着T的增加,位置估计精度会得到改善,而过大的T反而会削弱位置估计精度。这是由于,对目标的运动学模型进行了一阶假设,较大序列帧长度会涵盖目标更多的机动运动,从而增大了模型偏差。针对如图3所示的运动场景,当T=6时,系统具有最高定位精度,定位误差小于0.39 m的概率为90%。当T=4时能够兼顾精度与计算复杂度。

随着T的增加,雅可比矩阵及海瑟尔矩阵的维度迅速增加,计算量及所需内存均急剧增加,进而增大了单次定位的计算耗时。因此,计算耗时随着T的增加而增加,并呈现近似线性的关系。基于Matlab 2020b在CPU为i7-8700、内存为8G的PC主机上进行运算,在当T=2时,单次定位的计算耗时均值为74 ms。降低最大迭代次数nmax同样可以降低计算耗时,在nmax=1时的计算耗时均值约为4.8 ms。

4.2 噪声对定位结果的影响

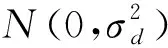
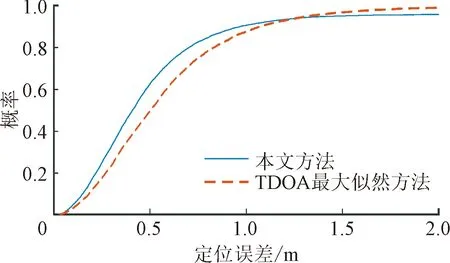
图6 无多径效应条件下σv=σd=0.4时的定位性能对比Fig.6 The comparison of positioning performance under no multipath effect with σv=σd=0.4

当标准差为0.4时,量测误差有85%的概率落在±0.57 m/s以内。相较于30 m的声基站覆盖范围,该误差噪声处在较低水平。目标移动速度通常为1 m/s,±0.57 m/s的噪声则意味着严重的噪声污染,会给系统定位带来严重的影响。即便如此,本文方法的性能仍然优于和接近TDOA最大似然估计方法。经统计发现,当σv和σd小于0.4时,所提出方法性能优于TDOA最大似然估计方法。也即是,在大多数的无多径效应理想条件下,本文方法能够有效提高异步定位的精度和稳定性。

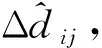
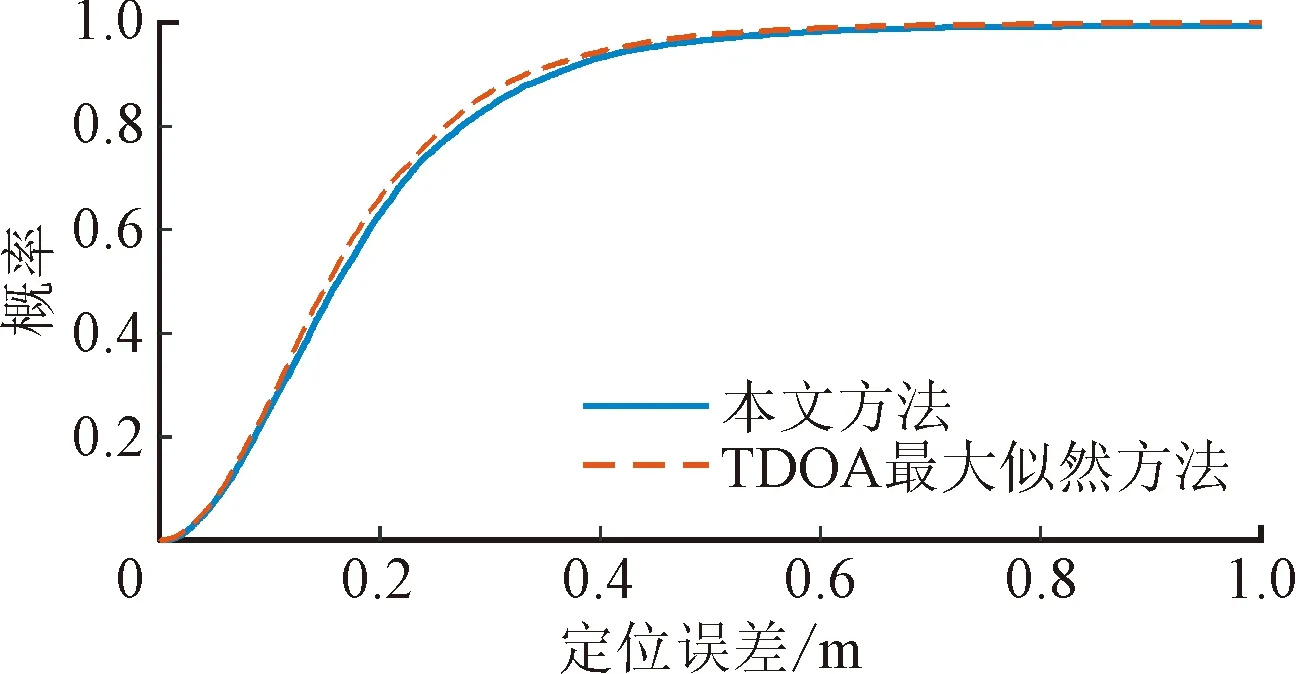
图7 多径噪声条件下的定位性能对比Fig.7 The comparison of positioning performance under multipath effect with

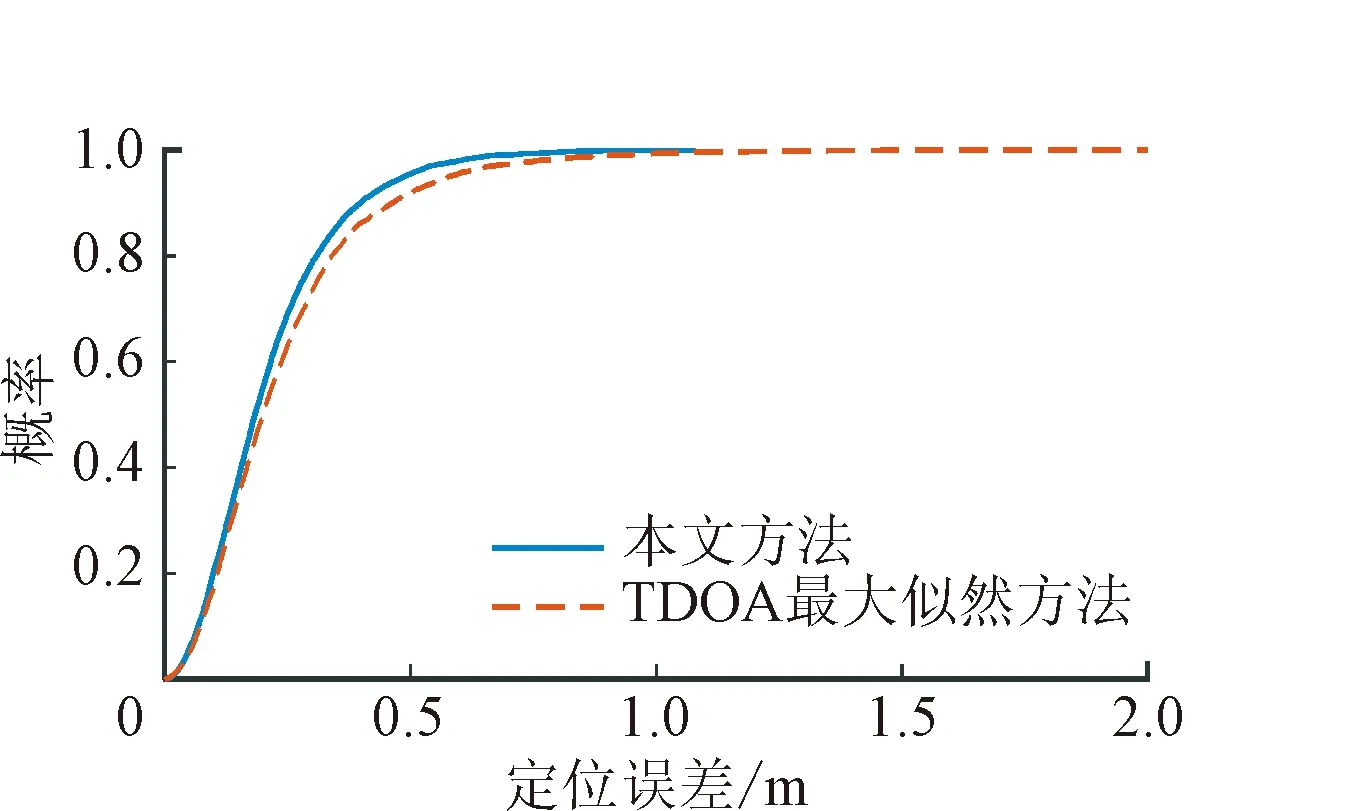
图8 多径噪声条件下的定位性能对比Fig.8 The comparison of positioning performance under multipath effect with

4.3 基站数量对定位结果的影响

通过不同基站数量条件下的数值仿真,对本文方法的性能进行评估。在无多径噪声情况下,量测噪声水平设定为σd=0.4、σv=0.3,短时位置序列长度T=4。分别评估4基站、3基站和2基站条件下的定位性能,结果如图9和图10所示。

图9 基站数量为4时两种方法定位性能对比Fig.9 The comparison of positioning performance under 4 beacons

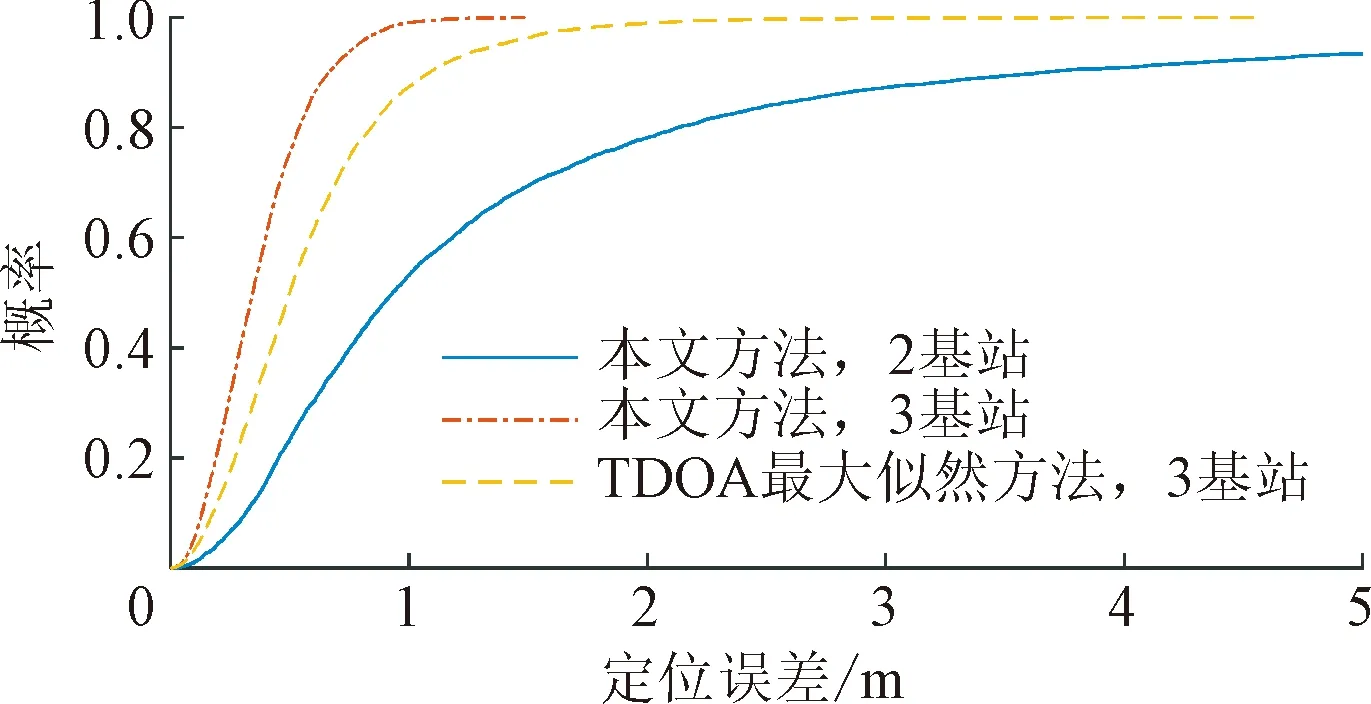
图10 基站数量为2和3时的定位性能对比Fig.10 The comparison of positioning performance under 2 beacons and 3 beacons

从图9和图10中可以看出,当基站数量不少于3个时,本文方法全面超越TDOA最大似然估计方法。当基站数量为3时,TDOA具有多个解析解,需要通过具有范围约束的最大似然估计法来进行求解。当仅有2个基站时,基于TDOA的定位架构将失效,无法实现有效的位置估计。本文方法,仍然能够在仅有2个基站的条件下实现有效的定位,如图10 所示,定位精度优于1.1 m的概率为60%,优于2.1 m的概率为80%。

图11所示为仅有2个基站时,本文方法的定位结果。与仿真轨迹的前半段相比,后半段的定位误差明显增大。这是由于基站数量较少,距离差所提供的信息量不足以消除相对速度测量误差所带来的不确定性,致使产生了较大的累积误差。但是,与传统TDOA架构所需的4个定位基站相比,本文方法将定位所需的基站数量减少至2个基站。

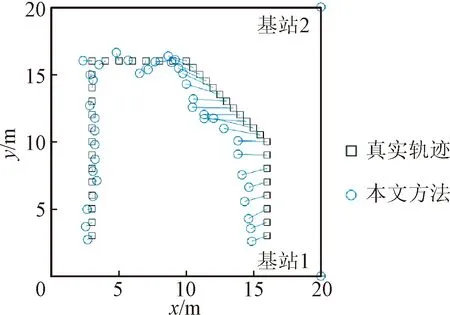
图11 二维场景2个基站时本文方法定位结果与真实轨道对比Fig.11 The positioning results with 2 beacons under 2D scenario

因此,相较于已有算法,在不同的基站部署密度条件下,本文方法均能够获得更高的定位精度。随着基站数量的增加,TDOA最大似然法的性能逐渐接近本文方法。在较低基站部署密度条件下,本文方法的性能优势则更为明显。

4.4 三维场景定位仿真

本节通过数值仿真对本文方法在3维场景中的定位性能进行评估。如图12所示为,在20 m×20 m×20 m的场景内布设4个基站,基站位置为[0,0,0]、[20,20,0]、[20,0,20]和[0,20,20] m。携带智能移动终端的目标在场景内从位置[3,3,7] m,经[3,16,7]、[10,16,7]和[15,10,13] m运动至[16,3,13] m。噪声水平设定为σd=0.4、σv=0.3,短时位置序列长度T=4。定位结果如图12所示,本文方法在三维场景中同样具有较好的定位精度和稳定性。两种方法三维场景的定位性能评估结果如图13所示,本文方法全面优于TDOA最大似然法,其定位精度优于0.49 m的概率为60%,优于0.73 m的概率为90%。

图12 三维场景4个基站的定位结果 Fig.12 The positioning results with 4 beacons under 3D scenario

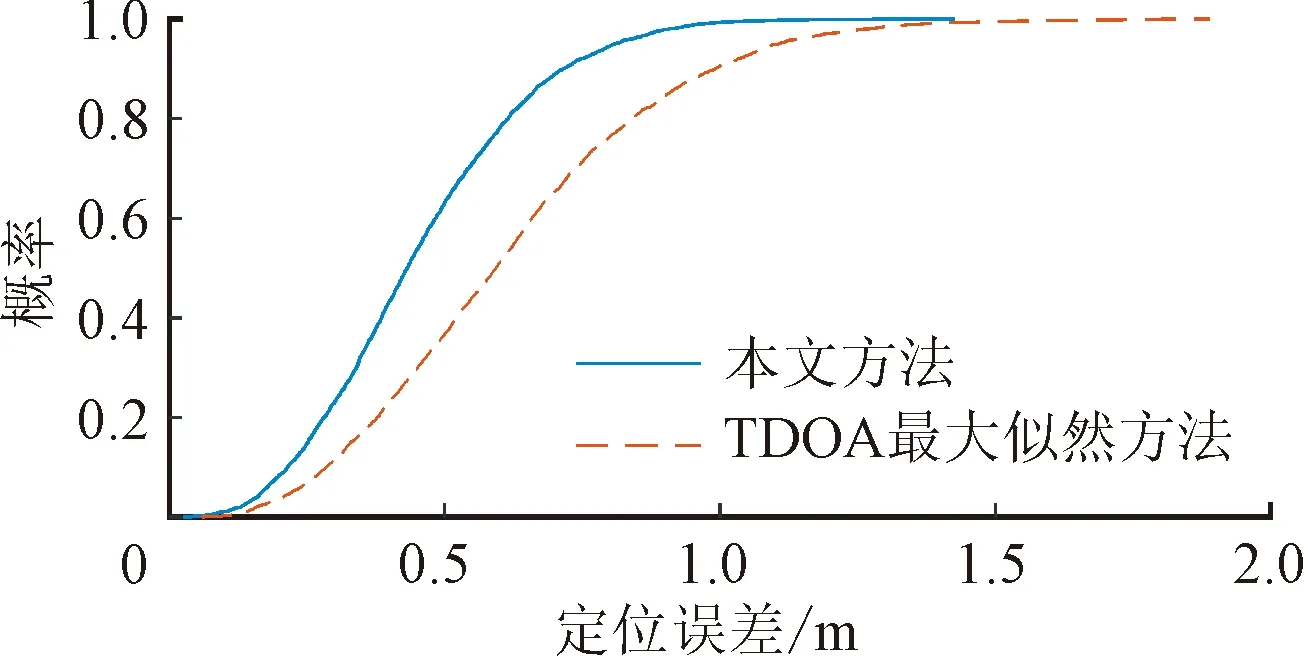
图13 三维场景的定位性能对比Fig.13 The comparison of positioning performance under 3D scenario

当基站数量为2和3时,传统TDOA定位架构失效,本文方法的性能如图14所示。当基站数量为2时,非线性最小二乘问题具有解析解,但解不唯一。这使得在计算过程中,LM算法收敛于“非最优解”时,致使沿着错误方向进行相对速度的积分,引起系统振荡而发散。当基站数量为3时,与二维场景下2个基站定位场景相似,由于基站数量较少,距离差所提供的信息量不足以消除相对速度测量误差带来的不确定性,致使随着时间的累积,产生了较大的累积误差,定位性能优于2.4 m的概率为60%,优于4.1 m的概率为90%。但是,与传统TDOA架构所需的5个定位基站相比,本文方法将定位所需的基站数量减少至3个基站。

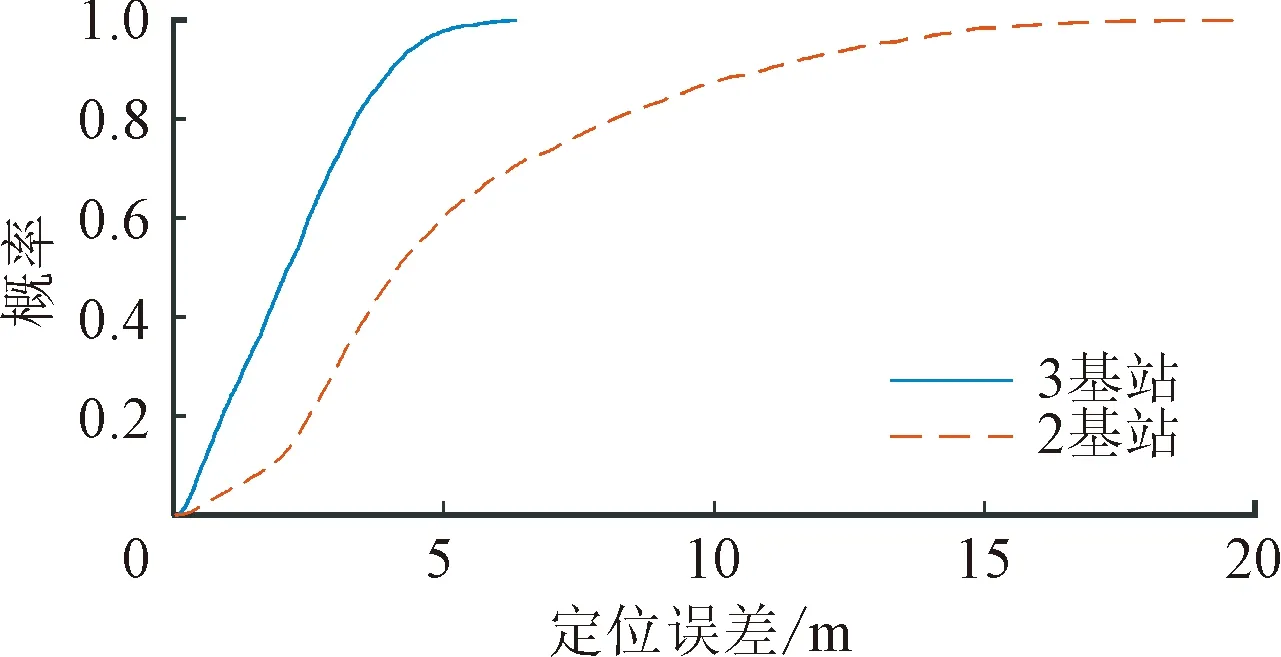
图14 本文方法基站数量为2和3时的定位性能Fig.14 The positioning performance under 2 beacons and 3 beacons

综上所述,本文方法无论是在二维还是三维场景中,均具有更高的定位精度和稳定性。同时,将异步定位所需的基站数量分别减少至2个和3个,可以有效应对现实中低基站部署密度的场景,在实际应用场景中,具有较好的应用价值。

5 实验与结果分析

5.1 实验设备及场景描述

通过在实际场景中进行实验对本文所提出的异步定位方法进行性能评估。为了便于定位误差统计,选用二维定位场景,长安大学本部北院主教学楼三楼大厅内,场景内有4个支柱结构,如图15所示。实验空间约为20 m×7 m,以左侧墙壁和立柱结构外沿延伸线的交点为空间坐标原点。所选实验设备为实验室自主开发的定位系统,如图16所示。播音节点和录音节点基于LoRa技术,通过同步节点实现高精度的时钟同步,进而可进行同步定位实验和异步定位实验。音频芯片为WM8978,扬声器和麦克风均选用消费级MEMS元器件,声组件的总成本低于40元。

图15 异步定位实验场景Fig.15 Experimental scenario for asynchronous positioning

(a)同步节点

本次实验中,用于声音伪距及相对运动速度量测估计的复合HFM信号时频如图17所示。信号采样率为48 000 Hz,时域带宽为0.05 s,抑制频率泄漏的前后缀时域带宽为0.01 s,下降信号成分的最低和最高频率为16 555 Hz和18 555 Hz,上升信号成分的对应频率为19 555 Hz和21 555 Hz,定位更新频率为1 Hz。

图17 复合HFM信号时频图Fig.17 The time frequency distribution of composite HFM signal

在场景内布设3个基站(播音节点),基站高度为1.8 m,如图18所示,基站坐标位置分别为[1.32,6.34]、[19.18,6.12]和[10.21,0.93] m。实验者手持录音节点,高度约为1.5 m,以正常步速沿着地面白线进行绕场行走。测量行走路线的位置作为定位参考真值,以此对本文方法的定位性能进行评估。

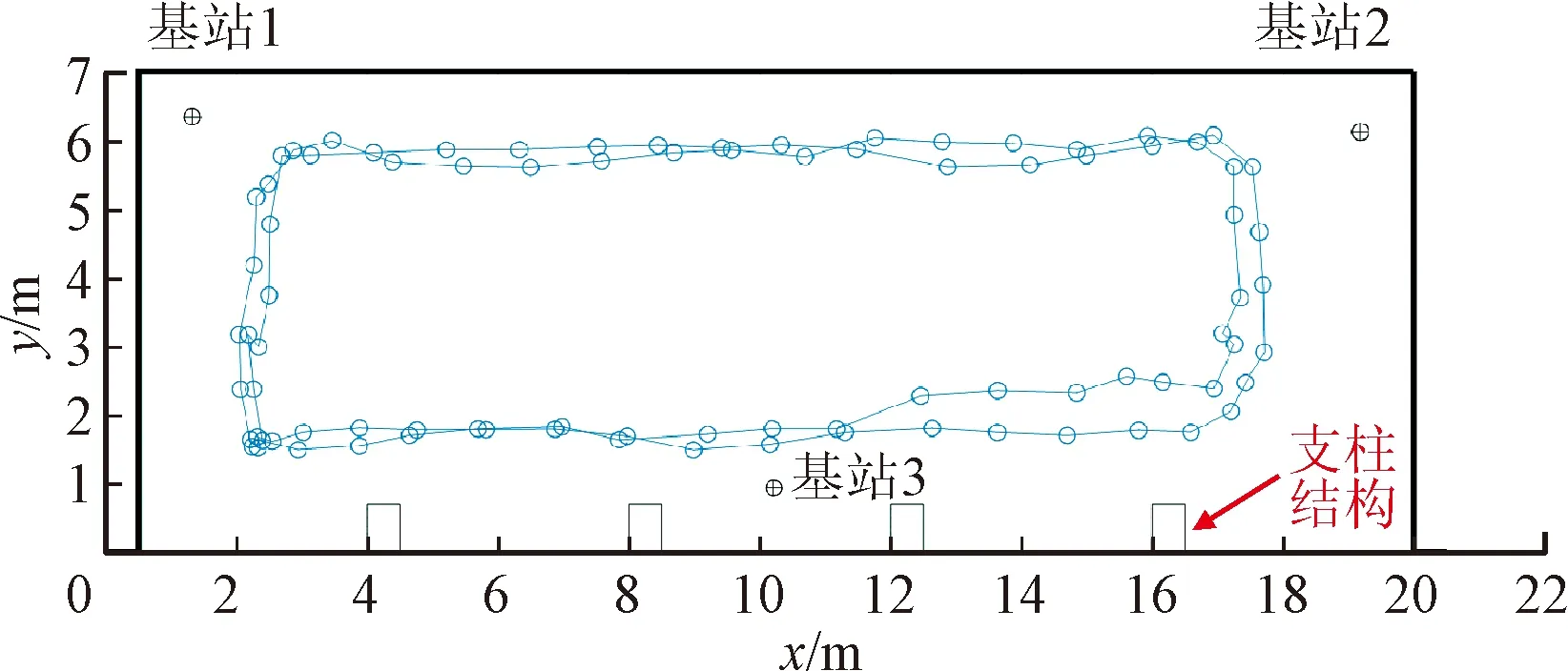
图18 本文提出的异步定位方法的定位结果Fig.18 The positioning result of our proposed asynchronous positioning method

5.2 实验结果分析

选择短时位置序列帧长T=2,迭代次数nmax=20,阈值ε=0.15,更新步长a1=0.3,回退步长a2=0.1,声速c=340 m/s,利用本文方法进行位置估计,结果如图18所示。同时,基于参数空间搜索求解TDOA和TOA最大似然估计方法进行位置估计,结果如图19和图20所示。

图19 基于TDOA最大似然估计方法的定位结果Fig.19 The positioning result of ML-based TDOA

通过对比可以看出,本文方法具有更高的稳定性。为了统计定位结果的误差分布,将位置估计结果到行进路线的垂直距离作为定位误差,3类定位方法的误差累积分布函数对比如图21所示。基于TDOA最大似然方法具有最低的定位精度,本文方法具有最高的定位精度,90%的概率优于0.43 m。当序列帧长度为T=3时,90%的概率优于0.29 m。

图21 实验结果的误差累积分布函数对比Fig.21 The comparison between experimental results’ CDF

通过实验结果分析,本文所提出的基于距离差和相对速度对多时刻位置进行联合异步估计的方法,能够在低基站部署密度环境中,实现高精度的位置估计,同时具有较好的定位稳定性。

6 结 论

本文针对智能移动终端的高精度室内定位需求,开展低基站部署密度条件下的异步声音定位方法研究。通过将定位过程视作马尔科夫链,结合距离差和相对速度,建立了短时位置序列的联合估计模型,采用LM算法对该高维度非线性问题进行快速求解,设计了迭代优化过程来提高位置估计精度和稳定性。对比数值仿真和实验结果,得到以下结论。

(1)本文所提出方法能够在低基站部署密度下实现高精度的室内异步定位。与现有方法相比,无论是二维还是三维定位场景,本文方法均具有更高的定位精度和稳定性。

(2)与现有方法相比,定位所需的最少基站数量在二维和三维场景中分别减少至2个和3个。较低的基站部署密度意味着较低的应用成本以及较强的遮挡环境适应能力,具有较高的工程应用价值。

(3)本文所提出方法能够有效应对较强的室内多径传播效应,可以提高系统在实际应用中的定位性能,为声技术在室内定位中的应用和推广提供方法和工具。