多普勒雷达下的机动多目标跟踪算法
国强,卢宇翀,戚连刚,KALIUZHNY Mykola
(1. 哈尔滨工程大学信息与通信工程学院,150001,哈尔滨; 2. 先进船舶通信与信息技术工业和信息化部重点实验室,150001,哈尔滨; 3. 哈尔滨工程大学物理与光电工程学院,150001,哈尔滨;4. 哈尔科夫国立无线电电子大学,61166,乌克兰哈尔科夫)
在多普勒雷达跟踪目标过程中,通过利用多普勒量测[1](径向速度)可以有效抑制杂波,显著提升跟踪器性能。但是,由于传感器的物理限制,当目标的多普勒量测小于最小可检测速度(MDV)时,目标就无法被传感器检测,造成多普勒盲区(DBZ)[2],导致航迹断续、暂消、重起批、断批等问题。
为了解决这个问题,Gordon等将DBZ作为先验信息应用到粒子滤波算法中[3]。在此基础上,文献[4]提出多模型粒子滤波器,用来跟踪DBZ遮掩的机动目标。此外,一些学者结合多模型算法[5],通过添加运动停止模型来解决这个问题。Koch等给出另一种解决方案,将 MDV作为是一个传感器状态参数,把目标检测概率描述为一个与之相关的状态函数[6-7],当目标进入DBZ后获得一个较低的检测概率,通过引入伪量测来表示漏检。
面对更复杂的多目标场景,文献[8]提出“双虚拟”分配方法,额外加入虚拟量测表示由于DBZ引起的漏检,让目标在漏检后依旧可以使对应航迹保持“活动”。文献[9]通过使用基于航迹-航迹关联的方法,通过拼接属于同一目标的断裂航迹段来提高航迹连续性。上述的多目标跟踪方法都需要经过复杂的数据关联过程,而基于随机有限集(RFS)的多目标跟踪算法可以避免这一过程,大大减少了算法的计算复杂度。文献[10]通过将文献[6]中的概率检测模型扩展到高斯混合概率假设密度(GM-PHD)滤波器上,实现在DBZ遮掩下的多目标跟踪,文献[11]将其应用到带势概率假设密度(CPHD)滤波器上。但是,这些文献都只利用了MDV信息而忽略了多普勒量测。对此,文献[12]同时利用多普勒量测信息和MDV信息,给出GM-PHD的详细推导过程。
上述算法并不能跟踪机动目标,为解决这个问题,研究者提出了很多基于随机有限集的多模型算法。例如,多模型概率假设密度(MM-PHD)[13]、多模型带势概率假设密度(MM-CPHD)[14]、多模型多伯努利(MM-MB)[15]、多模型标签多伯努利(MM-LMB)[16]。多模型广义标签多伯努利(MM-GLMB)[17-18]。但是,这些多模型算法会不可避免的出现马尔科夫跳变分支规模指数增长的情况,所以上述算法均采用剪枝近似的方式对分支数量进行控制。与多模型(MM)算法不同,交互多模型算法(IMM)采用条件概率的分支合并策略,可以有效地控制分支数量,文献[19]将IMM算法应用到广义标签多伯努利(GLMB)滤波器中,提出交互多模型广义标签多伯努利(IMM-GLMB)滤波器,在跟踪精度和计算复杂度方面均优于基于分支剪枝策略的MM-GLMB算法。
在目标跟踪过程中,目标的航迹起始条件通常作为先验信息被人们所忽视,在实际应用过程中,能利用的信息只有传感器的量测。为了让跟踪器正常运行,文献[20-21]通过使用连续几帧的量测构建新生目标密度,文献[22]提出了联合单点和两点差分航迹起始算法的目标新生强度自适应估计方法,但这些算法均最少需要两步才可以确认速度信息。
为了跟踪DBZ遮掩下的机动多目标,本文通过利用文献[6]中的检测概率模型结合IMM算法,提出并入MDV信息的IMM-GLMB滤波器,相比于PHD具有更好性能表现,并且可以提供航迹的标签信息。最后,针对航迹起始问题,利用多普勒量测中隐含的速度信息,提出一种适用于GLMB滤波器的自适应航迹起始算法。为了证明算法的有效性,给出了GLMB和PHD的详细性能比较以及在不同状态转移矩阵下的鲁棒性分析。实验结果表明,在不同DBZ宽度下GLMB都具有更好的性能表现,并且可以在较短时间内完成航迹起始,同时采用IMM算法在运行时间上比MM算法减少了34%左右。
1 并入MDV信息的检测概率模型

(1)
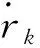
(2)


(3)
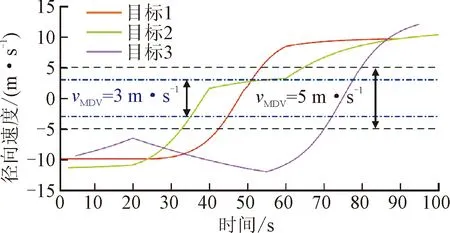
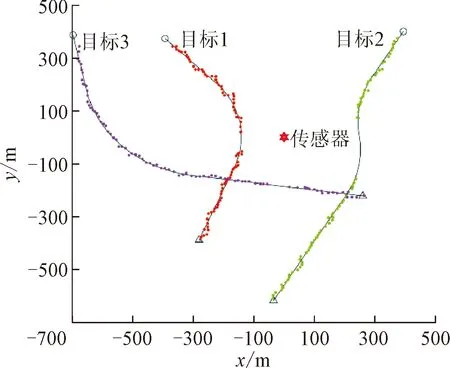
杂波凹口的主要作用是抑制杂波,同时也会对低多普勒频率运动目标的检测概率产生影响。当目标进入多普勒盲区时,即nc pD,k(x)≈pD[1-exp(-(nc(xk)/vMDV)2log2)] (4) 由于检测概率为指数形式,需要先转换成高斯形式在进行后续的调用,根据文献[12]将检测概率建模为 (5) (6) 伪量测矩阵为 (7) (8) 设在k-1时刻有N个目标,则多目标状态为X={x1,x2, …,xN},其中xi=[xi,μi,li],x、μ、l分别表示目标的运动状态、运动模型和标签状态。定义马尔科夫模型跳变转移概率矩阵为 (9) 式中:χ(μi|μj)表示运动模型由μj跳变到μi的概率。 目标运动到k时刻,状态由x跳转到x+,则马尔科夫状态转移密度表示为 φ(x+,μ+,l+|x,μ,l)=φ(x+|x,μ+,l)χ(μ+|μ) (10) IMM算法通过模型条件概率对目标运动状态进行混合,这里给出经过模型状态混合后的IMM-GLMB的多目标先验密度 π+(X+)= (11) 式中:上标(c)表示不同的GLMB分量。其中预测集权重为 (12) 单目标混合密度为 I (13) 存活目标和新生目标的单目标密度分别为 (14) (15) 存活目标预测密度的权重为 (16) (17) 存活目标在进行时间预测前需要根据IMM算法进行状态混合 (18) (19) 式中:上标o表示预测分量的初始状态。 (20) (21) 新生目标预测密度的权重为 (22) 式中:上标l、l′对应不同的航迹信息。 由于新生目标没有先验模型概率,所以不需要模型混合步骤,可直接计算新生目标的均值和协方差 (23) (24) 设k时刻的量测集为Z={z1,z2,…,z|Z|},z=[yc,yd],yc表示位置量测信息,yd表示多普勒量测信息。此时多目标后验密度为 π(X|Z)= (25) 其中在模型μr下的单目标后验概率密度为 p(c,θ)(x,μ,l|Z)= (26) 更新权重为 (27) 单目标归一化常量为 (28) 式中:θ(l)表示标签为l的航迹关联映射,当θ(l)=0时,说明量测与航迹没有关联,此时航迹漏检,θ(l)>0时,说明航迹与量测信息进行了更新;δ0(θ(l))表示广义克罗内德耳塔函数。 (29) (30) (31) (32) (33) 其中伪量测增益Ki,f由下式给出 (34) 式中伪量测新息协方差为 (35) (36) (37) (38) (39) (40) (41) 式中:Hc表示目标观测矩阵。位置量测的增益和新息协方差分别为 (42) (43) 然后利用多普勒信息yd进一步更新 (44) (45) (46) 位置分量的权重为 (47) (48) 多普勒量测增益和协方差为 (49) (50) 式中:Rc和σd分别为位置量测和多普勒量测噪声标准差,多普量测的雅克比矩阵为 Hd(m)=[h1,h2,h3,h4] (51) (52) (53) (54) (55) (56) 其中增强量测的增益和协方差为 (57) (58) (59) 所有分量在计算完成后需要进行模型状态混合才能进行目标状态提取。根据IMM算法可给出模型混合过程为 (60) (61) (62) 模型概率更新过程由下式给出 (63) 速度信息筛选规则为 (64) 多普勒信息筛选规则为 (65) (66) (67) (68) (69) 已知多普勒量测方程为 hd,k= (70) 通过观察,将式(70)构造为 (71) 其中 (72) (73) 速度分量的协方差[23]为 (74) 本节设置一个二维场景,分别比较IMM-PHD-MDV-ATI和IMM-GLMB-MDV-ATI两种滤波器在最小可检测速度vMDV为3和5时的跟踪性能,传感器位置设置在(0,0) m,传感器量测周期为1 s。观测场景为[-1 000, 1 000] m×[-1 000, 1 000] m。 每个目标都可以在3种不同的运动模型中随机改变运动状态。模型一(μ=1)是匀速运动模型(ω=0),模型二(μ=2)是转弯速率为2°/s的协同转弯模型(ω=2π/180),模型三(μ=3)是转弯速率为-2°/s的协同转弯模型(ω=-2π/1)。3种模型对应的状态转移矩阵如下 F(μ)=F(ω)= 噪声协方差矩阵为 式中:T=1 s; 过程噪声标准差σp=10 m/s。 表1 目标的运动状态 目标的初始状态为 在场景一中,比较固定航迹起始位置和使用自适应航迹起始(ATI)算法的GLMB和PHD两种滤波器的性能。3个目标的航迹起始位置分别设置为 目标运动模型之间切换的马尔可夫矩阵设置为 图1表示目标的径向速度的变化情况,|nc(x,xs)| 图1 目标的多普勒与相应的DBZ随时间变换关系 Fig.1 Time varying relationship between target Doppler and corresponding DBZ 图2、图3给出当vMDV=3 m/s时的单次运行结果,显示了两个跟踪器的真实轨迹和估计轨迹。可以发现,在目标经过多普勒盲区后标签没有发生变化,同时GLMB相比于PHD跟踪器在多普勒盲区中可以保留更多的目标状态信息,尤其是当多普勒盲区范围较小时GLMB基本不会受到影响。 图2 IMM-PHD-MDV的跟踪结果Fig.2 IMM-PHD-MDV tracking results 图3 IMM-GLMB-MDV的跟踪结果Fig.3 IMM-GLMB-MDV tracking results 图4~图7给出了经过100次蒙特卡罗仿真实验后几种算法的性能比较。当vMDV=3 m/s时,在0~5 s时间内目标陆续出现,由于航迹起始算法缺少先验信息,OSPA误差起伏较大,但是算法可以在3 s内快速收敛。目标数量估计快速上升并在6 s时接近真实数量,8~35 s所跟踪的3个目标完成航迹起始并且没有被多普勒盲区遮掩,这段时间OSPA误差最小,目标数量估计与真实数量相同,跟踪算法可以有效运行。在36~55 s时,目标开始出现被多普勒盲区遮掩的情况,OSPA开始以较快的速度恶化并在49 s左右到达顶峰,目标数量估计也随之减少。由于此时目标1和目标2均处于多普勒盲区当中,量测信息丢失,导致这期间跟踪器无法跟踪到目标。在51 s和55 s两个目标先后驶出多普勒盲区,跟踪器重新接收到量测信息可以很快恢复正常。在73~77 s时,目标3经过多普勒盲区,由于时间较短对跟踪器造成的影响有限。 图4 vMDV=3 m/s时不同算法的OPSA误差Fig.4 OPSA error of different algorithms when vMDV=3 m/s 图5 vMDV=3 m/s时不同算法的目标数量估计Fig.5 Estimation of the number of targets under different algorithms vMDV=3 m/s 图6 vMDV=5 m/s时不同算法的OPSA误差Fig.6 OPSA error of different algorithms when vMDV=5 m/s 图7 vMDV=5 m/s时不同算法的目标数量估计Fig.7 Estimation of the number of targets under different algorithms when vMDV=5 m/s 从实验可以看出,GLMB整体性能要优于PHD跟踪器,在经过多普勒盲区时性能恶化程度明显要小于PHD。在航迹结束后的3 s内GLMB的OSPA性能出现波动,因为PHD滤波器在目标量测消失后会立即丢失这段时间的估计,而GLMB则会保留一段时间,进而导致在航迹结束时OSPA误差变大。与固定航迹起始的情况相比,应用自适应航迹起始算法的GLMB滤波器可以更快趋于稳定,并且在性能稳定后两种滤波器与固定航迹起始情况比较性能表现基本一致。 在多模型滤波场景中,模型转移概率是非常重要的参数,然而模型状态转移矩阵作为先验信息,通常无法提前确认。这里重复测试了所提滤波器在3种不同状态转移矩阵下的性能比较,在vMDV=3 m/s的前提下,其余参数与场景一中相同,进行了100次蒙特卡罗仿真实验。 3种不同的马尔科夫矩阵如下 在给出的状态转移矩阵中,对角线上的元素要大于其他元素,说明在任意时刻,目标状态保持在当前运动模型上的概率要比运动模型发生变化的概率大。图8比较了3种不同状态转移矩阵下的OSPA误差,可以看出,比较选用不同的状态转移矩阵滤波器的性能表现基本一致,说明本文滤波器对模型状态转移矩阵的变化具有较强的鲁棒性。 图8 不同状态转移矩阵下的OSPA误差 Fig.8 OSPA errors under different state transition matrices 图9 不同状态转移矩阵下的目标数量估计Fig.9 Target quantity estimation under different state transition matrices 由图8可以发现,在状态转移矩阵为M3时滤波器的性能表现最好,然而相比去其他情况的性能提升可以忽略不计,证明本文滤波器对于模型状态转移矩阵的参数变化上具有良好的容忍度。 该实验场景中比较了基于分支剪枝策略的多模型算法与基于分支合并策略的交互多模型算法在运算精度和计算效率之间的差距。这里在vMDV=3 m/s的前提下,其余参数与场景一中相同,进行了100次蒙特卡罗仿真实验。 通过图10可以看出,IMM算法的跟踪精度要略优于MM算法,因为MM在进行分支裁剪过程中会损失一部分有效信息,而IMM采用分支合并策略会更大程度上保留有效信息。通过仿真实验对比了MM-PHD-ATI、IMM-PHD-ATI、MM-GLMB-ATI、IMM-GLMB-ATI 跟踪器的单步运行时间,分别为0.048、0.031、6.594、4.417 s。可以看出,使用IMM的跟踪算法比使用MM的算法在计算时间上提升34%左右,其中MM-GLMB-ATI算法消耗时间最长,而IMM-PHD-ATI算法消耗时间最少。尽管PHD算法的运行效率更高,但在跟踪精度方面不尽人意,尤其是在多普勒盲区遮掩时基本完全失去对目标跟踪信息。由于PHD本身的限制,MM-PHD-ATI算法无法输出标签信息,不能提供航迹信息。 图10 不同算法的OSPA误差Fig.10 OSPA error of different algorithms 图11 不同算法的目标数量估计Fig.11 Estimation of the number of targets under different algorithms 综上,在多普勒雷达的场景下所提算法可以有效抑制多普勒盲区的影响,尤其是在多普勒盲区范围较小时,造成的影响可以忽略不计。通过比较固定航迹起始位置和使用自适应航迹起始算法两种情况,证明了所提出的航迹自适应起始算法的正确性。 在多普勒雷达的应用场景下,根据最小可检测速度和交互多模型算法,提出了IMM-GLMB-MDV滤波器并给出详细的推导过程,比IMM-PHD-MDV具有更好的性能表象。利用最小可检测速度对检测概率建模一定程度上抑制了多普勒盲区的影响,并通过单独的航迹自适应起始算法,使滤波器不再需要固定目标初始位置,结果显示,算法可以在较短时间内完成航迹起始。所提算法在多普勒盲区下的机动多目标跟踪领域具有一定的工程应用价值。
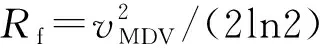

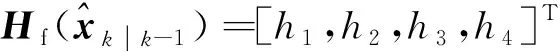

2 IMM-GLMB-MDV滤波器
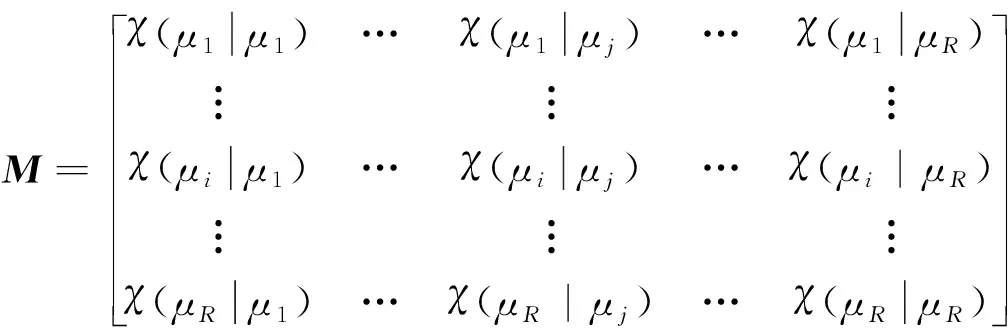
2.1 预测
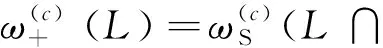
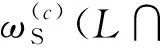
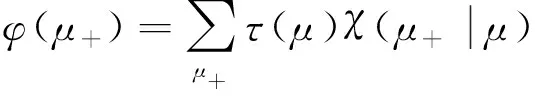
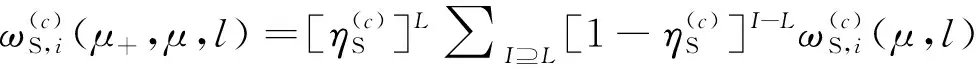


2.2 量测更新
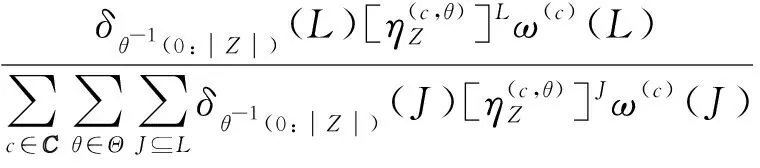


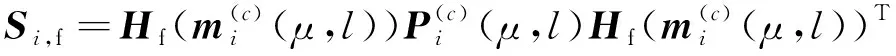

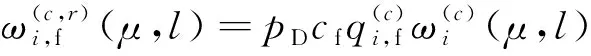



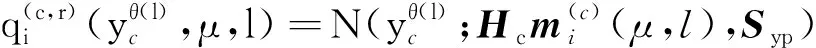
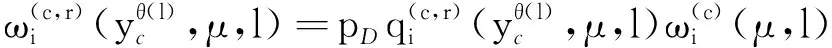
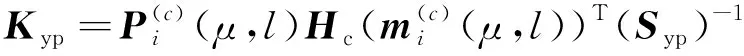
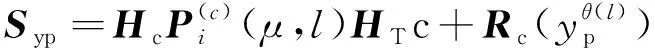
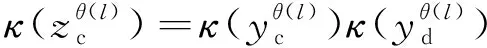
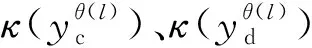
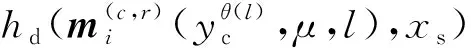
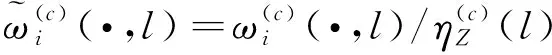
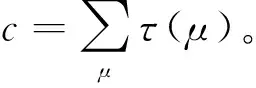
2.3 自适应航迹起始


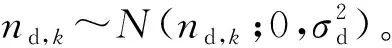

3 仿真验证
3.1 仿真参数设置


3.2 实验场景一



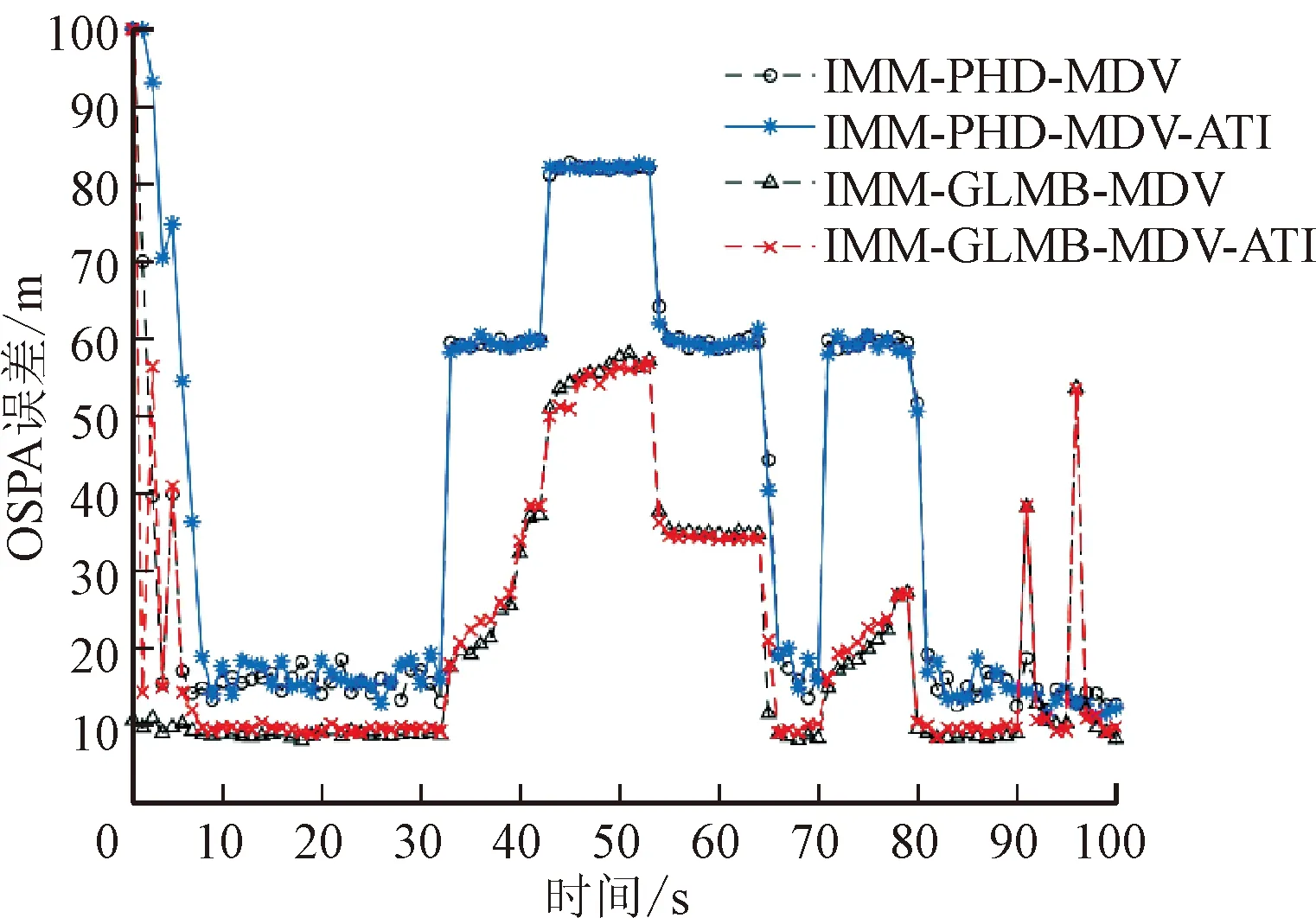

3.3 实验场景二
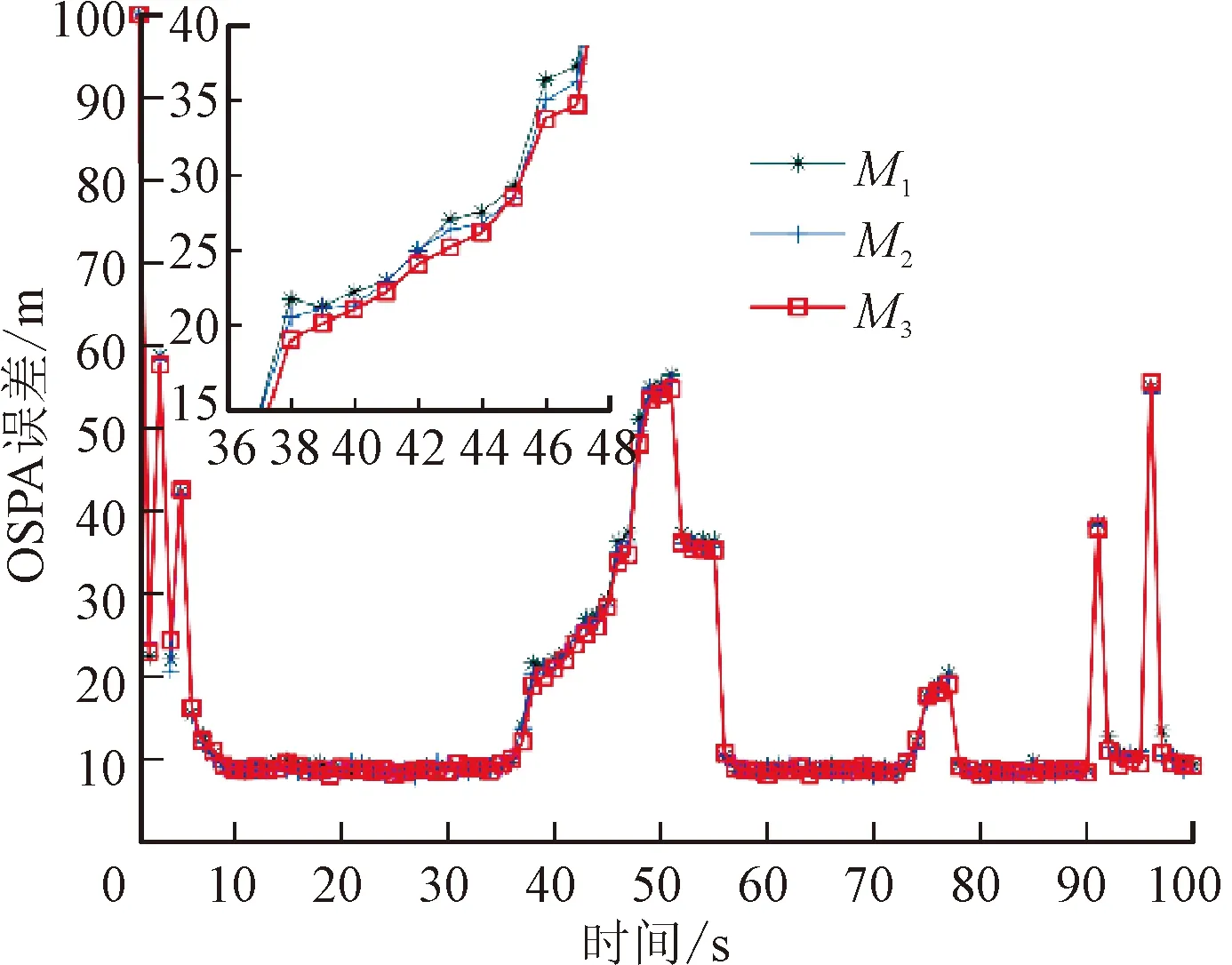

3.4 实验场景三


4 结 论

