盾构隧道开挖面被动失稳的不排水效应分析

王海峰 康 博 李鹏飞 刘增辉 狄启光 陈柯屹

（1.南通铁建建设构件有限公司，江苏南通 226000；2.北京工业大学城市安全与灾害工程教育部重点实验室，北京 100124；3.中国奥园集团股份有限公司，广东广州 511442）

0 引言

盾构法凭借其自动化程度高、安全与快速相协调、对既有建筑物扰动小等性能优点，逐渐成为城市地铁轨道建设的主要施工方法[1-2]。维持盾构开挖面稳定一直是盾构施工过程中的重点问题，其关键在于确定开挖面上合理的支护力范围，开挖面支护力过小易造成地表不均匀沉降等开挖面失稳事故，相反，则会引起地表开裂隆起等事故。

当前关于开挖面稳定性的理论分析解析方法主要有极限分析法和极限平衡法[3]。Leca 和Dormieux[4]构建了一个延伸到地表且开口朝上的倒锥体形态的被动破坏机制。Soubra 等[5-6]改进并提出了一种由多个刚性截锥体组成的三维刚性块破坏机制。刘志[7]分别从地表隆起破坏模式和开挖面极限支护力两个方面，分析了浅覆地铁盾构的稳定性问题。

一些学者采用数值模拟与室内试验的方法开展了无水地层的盾构隧道开挖面稳定性分析[8-11]。工程实际情况往往是盾构需带水作业，针对富水地层盾构隧道开挖面稳定性，国内外也展开了相关的研究和探讨。Anagnostou 等[12-14]分析了泥水注入和土压盾构施工中地下水渗流产生的渗透力影响。Lee 等[15-16]以Leca 等提出的无渗流破坏模式[4]为基础，采用上限法模型推导考虑渗流的总极限支护力公式。Lee等[17]分析了管棚预支护情况下考虑渗流的隧道开挖面稳定性。刘 维等[18]与王浩然等[19]认为渗流的影响不仅作用在整个失稳土体内，并采用极限分析上限法推导了考虑渗流影响的总极限支护力的公式。

目前，对于盾构隧道开挖面最小支护力的研究较多，但对于盾构隧道最大支护力的研究相对较少。因此，为降低盾构隧道施工的风险，深入研究被动破坏的失稳机理及规律，具有重要的工程实践意义和科学研究价值。将饱和地层中的静力分析简化为理想情况，分为不排水效应和排水效应两种情形，不排水效应又称为短期效应，适用于渗流来不及发生且土体没有发生体积变形的情况，一般在低渗透性的黏土地层或隧道开挖和衬砌的施作速度很快时发生。

本文考虑地下水的渗流效应，整理现有的室内试验和理论研究成果，通过MATLAB 编程和FLAC3D数值模拟，提出一种隧道开挖面被动失稳的破坏模式，研究不排水条件下的盾构隧道开挖面稳定性，并在此基础上，分别针对均质土和成层土进行理论分析；选取典型案例开展数值模拟，将开挖面被动极限支护力的解析解与数值解进行对比，分析理论模型的适用性。

1 理论分析方法

1.1 破坏机制原理

在开挖面破坏机制理论计算方面，通常假定开挖面处的破坏区域形状是一个椭圆形，但当开挖面发生失稳，尤其是整体失稳时，开挖面上的破坏区域形状更接近圆形[8-20]。因此，假定开挖面上的破坏区域为内接圆形，土体是均质的各向同性弹塑性材料，符合莫尔-库仑强度准则，若假设土体的不排水抗剪强度cu不随深度变化，根据总应力法，土体的黏聚力应等于不排水的抗剪强度，内摩擦角应等于零。

根据离心机试验结果[21-23]，隧道开挖面的破坏区会逐渐向上发展，且向外倾斜，因不排水条件下上部破坏区向外倾斜的程度很小，因而可假定上部破坏区边界是近似竖直的。成层土不排水条件下的盾构隧道被动破坏机制模型如图1 所示，该破坏机制模型在隧道开挖面正前方由n个刚性截椭圆柱体组成，斜截圆柱体被垂直于纸面的平面相切，并且n个截椭圆柱体的角度之和为π/2，图2 演示了当n=2 时的该破坏模式的滑动。假设盾构隧道穿越的土层是均质的，隧道上方覆土层是非均质的且由n个水平层组成，当n=5时，计算结果的精度提升不大[7]，因此取5 个刚性截椭圆柱体组成开挖面前方的破坏模式，如图1（b）所示。

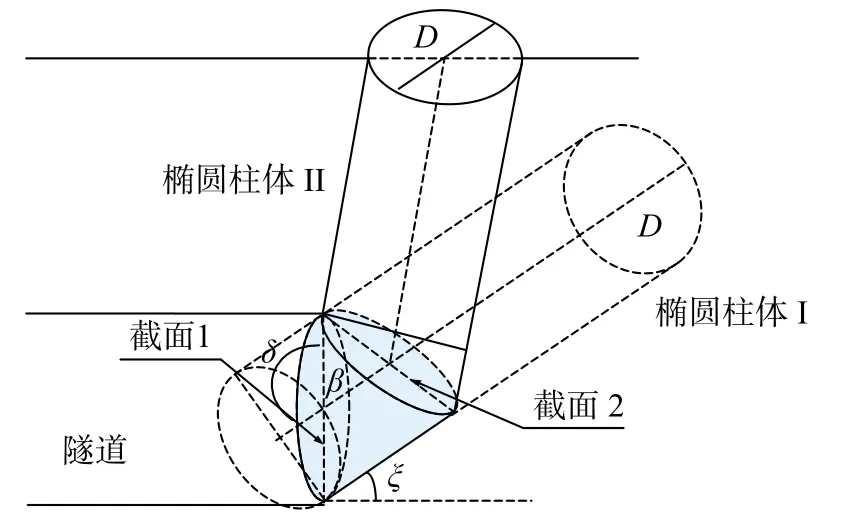
图2 两个块体的椭圆柱体破坏模式

1.2 几何关系

假定隧道直径为D，埋深为C，地表超载为σs，开挖面的支护压力假设为均布荷载σT。开挖面前方第i个刚性截椭圆柱体是由第i个椭圆柱体被第i个和第i+1 个截面所截（i=1,2,3,4,5），其截面均为直径为D的圆形，而破坏区上方竖直刚性椭圆柱体的底面为椭圆形，其长半轴长为D，短半轴长为d。βi为开挖面前方第i个截面和第i+1个截面的夹角，δi为第i个截面与第i个椭圆柱体轴线的夹角（i=1,2,3,4），δ5为最后一个斜椭圆柱体的斜截截面与其轴线的夹角。

假设第i个椭圆柱体的底面长半轴长为D，短半轴长为ai，被穿越层土体饱和重度为γ0，不排水抗剪强度为非均质覆土层第j层的土体饱和重度为γj，不排水抗剪强度为厚度为zj(j=1,2,···n)，且有z1+z2+···+zj+···+zn=C。

根据几何关系有：

刚性截椭圆柱体的体积Vi和侧面积Si（i=1,2,3,4,5）为

式中：A1为开挖面的面积；Ai,i+1为第i个刚性截椭圆柱体与第i+1 个刚性截椭圆柱体相交的圆截面面积。破坏区上方竖直刚性椭圆柱体底面的椭圆面积A6和周长l6[5]：

1.3 速度场

各个斜截圆柱体的滑动方向与圆柱体的轴线方向一致，且与速度间断面平行。速度矢量关系如图3所示。

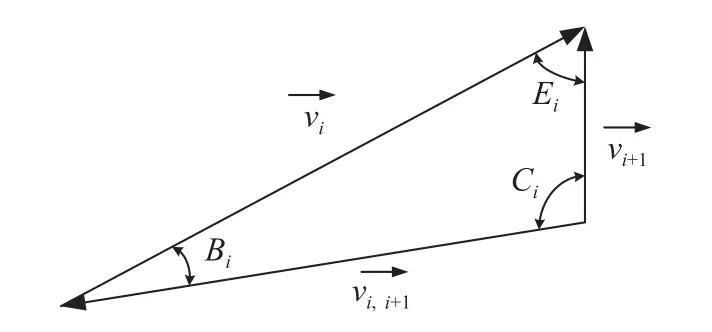
图3 速度矢量图

假设第i个刚性截椭圆柱体的速度为vi（i=1,2,3,4,5），由于刚体连续性，覆土层中竖直截椭圆柱的机动速度均设为v6，且方向竖直向下，第i个刚性截椭圆柱体和第i+1 个刚性截椭圆柱体的相对速度为vi,i+1，这里i=1,2,3,4，第5 个刚性截椭圆柱体和破坏区上方覆土层竖直刚性椭圆柱体的相对速度为v5,6，可得：

根据三角形正弦定理，得到速度表达式如下：

1.4 极限支护力求解

根据极限分析法上限定理，维持开挖面稳定的条件为

式中：Pe为外力虚功率；Pv为土体失稳模式中的内部能量耗散率。外力虚功率Pe由开挖面支护力的虚功率PT、地表超载的虚功率PS、破坏区土体重力的虚功率Pγ组成，即

开挖面支护力做功PT为

地表超载做功PS为

破坏区土体重力做功Pγ为

式中：Pγ1为穿越层即模型下部破坏区重力的虚功率；Pγ2为覆土层中n个截椭圆柱所在破坏区重力的虚功率。

隧道破坏区范围内部能量耗散率Pv为

式中：Pv1为发生在下部破坏区不同截椭圆柱表面和交界截面之间的内能耗散率之和；Pv2为下部破坏区与上部竖直截椭圆柱交界面的内能耗散率；Pv3为覆土层中各竖直截椭圆柱侧表面的内能耗散率。

均质土不排水条件下盾构隧道开挖面被动破坏时的极限支护力上限解为

式中：NS为地表超载对开挖面极限支护力的影响系数；Nγ为饱和重度对开挖面极限支护力的影响系数；Nc为土体不排水抗剪强度对开挖面极限支护力的影响系数。化简各个角度的几何关系后可得

此时，式（23）可以化为

将式（29）无量纲化后可得

其中，Nc由公式（29）确定。

将各个角度变量的变化范围作为约束条件，以式（26）为目标函数，采用MATLAB 软件对破坏区的形状进行优化，根据破坏模式编写约束条件函数如下（i=1,2,3,4,5）：

利用fmincon 函数求解可得到该破坏模式下σT的最优解，即为不排水条件下的盾构隧道开挖面的极限支护力。

1.5 均质土不排水

当覆土层与隧道穿越层的土体参数取值相同时，隧道的工况转化为均质土不排水条件，其破坏模式变化如图4 所示。

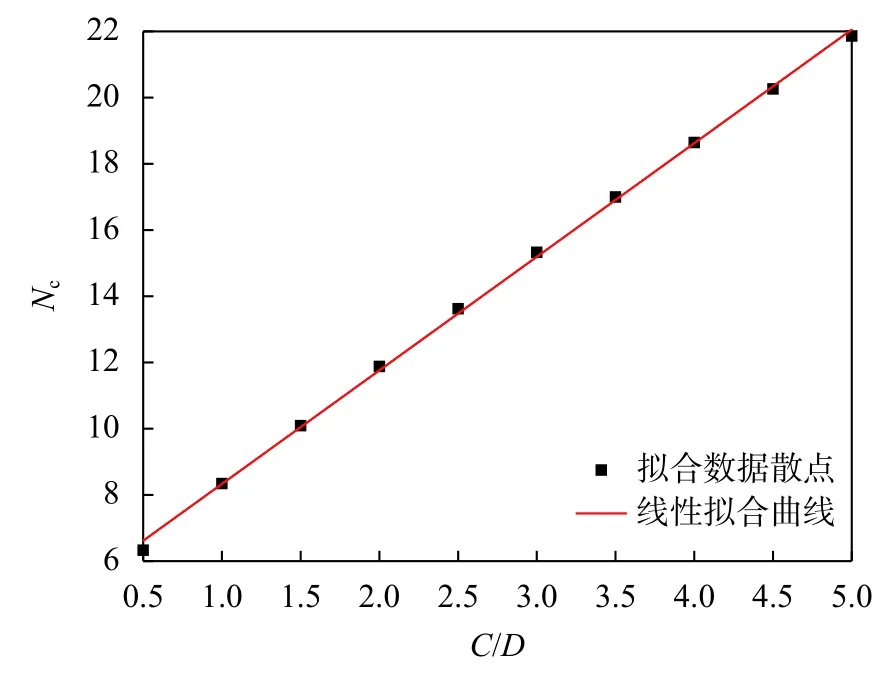
图5 Nc 随埋深比C/D 的变化规律

不排水条件下浅埋隧道开挖面被动破坏时极限支护力上限解表达式为

对式（38）无量纲化后可得

2 理论拟合公式

2.1 均质土不排水

Nc与埋深比C/D之间关系的拟合公式为

将式（43）代入式（38），可得

通过无量纲化后得到

由此，利用式（44）或式（45）可以快捷估算均质土层不排水条件下盾构隧道开挖面被动破坏时的极限支护力。

2.2 成层土不排水

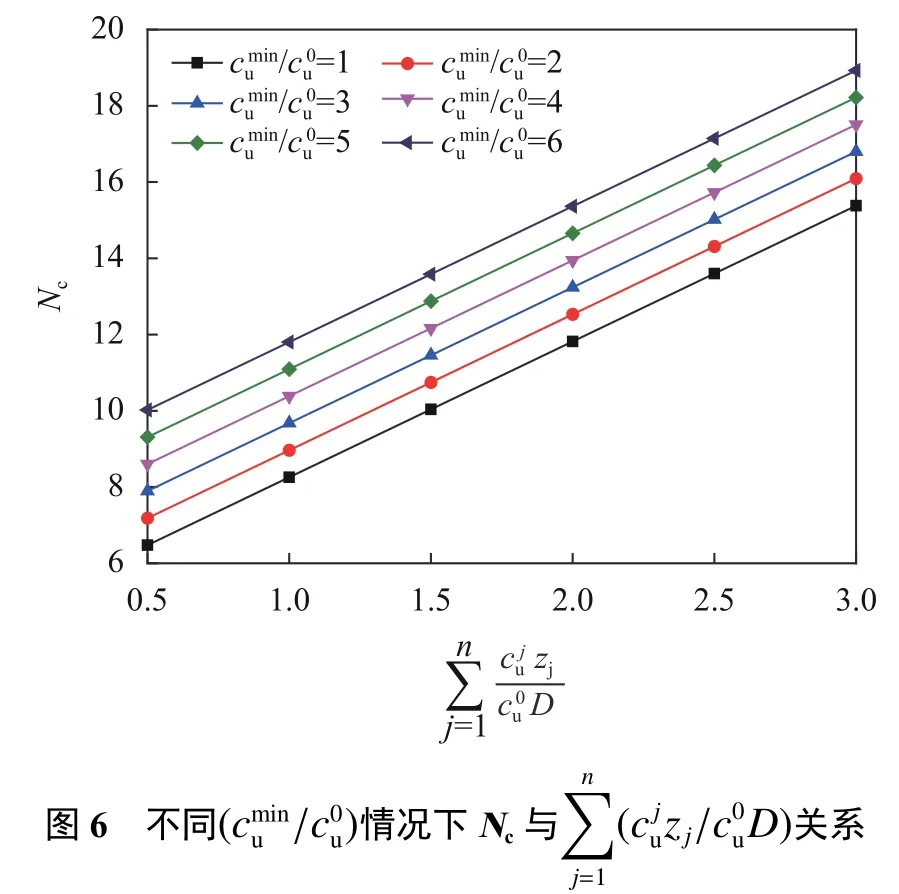
将式（46）代入式（32），可得

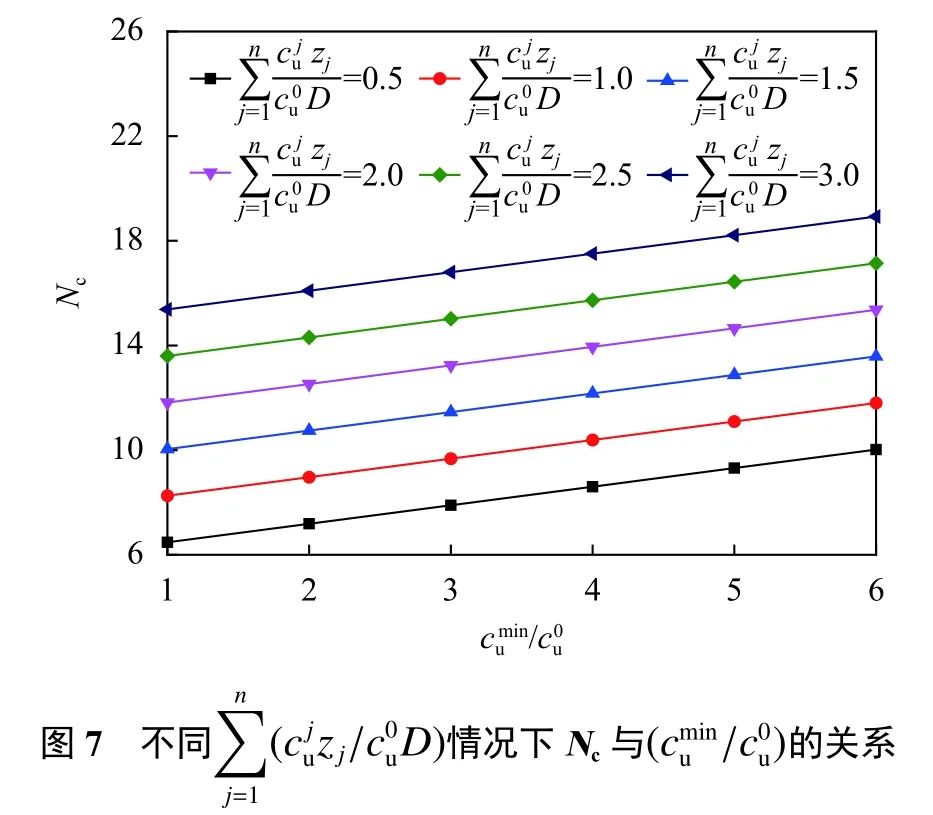
无量纲化后，可得

3 影响因素敏感性分析

不同γD/cu情况下，荷载参数(σT-σs)/cu与埋深比C/D的关系如图8 所示。从图8 可以看到，当重度参数γD/cu一定时，荷载参数(σT-σS)/cu随埋深比C/D的增大而线性增大，即同一地层，饱和重度和不排水抗剪强度为确定值时，隧道埋深比越大，保持开挖面被动稳定所需的极限支护力就越大。

图8 不同γD/cu情况下荷载参数(σT-σs)/cu与埋深比C/D 的关系

图9 给出了埋深比C/D一定时，荷载参数(σT-σS)/cu与重度参数γD/cu的关系。可以看到，随重度参数γD/cu的增大，荷载参数(σT-σS)/cu呈线性增大，这表示无论隧道埋深取什么值，当饱和重度增大或土体不排水抗剪强度减小时，被动极限支护力也逐渐增大，且隧道埋深取较大值时极限支护力的增大速度更快。

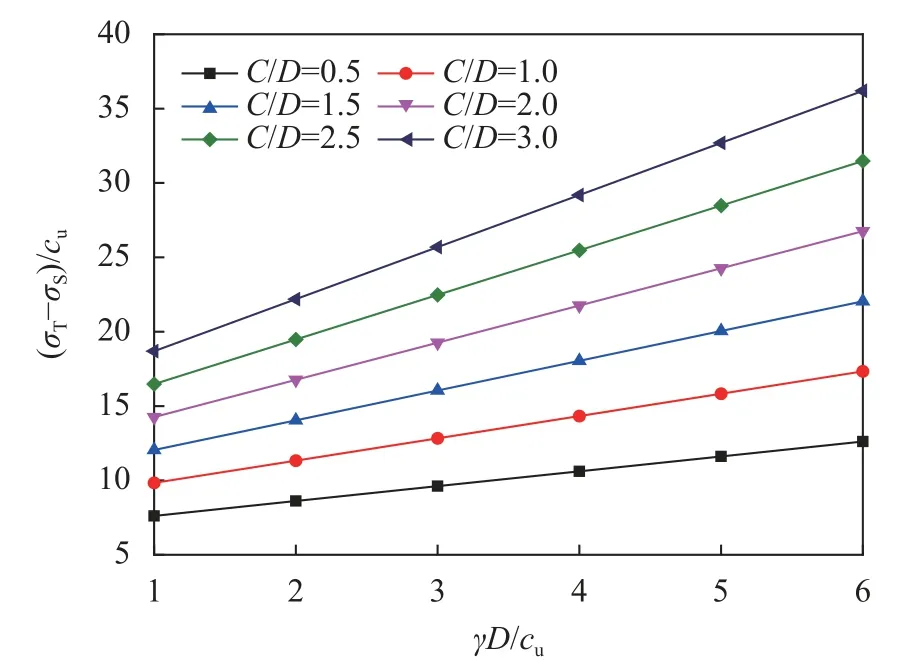
图9 不同C/D 情况下荷载参数(σT-σs)/cu与重度参数γD/cu的关系

4 工程应用与分析

针对盾构隧道的不排水效应分析，本文选取典型案例开展数值模拟。

4.1 计算工况及参数

假定土体的不排水抗剪强度不随深度变化，隧道穿越土层和覆土层都为均质土层，列出3 种不同的工况，各工况的物理力学参数见表1。其中，隧道直径取6 m，保持水位线始终位于地表，地表超载假设为零。

表1 不排水条件数值模拟的物理力学参数

4.2 结果对比分析

（1）均质土情况（工况1）

将本文提出的不排水理论解析解与三维数值模拟解进行对比，结果如表2 所示。可以看出，当隧道埋深较浅（C/D＜1）时，理论解析得到的上限解与三维数值模拟解比较接近。随着隧道埋深比C/D的增大，理论解析解与数值模拟解的差距逐渐变大。

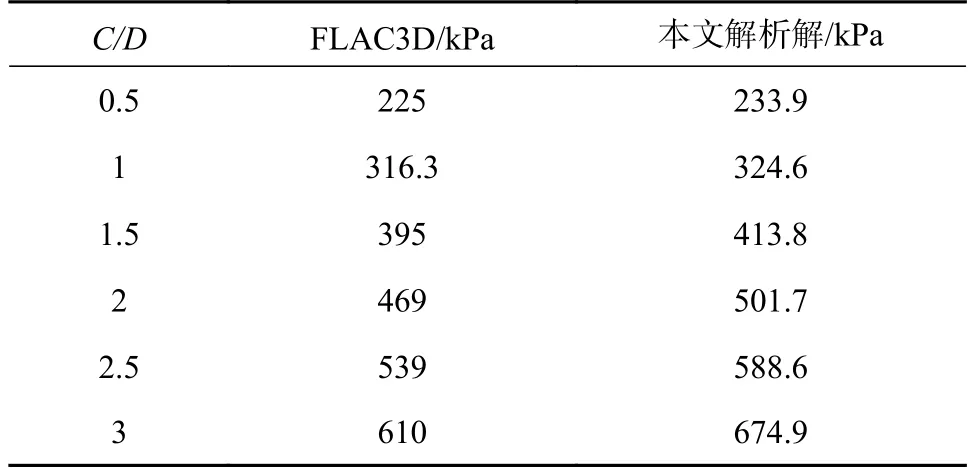
表2 不同埋深比情况下解析解与数值解的对比

工况2 和工况3 对应的成层土极限支护力解析解与数值解的对比如表3 示。可以看到，对于非均质地层且覆土层为均一地层的情况，本文提出的模型得到的极限支护力解析解与数值解的结果偏差均在可接受的范围，能够较好吻合。

表3 成层土解析解与数值解对比

成层土两种工况下的开挖面前方破坏区位移云图如图10 所示，可以看出，工况2 和工况3 的破坏区都发展到了地表，且上部破坏区的边界是近似竖直的。值得注意的是，虽然本文采用了整体失稳模型分析不排水条件下的盾构开挖面被动稳定性，工况2和工况3 在开挖面上的破坏区也出现了局部失稳现象，尤其是工况2 更加明显，这可能是因为工况2 覆土层的不排水抗剪强度小于穿越层，而工况3 覆土层的不排水抗剪强度大于穿越层。

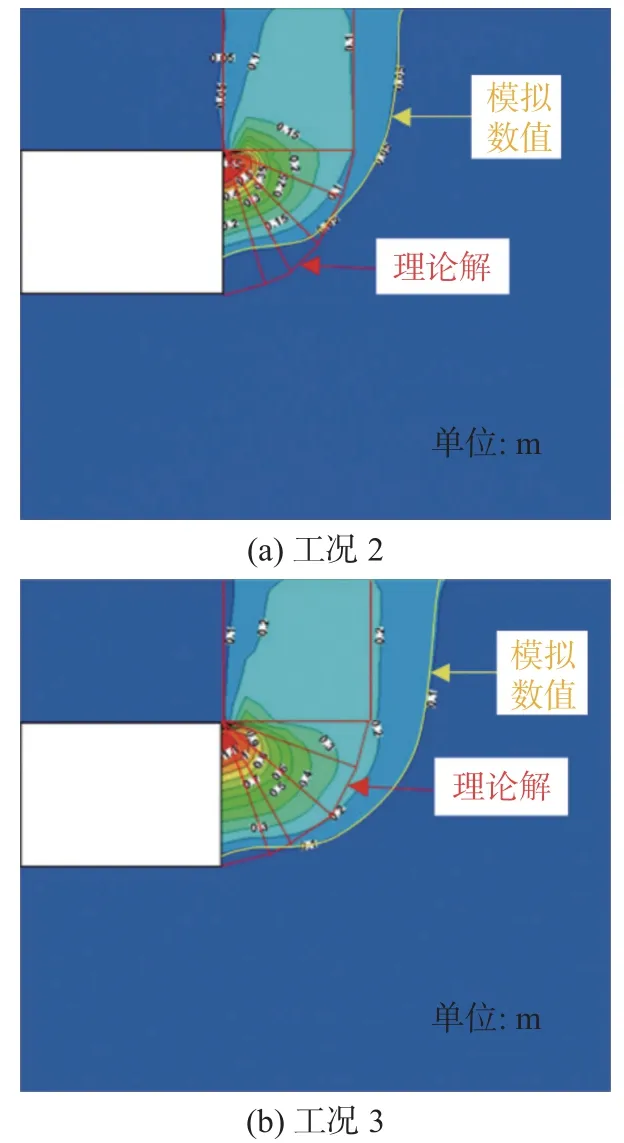
图10 成层土情况下的破坏区位移云图

5 结论

（1）针对不排水地层，提出了可以快捷估算均质土层不排水条件下盾构隧道开挖面被动破坏时的极限支护力的计算公式。

（3）采用提出的模型分别针对均质土和均一覆土层的成层土两种情况进行计算，将得到的解析解与数值模拟得到的数值解进行对比，结果表明，本文提出的破坏模式具有一定的合理性和适用性。