基于阀门隔离区域的供水管网管道故障韧性评价模型

康引引,杨 坤,刘 俊,宋朝阳

(1.燕山大学建筑工程与力学学院,河北秦皇岛 066004;2.上海城市水资源开发利用国家工程中心有限公司,上海 200082;3.燕山大学河北省建筑低碳清洁供热技术创新中心,河北秦皇岛 066004)

随着供水管道的腐蚀老化、人为损坏或地震等自然灾害的影响,管道不可避免会发生破裂而失效,导致供水服务中断。为了提高供水服务的连续性,供水企业需要定期更新维护老旧管道,在资金有限的情况下必须优先维护重要的管道。此时,需要分析管道在失效时的后果,为管网更新维护提供决策支持,提高供水企业的资产管理水平。

管道事故评价以管道失效隔离后供水服务的降低程度作为指标,评价管道的重要性[1]。管道失效后需要关闭周边的阀门,形成隔离区。除了隔离区停水,其他区域也会由于低压影响正常用水。以水力模拟进行事故评价需要采用压力驱动模拟方法[2-4]。也有研究[5-6]根据阀门隔离区域,只分析隔离区的缺水量进行事故评价。除了基于水力性能的重要性分析,还包括拓扑指标的管道重要性评价[7-8]。目前的管道失效分析大多数只考虑管道隔离后供水服务下降的影响,未考虑维修后服务水平恢复的变化。而恢复能力直接影响供水服务能力,韧性能够描述供水管道从失效到恢复的全过程,因此,将韧性纳入供水管网状态评价中具有重要的现实意义。基于此,美国2018年《水务基础设施法案》要求从2020年开始,所有服务人口大于3 300人的供水系统均需要进行韧性评估[9]。市政基础设施系统的韧性设计,应兼具结构上的灵活性和对空间的刚性管控[10]。

本文考虑实际阀门位置,采用图论算法建立阀门隔离区域图。根据隔离区域图布置阀门,尽量避免隔离一个区域时,其他区域与水源意外隔离而停水的情况[11]。根据韧性理论分析多种事故工况时,供水管网事故-隔离-恢复的全过程根据压力驱动模拟方法,统计隔离区和受影响区的缺水量,评估隔离区的重要性,分析关键隔离区域。

1 韧性分析框架

1.1 韧性定义

供水管网韧性是指供水管网抵御、吸收灾害影响,恢复正常供水,并适应未来环境和不确定性扰动引起的变化的能力[8],具有抵御、吸收、恢复和适应4个阶段[12],其中恢复性是韧性区别于其他性能指标的本质特征。韧性一般通过韧性曲线描述,如图1所示,其中横坐标为时间,纵坐标为管网性能参数。t0～t1时,系统处于正常状态,系统可抵御各种扰动而保持正常供水;t1时刻发生破坏,在t2时刻达到最大破坏程度,t1～t2时,管网吸收破坏的影响,性能下降;t2之后开始逐渐恢复,直到t3时刻管网恢复到稳定状态;t3之后,系统从事故中积累经验,进行针对性的更新维护等,以适应未来的不确定性。

图1 供水管网韧性曲线

基于上述韧性理论,Diao等[13]提出整体韧性分析方法对爆管、火灾流量和水质污染3种故障模式进行了韧性评价。Meng等[14]考虑了管道失效时间和恢复时间对韧性的影响。上述研究未讨论不同阀门布置情况对韧性的影响。

1.2 韧性评价指标

韧性用于评价供水管网面对灾害时性能的变化,因此,各种水力、水质等性能评价指标都可用于韧性分析。本文以管道失效隔离后供水满足率和不满足率2个水力指标评价管网韧性,模拟从管道破坏到隔离、恢复全过程的韧性变化。特别考虑了不同阀门密度情况下系统供水量满足率的变化,分析了阀门隔离对停水区域和低压影响区域系统供水不满足率的影响。

如图1所示,如果以供水量满足率为系统性能评价指标,管网正常运行时供水量满足率为100%。在事故发生后供水量满足率下降,最终经维修重新恢复到100%。t1～t3韧性曲线下方的面积大小反映系统韧性的高低,面积越大,故障时系统性能损失越少,系统韧性越高。系统韧性(R)可表示为式(1)。

R=A/E

(1)

其中:A——t1～t3时管道故障时系统韧性曲线下方面积,m2,其值大小表示事故时管网韧性的高低;

E——t1～t3时系统正常状态时供水量满足率保持100%的直线下方的面积,m2。

而韧性曲线上方的面积反映韧性损失,则系统韧性损失(L)为式(2)。

L=(E-A)/E=1-R

(2)

假定t时刻系统处于正常状态,其用水量为式(3)。

(3)

其中:j——节点编号;

N——供水系统的节点总数量,个;

当t时刻管道故障处于隔离状态时,部分节点由于低压或停水,系统实际用水量要低于正常时用水量,则系统实际用水量为式(4)。

(4)

t时刻系统供水量满足率(RSt)可计算如式(5)。

(5)

t时刻系统供水不满足率(RLt)计算如式(6)。

(6)

则整个故障期间供水系统不满足率(RL)计算如式(7)。

(7)

其中:t——模拟故障时刻,s;

T——系统恢复正常时刻,s。

供水系统不满足率即为韧性的损失,其中包括失效管道隔离区域内所有停水节点缺水量和隔离区域外受低压影响的其他节点缺水量。其中,被隔离区域i(I)韧性损失量(RLI)计算如式(8)。

(8)

受影响区域j(I)韧性的损失量(RLP)计算如式(9)。

(9)

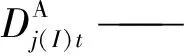
2 隔离区域识别

供水管道故障后为了及时维修,需要关闭周边阀门,切断破坏管段和周围管段的联系。隔离区域可以通过阀门区域图(segment-valve graph,SVG)来确定。图2(a)为简单供水管网,在用水节点附近添加虚拟节点和短管道模拟阀门设置,开启、关闭短管道模拟阀门开闭,可以准确分析阀门布置、阀门区域与系统性能的关系。

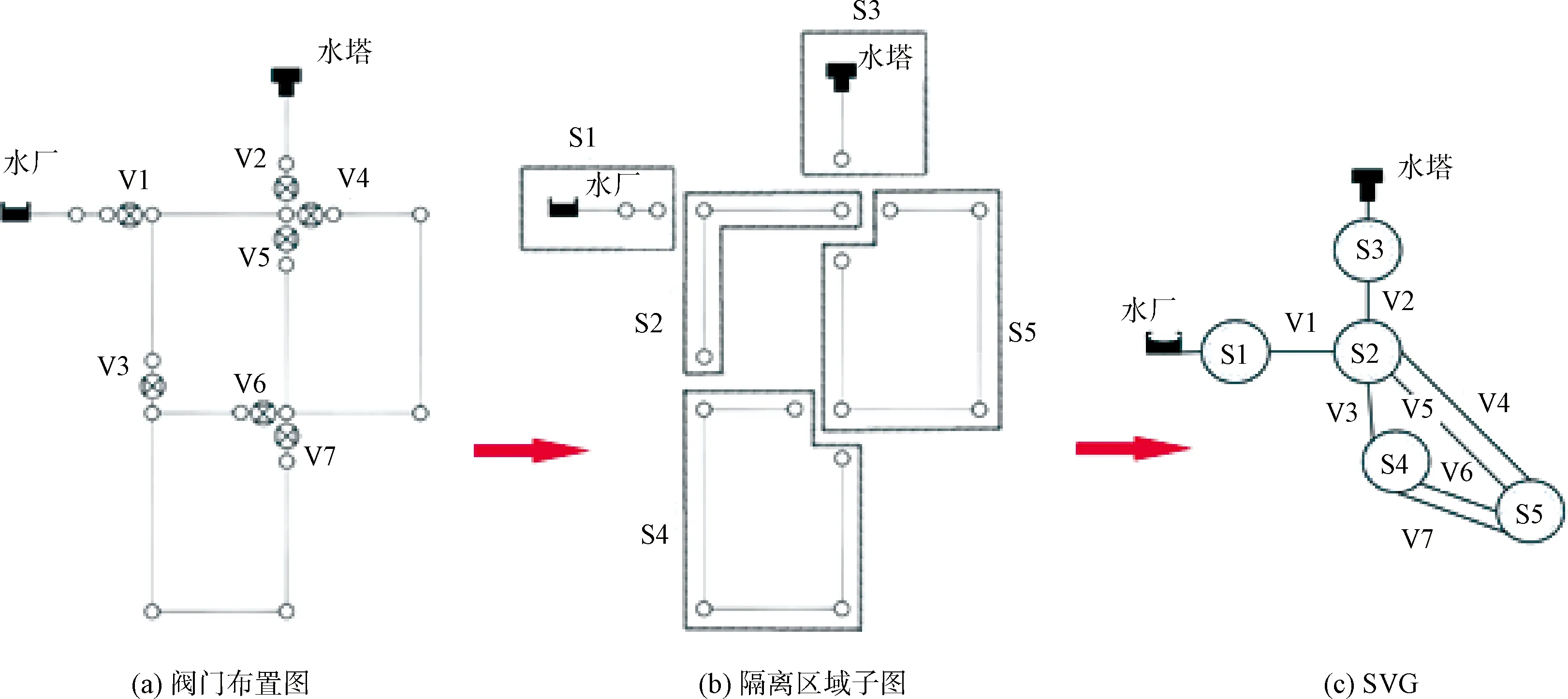
图2 简单管网阀门拓扑图

如图2(b)所示,将隔离阀从管网图中删除以后,会产生许多连通子图,子图间边界即隔离阀。通过宽度优先搜索算法,可以遍历获取所有连通子图。通过遍历查找隔离阀两节点所在子图,即可找到隔离阀连接的子图。以子图为节点,隔离阀为连接,可生成阀门隔离区域图,如图2(c)所示。SVG图可以清楚显示不同隔离区域间连接关系,为后续故障区域阀门关闭操作提供指导。

3 应用与分析

以EPANET2中Net3管网为例进行供水管网韧性分析。Net3管网共有91个节点,115个管段,2个水源,3个水塔,2个水泵。基于WNTR压力驱动水力模拟进行爆管分析,压力驱动水力模拟采用Wagner公式[15],其中压力指数为0.5,最小出流压力为0,正常供水最低压力为20 m,延时水力模拟步长为1 h。

3.1 阀门密度对韧性的影响分析

《室外给水设计标准》(GB 50013—2018)[16]规定输水管应考虑自身检修和事故时维修所需要设置的阀门;根据消防的要求,配水管网上两个阀门之间消火栓数量不宜超过5个。《城镇供水管网运行、维护及安全技术规程》(CJJ 207—2013)[17]规定,当发生爆管、破损等突发事件时,应迅速关阀止水,组织应急抢修。由此可见,在供水管网运行维护、事故抢修等需要关闭阀门时,为了降低对供水服务的影响,必须达到一定的阀门密度。Walski等[18]表示,为了最大限度地减少对整个系统和区域用户服务的影响,需要更高密度的隔离阀,阀门密度越高,管段破坏后隔离措施对供水管网系统韧性的影响就越小,但阀门成本在很大程度上限制了阀门数量。因此,必须合理优化供水管网阀门布置,减少阀门隔离区域对管网系统性能的影响。

本文采用阀门比(RV)衡量阀门密度,RV的值在0～1,可用于阀门密度的比较,如式(10)。

(10)

其中:v——阀门数量,个;

m——管道数量,条,如果每个管道两端均安装阀门,则最多可安装阀门数量为2m。

本文分析了不同阀门密度下4种阀门布置情况:方案一为2N个阀门布置原则,即在每个管道两节点处均布置阀门[图3(a)],RV=100%;方案二为N个阀门布置原则,指的是平均每个管道上安装一个阀门[图3(b)],RV=50%;在实际供水管网中由于成本约束,阀门比较小,为此采用RV=18.3%(42个阀门)的有限阀门情况,并分为随机布置和优化布置两种情况;方案三为有限阀门布置时随机确定阀门的位置[图3(c)];方案四为有限阀门布置时借助SVG优化后的阀门位置[图3(d)]。

图3 4种阀门布置方案

对于管道故障为对象的供水系统整体韧性分析,需要确定各种故障方案,如单根管道故障、多根管道同时故障和所有管道同时故障。对于单根管道故障,所需要分析的故障方案数量为管道数量,此时故障强度低,管网韧性能力较强,而所有管道同时发生故障则对应唯一故障方案,此时故障强度最大,系统完全丧失韧性。对于多根管道同时故障,随着同时发生故障的管道数量增多,故障强度增大,为了进行韧性分析,需要确定各种可能的故障方案组合,目前普遍采用的是随机采样确定故障方案,该故障采样方案可能会丢失一些重要的故障方案而影响韧性全面评价,此时可进行目标采样作为随机采样方案的补充[13]。本研究采用隔离区域为单元进行管道故障分析,旨在模拟分析供水管网从破坏到恢复的全过程,不涉及供水系统整体韧性评价,因此,对于故障方案进行了简化,随机设置14根管道并假定同时发生故障,需要进行隔离、维修,直至恢复,同时假设在9:00发生故障,12:00同时关闭阀门,14:00完成修复并同时开启阀门,总模拟时长为42 h。

经过水力模拟计算,最终得出4种不同阀门布设情况下系统韧性曲线,如图4所示。显然,随着阀门数量的减少,故障期间系统供水量满足率越低,韧性损失越多,系统韧性越小。具体来说,以方案一为基准,方案二阀门数量减少50%,韧性损失增加0.24%;方案三阀门减少81.7%,韧性损失增加0.89%,如表1所示。

表1 4种隔离阀布设方案对比

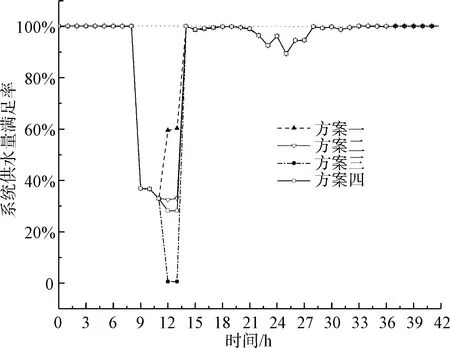
图4 4种阀门方案下供水管网韧性

方案三与方案四的阀门区域拓扑结构如图5所示。方案三隔离区域有24个,方案四的隔离区域有26个。方案三有45.8%的隔离区域为末端区域,上游区域隔离时会使其意外隔离,例如图5(a)中区域4、13和14,其上游区域为12,当区域12内管道故障进行隔离时,会使得下游的4、13和14与水源断开而意外停水。相比方案三,优化后的方案四末端区域占比下降到26.9%,大大降低了上游故障隔离导致下游意外停水的情况。以方案三与方案四为例对比分析了相同阀门密度下不同阀门布置方案的系统韧性变化。同样可以看到,通过优化阀门位置后,故障管道时所需关闭的阀门数量有所减少,同时系统在故障时韧性有显著提升,相比于方案三,方案四韧性提升约12%。由此可见,当考虑管网实际情况,阀门数量远远小于理想情况时,合理的阀门优化可在不显著降低韧性的基础上大大降低阀门数量,节约阀门安装成本。

图5 42个阀门情况下的阀门区域

另外,由图4可知,不管哪种阀门方案,故障完全修复后,系统在21～28 h内仍出现供水不满足的情况。其主要原因是故障修复后,水塔3大量进水,水厂2出水管压力骤降,导致下游区域出现低压供水。通过减小水塔进水管道直径降低水塔补水量或增大水厂出水管道直径,可以消除这种低压波动现象。由此可见,不同隔离区间存在水力相关性,某一区域故障或工况变化会影响系统其他区域。

3.2 区域韧性分析

以方案四的管网阀门分布为对象,当每个隔离区域发生管道爆管后,关闭周边阀门形成隔离区域进行维修,分析隔离直到修复完成恢复正常供水的韧性变化。除爆管外,爆管后的应急响应也是影响系统韧性的主要因素之一,主要包括爆管识别、爆管定位、区域隔离以及维修工作。上述工作受到爆管强度、爆管位置、爆管识别和定位技术、应急维修保障能力等的影响,所需时间需要根据实际情况而定。2018年WDSA-CCWI国际会议举办的灾后响应和恢复的竞赛中给出了阀门关闭、管道修复和更换时间[19]:关闭一个阀门的时间为15 min;管道修复和更换时间主要与管径有关,DN100～DN1000的管道修复和更换时间分别为3～12 h和4～22 h。本文区域韧性分析中假定只有一根管道发生爆管并进行隔离维修,爆管识别、定位和关闭阀门的时间为3 h,管道修复时间为12 h。对于本文案例管网,假设爆管发生在9:00,工作人员在管道破坏发生后立刻到达现场,在12:00关闭隔离进行维修,且假定维修资源充足,在24:00完成维修工作,恢复通水。总模拟时长为48 h。

将破坏管段所在区域隔离后,位于隔离区域内的用户,便无法得到供水服务。此时管网的拓扑结构也会发生了改变,处于隔离区域上下游的用户,也会受到影响,导致部分低压供水。依次对每个阀门区域进行爆管韧性分析,不同区域隔离的韧性降低程度如图6所示,包括隔离停水区域韧性损失、低压供水区域的韧性损失以及整体韧性损失。

图6 区域韧性分析

根据韧性损失的影响,韧性损失在[0.04,0.20]为三级隔离区域,(0.2,0.5]为二级隔离区域,(0.5,1.0]为一级隔离区域,该3个等级共包括10个隔离区域,约占隔离区域总数量的40%,如图7(a)、图7(b)所示。左侧水厂的工作时间仅在01:00～14:00,且供水量小,上方水厂为主力水厂,因此,管网的重要区域主要集中在上方水厂到下游区域22的主线上。

图7 供水管网区域韧性等级

对韧性影响最大的3个区域(7、13、19)进一步分析其韧性变化,每个区域韧性损失如表2所示,韧性变化如图8所示。区域韧性具体分析如下。

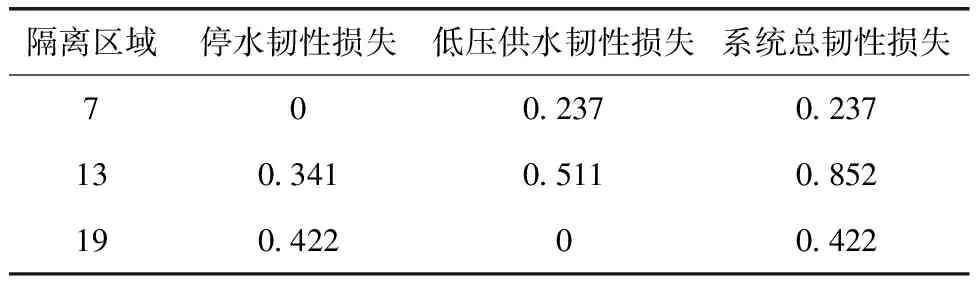
表2 3个阀门区域隔离时韧性损失

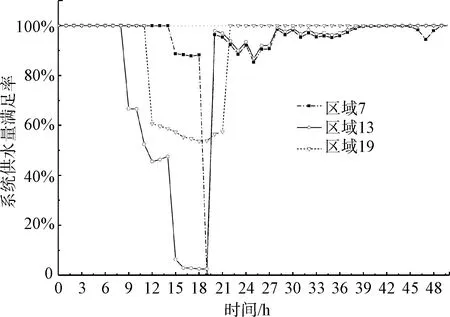
图8 重要区域隔离情况下供水管网韧性

(1)区域13对管网韧性的综合影响最大,图8中在该区域发生破坏但未被隔离前,管网性能有很大程度的下降,并且该区域从隔离到恢复后,系统也仍存在大范围供水不足情况。这意味着当该区域遭到破坏后,对自身和其他区域都会带来严重的损失。其原因是该区域在两个水源主要供水路径上,且区域内用水量较大,该区域故障会导致本区域停水,停水韧性损失为0.341,其下游区域也会受到严重的低压影响而缺水,低压导致韧性损失为0.511。因此,在日常运维中需要对区域13着重管理,达到增强管网系统的韧性的目的。

(2)区域位置和拓扑结构是影响管网其他区域的两个重要因素。如区域7,从破坏到隔离恢复持续时间极短,但后续影响持续时间较长,表明虽然自身流量很小,但位置接近水源,处于主要供水路径上,因此对其他区域影响显著,使得其他区域韧性损失达0.237;区域15、16和17同样自身流量很小,但拓扑结构复杂,仍然对其他管网产生很大影响。可对该区域采取早隔离、早维修的方式,有利于降低对系统韧性的影响。

(3)流量大的区域不一定对其他区域产生影响,例如区域19,供水不足现象只发生在破坏到隔离期间,隔离后管网性能立即得到恢复。原因是该区域存在大用户,但处于供水末端,对其他区域几乎不造成影响,只有本区域停水导致韧性损失,如表2所示。可考虑建设高位水池、增加连通管道等方式提高该区域韧性。

4 结论

(1)提出阀门建模方法,采用图论算法生成SVG,相比于阀门节点连接图,SVG以区域为单元,更方便查看、比较及分析阀门隔离区域对系统韧性的影响。采用图论算法确定SVG,可以获得每个区域的阀门集合。

(2)提出了实际阀门布置下的供水管网管道失效韧性评价框架,涵盖了供水管网从破坏前到复原的4个韧性阶段,提出了基于水力性能的韧性评价指标,可对供水管网事故下韧性进行分析。

(3)阀门密度影响供水管网韧性,在不显著降低供水管网韧性的同时,通过优化阀门可减小阀门密度和安装成本,提高阀门区域连通性。

(4)基于管网韧性评价,对隔离区域进行了重要性评估。结论表明,对管网韧性造成显著影响的除了水量大、处于主要供水路径上的区域外,管网拓扑结构也是影响韧性的重要因素之一。

(5)在未来研究中,应考虑将拓扑结构、水质、经济成本、恢复时间、水安全等作为韧性指标,对供水管网进行全方面韧性评估。同时,应考虑采用智能优化算法进一步优化阀门布置。