一种改进的公路岩质隧道围岩分级方法

王坛华

（福建省交通规划设计院有限公司，福建 福州 350004）

工程岩体分级是岩体工程最重要的课题之一。伴随工程建设发展，两百年来，岩体分级理论不断更新发展，先后产生近百种分级方法［1-4］。国外较为著名的岩体分级有普罗拖吉亚柯诺夫分级（普式分级）（1926）、太沙基分级（1946）、迪尔RQD 分级（1969）、巴顿岩体质量Q分级（1974）、宾尼亚斯基RMR 分级（1973）、印度索隆尔隧洞R分级（1982）、日本国铁弹性波分级等。这些分级方法考虑的参数各有侧重，共十几种，参数有定量、定性、半定量类型。参数的多样性也从侧面反映了工程岩体分级的复杂性。

当前，我国公路隧道围岩分级主要依据《公路隧道设计规范 第一册 土建工程》（JTG 3370.1—2018）［5］（以下简称隧道规范），其基本延续2004版规范的规定，仅对岩体基本质量指标BQ 值计算公式作了微调，以保持和《工程岩体分级标准》（GB/T 50218—2014）一致。一方面，《工程岩体分级标准》作为一个通用性的全国标准，面对丰富复杂的隧道围岩地质情况，其分级计算参数取值存在不少问题，难以完全满足公路隧道围岩分级的要求，在实际应用中引起不少争议和困惑［6-9］。且近年来，山岭重丘隧道深孔地质钻探成本急剧增高，地质钻探的高投入低产出已为技术人员所诟病，工程界亟需一种能降低成本提高效率，同时可确保成果精度的围岩分级方法。另一方面，我国现有对围岩分级方法的研究［10-12］或探测深度不足，或应用范围小，或可操作性差。电阻率法是勘察设计阶段被广泛应用的隧道物探方法，它可挖掘电阻率法成果的应用价值，降低钻探投入，提高工作效率。但目前我国相关研究中，基于电阻率以判定围岩级别的方法尚鲜有报道。为此，笔者在工程实践的基础上，提出一种利用电阻率参数调整系数改进围岩分级的方法，建立改进的BQ 值计算公式，并进行工程应用。

1 现行围岩分级方法及其存在的主要问题

1.1 现行规范中的围岩分级方法

目前的隧道规范围岩分级计算中，岩质围岩基本质量指标BQ及岩体修正质量指标［BQ］的计算公式为

式（1）～（2）中：Rc为岩石饱和抗压强度；Kv为岩体完整性系数；K1为地下水影响修正系数；K2为主要软弱结构面产状影响修正系数；K3为初始应力状态影响修正系数。

公式（1）的使用有2 个约束条件，即：1）当Rc＞90Kv+30 时，Rc取值均为90Kv+30；2）当Kv＞0.04Rc+0.4 时，Kv取值均为0.04Rc+0.4。条件1）表明，当岩石的抗压强度足够大时，完整性系数起主要控制作用；条件2）表明，当岩体足够完整时，岩石抗压强度起控制作用。

隧道规范根据地下水的出水状态，并考虑不同BQ 值围岩抵抗地下水弱化能力的不同对K1取值。即在相同的地下水状态下，BQ越小，K1取值越大，K1介于0～1之间。

主要软弱结构面及其与洞轴线方向组合关系不同，对岩体稳定性的影响就不同。隧道规范给出的主要软弱结构面产状影响修正系数K2［5］92如表1所示。

表1 主要软弱结构面产状下的修正系数Table 1 Correction coefficient for the influence of the occurrence of main weak structural planes

规范同时说明，表1中K2取值适用于1组起控制作用的结构面，不适用于2组及以上结构面。

通常情况下，地应力是个隐性因素，仅当与之相关的工程灾害或表象发生时，才被人们认识到。规范考虑了极高和高初始应力状态，同时结合BQ 值高低给定不同的修正系数取值K3，K3介于0.5～1.5之间。不同初始应力状态下的修正系数K3［5］92如表2所示。

表2 不同初始应力状态下的修正系数Table 2 Correction coefficient for the influence of initial stress state

规范规定，通过开挖产生的岩爆、剥离等现象及围岩强度应力比来判定围岩是否处于极高或高地应力状态。

以上3个修正系数对围岩级别的影响之和最高可达200以上，即经过修正后的的［BQ］值最大可降低2个级别，这说明修正因素的影响不可忽视，其重要性不亚于岩石强度和岩体完整性。

1.2 围岩分级计算参数存在的问题

1.2.1 未考虑层状岩体Rc取值的差异隧道规范以岩石饱和抗压强度Rc作为表征强度。岩石饱和抗压强度与岩石矿物组成、结构构造、隐形结构面、风化程度等相关。笔者在厦沙高速德化段勘察设计阶段，对多个变质岩试样抗压强度成果进行分析后发现，同一地层的微风化云母石英片岩的抗压强度差异可达近5倍（23～113 MPa）。进一步分析岩块片理结构和试验破坏特征，并结合摩尔库伦破坏准则发现，造成这种现象的主要原因是：勘察阶段采用钻孔内取芯，再将岩芯加工成抗压试验试样，片理面是天然的隐性薄弱面，当沿岩芯轴向施加荷载时，在单轴抗压条件下，片理面会最先发生滑移、劈裂破坏，此时片理产状一般介于（45-φ/2）°～（45+φ/2）°，具体如图1所示。可见，在片状或层状岩体钻探中，不易取得合适的岩芯试样，若发现试样片理面或层理倾角不满足要求时，需通过其他手段进行取样。

图1 层状岩石试样单轴受压沿层面优先破坏倾角范围Fig.1 Range of preferred failure angle along the bedding plane of layered rock samples under uniaxial compression

1.2.2 采用岩体声波探测技术测定Kv值具有一定的缺陷

岩体的完整性与结构面的几何特征、性质有关，受结构面的密度、组数、张开度、填充等影响。表征岩体完整性的性质指标有岩体完整性系数Kv、岩石质量系数RQD、岩体体积节理数Jv、节理平均间距等。孔内声波探测技术具有技术先进、操作简便的特点，已经成为测定Kv值最常见的方法。该方法直接利用钻探孔下入声波探头，按0.2～1.0 m每点间距逐段测得Vpm值，Kv计算式为

式（3）中：Vpm为实测岩体声波值；Vpr为不含明显结构面的岩块声波速度。

采用岩体声波探测技术测定Kv值虽然具有较好的便捷性，但此方法亦有一定的缺陷。图2为相同间距不同倾角的两组结构面与钻孔相交的结构面数量对比情况。其中，图2（b）与钻孔相交的结构面数量多于图2（a），故图2（b）经声波测试所得完整性系数小于图2（a）。而实际上，双方的完整性相同。因此，在进行声波成果解译时，要考虑结构面产状因素，避免单纯依赖实测数据。

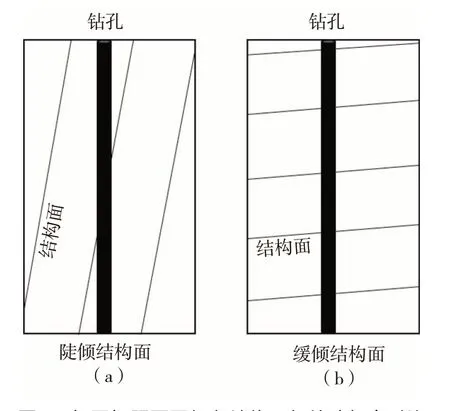
图2 相同间距不同倾角结构面与钻孔相交对比Fig.2 Comparison of intersection between structural planes with the same spacing and different inclination angles and drilling holes

1.2.3K1的确定受主观性影响较大

隧道规范根据地下水出水状态并结合岩体质量指标BQ 来给定地下水影响修正系数K1，根据地下水压力或单位出水量的大小来判定出水状态。规范的考虑有其合理性，但在勘察设计阶段，由于地下水压力和单位出水量很难测定或者测定准确率低，所以，地下水影响修正系数常常凭工程技术人员的经验来确定，主观性很大。

1.2.4K2的取值具有一定的盲目性

隧道规范根据主要软弱结构面与洞轴线的夹角大小及结构面倾角大小给定K2值，目前仅考虑1组结构面的情况，未考虑结构面与洞身相交位置的差异情况。而岩体中存在各种不同成因的结构面，如成岩裂隙、构造裂隙、卸荷裂隙、风化裂隙、岩性接触面等。地质断层面是一种较普遍的主要软弱结构面，对沉积岩和变质岩而言，层理面和片理面对围岩的弱化也起主要的控制作用。主要软弱结构面以外的各类结构面对围岩分级的影响可以在完整性系数Kv中体现出来。

隧道洞身开挖表明，主要软弱结构面对洞身围岩稳定性的影响不仅与结构面产状有关，而且受其他裂隙与主要软弱结构面的组合关系，以及主要软弱结构面与洞身相交位置的影响，不同位置不同组合结构面对隧道围岩稳定性的影响具体如图3所示。根据块体组合稳定性分析理论，当仅存在主要结构面时（如图3（a）），主要结构面对围岩稳定性影响并不大；当存在易于失稳的不利块体组合时（如图3（b）、（c）），围岩稳定性骤降。

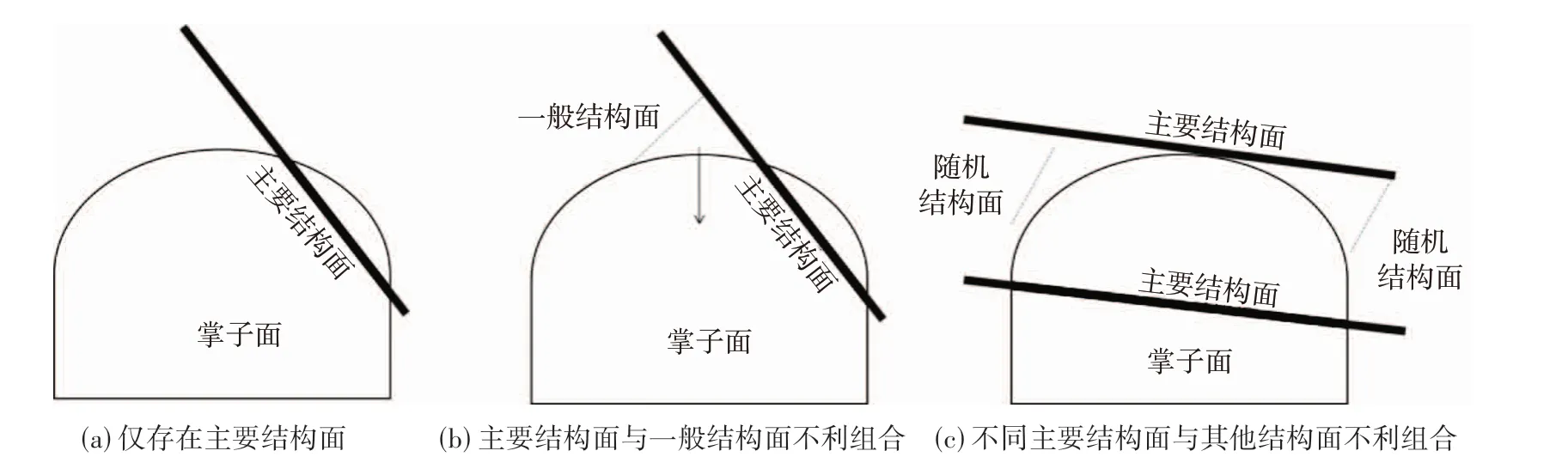
图3 不同位置不同组合结构面对隧道围岩稳定性影响Fig.3 Influence of structures of different positions and combinations on the stability of tunnel surrounding rock

受限于现有勘察技术手段，在勘察设计阶段无法将洞身一般结构面查清楚，主要软弱结构面产状在洞身位置也很难确定，因此，K2的取值也存在盲目性。

2 围岩分级方法的改进

2.1 注重地质背景分析

隧道工程赋存于一定的地质环境，是一种典型的地质工程，受地形地貌、地层岩性、地质构造、水文地质等条件影响。现有BQ 计算式虽然已体现岩石强度、岩体完整性及主要环境要素，但由于地质工程的复杂性，现有量化评价指标难以全面考虑围岩地质条件，存在不足之处，因此，在围岩分级中不能只强调定量评价而轻视定性评价。工程实践表明，隧道围岩分级高度依赖工程经验和工程类比，要注重地区经验积累和地质背景分析，抓住地质构造、地层岩性、地下水、埋深等几个主要因素，从宏观层面判定围岩优劣，并以此作为围岩定量分析结果合理性的校验手段。

2.2 合理确定参数及修正系数的取值范围

参数和修正系数决定了［BQ］的大小。根据以上分析，在不改变围岩BQ 和［BQ］计算公式基本结构的前提下，本研究对岩质围岩参数和修正系数取值作了如下改进。

1）岩石饱和抗压强度Rc。对试验结果逐个分析其偏差率，偏差率=（试验值-平均值）/平均值，偏差率绝对值大于30%的不予统计。层状岩体取样与块状岩体不同，层状岩体应选取缓倾角试样，倾角以不超过25°为宜。

2）岩体完整性系数Kv。声波测孔要结合钻探成果解译，特别要注意钻探岩芯完整性、结构面倾角、钻探过程卡钻位置、漏水或涌水位置等。层状岩体可考虑岩层产状后进行折减，倾角越大折减越多。由于地下水发育程度与岩体完整性关联较大，而地下水在电法勘探成果中的反映也最为明显，因此，结合物探电阻率测深成果引入调整系数λ对完整性系数Kv进行调整。λ介于0～1间。

3）地下水影响修正系数K1。地下水丰富程度与断层带富水性密切相关，在电法勘探成果剖面上，电阻率对地下水反映最为敏感。为此，引入调整后修正系数Kλ1代替K1，当有实测涌水量数据时采用K1，无涌水量数据时采用Kλ1。Kλ1介于0～1间。

4）主要软弱结构面产状影响修正系数K2。在勘察设计阶段，由于随机性结构面发育情况无法确定，主要软弱结构面发育位置和影响也很难评估，因此建议仍保留规范取值方式。但在围岩施工开挖阶段，宜对主要软弱结构及其组合对围岩稳定性的影响加以直接调查，按实际影响位置和程度确定修正系数。

5）初始应力状态影响修正系数K3。极高和高初始应力已有修正系数，但其他状态下尚无修正系数。结合地应力测量成果，建议当围岩破碎、存在张性构造或低水平地应力时，对K3在0～0.5之间进行取值。

2.3 合理引入物探方法

隧道工程常见的物探方法有高密度电法、大地电磁法、大功率直流电法等，这些方法的测试结果一般以等值线剖面图表示。工程实践表明，高密度电法对埋深100 m以下隧道测试效果较好；大地电磁法在深埋大于100 m以上隧道勘察中的效果较好，其视电阻率解译成果等值线图对富水地层、富水构造带反映敏感；大功率直流电法抗环境干扰能力强。大地电磁法在山岭重丘深埋岩质隧道应用面最广，以此法为例，在进行围岩分级计算时，可分别提取隧道洞身位置各段围岩视电阻率值，按视电阻率值大小及梯度变化趋势，计算各低阻段相对低阻率，并以此作为Kv和K1的调整依据。

2.4 采用动态分级

受现有勘察技术水平限制，在勘察设计阶段准确划分围岩级别难度较大。为满足现有技术条件下围岩分级的精度要求，较可行的是采用动态分级方法，即将勘察设计阶段围岩分级作为预分级，而将施工开挖后的围岩分级作为实分级。如此，可以避免过分依赖勘察阶段围岩分级所造成的过于保守的问题，做到按实支护。施工阶段可实测已开挖围岩结构面，计算Jv，并根据式（4）［3］57-58换算，即

经以上改进调整后，勘察阶段改进的隧道围岩［BQ］计算公式为

考虑使用约束条件时，以λ×Kv代替Kv，以Kλ1代替K1。

施工阶段围岩分级可采用定性和定量评价相结合的方法，［BQ］计算时根据掌子面、拱部及边墙完整性不同分块判定。值得注意的是，Kv由实测Jv换算，主要软弱结构面和地应力影响修正系数可由现场实测获得，此时定量计算和定性分析各自优点得以充分体现。

3 算例分析

厦沙高速某隧道位于戴云山脉西侧，属构造侵蚀低山地貌，呈南北走向，地形起伏较大，隧道最大埋深约350 m，大部分埋深250～300 m。岩性主要为侏罗系南园组凝灰熔岩、熔结凝灰岩等，局部见花岗岩侵入带，隧址区发育7条断层和多段物探低阻带，基岩裂隙水、构造裂隙水发育。洞身围岩以微风化岩为主，为硬质岩。现以K82+000～K82+700 段围岩为例说明改进围岩基本质量指标［BQ］的计算方法。

以20 m 为点距沿隧道轴线布置大地电磁测深测线并采集数据，经室内数据处理解译，排除高压电引起的假异常，并考虑地形效应。在隧道沿线选择代表性位置布置钻孔，钻孔深度钻至隧道设计标高以下5～8 m。大地电磁测深视电阻率等值线图如图4所示。

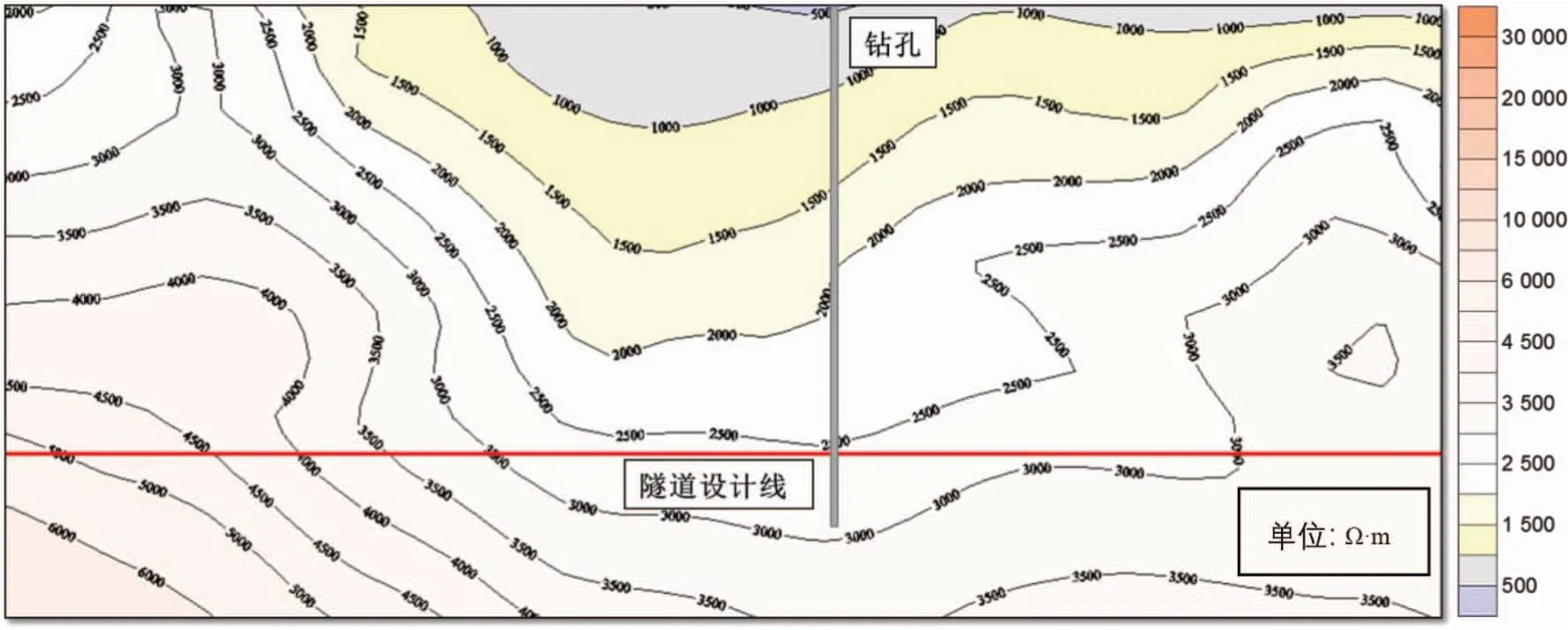
图4 大地电磁测深(EH-4)视电阻率等值线图Fig.4 Contour map of magnetotelluric sounding (EH-4) apparent resistivity

计算过程如下：首先，进行孔内声波测试，获取相应洞身位置的Kv及视电阻率值，由视电阻率值/Kv可获得本段围岩当Kv近似为1时的视电阻率值，即相对完整岩体视电阻率值。将洞身围岩分段视电阻率除以相对完整岩体视电阻率，可求得各段完整性系数调整系数λ。其次，经抽水试验求取实测目标段岩体渗透系数，并结合地区经验和规范对修正系数K1取值，利用各段围岩与实测目标段围岩调整系数λ 的大小比例关系，求得各段围岩调整后地下水影响修正系数值Kλ1。将各参数带入公式（5）即可求得改进的隧道围岩［BQ］值。［BQ］及改进的［BQ］计算结果见表3所示。

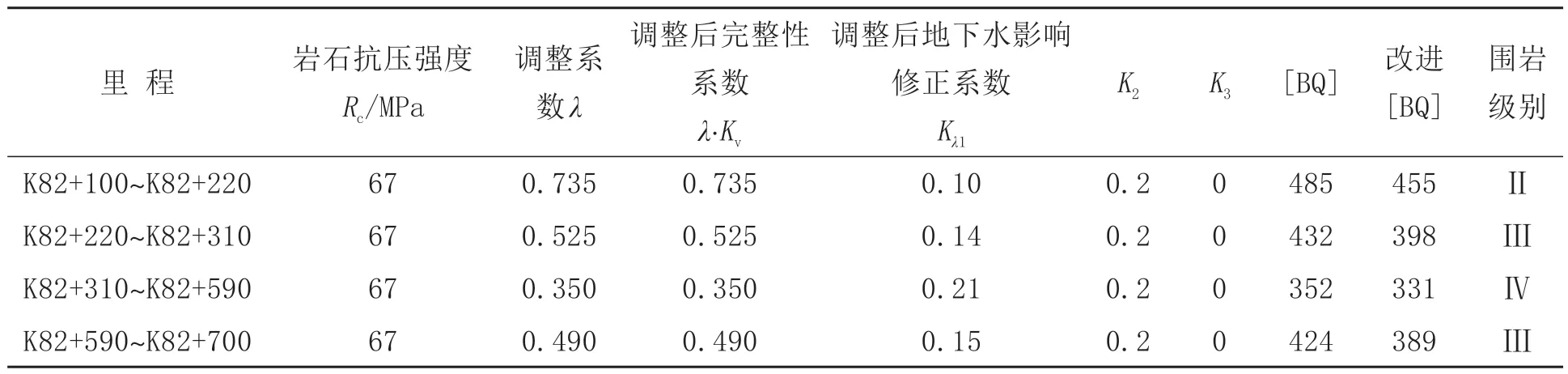
表3 [BQ]及改进的[BQ]计算结果Table 3 Results of [BQ] and improved [BQ] calculation

从表3 可以看出，考虑折减因素的改进［BQ］计算值比未考虑折减因素的［BQ］计算值略低5%～8%，整体偏于安全，与施工揭示的围岩地质条件基本吻合。

4 结论

本文在深入剖析隧道规范围岩分级方法所存问题的基础上，利用隧道物探电阻率值与地下水发育、岩体完整性相关性强的原理，引入调整系数以调整岩体完整性系数和地下水影响修正系数，建立改进［BQ］的围岩级别计算公式，并应用于厦沙高速某隧道围岩分级。算例分析表明，采用本文提出的改进［BQ］计算法可操作性强，［BQ］计算值较之直接计算法降低约5%～8%，与工程实际基本吻合，可实现隧道勘察降本增效。

本文采用的是一种线性折减修正法，主要针对完整性系数和地下水影响修正系数。本方法主要基于地下水富水性与岩体裂隙发育程度呈正相关的原理，且基于同一种岩性电阻率均质假定，当遇干燥的裂隙岩体时本方法不再适用；遇不同岩性的岩体，亦应分段评价。