基于扩散体的声屏障顶部结构的降噪性能
王亚晨, 王巧燕, 邱贤锋
(中海环境科技(上海)股份有限公司, 上海 200135)
0 引 言
随着我国城市交通运输业的不断发展,车流量增大带来的交通噪声污染问题越来越严重,给人们的正常生活带来的不利影响及由此产生的一系列社会问题不容忽视。安装声屏障是控制道路交通噪声的重要手段。目前应用最广泛的声屏障是直立式声屏障。该类型声屏障结构相对单一,降噪效果和防护范围取决于其有效高度,增加屏体高度能提升声屏障的降噪效果和防护范围。设计特殊的声屏障顶部结构是提升声屏障降噪效果的一个重要方式,目前已研制出T型、圆柱型和Y型等多种形式的声屏障顶部结构[1-2]。
声扩散体是根据伪随机扩散理论设计的一种声学结构,具有良好的散射特性和一定的吸声性能,常见的有二次余数序列扩散体(Quadratic Residue Diffuser, QRD)和原根序列扩散体(Primitive Root Diffuser, PRD),在室内声学设计中具有广泛应用,在声屏障领域的研究和应用还处于起步阶段[3-5]。现有的研究通常采用有限元/边界元数值仿真计算方法,结合试验测试进行,研究的内容主要集中在扩散体结构的散射性能或吸声性能上,试验条件多为平面波正向或侧向入射,结构体尚处于理论设计阶段[6-9]。将扩散体结构应用于声屏障中,并检验其降噪性能,是一个重要研究方向。
1 声屏障扩散体顶部结构设计
声学扩散体的基本结构由一系列一维的槽或二维的管道组成,各槽口或管道口共同组成一个声学平面,各槽或管道的深度按一定的伪随机序列排列。根据亥姆霍兹共振原理,该声学平面具有一定的扩散作用和吸声性能。当声波入射到扩散体结构表面时,会均匀地分散在可能的方向上,取得良好的散射特性。二次余数序列是扩散体结构设计中常用的伪随机序列,其计算公式为
Sn=n2mod(N)
(1)
式(1)中:n为整数;N为奇素数;Sn为二次余数序列,表示为n2对N取模之后的最小非负数。二次余数序列关于n=0和n=(N-1)/2对称,并以N为周期。N取不同的奇素数(5~13阶)时对应的Sn见表1。

表1 N取不同的奇素数时对应的Sn
扩散体结构的槽深度序列dn的计算公式为
(2)
式(2)中:fr为设计频率;c为声波在介质中的传播深度。由表1可知,N的阶数越高,Sn序列中的最大值越大,对应的最大槽深也越大。槽深增大有助于向高频扩展扩散体结构的散射性能,同时能使整体结构增大。顶部结构过大不仅会增大其在工程应用中实施的难度,而且会带来安全隐患。综合考虑,认为7阶二次余数序列是合适的选择。
扩散体扩散作用的最大有效波长λmax和最小有效波长λmin的计算公式分别为
(3)
λmin=2w
(4)
式(3)和式(4)中:dmax为扩散体中的最大槽深值;nmax为最大序列数值;w为扩散体槽宽。
由上述计算公式可知,设计频率fr决定了扩散体结构的最大槽深,是扩散作用的最低有效频率。据统计,道路交通噪声的等效频率一般在400~500 Hz[10-11],此次QRD扩散体结构的设计频率取400 Hz。同时,为提升吸声性能并兼顾防护效果和美观,在扩散体结构外侧设计弧形微穿孔护面板。设计的2种声屏障扩散体顶部结构横截面示意图见图1,其中:QRD-1为对称设计,忽略了槽深序列值“0”;QRD-2为非对称设计,具有完整的槽深序列。
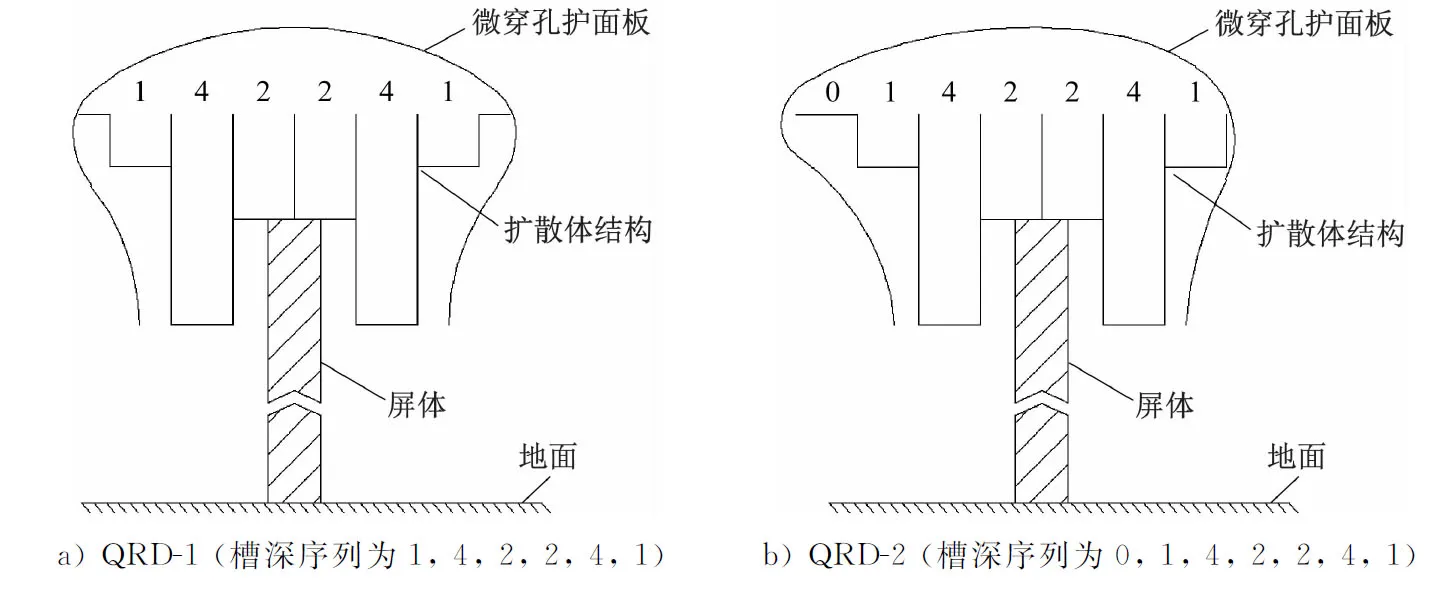
图1 设计的2种声屏障扩散体顶部结构横截面示意图
根据该设计加工完成的声屏障QRD顶部结构足尺模型的工程参数见表2。

表2 声屏障QRD顶部结构足尺模型的工程参数
2 降噪性能仿真计算
采用基于菲涅尔理论的经验公式无法准确计算出声屏障顶部结构对声场的影响,而数值计算法基于声波的波动方程理论,能在复杂结构中取得准确的计算结果。为求解声波入射到声屏障顶部扩散体结构上之后的散射情况和声场分布,采用有限元耦合边界元法(Finite Element Method-Boundary Element Method, FEM-BEM),在顶部结构区域建立有限元模型,保证求解精度满足要求。在计算区域外耦合边界元模型,在计算区域内的计算完成之后,只需通过边界元模型对边界进行离散,即可求解出大尺度范围内的点值[12]。
根据足尺模型的工程参数建立2种QRD结构的FEM-BEM声学模型。为加快计算速度,按以下原则对足尺模型进行简化:
1) 假定足尺模型为无限长的声屏障和线声源,建立二维声学模型;
2) 忽略结构薄板的厚度,用声学边界条件替代;
3) 仿真计算的重点是声屏障的顶部结构,估忽略顶部以下的直立屏体结构,用声学边界条件替代。
声学模型边界条件和计算域参数设置见表3。
分别对2种QRD结构的声学模型(QRD-1和QRD-2)进行建模计算,同时对仅有微穿孔护面板而无内部QRD结构的声屏障(以下简称普通声屏障或Normal)和不设置声屏障的空场地(noBarrier)2种工况进行建模计算,将其作为对比对象,其中普通声屏障的总高度与QRD声屏障的高度一致。声学模型示意图见图2。

图2 声学模型示意图
3 半消声实验室测试
在半消声实验室内安装2种QRD结构声屏障和普通声屏障的足尺模型。声屏障的高度和声源位置与声学模型一致。受实验室内部空间大小的限制,取声屏障的长度为6 m,从实验室一侧壁面的吸声尖劈延伸至另一侧壁面,尽量减少声屏障两侧的绕射,使测试条件接近无限长声屏障的工况。在声屏障一侧的中轴线上放置扬声器,与声屏障之间的水平距离为2 m。扬声器为全频段无指向性声源,可发出100~20 000 Hz频段内的白噪声。
在声屏障另一侧的中轴线上设置不同距离的测点,测试3种声屏障安装前后的噪声值变化。测试重点是验证顶部结构对声波的扩散和降噪效果,测点设置于顶部结构上方1 m处。声源与声屏障顶部结构外侧边缘之间可用一条直线连接,直线上方无声屏障遮挡(声照区),下方存在遮挡(声影区)。测试设备布置示意图见图3;试验现场照片见图4。

图3 测试设备布置示意图
4 仿真计算和结果与分析
4.1 仿真计算结果与分析
以扩散体顶部结构横截面的几何中心为圆心,以1 m为半径设置一条圆截线,计算圆截线上的极坐标声压级值,如图3b所示,其中:0°指向声屏障的正上方;0°~90°为噪声源一侧;-90°~0°为接受点一侧。该声压级反映了声波在声屏障顶部绕射时,散射声场在不同方向的分布情况。计算频率选择扩散体结构的设计频率(400 Hz)和2个倍频程中心频率(250 Hz和500 Hz)。
仅考虑顶部结构上半圆周的散射声场分布情况,不同工况下声屏障顶部结构上方的散射声场分布见图5。
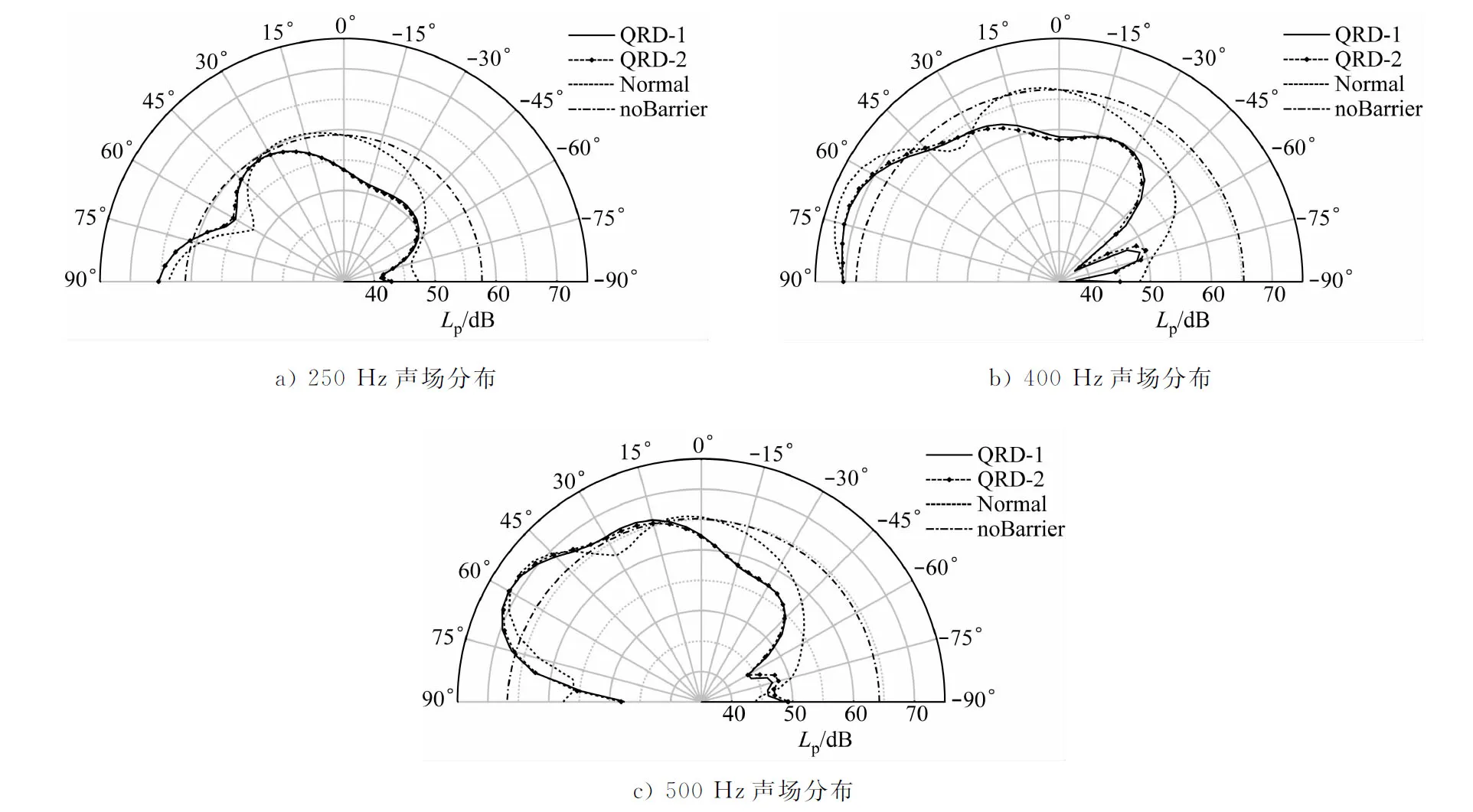
图5 不同工况下声屏障顶部结构上方的散射声场分布
由图5可知:当无声屏障时,声场从90°至-90°方向呈自然衰减的趋势;设置声屏障之后,由于声波在屏体结构表面的反射作用和在屏障顶端的绕射作用,声场分布发生了很大变化。
在30°~90°范围内,2种QRD结构声屏障和普通声屏障的声场大于无声屏障的声场,这是由于屏体结构反射造成声能增强。QRD结构声屏障因具有扩散特性,在声源方向的反射声能大于普通声屏障。在声波传播越过0°角之后,普通声屏障开始出现声场衰减现象,衰减程度从0°至-90°方向逐渐增大。
2种QRD顶部结构在不同频率下的声场分布较为接近,与普通声屏障的声场分布存在很大差异。QRD结构声屏障在15°角时即开始出现显著的声场衰减,在-75°~15°范围内其声场分布显著低于普通声屏障。QRD结构声屏障因具有散射性能,改善了顶部区域的声场分布,使更多的声能向噪声源方向反射,从而减小了绕射声能的大小,提升了声屏障的降噪性能。
用设置声屏障前后相同位置处声场声压级的差值表征插入损失,计算得到2种QRD结构声屏障和普通声屏障在声屏障后方的插入损失(即-90°~0°范围),结果见图6。

c) 500 Hz插入损失分布
由图6可知:2种QRD结构声屏障的插入损失接近,QRD-2型声屏障略优于QRD-1型声屏障,均明显优于普通声屏障。QRD结构声屏障在250 Hz频率下沿-15°和-80°方向有2个显著的插入损失峰值,在扩散体结构设计频率(400 Hz)下的插入损失明显高于在其他频率下的插入损失(在-15°、-60°和-80°方向存在显著的损失峰值),在500 Hz频率下的插入损失峰值出现在-15°和-60°方向。
4.2 半消声实验室测试结果与分析
利用测试结果对仿真计算得到的规律进行验证,测点与声学计算模型的对应位置如图3b所示,测点声压级测试结果见表4。

表4 测点声压级测试结果 单位:dB(A)
由表4可知,N1位于声屏障声照区,设置普通声屏障之后,全频段声压级仅降低0.2 dB,无明显的降噪效果。从分频声压级来看,在500 Hz以下的低频区域,普通声屏障有2 dB左右的降噪效果,但因噪声高频成分的掩蔽,对全频段噪声的降噪效果极为有限。
2种具有扩散体顶部结构的声屏障在测点N1的声压级显著低于普通声屏障。QRD-1型声屏障的全频段声压级降低约2 dB,QRD-2型声屏障的全频段声压级降低约3 dB。从分频声压级来看,QRD-2型声屏障略优于QRD-1型声屏障。与普通声屏障相比,QRD结构声屏障的降噪效果在250 Hz频率下提高了约1 dB,在400 Hz频率下提高了约3 dB,在500 Hz频率下提高了约2 dB。声屏障在扩散体设计频率(400 Hz)下的降噪效果最优。
测点N2位于声屏障的声影区。3种声屏障在全频段声压级和分频声压级下都有10 dB以上的降噪效果,依然呈现QRD-2>QRD-1>普通声屏障的规律。声影区的测点除了顶部绕射衰减,主要降噪贡献量为屏体隔声衰减,故在噪声源较近的情况下3种声屏障的降噪效果差异较小。
试验测试结果与声学仿真计算结果在绝对数值上存在一定的差异,但变化规律具有良好的一致性。QRD顶部结构对入射声能存在扩散作用,能减弱绕射声能,其突出特点是在普通声屏障的声照区产生了2~3 dB的降噪效果,扩大了声影区的范围,提升了声屏障的整体降噪效果。
5 结 语
本文根据声扩散体理论,针对交通噪声的频谱特点设计了2种具有QRD结构的声屏障顶部结构。采用FEM-BEM建立了2种QRD顶部结构声屏障的声学模型,并对其进行了仿真计算,对比了其扩散性能和降噪效果。在半消声实验室内进行了足尺模型现场试验测试。仿真计算结果与试验结果具有良好的一致性。
扩散体顶部结构能有效改善声屏障顶部的散射声场分布,减弱其绕射声能,从而提升声屏障的降噪效果。具有扩散体顶部结构的声屏障在顶端后上方约75°的扇形空间内有显著的增强降噪效果的作用,在设计频率(400 Hz)下的降噪效果最优。与无扩散体结构的声屏障相比,具有扩散体顶部结构的声屏障在非遮蔽区得到了2~3 dB的插入损失提高,在声屏障总高不变的情况下扩大了声影区的范围,在实际工程中具有良好的应用前景。

