排水条件对砂岩力学及其变形局部化特性影响试验研究
许 江 ,曹 琦 ,彭守建 ,陈奕安 ,张倩文 ,饶豪魁
(1.重庆大学 煤矿灾害动力学与控制国家重点实验室, 重庆 400044;2.重庆大学 复杂煤气层瓦斯抽采国家地方联合工程实验室, 重庆 400044)
0 引 言
地下水渗流场和应力场之间的相互作用和影响被称之为渗流-应力耦合。工程岩体在渗流场与应力场的共同作用下其力学性质与单一场作用下的力学性质有所差别[1-2]。因此,开展岩石在水力耦合作用下的破坏特性研究,对预防隧道围岩坍塌、堤坝塌陷等具有实际意义。
国内外学者在岩石渗流-应力耦合作用下岩石的各项性质展开了不少研究,得到了很多成果。曾晋[3]分析了黏土岩在不同地质环境下的变形特征、渗透特性、损伤及声发射演化特征。孙文吉斌[4]得到页岩中局部化带的出现对渗透率有抑制作用。张超等[5]从力学角度解释了岩体渐进性破坏过程,并揭示了渗流-应力耦合试验中岩体的致灾演变规律。刘晓冬[6]对煤样和页岩试件进行了不同应力条件下的实验,分析了不同应力条件下煤样和页岩试件的力学特性、渗流特性及孔裂隙演化规律。KOU等[7]揭示了岩石三维碎片的分形维数与其最大渗透性之间存在正相关。HAMIEL 等[8]分析了在剪切作用条件下岩石的非线性特征、膨胀特性及孔隙水压力的变化。XIAO 等[9]通过渗流-应力耦合试验分析了岩石的变形破坏及渗流特性,进而探究了岩石在渗流-应力耦合作用下的破坏机制。张培森等[10-13]推导出岩石损伤指标与渗透率的关系式,揭示了渗透率随岩石损伤指标变化的演化规律。
在研究岩石变形局部化时,采取CT 扫描、数字图像相关技术等技术手段对变形局部化的形成进行观测及定性、定量分析,并取得了大量的研究成果。TANG 等[14]采用3D-DIC 系统研究了凝灰岩在压-拉循环荷载过程中变形局部化的演化过程,并分析了裂纹扩展对岩石的力学特征参数以及能量耗散的影响。SHARAFIFISAFA[15]、 ALIABADIAN 等[16]采用DIC 技术分别研究了巴西劈裂条件下的3D 打印岩石试样和砂岩圆盘的裂纹萌生和扩展过程。宋义敏等[17]基于数字散斑相关方法和有限元法(DSCM-FEM)进行了相似模型力学参数反演方法研究,使得散斑域内位移测量值和位移仿真值在数值上和规律上都吻合。杨小彬等[18]利用数字散斑相关方法,分析了岩石在等幅循环加载过程中试件变形局部化带位移演化规律。王学滨等[19]采用数字图像相关方法研究了单轴压缩煤样应变局部化过程,并发现最大剪应变和最大主应变的变异系数可以用来较好识别岩石变形局部化的启动。大久保诚介等[20]研发了3DDIC 系统,利用散斑图像技术,尽可能在较大范围内捕捉试验表面的变形并进行分析,且验证了其测量结果的可靠性。
由于岩石试验观测设备的限制,有关砂岩在不同排水条件作用下的表面变形局部化特性研究还较少涉及。鉴于此,笔者基于可视化三轴压缩伺服控制系统和3D-DIC 观测系统,开展了不同排水条件下的砂岩三轴压缩试验,对不同排水条件下砂岩的表面变形场、力学特性、渗流特性、局部化带内外应变差值演化规律及其破裂面微观形貌进行分析。
1 试验方法
1.1 试件制备
试验所需岩样为砂岩(沉积岩),取自重庆市井口镇,质地较为均匀,平均孔隙率为12.32%。经X射线衍射(XRD)获得其矿物主要成分为石英、钠长石、钾长石、白云母和绿泥石。按照国际岩石力学学会(ISRM)标准[21]对岩块进行取芯、切割、研磨,将试件制备成ø25 mm×50 mm 的圆柱形试件,端面平整度控制在0.02 mm 之内。对加工好的试件进行波速测定,平均P 波波速为3 172 m/s,筛选波速相近的试件用于试验。对筛选后的试件在其侧面涂上防水胶以及制作适用于3D-DIC 系统的散斑,如图1 所示。表1 为砂岩在单轴压缩下的物理力学参数。

表1 单轴压缩下砂岩的物理力学参数Table 1 Physical and mechanical parameters of sandstone under uniaxial compression

图1 制备完成的砂岩试件Fig.1 Processed sandstone specimen
1.2 试验设备
试验所用设备为可视化三轴压缩伺服控制试验系统[22],如图2 所示。其中加载系统主要由轴向加载机架、轴压油源系统、围压加载系统、水压加载系统组成,系统的最大轴向荷载为500 kN,最大轴向位移为10 mm。3D-DIC 系统包含图像采集系统、标定系统、采集控制及分析系统,其中采集系统的6 台工业相机两两组合均匀分布于透明三轴围压室周围。水压加载系统采用ISCO 公司生产的260D 型柱塞泵,其流量范围为0.001~107 mL/min,压力范围为0.07~51.7 MPa,外接数据采集卡,采用DAM3000型高级测控系统来对渗流数据进行实时监测。图3a、图3b 分别为在排水条件下和不排水条件下三轴围压室出口处的状态,排水条件下将出口处打开,允许流体通过,不排水时对其进行密封处理。

图2 可视化三轴压缩伺服控制试验系统Fig.2 Visualize the three-axis compression servo control test system

图3 不同排水条件示意Fig.3 Schematic diagram of different drainage conditions
1.3 试验方案及试验步骤
本次试验设置围压恒定为6.0 MPa,在排水条件和不排水条件下,进水口水压均分别设定为0、2.0 、3.5、5.0 MPa,出水口则按照是否排水设定打开或封闭,试验方案见表2。
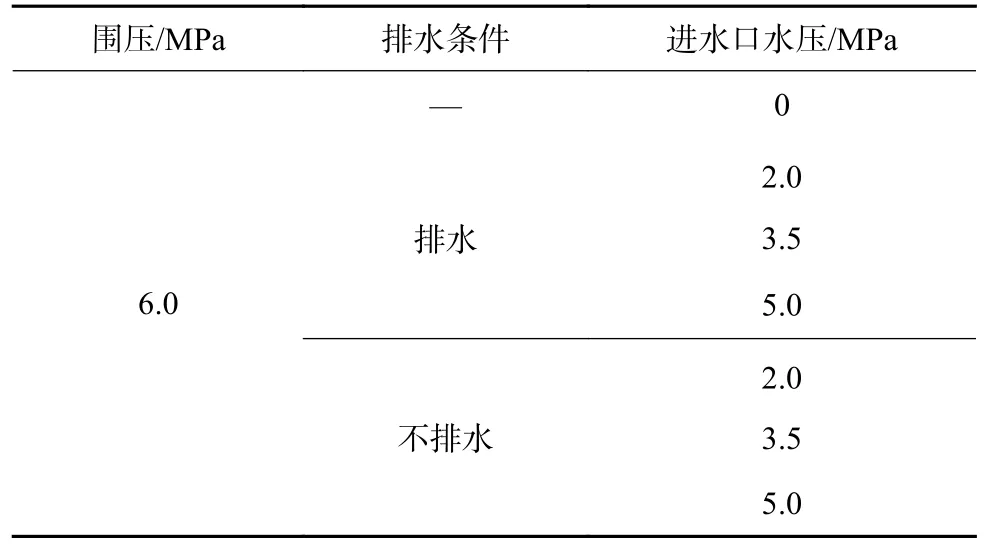
表2 试验方案Table 2 Experimental conditions
具体试验步骤如下:
1)对砂岩试件进行3D-DIC 系统使用前的预处理,在试件侧面涂抹防水胶,并制作人工散斑(白底黑斑),使喷漆与试件表面充分贴合后,将带有散斑的试件放置于真空饱水器中,饱水48 h 至试件完全饱水后开展试验。
2)将饱水状态的试件放置于三轴围压室的上下端块之间,并套上透明热缩管后使用热风枪均匀吹紧,确保热缩管与岩样表面保持紧密接触,再用防水胶对两端的缝隙处进行密封,待防水胶充分凝固后进行围压室的组装,若进行排水状态下的试验,则将出水口打开,使其连接大气压,若进行不排水条件下的试验,则使用生料带和螺帽封住出水口。
3)打开加载系统和3D-DIC 系统的控制硬件和软件,先施加6.0 MPa 的轴压和6.0 MPa 围压,再施加试验方案所设定的水压,并保持3 h 使试件内部的水压分布达到动态平衡,再开始三轴压缩试验。
4)对破坏后的砂岩试件破裂面拍照并取样进行电镜扫描(SEM),以分析渗流-应力耦合作用下不同排水条件对于砂岩断裂面微观形貌的影响。
2 试验结果及分析
2.1 砂岩表面变形场云图演化
根据3D-DIC 系统采集的试件受载破坏全过程的表面图片,分析渗流-应力耦合作用下砂岩表面变形场云图的演化规律。应变场云图中的颜色能够反映应变值的大小及其分布区域,其色度条以拉伸为正值,压缩为负值。根据岩石全应力应变曲线选取6 个具有代表性的时间点,分别为加载起始点(A点),弹性阶段的起始点(B点),屈服点(C点),应力峰值点(D点),出现贯通裂纹的点(E点),残余强度点(F点)。图4 为岩石在排水条件下围压6.0 MPa、渗透水压2.0 MPa 时的应力-应变曲线,展示了6 个特征点在应力-应变曲线上的位置,其他条件下的特征点选点与该条件一致。
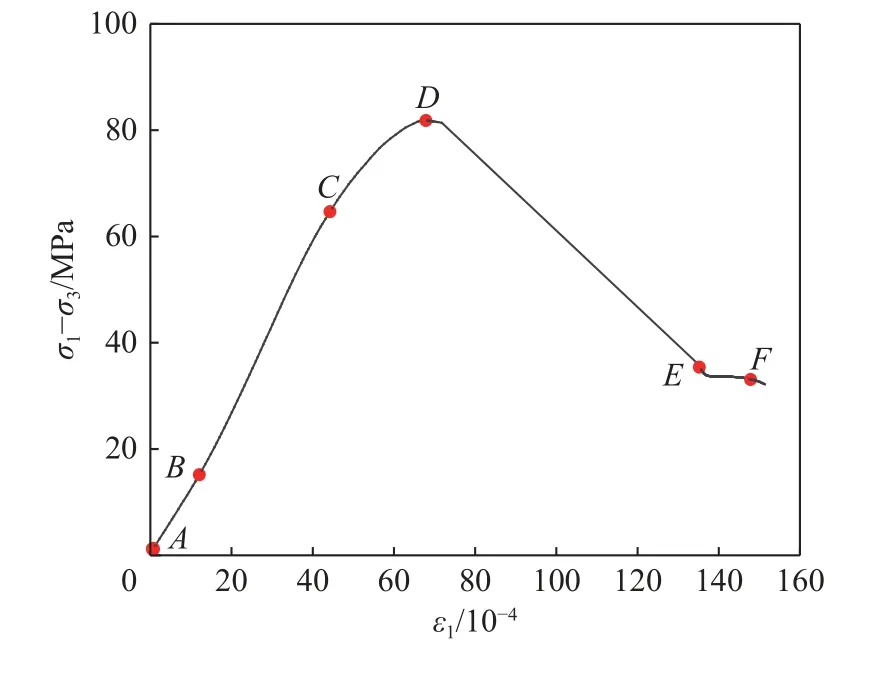
图4 变形场云图演化特征点选取Fig.4 Selection of evolution feature points of deformation field cloud map
在排水条件下,以渗透水压为2.0 MPa 下砂岩三轴压缩过程中的6 个特征点径向应变云图为例进行砂岩变形局部化演化分析,如图5 所示。砂岩在渗流-应力耦合作用下6 个特征时刻点径向应变场云图较好地展示了岩样3 个面(L1、L2、L3)的变形局部化渐进破坏特征。A点为加载起始点,云图呈现出均匀的绿色,此时还没有产生变形;B点为砂岩弹性阶段的起始点,云图分布较为均匀,忽略噪点的影响,面上出现了一些零散的点,表明岩石表面已经开始出现径向变形;C点为岩石的屈服点,较B点而言出现了部分径向应变增大的现象,黄色的点增多;D点为应力峰值点,此处变形逐渐增大,黄色区域逐渐扩大,但尚未形成变形局部化带;E点处岩石出现宏观裂纹, L1 面呈现一条完整变形局部化带,L2 和L3面拼凑起来形成一条与L1 面对称的变形局部化带,说明变形局部化带出现在峰后阶段;F点为岩石的残余变形强度点,受围压的限制作用,其变形局部化带较E点略有增大,但变化不太明显。图6 为在排水条件下,渗透水压2.0 MPa 下砂岩三轴压缩过程中的轴向应变场云图。在峰值强度之前,试件的轴向应变变化比径向应变明显,试件呈整体被压缩的趋势。轴向应变场在E点后的演化规律与径向应变场相似,其变形局部化带内区域呈蓝色。
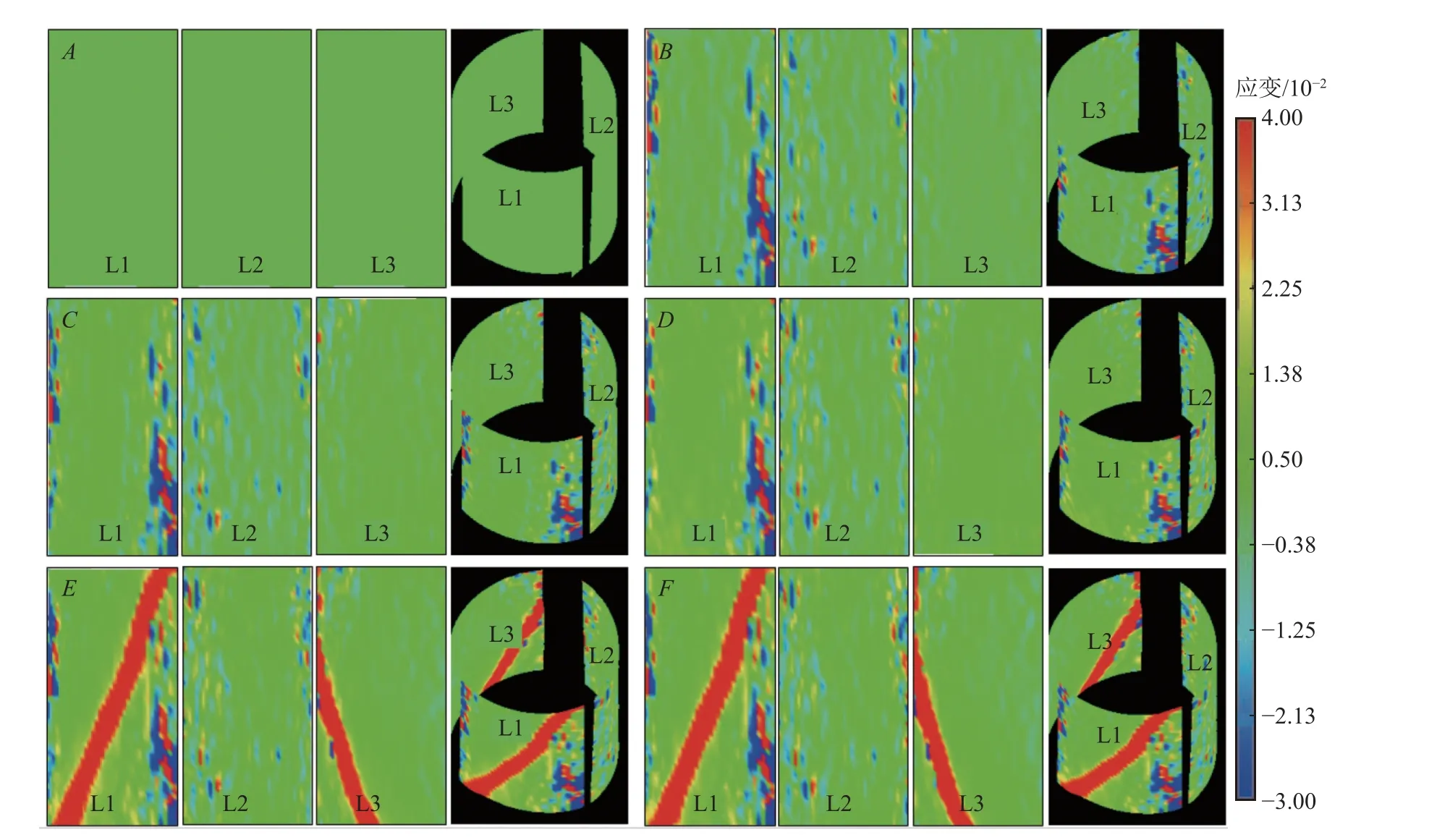
图5 排水条件下不同时刻的径向应变场云图(水压为2.0 MPa)Fig.5 Cloud diagram of radial strain field at different times under drainage conditions (the seepage pressure is 2.0 MPa)
图7 为不同排水条件下砂岩在F点时刻的径向应变场云图,图8 为不同排水条件下砂岩在F点时刻的轴向应变场云图,不同排水条件下的云图均采用相同的色度条,由岩石破坏形态可知岩石在6 种排水条件下均发生剪切破坏,破坏产生的断裂面为单一斜剪切结构面。逐一对比相同渗透水压时在排水条件和不排水条件下的云图,试件在不排水状态下其流体质量处于一种极限状态,径向变形的趋势越明显,形成的变形局部化带更宽,即大应变的区域面积更大。这是由于在不排水的条件下,其渗流通道处于封闭状态,水流不能将岩石内部的矿物颗粒带走,其不溶或难溶性矿物颗粒移动到岩石裂纹发展处并产生作用力,促使岩石裂隙的生成与扩展[23]。由于岩石内部流体质量不变以及孔隙的随机分布,岩石内部裂纹起裂处所承受的力不均匀,导致裂纹扩展的范围更大,表现出2 条变形局部化带不完全对称的现象。而在排水条件下,岩石内部的渗透水压具有连贯性,在轴压、围压以及孔隙水压的综合作用下,岩石发生剪切破坏的特征更明显,裂纹断裂区域更加集中,其变形局部化带展现出对称的趋势[24]。
2.2 排水条件对砂岩力学特性的影响
通过3D-DIC 技术,在变形场云图上布置虚拟应变片来获得应力与应变数据,图9 为不同排水条件下的应力-应变曲线及力学参数演化规律曲线。
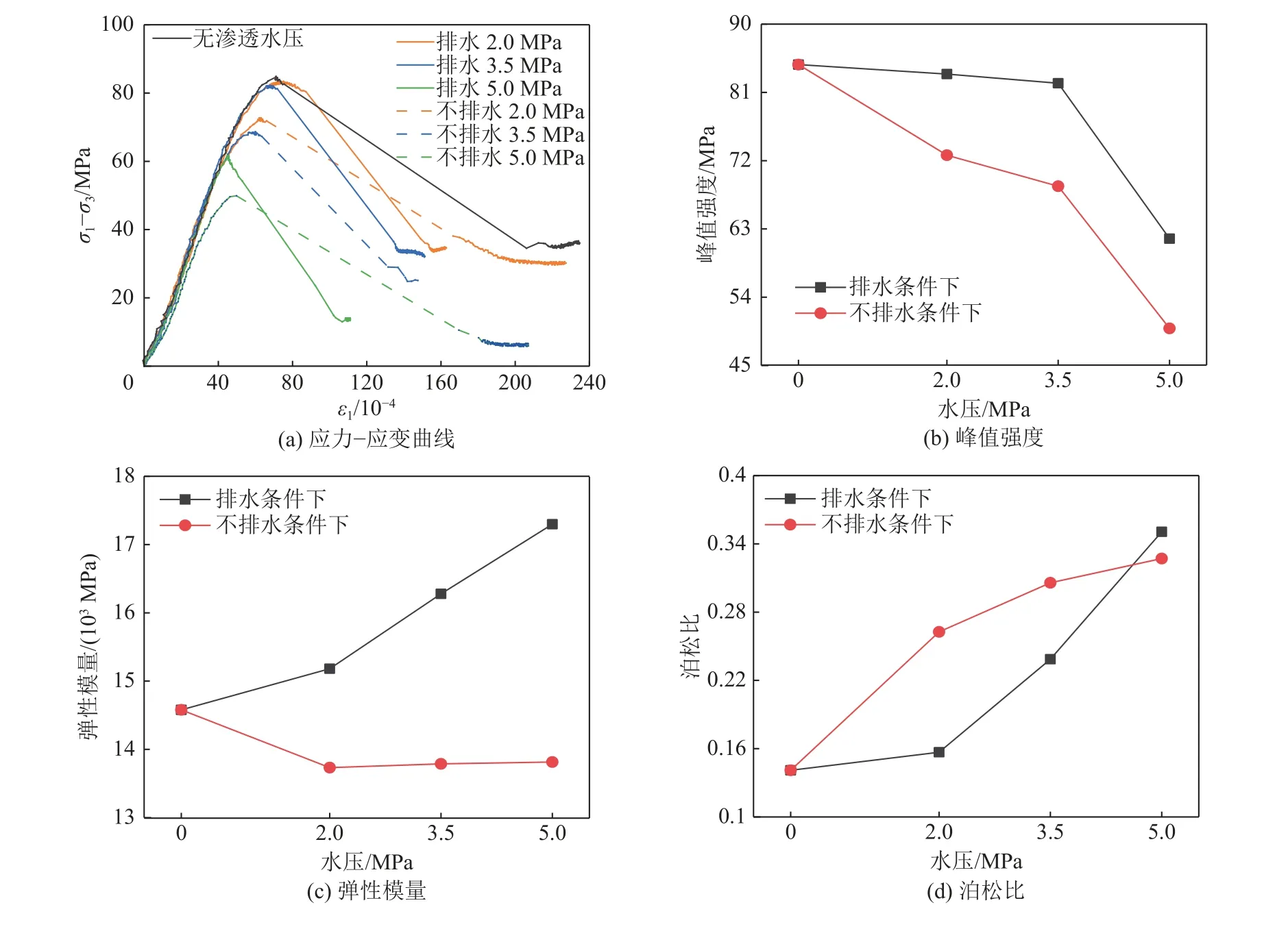
图9 不同排水条件下的应力-应变曲线及力学参数演化曲线Fig.9 Stress-strain curves and evolution curves of mechanical parameters under different drainage conditions
从图9a 可以看出,在相同的加载速率下,岩石在不排水条件下峰值强度出现的时间早于排水条件下峰值强度出现的时间,即岩石在不排水条件下更容易被破坏。从图9b—图9d 可以看出,岩石的峰值强度随渗透水压的增大而减小,弹性模量、泊松比随渗透水压的增大而增大,岩石在常规三轴压缩下的峰值强度高于有渗透水压作用时的值,排水条件下的弹性模量高于常规三轴压缩下的值,不排水条件下的弹性模量低于常规三轴压缩下的值,常规三轴压缩下的泊松比低于有渗透水压作用时的值。对比不同排水条件下的各力学参数发现,不排水条件下的峰值强度低于排水条件下的值,其均值约低了12 MPa,在渗透水压2.0、3.5、5.0 MPa 下,不排水比排水条件下峰值强度分别减少了14.9%,18.13%和20.23%,且随着渗透水压的增大其弱化现象越明显,这是由于岩石在不排水时受到更明显的应力集中,更容易发生破坏所致,说明岩石在受到水压作用但流体不能流出岩石内部时,发生失稳破坏的风险更大。岩石在不同排水条件下峰值强度被弱化的现象与王伟等[25]的研究结果一致。排水条件下的弹性模量大于不排水时的值,且随着渗透水压的增大其在排水条件下的增值明显,不排水条件下的增值不明显,致其差值越来越大,相应地岩石在排水条件下更不容易变形,故其在排水条件下产生的变形局部化现象相对较弱,这与前文其变形局部化带所呈现的结果相对应。泊松比在低渗透水压时不排水条件下的值高于排水条件下的值,但随着渗透水压的增大,排水条件下的增幅更明显,当渗透水压为5.0 MPa 时,不排水条件下的泊松比高于排水条件下的泊松比。在渗透水压的作用下,岩石的峰值强度被弱化,即所能承受的轴压减小,渗透水压越大,岩石内部孔隙水流量越多,其径向变形的趋势越大,故其泊松比也随之增大。
2.3 排水条件对砂岩的渗透特性的影响
当砂岩处于不排水条件时,出水口处于封闭状态,故不讨论不排水条件下砂岩的渗透特性,仅讨论排水条件下砂岩的渗流特性。本文选用稳态法测试砂岩的渗透率,根据水压加载系统所采集到的渗流量,利用达西定律计算出试验时间内的渗流率,公式为
式中:k为砂岩在 Δt时间内的平均渗透率,m2;μ为水的动力黏滞系数,取μ= 100.5×10-5Pa·s(温度T=20 ℃); ΔQ为 Δt时间内渗过砂岩试件的水流体积,m3;L为砂岩高度,m;A为试件横截面面积,m2;ΔP为岩样渗流上、下游渗透压差,ΔP=P1-P2,P1 和P2分别为渗流上、下游压力,Pa;Δt为记录点间隔时间,s。
图10 为排水条件下砂岩渗透率随时间的变化曲线,由图10 可知,在加载初期,渗透率出现略微的下降,这是因为岩石处于压密阶段,岩石的内部孔隙作为流体的渗流通道在应力的作用下而闭合,由于在试验开始前已经对试件施加了3 h 的围压和水压,导致其被压缩闭合的阶段表现得并不明显。而随着岩石应力的加载,岩石内部开始出现微裂纹,微裂纹之间相互连接形成裂隙,且矿物颗粒被水流带走形成孔洞,从而形成新的渗流通道,渗透率也随之增大。当砂岩出现宏观裂纹时,砂岩内部存在稳定的渗流通道,渗流量出现迅速增长的现象。试样发生破坏后,停止试验的第一步即为停止水压,此时砂岩受到轴压、围压的作用,渗透率迅速下降。对比不同渗透水压下的渗透率变化曲线可以发现,随着渗透水压的增大,砂岩渗透率的最大值出现的时间点就越早,这是因为随着渗透水压的增大,在试验加载过程中岩石受到的轴压不断增大,试样内部产生微裂纹后,水不断流动和填充,水压越大使得其微裂纹扩展更迅速,相应更早进入损伤屈服阶段,砂岩出现贯通裂纹的时间更早,这与砂岩的应力应变曲线呈现的规律一致。岩石在同一围压不同渗透水压下其渗透率的变化规律与其他学者[26]的研究结果具有一致性。

图10 排水条件下渗透率随时间演化曲线Fig.10 Evolution curve of permeability with time under drainage conditions
2.4 排水条件对变形局部化启动应力的影响
通过3D-DIC 技术,可以在观测面的任意位置布置虚拟应变片,为获得砂岩由均匀变形向非均匀变形转化的应力水平,在主应变场云图的变形局部化带内外布置了虚拟应变片,其布置方式如图11 所示。
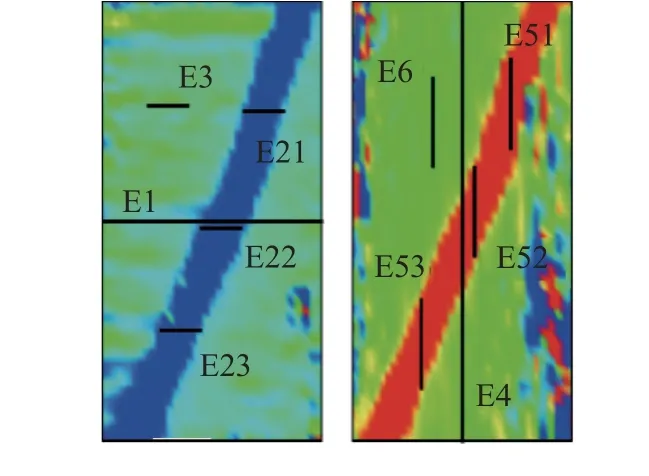
图11 虚拟应变片布置示意Fig.11 Schematic diagram of the arrangement of virtual strain gauges
在径向应变云图中,在试件中部由左至右布置一条虚拟应变片作为E1,在变形局部化带内由上至下布置等长的3 条虚拟应变片E21、E22、E23,取其均值E2 作为变形局部化带内的应变值,在变形局部化带外布置一条与E2 等长的虚拟应变片E3,作为变形局部化带外的应变值。在轴向应变云图中,在试件中部由上至下布置一条虚拟应变片作为E4,在变形局部化带内由上至下布置等长的3 条虚拟应变片E51、E52、E53,取其均值E5 作为变形局部化带内的应变值,在变形局部化带外布置一条与E5 等长的虚拟应变片E6,作为变形局部化带外的应变值。
图12,13 和14 分别为不同位置处的虚拟应变片在渗透水压2.0、3.5、5.0 MPa 条件下砂岩的变形局部化带内外应力差-应变曲线。其中图12a、图13a、图14a 为应力差-径向应变曲线,图12b、图13b、图14b为应力差-轴向应变曲线。由图12—图14 可知,在峰值强度前,不同排水条件下的径向应变E1、E2、E3 曲线的应变值均随应力的增大近似呈线性增加,表明岩石处于弹性阶段,表面还未出现明显的宏观裂纹,这与应变场云图观测到的结果一致。在峰值强度之后,E1、E2 的应变值均增大,但位于变形局部化带内的E2 的增值远大于整体E1 的增值,而位于变形局部化带外的E3 的值则略有缩小,即出现弹性卸载现象。这种现象表明在峰后阶段变形局部化带内外的应变值相差很大,且带内的应变远大于带外的应变。局部化带外区域发生的应变属于弹性应变,在应力加载阶段,其吸收的能量以弹性应变能储存起来,到达应力阈值时,带外区域将自身的能量以弹性能的方式释放到带内区域促进宏观裂纹的发展,岩石发生剪切破坏。从峰后阶段E1、E2、E3 的差值可知,岩石的整体径向应变反映的是变形局部化带和带外未破坏区域的综合应变关系,而不能体现岩石变形局部化带内外区域应变的差异性。对比各条件下应力差-轴向应变曲线,发现其变化规律和径向应变的演化具有一致性。
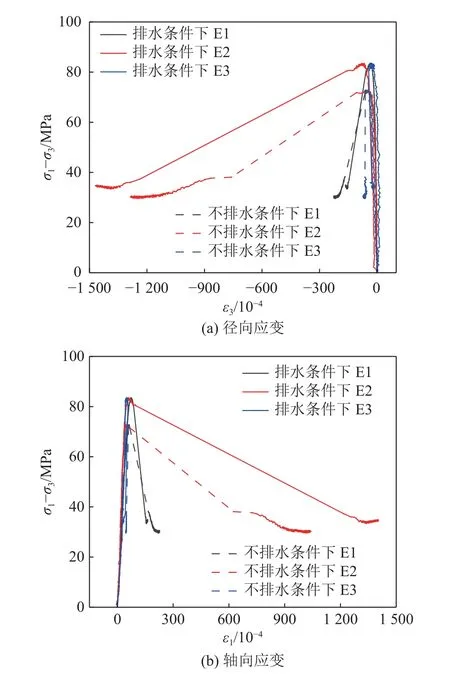
图12 渗透水压2.0 MPa 下砂岩变形局部化带内外主应力差-应变曲线Fig.12 Main stress difference-strain curve of sandstone deformation localization zone under seepage pressure of 2.0 MPa

图13 渗透水压3.5 MPa 下砂岩变形局部化带内外主应力差-应变曲线Fig.13 Main stress difference-strain curve of sandstone deformation localization zone under seepage pressure of 3.5 MPa
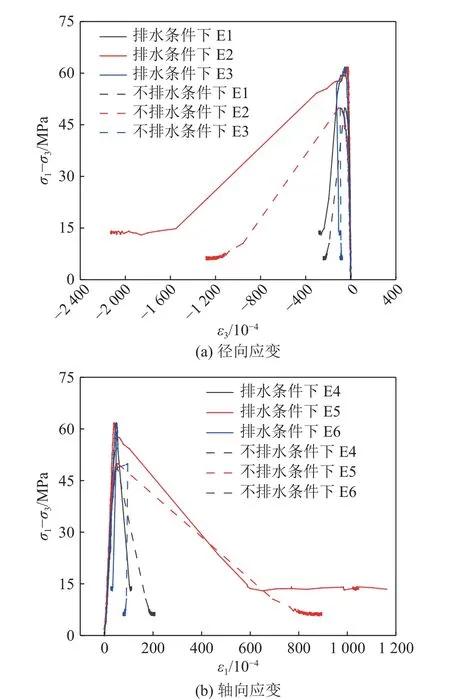
图14 渗透水压5.0 MPa 下砂岩变形局部化带内外主应力差-应变曲线Fig.14 Main stress difference-strain curve of sandstone deformation localization zone under seepage pressure of 5.0 MPa
根据砂岩变形局部化带内外的三条不同位置处的径向、轴向应变曲线,绘制应变差值曲线,图15 为在排水条件下,渗透水压为2.0 MPa 时的变形局部化带内外的应变差值演化曲线,将在相同排水条件下的径向、轴向应变差值曲线绘制在同一图中,可以确定该条件下的径向、轴向变形局部化启动应力。在加载初期,各差值基本为0,随着加载的进行,曲线会出现分叉现象,此时岩石内部结构发生变化,微裂纹开始萌生、扩展,将该分叉点所对应的应力称为变形局部化启动应力[27]。
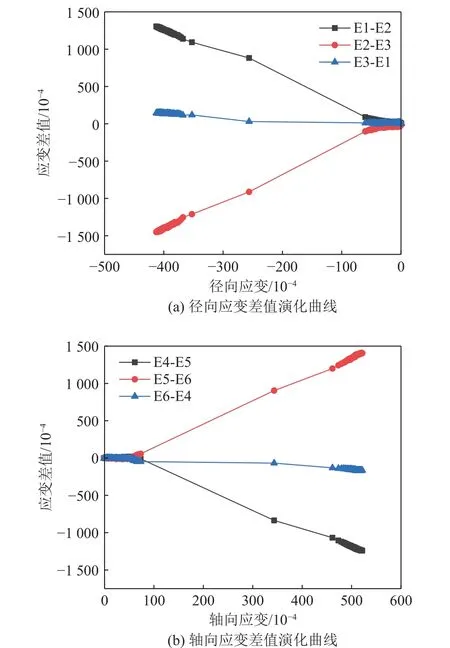
图15 变形局部化带内外应变差值演化曲线Fig.15 Evolution curve of the difference between internal and external strains in the deformation localization zone
根据分叉点所确定的变形局部化启动点的应力值及应力水平见表3。由表3 可知,渗透水压相同时,岩石在排水条件下的径向启动应力水平、轴向启动应力水平均高于不排水条件下的值,径向启动应力水平的均值从98.08%变化为96.23%,其均值低了1.85%,轴向启动应力水平的均值从97.02%变化为94.81%,其均值低了2.21%。随着渗透水压从2.0 MPa 增加到5.0 MPa,岩石在排水条件下的径向、轴向启动应力水平的增值分别为1.52%、1.32%,在不排水条件下的径向、轴向启动应力水平的增值分别为2.52%、1.88%,说明不论岩石排水或不排水,其变形局部化径向、轴向启动应力水平均随渗透水压的增大而增大,即启动的时间点更提前,岩石在不排水的条件下启动应力水平受渗透水压的影响更明显。将其在排水条件下的变化规律与彭守建等[26]的研究结果对比可知,在同一围压下,岩石的启动应力水平随着渗透水压的增大而增大,结合其研究结果可知,当渗透水压相同时,其启动应力水平随着围压的增大而减小。对比不同条件下岩石的径向、轴向变形局部化启动点可知,无论在何排水条件下径向变形局部化启动点始终高于轴向变形局部化启动点。
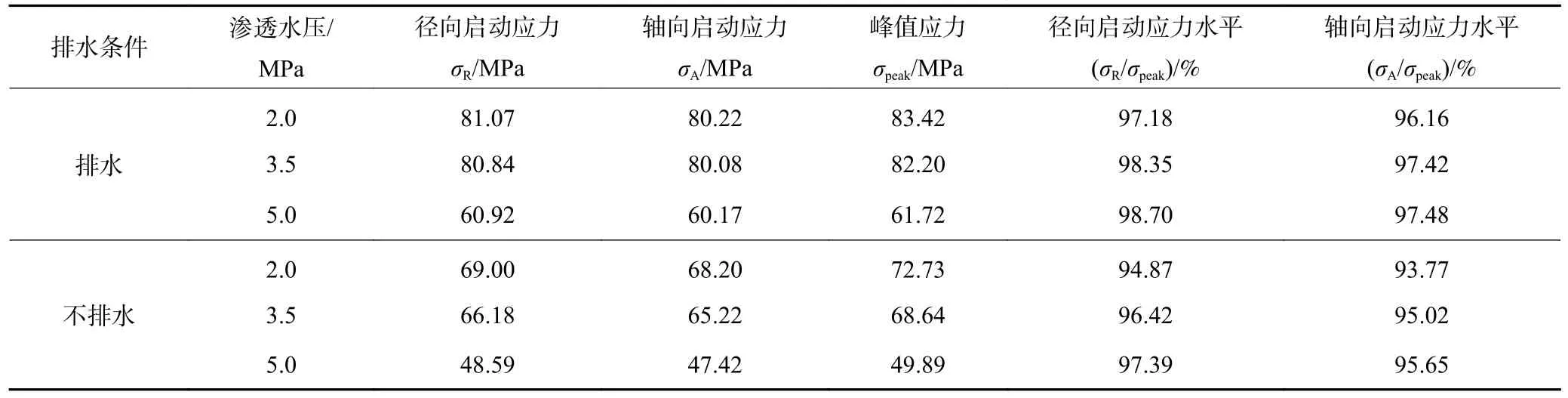
表3 不同排水条件下变形局部化启动点相关参数统计Table 3 Statistics on the parameters related to the start point of deformation localization under different drainage conditions
为定量分析不同排水条件对变形局部化启动应力的影响,对表3 中的数据进行了回归拟合,结果见表4。据拟合结果可知,岩石在排水条件下的启动应力水平与渗透水压呈指数型回归,岩石在不排水条件下的启动应力水平与渗透水压呈较好的线性关系,岩石处于排水及不排水条件时,其径向的拟合结果优于轴向的拟合结果,岩石在不排水条件下的启动应力及应力水平受渗透水压的影响比排水时更敏感。

表4 应力水平和排水条件之间的拟合结果Table 4 Fitting result between stress levels and drainage conditions
2.5 岩石破裂面及微观特征分析
图16 为各排水条件下发生破坏后的试样,试验结束后,去除热缩管时,部分散斑被热缩管带走,故其表面散斑呈不完整状态,通过观察可知,其宏观裂纹呈单一剪切破坏,和表面变形场云图所呈现的变形局部化带一致。图17 为水压为2.0 MPa 时的岩石破裂面,在不排水的条件下岩石发生宏观破坏前其渗流通道不具有连续性,可见在不排水条件下岩石的颗粒感更强,破裂面表面更粗糙,后续将结合电镜扫描进一步分析其结构上的差异。

图16 不同排水条件下破坏后的试件Fig.16 Damaged specimens under different drainage conditions

图17 不同排水条件下的岩石破裂面(水压2.0 MPa)Fig.17 Rock fracture surface under different drainage conditions (water pressure 2.0 MPa)
选取不同排水条件下的岩石试件,对破裂面进行电镜扫描,放大倍数为500 倍,如图18 所示。以渗透水压2.0 MPa 为例,在岩石断裂面上选择2 个不同的位置进行观察。

图18 不同排水条件下的SEM 扫描Fig.18 SEM scan under different drainage conditions
从图18 可以看出,岩石在排水条件下,水流将岩石内部的矿物颗粒带走,胶结结构被破坏,孔隙发育,颗粒间的裂纹联通,破裂面光滑,矿物结构表面颗粒松散,其形成的孔洞较大,而在不排水条件下,水流将岩石内部的不溶或难溶性物质带到岩石裂纹发展处,颗粒表面有片状岩屑附着,胶结基质中发育微裂纹,基质溶蚀形成孔洞,但相对于排水条件下的孔洞较小。岩石内部由于存在孔洞、微裂隙等,就会产生应力集中而发生破裂,结合岩石表面变形场云图及电镜扫描的结果可知,岩石在不排水条件下的应力集中现象比在排水条件下更明显。
3 结 论
1)随着渗透水压的增大,砂岩的峰值强度减小,弹性模量、泊松比增大,排水条件下其渗透率最大值出现的时间越早。由于岩石在不排水时受到更明显的应力集中更易发生破坏,渗透水压相同时,不排水条件下的峰值强度比排水条件下均值低12 MPa。排水条件下的弹性模量大于不排水时的值,且随着渗透水压的增大其差值愈发明显。
2)当水压相同时,砂岩在不排水条件下的变形局部化带比在排水条件下的变形局部化带更宽,即宏观裂纹更明显。岩石在排水条件下破裂面光滑,由于水流带走了岩石内部的矿物颗粒,其孔洞更大,而在不排水条件下,岩石破裂面有岩屑附着,由于水的物理润滑、化学弱化等作用,促使微裂纹更快发育扩展,使得岩石更早产生宏观裂纹。
3)无论在何排水条件下径向变形局部化启动点始终优先于轴向变形局部化启动点。岩石在排水条件下的径向启动应力水平、轴向启动应力水平均高于不排水条件下的值,平均分别提高了1.85%和2.21%。水压相同时,岩石在不排水条件下的启动应力及应力水平受渗透水压的影响更显著。

