基于模糊粗糙集的无监督动态特征选择算法

马磊，罗川*，李天瑞，陈红梅

基于模糊粗糙集的无监督动态特征选择算法

马磊1，罗川1*，李天瑞2，陈红梅2

（1.四川大学 计算机学院，成都 610065； 2.西南交通大学 计算机与人工智能学院，成都 611756）（ ∗ 通信作者电子邮箱cluo@scu.edu.cn）

动态特征选择算法能够大幅提升处理动态数据的效率，然而目前基于模糊粗糙集的无监督的动态特征选择算法较少。针对上述问题，提出一种特征分批次到达情况下的基于模糊粗糙集的无监督动态特征选择（UDFRFS）算法。首先，通过定义伪三角范数和新的相似关系在已有数据的基础上进行模糊关系值的更新过程，从而减少不必要的运算过程；其次，通过利用已有的特征选择结果，在新的特征到达后，使用依赖度判断原始特征部分是否需要重新计算，以减少冗余的特征选择过程，从而进一步提高特征选择的速度。实验结果表明，UDFRFS相较于静态的基于依赖度的无监督模糊粗糙集特征选择算法，在时间效率方面能够提升90个百分点以上，同时保持较好的分类精度和聚类表现。

特征选择；模糊粗糙集；动态数据；无监督特征选择；依赖度

0 引言

特征选择是模式识别中一种非常重要的预处理手段，通过去除不相关和冗余的特征，达到精简样本集合、提高后续识别过程的效率并提升精度的目的。粗糙集作为一种重要的特征选择模型，由Pawlak［1］提出，主要用于处理不完整、不精确的数据；但是粗糙集只能处理分类型变量，无法处理实际生活中广泛存在的连续型变量。Dubois等［2］将粗糙集理论和模糊集理论［3］结合，提出了模糊粗糙集理论。在该理论中，通过将等价关系替换为模糊相似关系，弥补了粗糙集只能处理分类型变量的缺点。此后，大量基于模糊粗糙集理论的特征选择算法被提出。An等［4］结合了相对测量和模糊粗糙集，提出一种新的特征选择方法，以解决数据集的类密度差异较大时模糊粗糙集理论无法有效评估样本的分类不确定性的问题。Chen等［5］提出一种基于超图的模糊粗糙集特征选择算法，从而提升该算法在大规模数据集下的时间性能，并在精简特征集合的基础上获得了较好的分类精度。Yang等［6］提出一种噪声感知模糊粗糙集算法，相较于传统的基于模糊粗糙集的特征选择算法，该算法的抗噪声特性更好。

大数据时代的数据规模越来越庞大，各领域每时每刻都在产生新的数据。针对数据体量庞大的问题，一系列基于粗糙集及其扩展模型模糊粗糙集的方法被提出。章夏杰等［7］提出一种Spark平台下的分布式粗糙集属性约简算法，通过引入改进鲸鱼优化算法实现特征选择功能，并将该算法并行化，使它在大数据环境下可以充分利用集群优势，提高算法的运行速度。危前进等［8］提出一种基于粗糙集的多目标并行属性约简算法，该算法将粗糙集理论和蚁群优化算法相结合，通过MapReduce平台并行化，从而实现更好的时间效率，以应对大规模数据。但是这些数据不断更新换代，通常是分批到达的，呈现动态性。如果使用静态算法，将旧数据和新数据一起重新处理，就无法有效利用之前的特征选择结果，导致产生较大的时间代价。为了解决该问题，研究者提出一系列动态特征选择算法。Yang等［9］提出一种基于关系矩阵的动态模糊粗糙集特征选择算法，并分开讨论单个新样本和多个新样本到达的情况；相较于静态算法，该算法的时间效率更高。Wan等［10］从特征相关关系出发，提出一种基于模糊依赖度的动态模糊粗糙集特征选择算法。该算法考虑了交互关系、条件特征与决策类的关系和特征权重随特征子集变化的动态变化。Ni等［11］在模糊粗糙集的基础上通过引入包含代表性样本的关键实例集，在新的样本到达时选择并补充新的特征；由于关键实例集远小于整个数据集，该特征选择算法能有效减少冗余计算。程玉胜等［12］提出一种基于粗糙集的数据流多标记分布特征选择算法，以处理流特征数据的特征选择问题。通过特征和标记之间的相关性、特征和特征之间的相关性这两个标准形成候选特征集合，使得该算法在特征动态更新的背景下能够保持较好的性能。曾艺祥等［13］提出一种基于层次类别邻域粗糙集的在线流特征选择算法，该算法使用经过改进的粗糙集模型（邻域粗糙集），并基于层次依赖度提出了3个在线特征评价函数，使得该算法能处理在线流特征数据。

上述特征选择算法主要在有监督的情况下完成，然而在现实生活中，存在较多不能明确知道样本所属类别的无标签数据。无监督特征选择算法作为一种能够在不需要类标签信息的情况下识别和选择相关特征手段，被应用在许多研究领域［14］。在基于粗糙集及其扩展模型模糊粗糙集的无监督特征选择领域，Velayutham等［15］基于粗糙集模型提出一种基于依赖度的无监督特征选择算法。此后，Velayutham等［16］又提出一种基于信息熵的粗糙集无监督特征选择算法。与有监督特征选择算法相比，这些特征选择算法将重点从条件属性和决策属性之间的关系，转移至条件属性之间的关系上。在模糊粗糙集领域，Mac Parthaláin等［17］基于依赖度、边界区域、关系矩阵和替代模糊分辨方法，提出基于模糊粗糙集的无监督特征选择（Unsupervised Fuzzy-Rough Feature Selection， UFRFS）算法；Yuan等［18］使用模糊粗糙集处理无监督混合数据，以依赖度为基础定义属性的重要度，作为特征选择的基准；Ganivada等［19］将模糊粗糙集和神经网络相结合，提出一种用于识别数据显著特征的粒状神经网络，以达到特征选择的目的。

目前，基于模糊粗糙集的无监督特征选择算法主要是静态特征选择算法，在动态数据集上的研究则较少，而静态特征选择算法存在两方面的问题：1）对于某个备选特征，有监督特征选择算法只需要计算该特征和决策属性的度量性指标，但无监督特征选择算法需要计算该特征和其他所有条件属性的度量性指标，运算量大幅增加；2）在新的数据到达后，依然只能在所有数据的基础上重新计算，无法有效利用之前的结果。本文提出了一种基于模糊粗糙集的无监督动态特征选择（Unsupervised Dynamic Fuzzy-Rough set based Feature Selection， UDFRFS）算法，该算法通过定义伪三角范数和新的相似关系，从而加快度量性指标的计算过程，利用之前的特征选择结果，在新的数据集到达后，减少对原始特征的冗余运算，从而加快特征选择的速度。在9组数据集上的实验结果表明，该算法与静态算法和同类基于依赖度的特征选择算法相比，在新的特征被加入数据集时能够获得更好的时间效率，同时保持较好的分类精度和聚类表现。

1 基础知识

1.1　模糊粗糙集

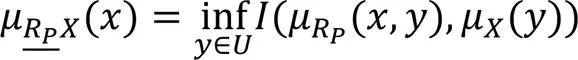
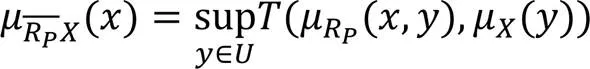
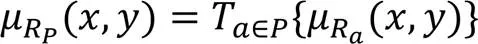
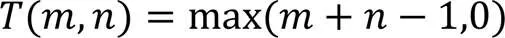
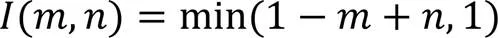
对于模糊相似关系采用以下定义。

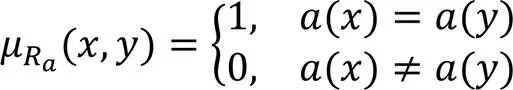
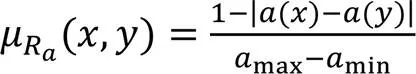
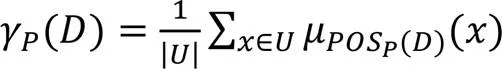
基于依赖度的模糊粗糙集的特征选择过程如算法1所示。

算法1 基于依赖度的模糊粗糙集的特征选择算法。

8） end if

10） end

1.2　基于模糊粗糙集的无监督特征选择

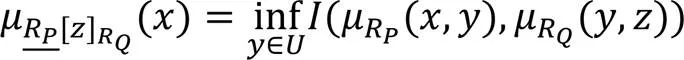
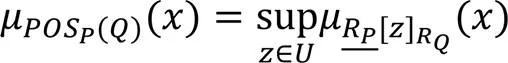
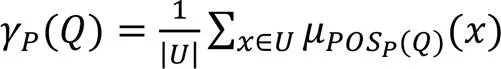
同算法1，对于无监督的情况，依然可以通过定义一个基于依赖度的模糊粗糙集的特征选择算法进行特征选择。

算法2 UFRFS。

7） end if

8） end

2 基于模糊粗糙集的无监督动态特征选择

在大数据时代，数据通常以分批次的形式到达。如果采用如UFRFS算法等静态算法处理这些数据，可能造成较大的时间开销。而动态特征选择算法保留之前数据的计算结果，之后的计算均在这些结果的基础上进行，能够有效降低算法的时间复杂度。

2.1　无监督动态特征选择下的模糊相似度、三角范数和三角余范数

证明 1）由式（3）～（4）可知：

由定理1可知，在增加属性的情况下，新的模糊关系值和旧的模糊关系值之间没有等量关系，不能直接用于加速运算过程。在计算模糊关系值的时候需要使用三角范数，如果能将它扩展，得到一个等量关系，就可以在已有基础上更新模糊关系值，加快运算速度。

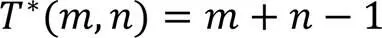
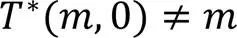
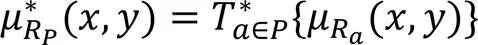
证明 1）由式（14）和式（16）可知：

移项即可得到上述性质。 证毕。

2）由式（14）和式（16）可知：

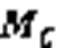
1）当一个特征被加入当前约简集合，只需要运用定理2的性质2）添加该特征。

2）当一个特征被从当前约简集合中去掉，只需要运用定理2的性质1）删除该特征。

2.2　无监督动态特征选择下的向下近似

由2.1节可知，当新的特征到达时，可以利用在原始数据集上计算的模糊关系值，增量地计算新的模糊关系值，从而降低算法的时间复杂度，但是没有有效利用之前计算过程中产生的依赖度信息或特征子集信息。本节将针对此部分进行探讨。

定理4表明当新的特征到达时，向下近似保持不变或者变大。结合式（12）～（13）可以通过推导得出以下结论：

特征选择时，可以先保留原始属性集合计算所产生的依赖度。在新的特征到达后，对于之前已经计算过的部分，根据算法2，仅考虑依赖度小于1的特征。由此可以得出结论：

1）依赖度等于1的原始特征依然不被包含在约简集合中，可以直接跳过，仅更新相似关系矩阵。

2）依赖度小于1的原始特征，现在有可能不在约简集合中，需要计算。如果依赖度依然小于1，则直接跳过，仅更新相似关系矩阵；否则从该特征开始，后续所有的依赖度等于1的原始特征也需要重新计算。

3）新的特征直接重新计算依赖度。

2.3　特征分批次到达情况下基于模糊粗糙集的无监督动态特征选择

由2.1和2.2节，可以得到基于模糊粗糙集的无监督动态特征选择（UDFRFS）算法。

算法3 UDFRFS。

10） else

12） end if

13） end if

14） end

20） end if

21） end

3 实验与结果分析

3.1　实验数据

本文实验将针对UDFRFS算法的运行时间、特征子集大小、分类精度和聚类表现进行分析。实验数据集为9个来自UCI（https：//archive.ics.uci.edu/datasets）和TSC（Time Series Classification）（http：//www.timeseriesclassification.com/）的数据集，如表1所示。本文选取了UDFRFS算法的静态版本UFRFS算法［17］、基于模糊粗糙集的无监督属性约简（Fuzzy Rough-based Unsupervised Attribute Reduction， FRUAR）算法［18］和基于模糊粗糙集的无监督和不完整数据的特征选择（feature Selection for Unsupervised and Incomplete data based on Fuzzy Rough sets， SUIFR）算法［22］作为对比算法。

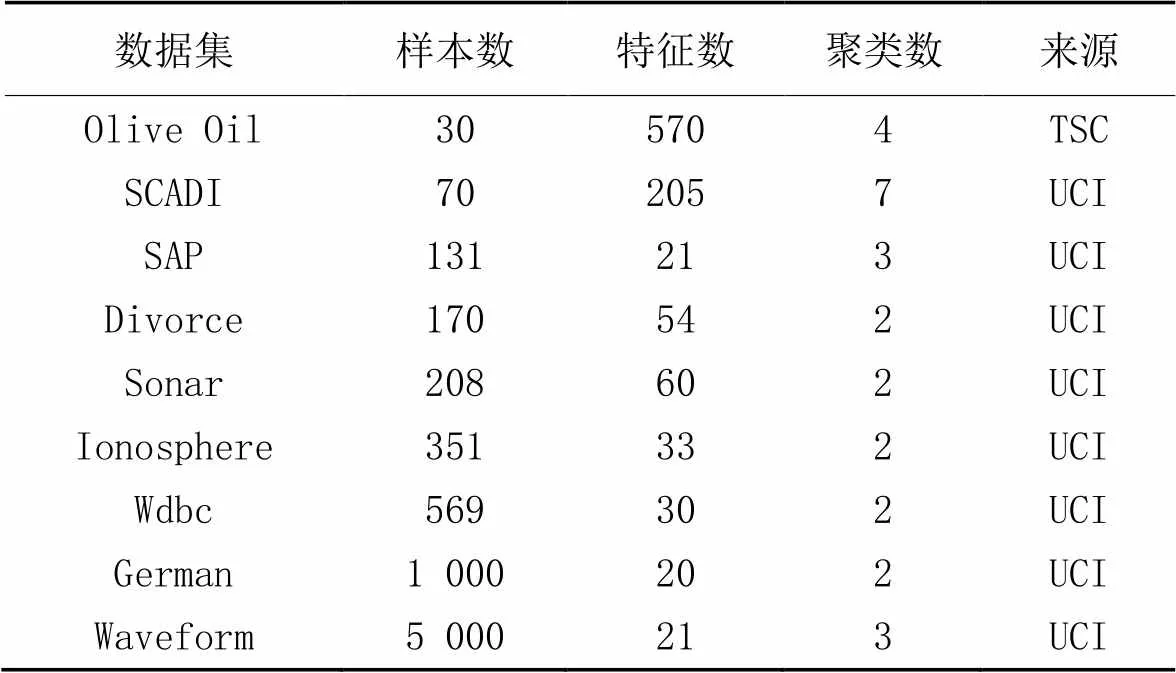
表1　数据集详情

3.2　实验设计

实验在一台配备了Intel Core i7-9700 CPU @ 3.00 GHz中央处理器和32 GB内存的计算机上进行，使用IntelIJ IDEA环境，语言平台是Scala，分类精度和聚类表现的数据使用Weka平台得到。

本文算法在特征动态变化的层面上优化原始算法，因此将根据特征划分各数据集，得到实验中所用的动态数据集。

表1中的每个数据集都将被划分为两个部分：原始的基础数据集和原始的增量数据集。每次实验首先打乱数据集以排除偶然性，其次根据以下两组实验的具体要求，从第0个特征开始，选择符合条件数量的特征及其所对应的列，作为原始的基础数据集；剩下的部分作为原始的增量数据集。

实验将分为两组：

1）不同基础数据集大小对比实验。根据特征划分，将数据集的90%作为原始的基础数据集，剩下的10%作为原始的增量数据集。将原始的基础数据集等量划分成9份，首先选取第1份作为第1次实验使用的基础数据集；其次，基于上一次实验所使用的基础数据集，每次实验都按顺序再选取一份进行组合，从而产生9个大小依次增加的最终使用的基础数据集，分别对应9次实验。每次实验时，从原始的增量数据集中随机选取50%的数据，作为当次实验的增量数据集。

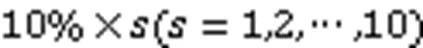
因为UDFRFS算法需要使用基础数据集的约简结果作为输入，所以在每次实验中，首先将基础数据集在静态版本的UFRFS算法上运行一次，保存约简结果，作为后续运算的输入。其次，对于所有算法，将基础数据集和增量数据集结合为一个新的数据集，作为当次实验需要使用到的数据集。

一次完整的实验需要在不同大小的数据集上运行上述的实验组1）9次，实验组2）10次。对于每个数据集，都运行10次完整实验，将每次实验得到的结果取平均值作为实验结果。在分类精度方面，选取了近邻算法（-Nearest Neighbor，NN）（=3）、朴素贝叶斯算法（Naive Bayes， NB）和分类与回归树（Classification And Regression Tree， CART）这3种分类算法作为基准；在聚类表现方面，采用-means聚类算法作为基准。采用10次十折交叉验证（10×10-fold cross-validation）进行实验，将得到结果的平均值作为实验结果。

3.3　实验结果与分析

3.3.1运行时间

表2～3分别为3种算法在不同大小的基础数据集和不同增量数据集上的运行时间对比。其中：“TRR”表示本文算法占对比算法运行时间的百分比；“—”表示该算法的运行时间过长，没有产生实验结果（由19次实验组成的一次完整的实验中，运行前5次实验就已经超过了7 h）。

从表2可以看出，相较于UFRFS，本文算法的TRR指标在每个数据集上均低于10%，表明本文算法在每个数据集的平均执行时间都少于静态版本的10%，即本文算法在运行效率方面均提升了90个百分点以上，即使是在特征数较多的Olive Oil和SCADI数据集，以及样本数较多的Waveform数据集上依然能够保持良好的表现。FRUAR和SUIFR这两个算法更关注特征之间的关系，本文算法在每次循环的时候不考虑之前过程中已经被剔除的特征，但是本文算法也考虑这一部分，因此这两个算法的时间效率比本文算法更低。

3.3.2特征子集大小和分类精度

表4为4种算法运行后所形成的特征子集大小的对比。可以看出，UDFRFS的特征子集大小和UFRFS完全一致。这是因为UDFRFS基于UFRFS改进，均基于一致的特征选择手段，UDFRFS通过利用之前得到的中间结果加速模糊相似关系和依赖度的计算，而这些加速过程并不会影响结果。FRUAR在大部分数据集上和前两种算法的表现相近，在SAP、Divorce、Ionosphere和German上得到的特征子集略大，但是在Olive Oil、SCADI、Sonar和Wdbc上拥有更小的特征子集大小。在上述方面，FRUAR略微优于UDFRFS和UFRFS，特别是在特征数较多的Olive Oil和SCADI上。但是FRUAR的时间消耗较高。对于SUIFR，它采用了高斯核作为计算模糊关系值的标准，在大部分情况下，该算法的特征子集都要远小于除Ionosphere外的其他算法。但是，特征选择并不是特征子集越小越好，过多删除特征也意味着有用信息的缺失会更加严重。

表5～7分别为经过4种算法进行特征选择之后所得到的数据集在NN、NB和CART这3种分类算法下的分类精度对比，其中，“RAW1”表示没有经过特征选择的原始数据集的分类精度。可以看出，UDFRFS的分类精度和UFRFS完全一致，原因在前面已经有所讲述。FRUAR的分类精度和前两种算法相近，在SCADI上取得了更好的效果，但是在Olive Oil和Wdbc上的效果更差。SUIFR和FRUAR在大部分情况下表现相近，但在SCADI、Divorce、Wdbc和German上的表现较差，原因是过小的特征子集虽然能够减少后续实际使用该数据集进行模式识别等任务时耗费的时间，但也会因有用信息缺失过多，导致分类精度降低。需要注意的是，在Olive Oil上，不同算法的表现差异较大，这是因为该数据集只有30个样本，但是却有570个特征，并且从特征选择的结果可以得知，该数据集包含有大量的冗余特征，这显然影响了分类结果。

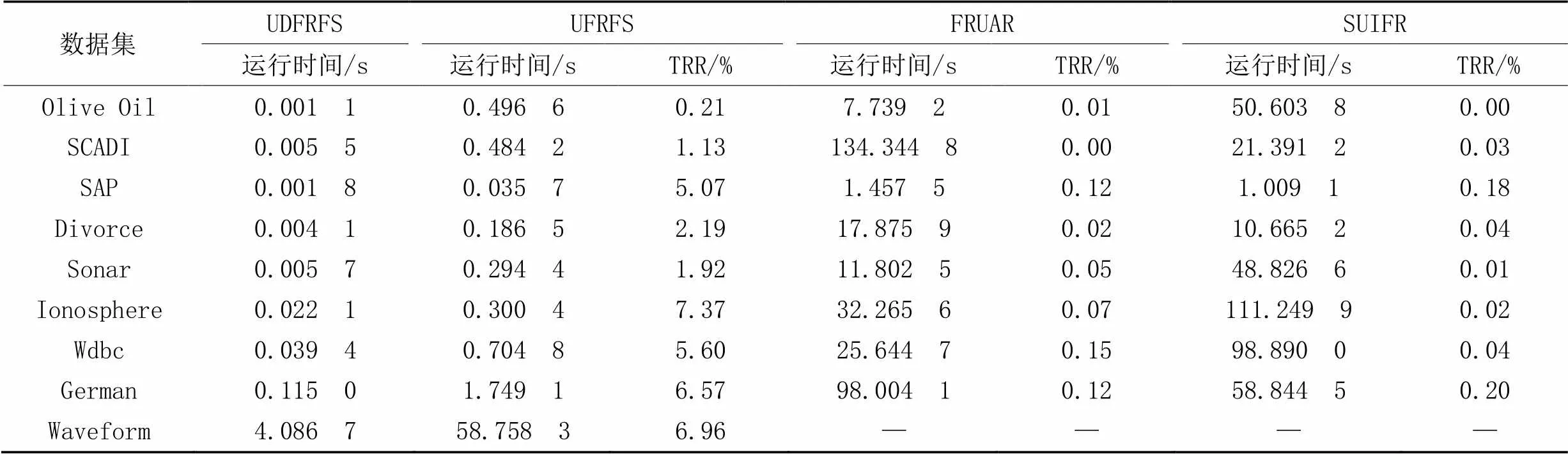
表2　不同大小基础数据集上不同算法的运行时间对比

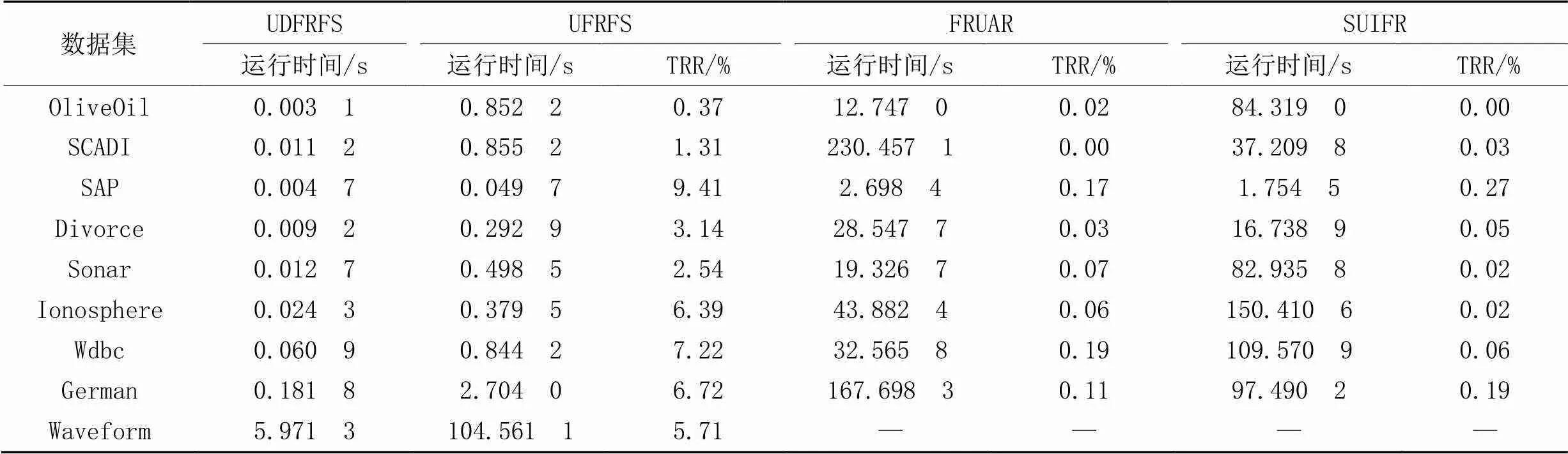
表3　不同大小增量数据集上不同算法的运行时间对比

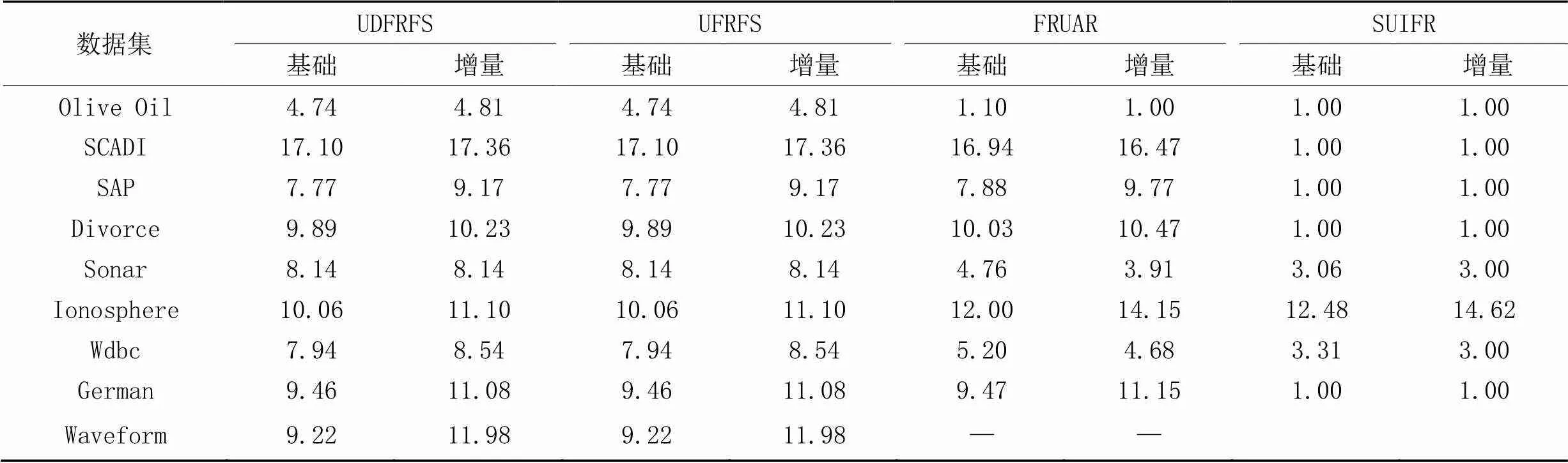
表4　不同算法的特征子集大小对比

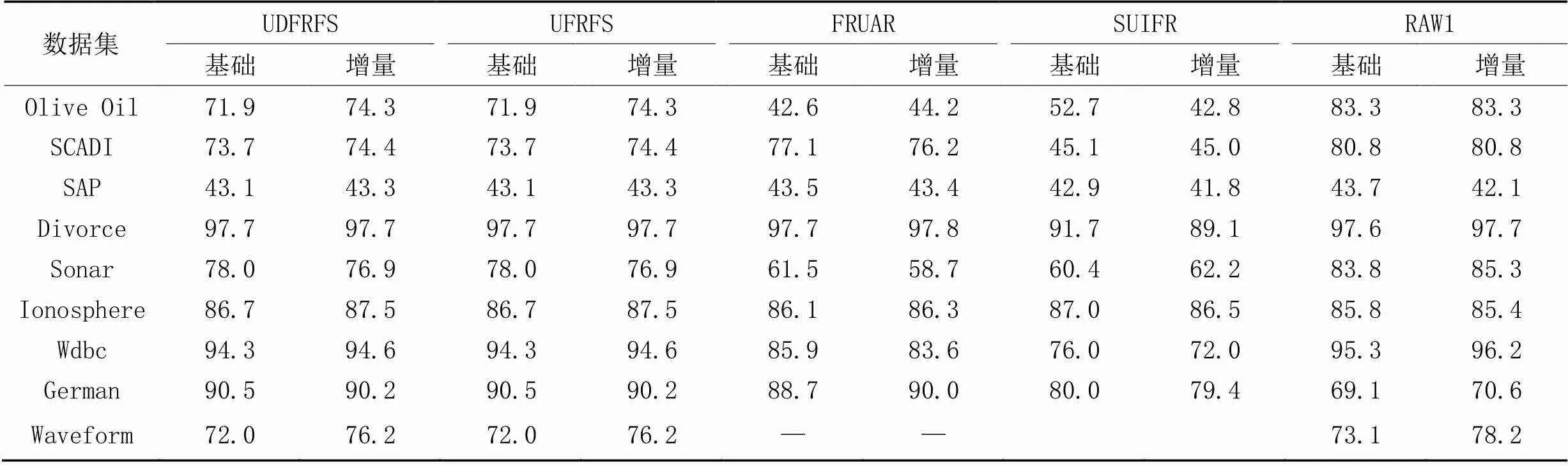
表5　不同算法在KNN下的分类精度对比 单位：%

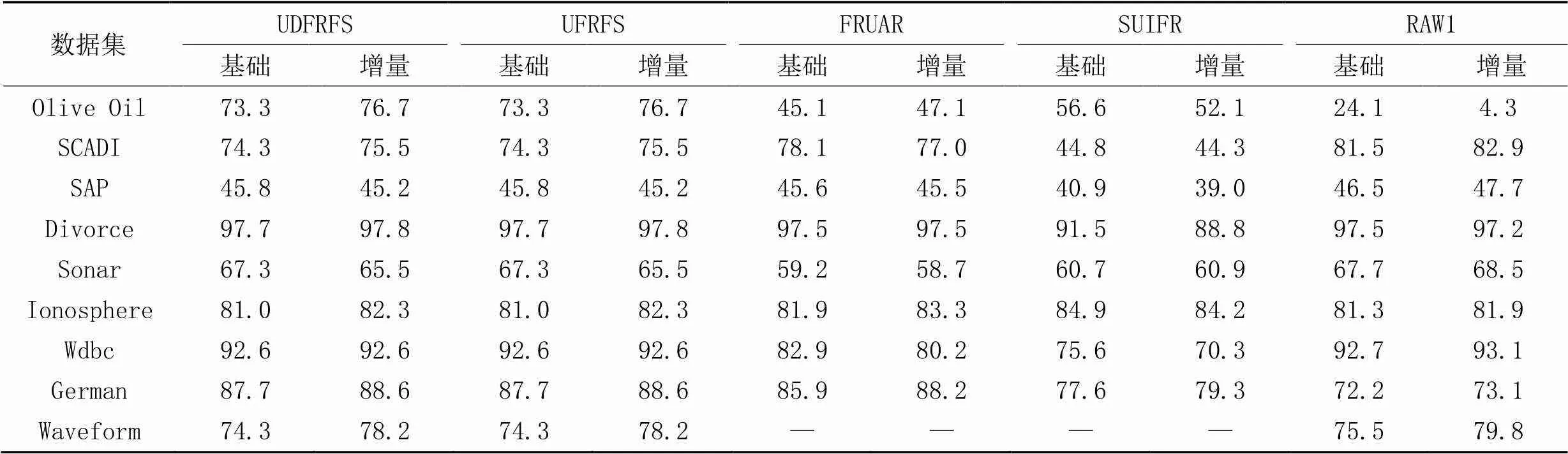
表6　不同算法在NB下的分类精度对比 单位：%

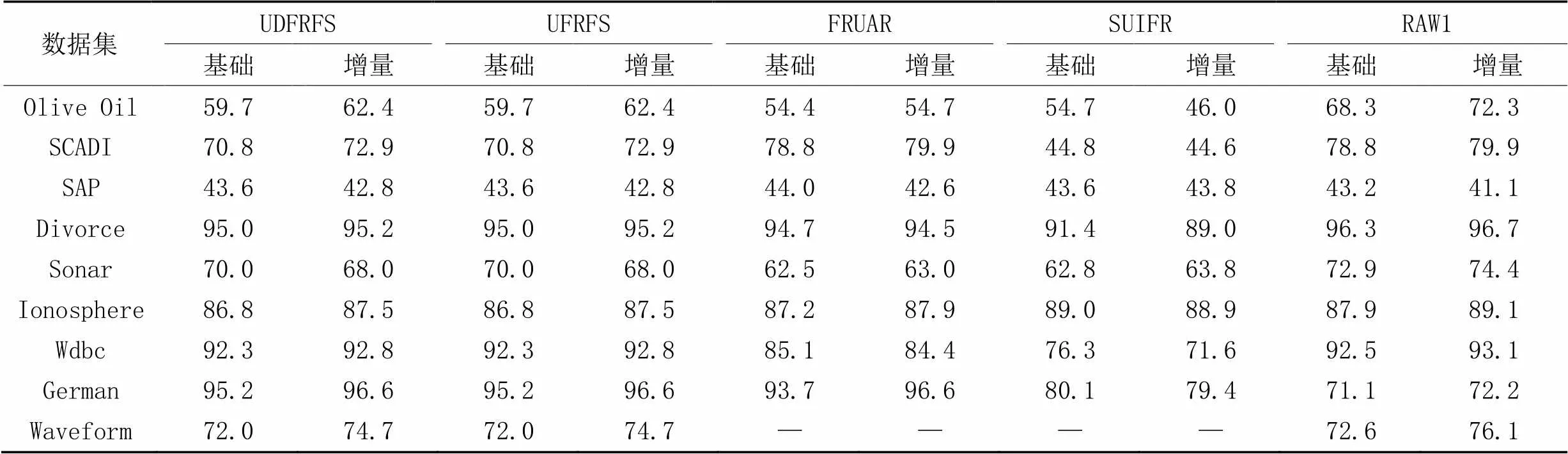
表7　不同算法在CART下的分类精度对比 单位：%

3.3.3聚类表现

作为无监督特征选择算法，有必要对比它们在聚类算法下的表现。本节选用对数似然（log likelihood）作为评价指标。使用的数据集的基本属性如表1所示。

表8为不同算法在不同大小基础数据集和不同大小增量数据集上的对数似然对比，“RAW2”表示没有经过特征选择的原始数据集的对数似然。从表8的实验结果可以看出，除了少部分数据集（如SAP和Wdbc），在大部分数据集上使用这几种特征选择算法，聚类质量均有不同程度的提高。在Olive Oil上，虽然UDFRFS和UFRFS得到的特征选择后的数据集完全一样，但个别实验结果存在差异，导致最后的平均结果有所不同，推测原因是计算过程中产生了误差。

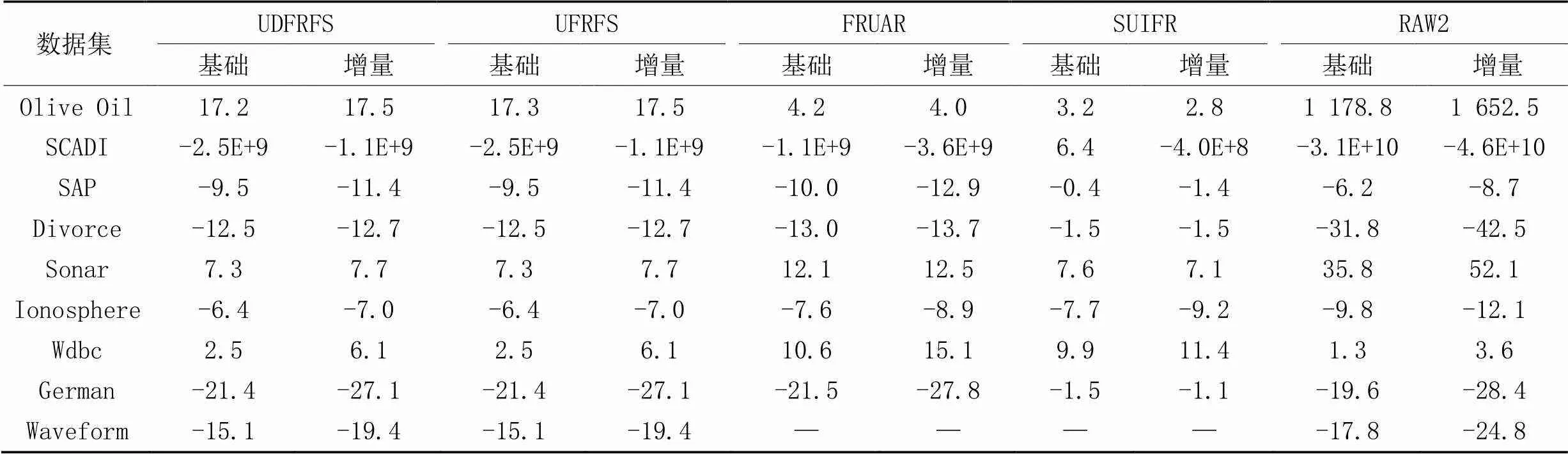
表8　不同算法在各数据集上的对数似然对比

4 结语

本文提出了一种特征分批次到达情况下基于模糊粗糙集的无监督动态特征选择算法，该算法通过定义伪三角范数和新的相似关系，从而加快无监督动态特征选择算法中模糊关系值和依赖度的计算过程，使得算法在特征分批次到达的情况下能在保证较好的特征选择效果、分类精度和聚类表现的情况下大幅提升算法的时间效率，并在针对特征增加这一类型的动态数据集上取得了一定效果。未来将把该特征选择算法应用在其他类型的动态数据集上，探索在特征减少、样本增加、样本减少和特征值改变等情况下的可行性，使得算法具有更好的可扩展性。此外，将进一步在保证算法的执行效率不受影响的情况下，提升该算法的特征选择质量，使得经过该算法选择得到的特征子集更小，经过特征选择后的数据集也能够获得更高的分类精度和更好的聚类性能。

[1] PAWLAK Z. Rough sets［J］. International Journal of Computing and Information Sciences， 1982， 11（5）： 341-356.

[2] DUBOIS D， PRADE H. Rough fuzzy sets and fuzzy rough sets［J］. International Journal of General Systems， 1990， 17（2/3）： 191-209.

[3] ZADEH L A. Fuzzy sets［J］. Information and Control， 1965， 8（3）： 338-353.

[4] AN S， LIU J， WANG C， et al. A relative uncertainty measure for fuzzy rough feature selection［J］. International Journal of Approximate Reasoning， 2021， 139： 130-142.

[5] CHEN J， MI J， LIN Y. A graph approach for fuzzy-rough feature selection［J］. Fuzzy Sets and Systems， 2020， 391： 96-116.

[6] YANG X， CHEN H， LI T， et al. A noise-aware fuzzy rough set approach for feature selection［J］. Knowledge-Based Systems， 2022， 250： No.109092.

[7] 章夏杰，朱敬华，陈杨. Spark下的分布式粗糙集属性约简算法［J］. 计算机应用， 2020， 40（2）： 518-523.（ZHANG X J， ZHU J H， CHEN Y. Distributed rough set attribute reduction algorithm under Spark［J］. Journal of Computer Applications， 2020， 40（2）： 518-523.）

[8] 危前进，魏继鹏，古天龙，等. 粗糙集多目标并行属性约简算法［J］. 软件学报， 2022， 33（7）： 2599-2617.（WEI Q J， WEI J P， GU T L， et al. Multi-objective parallel attribute reduction algorithm in rough set［J］. Journal of Software， 2022， 33（7）： 2599-2617.）

[9] YANG Y， CHEN D， WANG H， et al. Fuzzy rough set based incremental attribute reduction from dynamic data with sample arriving［J］. Fuzzy Sets and Systems， 2017， 312： 66-86.

[10] WAN J， CHEN H， LI T， et al. Dynamic interaction feature selection based on fuzzy rough set［J］. Information Sciences， 2021， 581： 891-911.

[11] NI P， ZHAO S， WANG X， et al. Incremental feature selection based on fuzzy rough sets［J］. Information Sciences， 2020， 536： 185-204.

[12] 程玉胜，陈飞，王一宾. 基于粗糙集的数据流多标记分布特征选择［J］. 计算机应用， 2018， 38（11）： 3105-3111， 3118.（CHENG Y S， CHEN F， WANG Y B. Feature selection for multi-label distribution learning with streaming data based on rough set［J］. Journal of Computer Applications， 2018， 38（11）： 3105-3111， 3118.）

[13] 曾艺祥，林耀进，范凯钧，等. 基于层次类别邻域粗糙集的在线流特征选择算法［J］. 南京大学学报（自然科学版）， 2022， 58（3）： 506-518.（ZENG Y X， LIN Y J， FAN K J， et al. Online streaming feature selection method based on hierarchical class neighborhood rough set［J］. Journal of Nanjing University （Natural Sciences）， 2022， 58（3）： 506-518.）

[14] SOLORIO-FERNÁNDEZ S， CARRASCO-OCHOA J A， MARTÍNEZ-TRINIDAD J F. A review of unsupervised feature selection methods［J］. Artificial Intelligence Review， 2020， 53（2）： 907-948.

[15] VELAYUTHAM C， THANGAVEL K. Unsupervised quick reduct algorithm using rough set theory［J］. Journal of Electronic Science and Technology， 2011， 9（3）： 193-201.

[16] VELAYUTHAM C， THANGAVEL K. A novel entropy based unsupervised feature selection algorithm using rough set theory［C］// Proceeding of the 2012 International Conference on Advances in Engineering， Science and Management. Piscataway： IEEE， 2012： 156-161.

[17] MAC PARTHALÁIN N， JENSEN R. Unsupervised fuzzy-rough set-based dimensionality reduction［J］. Information Sciences， 2013， 229： 106-121.

[18] YUAN Z， CHEN H， LI T， et al. Unsupervised attribute reduction for mixed data based on fuzzy rough sets［J］. Information Sciences， 2021， 572： 67-87.

[19] GANIVADA A， RAY S S， PAL S K. Fuzzy rough sets， and a granular neural network for unsupervised feature selection［J］. Neural Networks， 2013， 48： 91-108.

[20] BEG I， ASHRAF S. Similarity measures for fuzzy sets［J］. Applied and Computational Mathematics， 2009， 8（2）： 192-202.

[21] PAP E. Pseudo-analysis in engineering decision making［M］// RUDAS I J， FODOR J， KACPRZYK J. Towards Intelligent Engineering and Information Technology， SCI 243. Berlin： Springer， 2009： 3-16.

[22] WANG L， PENG L， ZHANG G. Attribute reduction for incomplete and unsupervised data based on fuzzy rough sets［C］// Proceeding of the 16th International Conference on Intelligent Systems and Knowledge Engineering. Piscataway： IEEE， 2021： 674-679.

Fuzzy-rough set based unsupervised dynamic feature selection algorithm

MA Lei1， LUO Chuan1*， LI Tianrui2， CHEN Hongmei2

（1，，610065，；2，，611756，）

Dynamic feature selection algorithms can improve the time efficiency of processing dynamic data. Aiming at the problem that there are few unsupervised dynamic feature selection algorithms based on fuzzy-rough sets， an Unsupervised Dynamic Fuzzy-Rough set based Feature Selection （UDFRFS） algorithm was proposed under the condition of features arriving in batches. First， by defining a pseudo triangular norm and new similarity relationship， the process of updating fuzzy relation value was performed on the basis of existing data to reduce unnecessary calculation. Then， by utilizing the existing feature selection results， dependencies were adopted to judge if the original feature part would be recalculated to reduce the redundant process of feature selection， and the feature selection was further speeded up. Experimental results show that compared to the static dependency-based unsupervised fuzzy-rough set feature selection algorithm， UDFRFS can achieve the time efficiency improvement of more than 90 percentage points with good classification accuracy and clustering performance.

feature selection; fuzzy-rough set; dynamic data; unsupervised feature selection; dependency

This work is partially supported by National Natural Science Foundation of China （62076171）， Natural Science Foundation of Sichuan Province （2022NSFSC0898）.

MA Lei， born in 1997， M. S. candidate. His research interests include feature selection.

LUO Chuan， born in 1987， Ph. D.， associate professor. His research interests include data mining， granular computing.

LI Tianrui， born in 1969， Ph. D.， professor. His research interests include data mining， granular computing.

CHEN Hongmei， born in 1971， Ph. D.， professor. Her research interests include data mining， granular computing.

1001-9081（2023）10-3121-08

10.11772/j.issn.1001-9081.2022101543

2022⁃10⁃17；

2022⁃11⁃28；

国家自然科学基金资助项目（62076171）；四川省自然科学基金资助项目（2022NSFSC0898）。

马磊（1997—），男（回族），四川成都人，硕士研究生，主要研究方向：特征选择； 罗川（1987—），男，河南固始人，副教授，博士，主要研究方向：数据挖掘、粒计算； 李天瑞（1969—），男，福建莆田人，教授，博士，CCF会员，主要研究方向：数据挖掘、粒计算； 陈红梅（1971—），女，四川成都人，教授，博士，CCF会员，主要研究方向：数据挖掘、粒计算。

TP301.6

A

2022⁃11⁃30。