基于特征融合图注意网络的高速公路交通流预测

高醇，王梦灵

基于特征融合图注意网络的高速公路交通流预测

高醇，王梦灵*

（华东理工大学 信息科学与工程学院，上海 200237）（ ∗ 通信作者电子邮箱wml_ling@ecust.edu.cn）

基于交通网络的实际时空拓扑，提出一种特征融合图注意网络（FF-GAT）模型融合节点获取的多种交通状态信息，预测高速公路交通流。首先，分析节点的车速、交通流和占有率之间的关联特征，并基于多变量时间注意力机制，将车速、交通流和占有率之间的关系融入注意力机制，从而捕捉交通流的不同时间之间的动态时间相关性；其次，将节点划分为不同的邻域集，并通过特征融合图注意网络（GAT）捕获交通流的不同邻域之间的空间相关性；同时，通过特征交叉网络充分挖掘多个异构数据之间的耦合相关性，为预测目标序列提供有效的信息补充。在两个公开交通流数据集上的实验结果表明：在PeMSD8数据集上，与ASTGCN（Attention based Spatial-Temporal Graph Convolutional Network）模型相比，FF-GAT模型的均方根误差（RMSE）降低了3.4%；与GCN-GAN（Graph Convolutional Network and Generative Adversarial Network）模型相比，FF-GAT模型的RMSE降低了3.1%。可见，FF-GAT模型能够通过特征融合有效提高预测精度。

高速公路交通流预测；图注意网络；注意力机制；特征交叉网络；时空拓扑

0 引言

准确的交通预测可以帮助交通管理部门制定合适的控制策略，更合理地引导车辆，有效缓解交通拥堵。与地面道路和城市快速路相比，高速公路具有特定的交通模式。高速公路的车辆行驶速度快且不间断，一旦发生拥堵或者交通事故，将严重影响通行能力。因此，预测高速公路的交通状态，及时发现交通状态的变化，辅助交通治理十分重要［1-3］。

交通状态随时间和空间发生改变，可以根据交通网络的地理位置划分为不同的网格图［4-5］。对于高速公路的交通网络，可以将公路上不同位置布设的传感器作为节点，传感器间的信息连通作为边，交通流、平均车速、占有率等交通状态参数作为测量数据的属性。针对交通网络的图结构表征，许多研究采用图卷积模型聚合交通网络节点的信息，通过捕捉节点之间的空间依赖关系，从整个图结构预测所有节点交通状态变化。文献［6-8］中采用卷积神经网络、循环神经网络模拟时序关联，同时采用图卷积模拟空间关联；但图卷积在卷积过程中无法根据相邻节点的重要性分配不同的权值，每个节点权重相同，影响预测精度。近年来，一些通过引入注意力机制考虑交通数据在时间和空间维度上的动态关联性，计算不同场景中时空节点的相互影响程度。Zhu等［9］在时间图卷积网络（Temporal Graph Convolutional Network， T-GCN）［8］中引入时间注意力机制，调整不同时间点的重要性，基于该改进方法交通状态变化预测精度更高。Guo等［10］分析交通流的近期相关性、日周期相关性和周周期相关性，先将交通流进行时间注意力机制处理，再在空间图卷积中加入注意力机制（时间和空间上的注意力机制计算公式相同），设计时空图卷积模型预测交通状态的变化。事实上，特定位置的异构数据直接影响预测序列。Liang等［11］设计气象等外部因素抽取模块输入到局部空间和全局空间注意力机制，捕获不同传感器之间的动态空间相关性。Yin等［12］提出的多阶段注意力机制能捕获同一传感器采集的多个时间序列之间的交互作用。

由于基于图卷积的交通预测模型属于频域（spectral domain）派别，主要通过引入滤波器定义图卷积，其中图卷积操作被解释为从图信号中去除噪声，需要进行拉普拉斯矩阵特征分解［13-14］，计算量较大。其次，由于高速公路网络结构复杂，道路网络中不同节点对目标节点的影响不同，随着时间的推移，影响权重高度复杂，且是动态的。图卷积的模型训练依赖对全图所有节点的预先访问，泛化能力弱，无法实现归纳性学习。最后，多层图卷积存在过平滑问题，在使用多层图卷积后，节点的表示向量趋于一致，使得相应的学习任务变得更加困难。针对以上问题，Veličković等［15］提出了图注意网络（Graph Attention neTwork， GAT），GAT属于空域（vertex domain）派别，无须代价高昂的矩阵计算，计算量较小。图注意模型自主地学习一阶邻域中邻居节点对目标节点的重要性，自适应分配不同邻居的空间权重，更好地解决了基于频域图卷积的问题。当预测路网交通状态时，需要准确计算路网节点影响系数，但图注意网络仅考虑周围有限节点对目标节点的交互影响，未考虑路网结构的多阶邻接关系，信息利用不充分，而且也没有加入多变量的信息。

针对上述问题，本文提出一种基于特征融合图注意网络（Feature Fusion Graph ATtention network， FF-GAT）模型。将平均车速和占有率作为多变量，在时间维度上分别把车速、占有率对交通流的相关度函数引入时间注意力机制，增强模型刻画时序上特征相关性的能力；为了更好地挖掘不同节点之间隐含空间相关性，构建一阶邻接矩阵和二阶邻接矩阵，将它们输入图注意网络，计算不同邻域对目标节点的影响系数，线性组合后增大空间维度感受野；基于图注意网络引入特征交叉捕捉不同变量的交叉关系，抓取每个节点变量的特征信息；结合二维卷积网络和特征融合图注意网络，模拟时空关联。本文模型生成的预测结果与真实路网交通流分布基本一致，预测准确率较高，同时消融实验和参数敏感性分析验证了模型的有效性。

1 问题描述

假设高速公路的交通状态可以由个传感器测得，具体可以表示为矩阵如下：

一般地，对于每一个传感器（即节点）测量的不同的交通状态变量，交通流、平均车速和道路占有率三者之间的关联关系可以表示为式（2）～（3）［16］。

2）⁃关系。

其中：为映射函数；为预测窗口长度。

虽然交通状态变量之间的关系可以由常用的线性模型表示，但是高速公路网络结构复杂，而且交通状态是时变的，交通流计算结果与实际测量结果不一致，因此不能采用单一的模型描述。本文按照时空的推移寻找三者的关联关系，在空间上尽可能挖掘图结构的状态信息，采取二阶图注意网络的模型预测交通流。

2 特征融合图注意网络模型

2.1　FF-GAT模型的总体架构

FF-GAT模型的总体架构如图1（a）所示，它主要由多层时空层组成。时空层由多变量时间注意力机制、特征交叉图注意网络和时间二维卷积串联组成，串联堆叠多个时空层，每个时空层采用残差学习的方式训练，最后接入一个多层感知机模型输出层。

如图1（b），在第一个虚线框中构建多变量时间注意力机制，利用平均车速、占有率和交通流的相关度函数，融合计算各时刻流程状态重要性，增强模型在时序上特征相关性的刻画能力；在第二个虚线框中同时创建一阶邻接矩阵和二阶邻接矩阵，输入图注意网络，计算不同邻域对目标节点的影响系数，增强路网节点的空间相关性，在图注意网络基础上引入特征交叉挖掘每个节点的不同交通状态关系；在第三个虚线框中利用二维卷积网络提取时域上的特征信息，通过一层时空层操作后，可以捕获交通流的时间维和空间维特征。

图1　本文模型架构

2.2　多变量时间注意力机制

在时间域上，不同时刻路网节点的交通流之间也存在相关性，且这种时间相关性随着路网条件的变化而变化。文献［10］中利用注意力机制为不同时刻路网交通流赋予不同重要性，时间域上的时间注意力机制如下：

对于交通网络中的某个节点，记录不同的时间序列，如交通流、速度和占有率。同一节点的这3个变量在不同时刻之间存在着相关性，由于式（2）～（3）是线性关系模型，数学形式简单，对实际数据的拟合效果较差，不能用式（2）～（3）表示三者之间的关联关系。因此，对于实际数据，借助余弦相似度（式（6））分别计算平均车速和占有率对交通流的相似度：

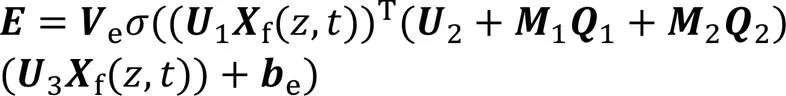
图2　多变量时间注意力机制

2.3　基于图注意网络的空间特征

与一般忽略路网结构信息的基于注意的方法相比，本文所提图注意网络不需要在图卷积基础上进行注意力机制处理［10］，可以直接自适应地分配不同邻居的空间权重，采用邻接关系作为先验，将节点划分为两个邻域集；其次，利用注意力机制同时动态捕捉第一阶邻域和第二阶邻域间的空间相关性；最后，对观测节点的邻域节点特征进行加权求和，提取目标节点的特征信息和不同邻域对它的影响。

2.3.1构建邻接矩阵

传统的邻接矩阵主要关注直接连接的节点，即相邻的一阶邻居，而忽略了节点之间的间接连接。如图3所示，本文采用新的邻接矩阵编码传感器之间的直接邻接关系和间接邻接关系。

其中为i到j的最短路径长度。

2.3.2二阶邻域图注意网络

图4　图注意力层

（=1，2）阶邻域的注意力系数的计算公式如下：

每个节点的最终输出特征如下：

为了稳定自注意力学习过程，进一步提升注意力层的表达能力，对最终的网络层执行多头注意力机制：

其中表示注意力头数。

图5　二阶邻域图注意网络

2.4　多变量输入特征交叉

图6　特征交叉

第+1层的交叉过程如下：

通过多层网络对特征向量各个维度进行充分的交叉组合，模型能够抓取更多的非线性特征和组合特征的信息，此外，特征交叉网络还有低线性复杂度和参数共享的优点。

2.5　基于二维卷积的时空状态预测

本文利用标准二维卷积提取时域上的特征，具体做法是对每个节点自身时间域上的相邻点进行卷积操作。经过空间特征提取和时间特征提取后的结果如下：

2.6　算法训练步骤

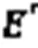
步骤3 多个串联堆叠的时空层采用残差学习的方式训练，输出的交通流接入全连接层。

3 实验与结果分析

3.1　实验数据集

为了验证本文模型的性能和有效性，在两个数据集（PeMSD4和PeMSD8）上进行对比实验。两个数据集是从加州交通性能测量系统（PeMS）［17］收集：PeMSD4包含了美国加州旧金山湾区（San Francisco Bay Area）的路网节点交通状态数据，PeMSD8包含了美国加州圣贝纳迪诺县（San Bernardino）的路网节点交通状态数据。为了方便研究，本文中所用的数据集都移除了路网节点中的冗余检测点，确保数据集中每个节点都不过于接近（相邻节点间的距离不大于3.5 英里（1 英里=1.61 km））。最终得到的PeMSD4和PeMSD8分别包含了307个节点和170个节点，同时聚集原有每隔30 s的采样数据，使得每条样本数据间的间隔为5 min。本文利用平均值插值法补全缺失数据，利用零均值对输入数据归一化。实验考虑3个输入特征：交通流、平均车速和占用率，并将数据集按照6∶2∶2随机分割为训练集、验证集和测试集。

3.2　评价指标

本文选择均方根误差（Root Mean Squared Error， RMSE）和平均绝对误差（Mean Absolute Error， MAE）作为评价指标，它们的计算公式分别为：

3.3　模型对照基线

选用长短期记忆（Long Short-Term Memory， LSTM）网络［18］、时空图卷积网络（Spatio-Temporal Graph Convolutional Network， STGCN）［19］、GeoMAN（Multi-level Attention Network for Geo-sensory time series prediction）模型［11］、ASTGCN（Attention based Spatial-Temporal Graph Convolutional Network）模型［10］、GCN-GAN（Graph Convolutional Network and Generative Adversarial Network）模型［20］作为实验对比的基线。同时，为了和传统非深度学习模型进行比较，本文选取了历史平均（Historical Average， HA）、向量自回归（Vector Auto-Regressive， VAR）［21］和差分整合移动平均自回归（AutoRegressive Integrated Moving Average， ARIMA）模型［22］作为传统基线模型。在HA中，根据前12个时间片的平均值预测下一个值。

根据相关文献和历史经验设定上述基准模型的关键参数，分别如下：ARIMA模型的自回归系数为4，移动平均项数为2，差分阶数为2；VAR的最佳滞后阶数为3；LSTM的网络层数为2，隐藏层数为64；STGCN［19］、GeoMAN模型［11］、ASTGCN模型［10］和GCN-GAN模型［20］的参数设置均参考相应文献，设置为默认值。

3.4　参数设置

经过测试和验证，时间维的卷积核大小不能过大，本文时间维卷积核的大小设置为（1，3），图注意力网络中的多头注意力头数设置为2，图注意网络中隐藏层维度设置为64，本文的预测步长大小置为12，即预测未来1 h的路网节点流量。利用Adam优化器训练，批处理大小设置为32，初始学习率设置为0.001，训练的最大迭代数设置为100。

在本文建立的预测模型中，主要有3个影响模型预测性能的超参数，分别是注意力头数、邻域阶数和隐藏层维度，其中：注意力头数影响注意力层的权重计算复杂度；邻域阶数影响图结构中邻居节点信息的聚合程度；隐藏层维度影响神经网络的拟合函数能力。在PeMSD4和PeMSD8数据集上，设置注意力头数为｛1，2，3，4｝，邻域阶数为｛1，2，3，4｝，隐藏层维度｛16，32，64，128｝，使用试凑法分别测试3个参数对模型的影响。

注意力头数、邻域阶数对模型性能的影响如图7所示。随着头数增加，模型的误差先降低再升高，当头数为2时误差最小，当头数过大时，模型可能出现过拟合。随着邻域阶数增加，在一阶邻域时模型不能提取更完善的信息；在二阶邻域时模型可以很好地聚合信息，此时模型误差最小；继续加深邻域阶数，可能降低信息区分度，导致误差较大。

图7　不同超参数在不同数据集上的预测误差对比

3.5　实验结果与分析

表1为不同模型在PeMSD4和PeMSD8数据集上在路网节点未来60 min的流量预测平均结果。从表1可以看出，在PeMSD4和PeMSD8数据集上，与4个经典时间序列模型相比，FF-GAT模型的RMSE分别降低了22.4%～47.8%和12.9%～38.2%，可以看出，经典时间序列模型的预测结果较差，这可能是因为经典时间序列模型对非线性的复杂交通数据建模能力有限，而深度学习模型对复杂的路网预测能力更强。对比不同的深度学习模型，STGCN、GeoMAN和FF-GAT模型都同时提取了时间和空间特征，在PeMSD4和PeMSD8数据集上，FF-GAT模型的RMSE与STGCN相比分别降低了7.4%和11.7%，与GeoMAN相比分别降低了6.0%和5.9%，与ASTGCN相比分别降低了2.0%和3.4%，与GCN-GAN相比分别降低了1.9%和3.1%。本文模型对路网的预测结果更理想，同时由于本文模型在特征提取时更全面地挖掘了节点拓扑信息，因此在两个数据集上的预测结果精度都较好。

表1　不同模型在PeMSD4和PeMSD8数据集上的结果对比

图8为9种模型的预测精度指标（RMSE和MAE）随着预测时间的变化曲线。从图8可以看出，随着预测时间的增加，HA、ARIMA、LSTM的预测精度急剧下降，VAR的精度略慢于上述3种模型，深度学习模型的误差随着预测时间的增加而缓慢增加，总体性能良好。从图8可以看出，当时间为60 min时，在两个数据集上，FF-GAT模型的RMSE均低于其他对比模型。与上述模型相比，ASTGCN通过引入注意力机制处理时空动态特性，预测精度有所提升，本文模型在时间和空间维度都考虑了多变量的参数影响，充分考虑了交通流数据的时空相关性，因此能达到最佳的预测性能。

图8　不同模型在不同预测时长下的性能比较

FF-GAT模型在PeMSD4数据集上对176号传感器预测的交通流与实际值的差异曲线如图9（a）所示，在PeMSD8数据集上对3号传感器预测的交通流与实际值的差异曲线如图9（b）所示。基于真实值的曲线非常不规则，但本文模型大致符合趋势，说明FF-GAT模型对数据中可能的模式有更强的学习能力，这也说明了本文模型的有效性。

图9　FF-GAT模型的交通流量预测值与真实值的对比

FF-GAT模型参数拟合过程中的误差变化曲线如图10所示，随着迭代次数（epoch）的增加，预测精度逐渐升高，误差值逐渐减小，模型收敛较快。在PeMSD4数据集上，在迭代次数为40时模型趋于稳定，观察验证集发现迭代次数为78时模型参数误差最小；同样地，在PeMSD8数据集上，模型在迭代次数为45时趋于稳定，观察验证集发现迭代次数为74时模型参数误差最小，以上结果说明了本文模型的稳定性。

图10　FF-GAT模型的误差曲线

3.6　消融实验

为了验证本文模型中各个模块的有效性，设计两个变体模型：1）MA，即移除多变量时间注意力机制模块；2）MF，即移除多变量输入特征交叉模块。消融实验结果见表2，可以看出，两个变体模型的误差均高于FF-GAT模型，表明模型的各个组件的有效性，多变量时间注意力机制能为模型在时间维度上提供更多信息辅助模型预测，多变量输入特征交叉也能更好地挖掘交通数据中的相关性。

表2　不同模块在PeMSD4和PeMSD8数据集上的性能

4 结语

高速公路交通流预测是现代交通管理的一个基本问题。针对采集的路网状态具有时空复杂性和非线性特征的问题，本文提出一种基于特征融合图注意网络的路网交通流预测模型。在时间上考虑交通预测中同一节点不同交通变量之间的关系，利用多变量时间注意力机制捕捉不同时间之间的动态时间相关性；在空间上以路网不同邻域信息为先验，利用二阶图注意网络捕获网络内部的综合空间相关性，再用多变量特征交叉网络充分挖掘多个异构数据之间的耦合相关性，为预测交通流提供有效的信息补充。在两个PeMS数据集上的实验结果表明，所提模型与现有对比模型相比，在挖掘特征和预测精度方面均具有一定优势。下一步将收集道路功能特征、天气特征、节假日和社会事件等数据集，为用户提供最全面的信息，形成完整的智能交通系统，促进智慧城市交通的发展。

[1] CHEN L， SHAO W， LV M， et al. AARGNN： an attentive attributed recurrent graph neural network for traffic flow prediction considering multiple dynamic factors［J］. IEEE Transactions on Intelligent Transportation Systems， 2022， 23（10）： 17201-17211.

[2] SHIN Y， YOON Y. Incorporating dynamicity of transportation network with multi-weight traffic graph convolutional network for traffic forecasting［J］. IEEE Transactions on Intelligent Transportation Systems， 2022， 23（3）： 2082-2092.

[3] HUANG J， LUO K， CAO L， et al. Learning multiaspect traffic couplings by multirelational graph attention networks for traffic prediction［J］. IEEE Transactions on Intelligent Transportation Systems， 2022， 23（11）： 20681-20695.

[4] 王海起，王志海，李留珂，等. 基于网格划分的城市短时交通流量时空预测模型［J］. 计算机应用， 2022， 42（7）：2274-2280.（WANG H Q， WANG Z H， LI L K， et al. Spatial-temporal prediction model of urban short-term traffic flow based on grid division［J］. Journal of Computer Applications， 2022， 42（7）：2274-2280.）

[5] LIN Z， FENG J， LU Z， et al. DeepSTN+： context-aware spatial-temporal neural network for crowd flow prediction in metropolis［C］// Proceedings of the 33rd AAAI Conference on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2019： 1020-1027.

[6] 陈丹蕾，陈红，任安虎. 考虑时空影响下的图卷积网络短时交通流预测［J］. 计算机工程与应用， 2021， 57（13）：269-275.（CHEN D L， CHEN H， REN A H. Short-time traffic flow prediction of graph convolutional network considering influence of space and time［J］. Computer Engineering and Applications， 2021， 57（13）：269-275.）

[7] SONG C， LIN Y， GUO S， et al. Spatial-temporal synchronous graph convolutional networks： a new framework for spatial-temporal network data forecasting［C］// Proceedings of the 34th AAAI Conference on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2020： 914-921.

[8] ZHAO L， SONG Y， ZHANG C， et al. T-GCN： a temporal graph convolutional network for traffic prediction［J］. IEEE Transactions on Intelligent Transportation Systems， 2020， 21（9）： 3848-3858.

[9] ZHU J， HAN X， DENG H， et al. KST-GCN： a knowledge-driven spatial-temporal graph convolutional network for traffic forecasting［J］. IEEE Transactions on Intelligent Transaction Systems， 2022， 23（9）： 15055-15065.

[10] GUO S， LIN Y， FENG N， et al. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting［C］// Proceedings of the 33rd AAAI Conference on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2019： 922-929.

[11] LIANG Y， KE S， ZHANG J， et al. GeoMAN： multi-level attention networks for geo-sensory time series prediction［C］// Proceedings of the 27th International Joint Conference on Artificial Intelligence. California： ijcai.org， 2018： 3428-3434.

[12] YIN X， WU G， WEI J， et al. Multi-stage attention spatial-temporal graph networks for traffic prediction［J］. Neurocomputing， 2021， 428： 42-53.

[13] DEFFERRARD M， BRESSON X， VANDERGHEYNST P. Convolutional neural networks on graphs with fast localized spectral filtering［C］// Proceedings of the 30th International Conference on Neural Information Processing Systems. Red Hook， NY： Curran Associates Inc.， 2016： 3844-3852.

[14] BRUNA J， ZAREMBA W， SZLAM A， et al. Spectral networks and locally connected networks on graphs［EB/OL］. （2014-05-21） ［2022-05-23］.https：//arxiv.org/pdf/1312.6203.pdf.

[15] VELIČKOVIĆ P， CUCURULL G， CASANOVA A， et al. Graph attention networks［EB/OL］. （2018-02-04） ［2022-05-23］.https：//arxiv.org/pdf/1710.10903.pdf.

[16] GREENSHIELDS B D， BIBBINS J R， CHANNING W S， et al. A study of traffic capacity［J］. Highway Research Board Proceedings， 1935， 14： 448-477.

[17] CHEN C， PETTY K， SKABARDONIS A， et al. Freeway performance measurement system： mining loop detector data［J］. Transportation Research Record， 2001， 1748（1）： 96-102.

[18] HOCHREITER S， SCHMIDHUBER J. Long short-term memory［J］. Neural Computation， 1997， 9（8）： 1735-1780.

[19] YU B， YIN H， ZHU Z. Spatio-temporal graph convolutional networks： a deep learning framework for traffic forecasting［C］// Proceedings of the 27th International Joint Conference on Artificial Intelligence. California： ijcai.org， 2018：3634-3640.

[20] ZHENG H， LI X， LI Y， et al. GCN-GAN： integrating graph convolutional network and generative adversarial network for traffic flow prediction［J］. IEEE Access， 2022， 10： 94051-94062.

[21] SETHI J K， MITTAL M. Analysis of air quality using univariate and multivariate time series models［C］// Proceedings of the 10th International Conference on Cloud Computing， Data Science and Engineering. Piscataway： IEEE， 2020： 823-827.

[22] RUN L， MIN L X， LU Z X. Research and comparison of ARIMA and grey prediction models for subway traffic forecasting［C］// Proceedings of the 2020 International Conference on Intelligent Computing， Automation and Systems. Piscataway： IEEE， 2020：63-67.

Highway traffic flow prediction based on feature fusion graph attention network

GAO Chun， WANG Mengling*

（，，200237，）

Based on the actual spatio-temporal topology of the traffic network， a Feature Fusion Graph ATtention network （FF-GAT） model was proposed to fuse multiple traffic state information obtained by nodes， so as to predict the highway traffic flow. First， the correlation features among the vehicle speed， traffic flow and occupancy of the nodes were analyzed， and based on the multivariate temporal attention mechanism， the relationships among the vehicle speed， traffic flow and occupancy were incorporated into the attention mechanism to capture the dynamic temporal correlation between different moments of traffic flow. Then， the nodes were divided into different sets of neighborhoods， and the spatial correlation between different neighborhoods of traffic flow was captured by the feature fusion Graph Attention neTwork （GAT）. At the same time， the coupling correlation between multiple heterogeneous data was fully explored by the feature crossover network to provide effective information supplement for predicting the target sequence. Experiments were carried out on two publicly available traffic flow datasets. Experimental results show that FF-GAT model reduces the Root Mean Squared Error （RMSE） by 3.4% compared with ASTGCN （Attention based Spatial-Temporal Graph Convolutional Network） model and 3.1% compared with GCN-GAN （Graph Convolutional Network and Generative Adversarial Network） model on PeMSD8 dataset. It can be seen that FF-GAT model can effectively improve the prediction accuracy through feature fusion.

highway traffic flow prediction; Graph Attention neTwork (GAT); attention mechanism; feature crossover network; spatio-temporal topology

This work is partially supported by Project of Science and Technology Commission of Shanghai Municipality （19DZ1209003）.

GAO Chun， born in 1998， M. S. candidate. Her research interests include traffic big data mining.

WANG Mengling， born in 1980， Ph. D.， associate professor. Her research interests include traffic big data mining， computational intelligence algorithm， artificial intelligence-based modeling method， distributed predictive control， traffic management decision optimization.

1001-9081（2023）10-3114-07

10.11772/j.issn.1001-9081.2022101587

2022⁃10⁃24；

2023⁃03⁃13；

上海市科学技术委员会课题（19DZ1209003）。

高醇（1998—），女，云南曲靖人，硕士研究生，主要研究方向：交通大数据挖掘； 王梦灵（1980—），女，湖北黄冈人，副教授，博士，主要研究方向：交通大数据挖掘、计算智能算法、基于人工智能的建模方法、分布式预测控制、交通管理决策优化。

TP391.4

A

2023⁃03⁃14。