基于多级优化的圆拟合算法
徐永亮,谢小辉
(苏州大学 机电工程学院,江苏 苏州 215000)
圆拟合是图像处理中一种常见的检测形式,多次出现在工业现场等实际场景中。检测算法的准确度、运行时间及稳定性是评价拟合圆算法性能的重要指标[1]。常见的圆拟合算法主要有标准Hough变换和最小二乘法(Least Squares,LS)。Hough变换将参数映射到三维空间,计算量大、耗时长且需要较大的存储空间[2-4]。最小二乘法以最小化误差的平方和为目标使所有数据点最为接近,曲线拟合效果良好[5]。但是LS以计算所有数据点为参考值,易受到离群点的影响[6-7]。不同算法各有缺陷,难以同时保证高效率和高准确度的应用需求,因此对主流圆拟合算法进行改进已成为该领域的热门研究方向。
在圆拟合算法研究中,研究人员将目光投入到提升Hough变换算法性能方面。文献[8]提出一种改进的Hough变换算法,通过最小误差原则对圆轮廓点随机抽样,运用聚类算法去除虚假圆心,最后通过圆心度的方法评价算法结果。文献[9]改进了Hough圆拟合算法,先通过圆的几何特性确定圆心和半径,同时通过聚类分析,组合较相似的候选圆,有效提升了计算速度并解决了多个假圆问题。最小二乘法拟合圆的方式也得到了一定修正。文献[10]提出了一种基于最小二乘法的圆拟合方法,其以几何距离差值平方和最小作为评价标准并结合迭代法,在非均匀采集离散点的情形下能有效提升圆拟合的精度。
以上研究分析某种圆拟合算法的缺陷并进行针对性地改进,未充分考虑融合不同算法的优势互补,且验证实验的角度和分析指标不够全面。本文提出了一种基于多级优化的圆拟合算法。该算法综合运用3σ准则、改进的随机抽样一致性(Random Sample Consensus,RANSAC)以及迭代加权最小二乘法,依次实现了粗大误差点剔除、高质量内群点提取和精细化处理。其中对RANSAC算法作出3处修整,对迭代加权最小二乘法设置了迭代终止条件。与以往研究不同,本文算法对不同程度的噪声进行分步分层处理,更具有针对性,使得优化效率和准确率明显提升。同时本文算法从缺损、杂质干扰和椒盐噪声3个角度全面验证了算法性能,并评价了算法的稳定性等数学指标。
1 算法介绍
本文算法包含粗大误差点剔除、高质量内群点提取和精细化处理3个阶段,分别采用3σ准则、改进的随机抽样一致性以及迭代加权最小二乘法逐层优化。
1.1 3σ准则
偏离圆心较大的离群点难以满足正态分布,且对于圆心坐标的准确提取影响较大。假设所有轮廓点满足正态分布,本文算法可运用3σ准则处理误差较大的离群点[11]。
3σ准则又名经验法则,被用于快速推算满足正态分布且已知平均数和标准差的数据。其定义为:数值落在区间(μ-3σ,μ+3σ)中的概率是99.74%,μ表示数据的均值。数值x分布在区间(μ-3σ,μ+3σ)以外的概率低于0.30%,通常认为该事件在实际问题中不会发生。如果一组数据满足正态分布,那么该组数据中和平均值的偏差大于3倍标准差的值为异常值,且该类值发生的概率较小。
1.2 改进的随机抽样一致性
本文算法已用3σ准则完成对误差较大的离群点,下一步运用改进的RANSAC随机抽样选出最多的内群点以及对应圆拟合模型。
随机抽样一致性是一种可以用来平滑携带大量干扰点的实验数据,并且能运用实验数据拟合模型的方法[12-13]。随机抽样一致性通过反复抽取数据中的一组随机子集来得到最佳结果[14]。其算法流程可归纳为以下步骤:
步骤1首先从数据点集M中随机抽选m个数据点,恰好能够组成一个最小的子集,根据该子集构建模型参数;
步骤2遍历数据点集M中的所有数据点,依次判断它们是否满足上一步所确定的模型(在假设的距离阈值t内)[15],得到满足条件的点群集合Si(一致集);
步骤3计算Si的大小(例如内点的数目)是否大于假定的某个阈值T,如果大于T就对其中所有点重新估计模型并结束;反之重新选择新小子集m,并重复上述过程;
步骤4经过数次实验后,便可以选出最大的一致集Si,最后用Si中的所有点重新估计模型参数。
传统的RANSAC圆拟合算法仍有一定缺陷,本文的改进方式为:
改进1降低子集抽选的随机性。在步骤1中,通常设定m=3作为最小子集,利用3个不共线的点拟合出圆模型。然而选择的最小子集随机性太强,不一定可拟合出圆模型即出现多点共线或者重选现象,由此带入圆模型计算会造成时间浪费。为此,本文对随机选择的3点进行共线/重选判定,挑选出不共线的点集再进行下一步的圆模型计算,以降低子集抽选的随机性。具体判定方法为通过判断斜率是否相等排除3点共线的情况,通过判断坐标是否相等排除3点中有重复选择的情况。
改进2圆模型的降次运算。在步骤1中,采用如下所示的圆模型计算式
x2+y2+Dx+Ey+F=0
(1)
将3点设为(x1,y1)、(x2,y2)、(x3,y3),分别代入式(1)并联立求得D、E、F,则圆心坐标为(-D/2,-E/2)。该方法带有平方运算,耗时较大。本文算法利用圆上弦的中垂线定理(两条不平行的弦,其垂直平分线的交点交于圆心)替换上述模型计算方法,将二次运算转化为一次运算,从而降低高次计算带来的时间消耗。圆上弦的中垂线定理原理如图1所示,联立任意两点求得直线方程l1和l2分比为y=k1x+b1,y=k2x+b2,则弦的垂直平分线方程为y=-(1/k1)x+m1,y=-(1/k2)x+m2,两式的交点即为圆模型的圆心坐标。

图1 圆上弦的中垂线定理原理Figure 1. Schematic of the center perpendicular line theorem of the chord of a circle
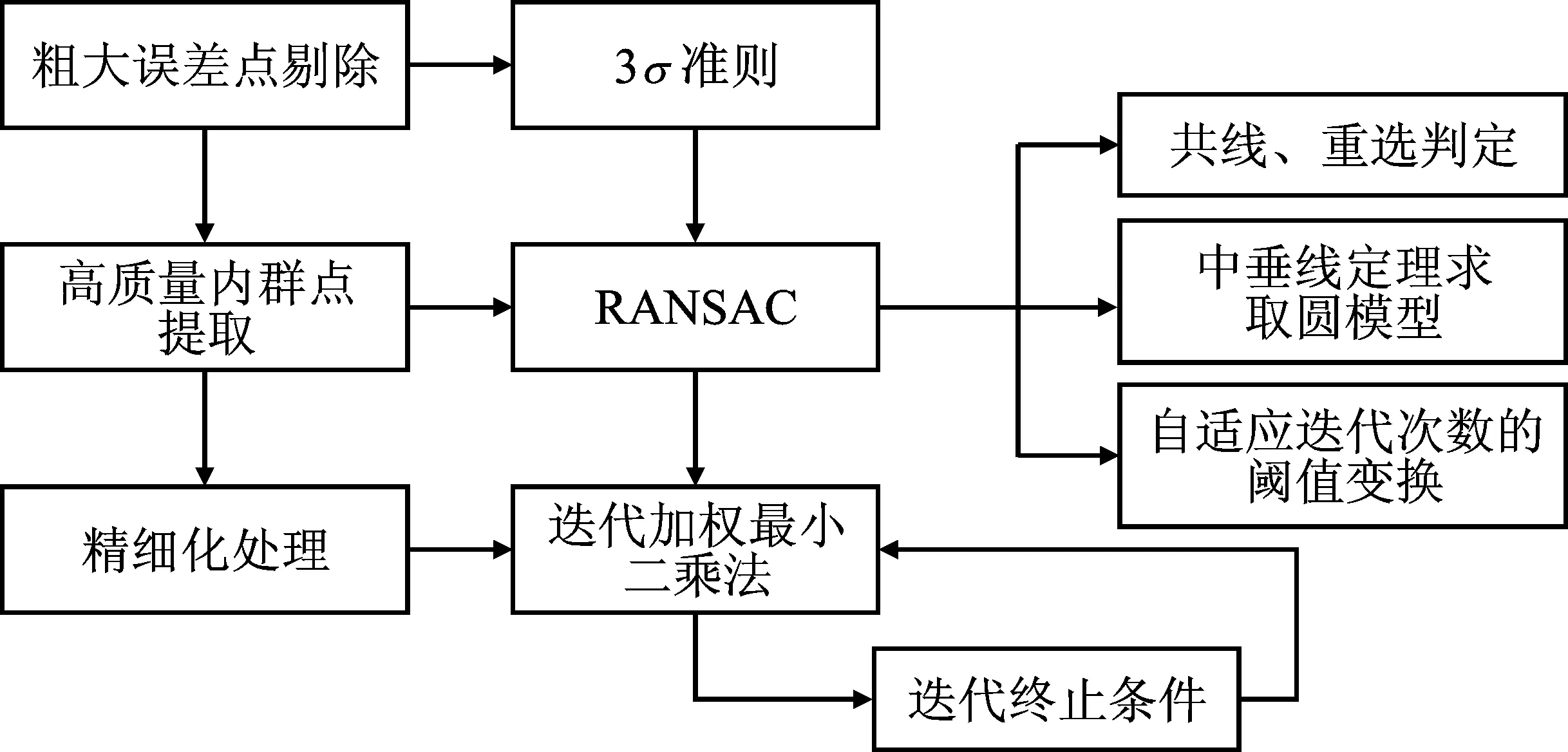
图2 算法流程Figure 2. Flow of the proposed algorithm
改进3自适应迭代次数的阈值变换。在步骤3中,通常设定足够多局内点数目(阈值T)为条件进行随机搜寻。由于实际中圆轮廓点数不可知,阈值T的设定通常带有主观性和经验化,导致鲁棒性较差[16-17]。为此,本文算法引入置信度P进行循环中断,每次迭代时根据类内点比例自适应更新迭代次数,当满足置信度要求时即可跳出循环,从而实现不同情况的普适性,保证算法结果的可靠性。在循环过程中,应至少有一次采样使得采样出的m个点均为类内点,才能保证在循环的过程中至少有一次采样能取得目标函数的最大值。其中置信度一般设置为[0.95,0.99]。改进后的迭代次数K变为
(2)
式中,P为置信度;K为迭代次数;m为子集大小;ε为类内点在点集中所占的比例。
1.3 设置迭代终止条件的迭代加权最小二乘法
随机抽样一致性基于估计模型得到相对最优解,有必要对其再进行精细化处理。本文算法对上一步所得点群再进行迭代加权最小二乘法处理。
最小二乘法拟合圆容易受到离群点的影响,产生偏离真实值的结果。由此出现了迭代重加权最小二乘法(Iterative Reweighed Least Squares,IRLS),其能够在一定程度上处理以上问题[18]。IRLS加入了距离权重函数,可通过计算所求的距离分配距离的权重。
对圆拟合来说,引入权重ωi,对于离圆心较远的点,设置权重小于1,可以削弱对拟合圆的影响。本文采用Tukey距离权重函数,因为其引入了距离平方,收敛效果更好。Tukey权重函数的计算式如下所示。
(3)
基于IRLS方法拟合圆的原理如下所示:圆的标准方程式为
(x-a)2+(y-b)2=c2
(4)
建立最小化误差函数S
(5)
式中,A=-2a;B=-2b;C=a2+b2-c2。
引入距离权值ωi
(6)
基于式(6),对A、B、C分别求偏导
(7)
同理可得
(8)
(9)
将式(7)~式(9)变换为矩阵形式。
(10)
通过式(10)可以求解出A、B、C,从而求解出a、b、c。通常采用标准的最小二乘法拟合圆实现迭代的初始化,此时ωi=1。在后期迭代时,权重不断改变,逐渐剔除不同偏离程度的离群点。
传统的IRLS通常设置固定的迭代次数,导致容易发生欠收敛或者过收敛现象,进而造成结果不准确或者时间浪费。由于在迭代过程中,权重不断发生改变,当权重不再改变时,点群也固定不变,其结果趋于稳定,即达到收敛,所以本文可以将迭代的终止条件设置为当前迭代与前一次迭代圆心误差与半径误差小于10-2,此时得到的结果是基本收敛精确值。迭代的终止条件设置为
|Ck+1-Ck|<10-2
|Rk+1-Rk|<10-2
(11)
式中,C为圆心坐标;R为圆心半径。
1.4 算法描述
本文算法的设计原因与合理性描述为:3σ准则可剔除一组数据的粗大误差,降低了下一级RANSAC随机抽样的压力。RANSAC是基于估计值得到运算结果,其最终结果不够精确,迭代加权最小二乘法对权重进行不断修正,运算结果足够可靠,所以其可作为RANSAC算法的后处理操作。同时当噪声较大时,迭代加权最小二乘法拟合圆可能会失效,3σ准则和RANSAC作为先前处理可剔除大部分噪声,从而也维护了迭代加权最小二乘法的有效性。
本文算法的具体流程如下:
1)获取输入图片的轮廓,对所有轮廓点进行一次最小二乘圆拟合,得到粗圆心和粗半径。
2)计算轮廓所有点和粗圆心的距离及其与粗半径的差值d1,求其均值及标准差s。比较d1与3s的大小,若d1≤3s,该点留下,否则剔除。
3)从上一步得到的点群随机抽取3点,排除共线、重选现象,筛选出符合条件的合理点。
4)利用圆上弦的中垂线定理得到圆的半径r和圆心坐标,计算轮廓点与r的距离d2,若|d2-r|≤t(设置阈值t=kr),则该点为内群点。统计内群点的数量,进入下一次的迭代。
5)依次迭代,加入循环中断,设置迭代次数K=log(1-P)/log(1-εm)。当达到所设置的参数条件时迭代结束。
6)对所得到的内群点用迭代加权最小二乘法进行精细化处理,设置γ=2median(δi)/0.675并不断迭代,迭代的终止条件为|Ck+1-Ck|<10-2和|Rk+1-Rk|<10-2。
2 算法介绍
在实际工况中,影响圆拟合的准确度因素主要有缺损圆、杂质干扰以及其他噪声。如图3所示,现绘制一个圆心坐标确定为(328.0,242.5)的圆,分辨率为640×480,在Vistual studio软件中基于C++语言编程,对其添加不同干扰噪声。针对上述3种情景。对本文算法进行探究,实验流程为:原图 →灰度化→Canny提取边缘→算法拟合。

图3 实验测试圆绘制Figure 3. Experimental test circle drawing
2.1 缺损圆
在不同缺损程度下,本文算法的拟合效果以及与其他算法的对比如图4所示。其中,LS表示最小二乘法,IRLS表示迭代加权最小二乘法,Hough表示OpenCV中的霍夫变换圆检测。

(a)
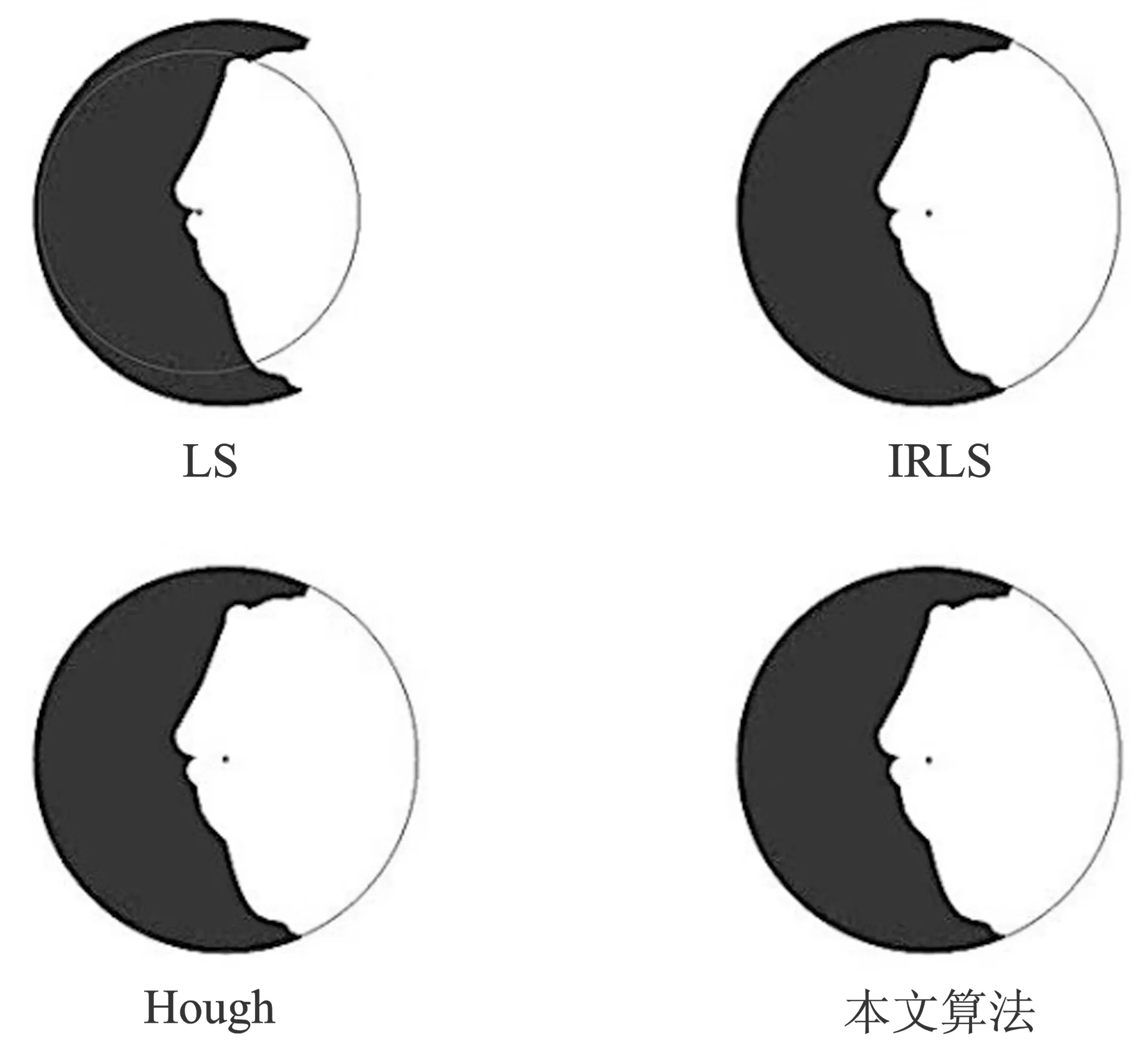
(b)图4 缺损圆下不同算法的拟合效果(a)缺损圆1 (b)缺损圆2Figure 4. Fitting effect of different algorithms under defect circles(a) Defect circle 1 (b) Defect circle 2
从图4和表1可以看出,随着圆缺损的程度不断增大,LS对缺损噪声表现较为敏感,虽然运行时间最短,但拟合效果与真实值偏差过大。IRLS对最小二乘法进行了改进,降低了对缺损噪声的敏感度,但当缺损较大时,其拟合偏差不断增大,且拟合偏差超过了1 pixel,所以IRLS对缺损较大的圆拟合效果仍有待改进。基于OpenCV的Hough变换运用了梯度法,有效降低了原始算法的执行时间,但同时也使得原始Hough的检测准确性效果有所降低,最大偏差为1.5 pixel。本文算法运行时间较短,短于IRLS和Hough变换,所举工况的最大偏差在0.7 pixel以内,拟合准确性优于其他3种算法,验证了本文算法在缺损圆下的有效性。本文算法性能更优是因为随着圆缺损的程度不断增大,3σ准则仍能剔除掉误差较大的缺损点,改进的随机抽样一致性抽样压力降低,仍能估计出较优模型,而IRLS的权重分配函数使得缺损点对拟合圆心的影响逐渐降低,迭代终止条件保证了较优的准确率。

表1 缺损圆下不同算法的拟合数据Table 1. Fitting data of different algorithms under defect circles
2.2 杂质干扰
在不同杂质程度下,本文算法的拟合效果以及与其他算法的对比如图5和表2所示。
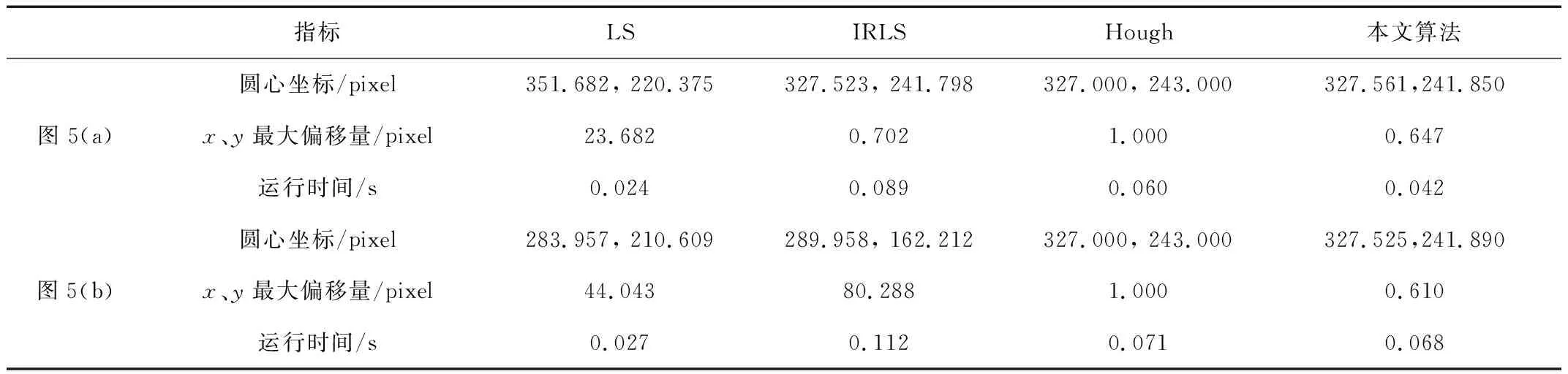
表2 杂质干扰下不同算法的拟合数据Table 2. Fitting data of different algorithms under impurity interference

(a)
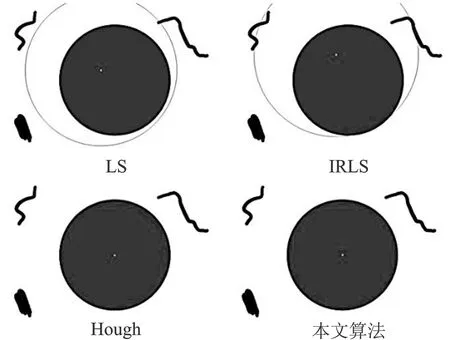
(b)图5 杂质干扰下不同算法的拟合效果(a)杂质干扰1 (b)杂质干扰2Figure 5. Fitting effect of different algorithms under impurity interference(a) Impurity interference 1 (b) Impurity interference 2
从图5和表2可知,随着圆的杂质干扰程度不断增大,LS对杂质干扰较为敏感,虽然运行时间最短,但拟合效果与真实值偏差过大,这是因为更多的干扰点加入了LS的参考基准点集,使得算法本身对杂质干扰点的信任度增加。当干扰程度较低时,IRLS可以保持较好的拟合效果,但当干扰程度较高时,其拟合偏差过大,且运行时间过长。基于OpenCV的Hough变换拟合的最大偏差为1 pixel,拟合准确度仍不够精确。本文算法在运行时间上和拟合准确度上表现较好,两种指标均优于IRLS和Hough变换。所举工况的最大偏差小于0.7 pixel,拟合准确度好于LS,验证了本文算法在圆杂质干扰下的有效性。本文所提算法性能更优是因为随着圆受到的杂质干扰点不断增多,3σ准则仍能剔除掉误差较大的干扰点,同时使得下一步改进的RANSAC抽样的时间成本降低,IRLS的权重分配函数使得杂质干扰点对拟合圆心的影响逐渐削弱,迭代终止条件可得到较好的拟合效果。
2.3 其他噪声
椒盐噪声是图像处理中比较常见的一种噪声,表现为白色或者黑色。本文实验以椒盐噪声为例,为方便显示拟合效果,制作3通道的圆轮廓图像作为原始图片,如图6所示,其分辨率和圆心坐标与图3相同。实验流程为:原图→二值化(单通道)→算法拟合。因噪声常在原图(3通道)中产生,算法拟合习惯在单通道中处理。故在原图添加椒盐噪声并统计二值化(单通道)噪声比例(约20%~265%)。检测到单通道图中圆轮廓初始像素个数为4 759,算法运行10次,取平均值得到的拟合数据如表3所示。
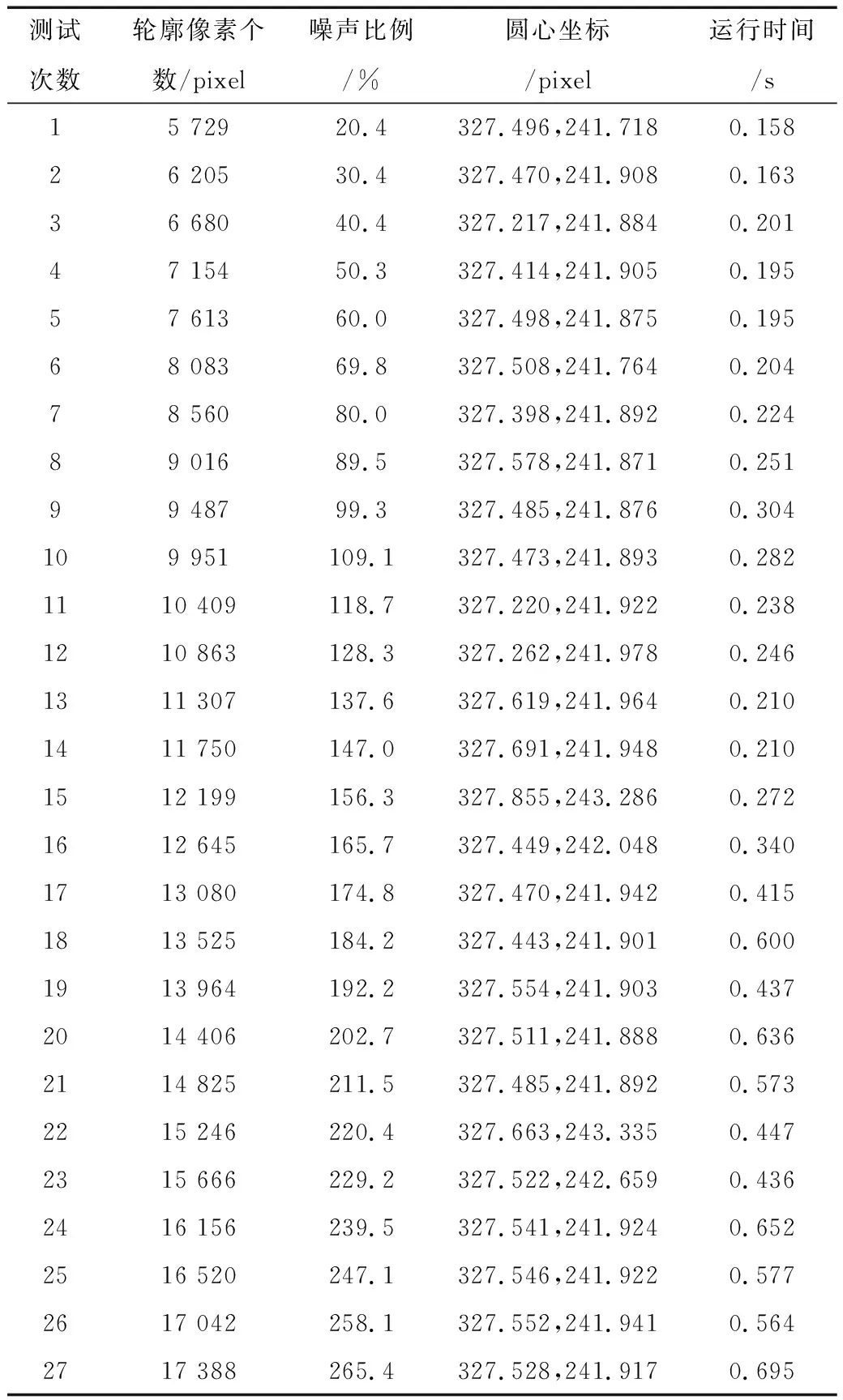
表3 不同噪声比例下本文算法的拟合数据表Table 3. Fitting data of the proposed algorithm under different noise ratio
在表3中14组噪声比例下,x、y最大偏差及算法的运行时间的走势分别如图7(a)和图7(b)所示,最大偏差的性能指标如表4所示,算法在原图中的拟合效果如图8所示。
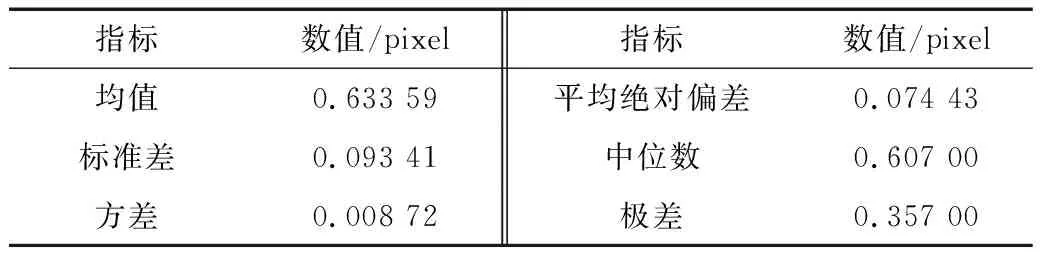
表4 最大偏差的性能指标表Table 4. Performance index of maximum deviation
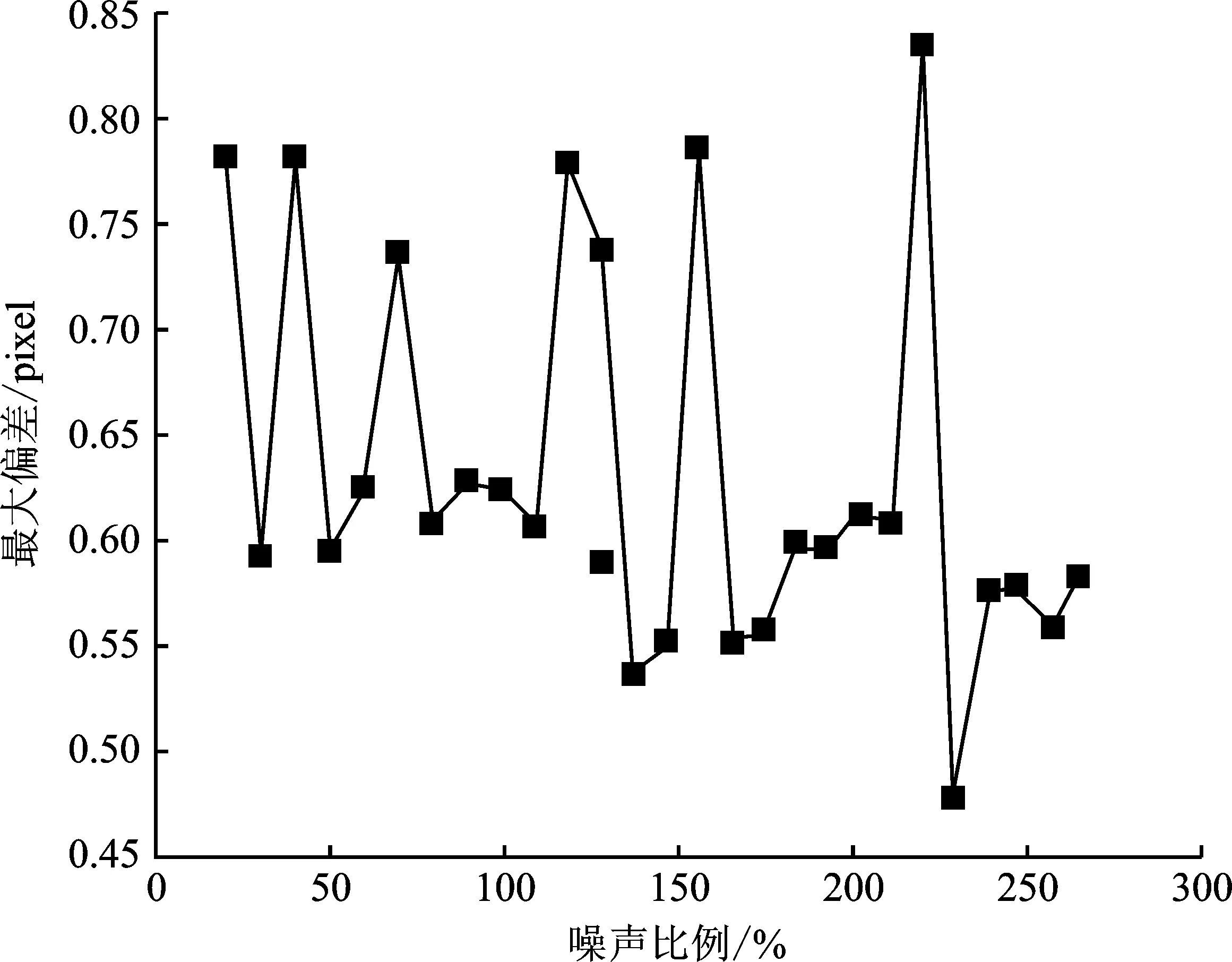
(a)

(b)图7 不同噪声比例下x、y最大偏差及算法运行时间的变换趋势(a)最大偏差结果 (b)运行时间结果Figure 7. Variation trend of x,y maximum deviation and algorithm running time under different noise ratio(a)Result of maximum deviation (b)Result of running time

(a)

(b)图8 不同噪声比例下本文算法的拟合效果(a)噪声比例80.0% (b)噪声比例265.4%Figure 8. The fitting effect of the proposed algorithm under different noise ratio(a)Noise ratio of 80.0% (b)Noise ratio of 265.4%
从图7可以看出,在拟合准确度方面,随着噪声比重的增加,拟合的最大偏差仍保持在1 pixel以内,说明在大量噪声的干扰下本文算法仍维持较高准确率。在运行时间方面,随着噪声的增多,算法在噪声不低于150%左右时,运行时间有波动上升的趋势,最长约0.3 s;在约高于150%且不低于265%时,运行时间虽有显著增长,但整体未超过0.7 s,能够满足日常的实时性需求。
从表4可以看出,拟合过程中最大偏差的均值和中位数相近,在0.6 pixel左右,拟合准确度较高。结合图7(a)来看,拟合的最大偏差在均值附近虽有一定波动,但总体来看其方差为0.008 72,标准差为0.093 41,数值较小,表明算法具有较强的稳定性。
综上可以得出结论,噪声的增多虽使本文算法的时间负累有了少量的增加,但并未对拟合准确率和稳定性产生较大影响,在其他噪声干扰下本文算法的有效性得到验证。这是因为3σ准则、改进的随机抽样一致性以及IRLS均具有去噪能力且逐渐降低,但前面两者的去噪能力使得层级间的递进传递关系未受到较大影响,传递的噪声未使分级准则达到失效阈值,从而保证了拟合的准确度和稳定性。然而当噪声不断增多时,分布在各个层级的噪声也在增加,使得算法整体的执行时间不断增大,这一规律在噪声较多时表现地更为明显。
由图8可知,本文算法在大量噪声干扰下,真实圆轮廓与拟合圆轮廓边缘大量重合,真实圆心与拟合圆心基本完全覆盖,拟合效果较为准确。与图7(a)相比,图7(b)噪声已达到其3倍之多,但从效果上看,二者拟合准确度并未有明显差别。
3 结束语
本文提出了一种新的基于多级优化的圆拟合算法。该算法综合运用3σ准则、改进的随机抽样一致性以及迭代加权最小二乘法依次实现粗大误差点剔除、高质量内群点提取和精细化处理,从而达到多级优化的目的。从缺损圆、杂质干扰和椒盐噪声3个方面进行实验验证,并与其他常见算法进行对比,最终验证本文算法具有较强的抗残缺能力和抗干扰能力,拟合效果优于其他算法。本文算法能抵抗大量噪声干扰,在噪声比例不超过265.4%的情况下,拟合精度小于1 pixel,运行时间不大于0.7 s,保持了高准确率和强稳定性,运行效率较高,能满足多数实时性需求。本文算法仍有一定的局限性,例如当噪声的干扰较大时,算法的执行时间仍需要进一步改进。未来可以考虑改进分步准则提升效率以进行拓展性研究。

