基于时空聚类的多源异构时序数据集成方法

陈 超，胡才亮，崔 钰，谢 芳，杨慧芳，王 健

（安徽明生恒卓科技有限公司，安徽合肥 230000）

数据集成是统计学的一个分支，现阶段相关领域学者对于数据集成的研究已经取得了一定进展，使得数据集成技术逐渐完善，然而，数据时空分布不均与数据混乱情况下的数据集成效果依然较差。尤其是工业信息、通信信息等各行各业所产生的庞大信息量通常都较为混乱，数据呈现无序性和多源性，因此，对多源异构的数据集成便成为了该领域的研究重点之一。

针对此问题，一些学者进行了相关研究。文献[1]提出了分布式数据集成方法，建立一种分布式环境下高性能数据工具，通过大数流式计算框架实现多源异构数据的集成，但该方式太过依赖于数据工具，不适用于普及使用。文献[2]提出了基于多目标优化技术的多源异构数据集成方法，通过建立多目标群交叉优化算法处理不平衡数据集，过滤大部分多源异构数据，以此完成数据集成，但该方式过滤掉太多数据，已无法满足统计学中对多源异构数据的集成要求。

多源异构的数据集成通常以时间序列形式呈现，数据量较大且集成难度增加，而利用传统方法进行多源异构时序数据集成出现执行和抽取时间较长、筛选准确率较低的问题，因此该文提出了基于时空聚类的多源异构时序数据集成方法。

1 多源异构时序数据协同处理

在进行数据集成时，需要将时序不同步的混乱数据进行同步处理，该文通过三种方式汇集时序数据，分别为滤除、插值以及混合式时序数据[3-4]。多源异构时序数据汇集过程如图1 所示。

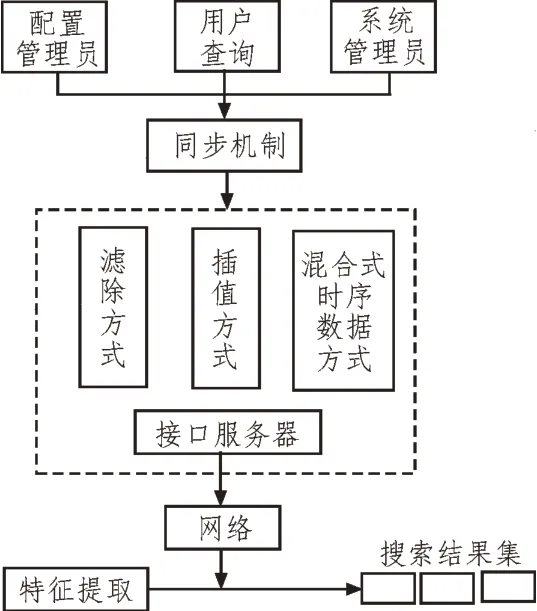
图1 数据汇集过程

在滤除处理过程中，选取最大的监测数据间隔作为时序，如果时序数据出现遗漏，则选取离时间节点最近的时序数据来代替[5-6]。与滤除处理方式相反，插值过程中采用最小监测数据作为时序数据，通过采集最近点的多源异构时序数据的平均值来填补缺失数据[7]。

混合时序数据汇集时间根据信息集汇聚的内容而定，通常把信息集中的时序数据之一视为新的时间或重定义新的时序。各个时序数据之间以新的汇集顺序为依据，生成监测时序数据[8-9]。

完成数据汇集后对多源异构时序数据进行协同处理。在对时序数据源进行整理后，针对时序数据的字段增加三个基础特性，包括时序数据标志、起始日期、时间间隔。同步处理后根据同步机制将时序数据录入虚拟数据库[10-11]。

通过分析数据汇聚层协调程度进行时序数据同步，时序数据的同步对于数据汇聚的协同程度影响很大，当汇聚的数据都是时序数据时，时序数据同步机制便开始运行，从数据汇聚层开始收集时序数据中的所有时序数据，如时序数据的名字、日期、大小、采样间隔、时序数据的去向等及其同步方法，以此实现数据同步[12-13]。

2 多源异构时序数据集成

实现多源异构时序数据协同处理后对数据进行集成，集成流程如图2 所示。

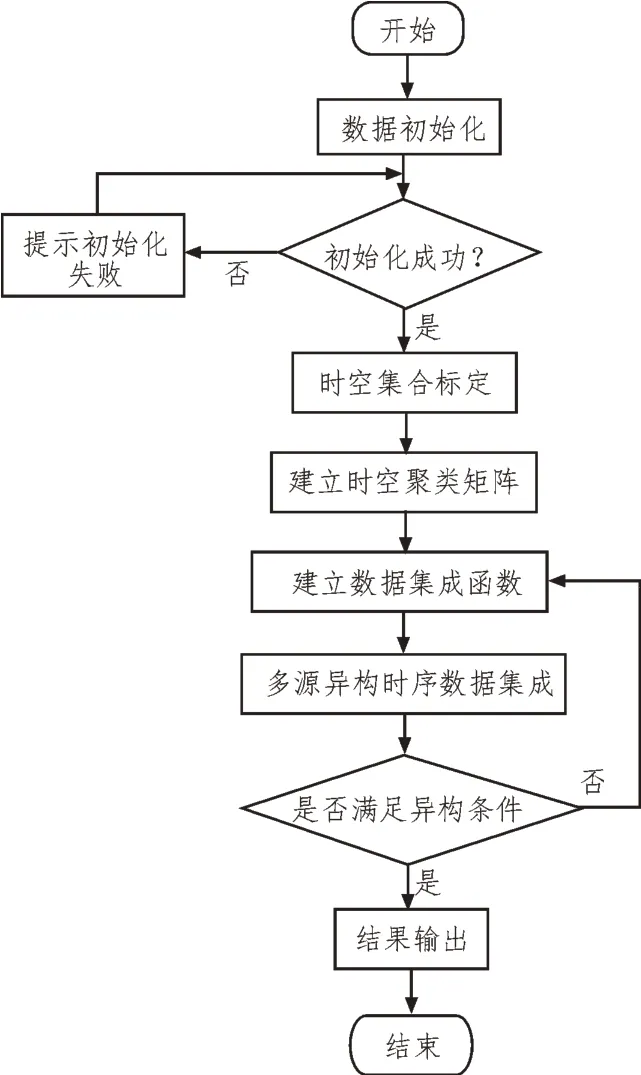
图2 基于时空聚类的多源异构时序数据集成流程

根据图2 可知，多源异构时序数据集成主要通过时空集合标定、建立时空聚类矩阵、建立数据集成函数、多源异构时序数据集成来实现。

2.1 时空集合标定

时空聚类以时空数据库为基础，时空数据库具备存储大量信息的能力，能够更好地对多源异构时序数据进行整合与分析，在执行数据储存指令时，时空集合可提取现有多源异构时序数据的处理条件信息，以此为基础，完善多源异构时序数据[14-15]。时空集合P计算公式如式（1）所示：

式中，Wn表示多源异构时序数据向量最小值；Wm表示最大多源异构时序数据向量最大值。

2.2 时空聚类矩阵

在时空集合标定结果已知的情况下，建立时空聚类矩阵，在时空聚类矩阵中，多源异构时序数据分为横向与纵向两种形式。在针对横向多源异构时序数据进行判定过程中，采用时空聚类算法中的最近邻分析算法，其表达式为：

式中，R表示最近邻分析结果；dobs表示在观测过程中节点与最近邻点之间的平均距离；dexp表示不同状态下的节点期望值。

由于最近邻算法只考虑到横向数据中的点对点情况，因此，对纵向多源异构时序数据进行分析时，需要引入时空聚类算法中的莫兰指数E(·)，通过计算莫兰指数的期望值I实现对纵向多源异构时序的判定：

式中，n为纵向排列数量。时空聚类矩阵可作为精准的信息判别条件，通过时空聚类矩阵描述时空数据库中的存储能力，当时空数据库的数据量达到目标值时，即可认为时空聚类矩阵进入饱和状态。

2.3 数据集成函数

数据集成函数是以时空聚类矩阵为基础建立的多源异构时序数据查询限定条件，由于时空聚类算法的应用性很强，随着数据信息量的增加，集成函数的极限值覆盖面积也会不断增加，直到能够满足多源异构时序数据的传输需求。数据集成函数D可表示为：

式中，Xn代表多源异构时序数据最小参量，Xm代表多源异构时序数据最大参量，且将信息参量混乱状态的传输情况考虑在内，Xn与Xm的差值越大，数据集成函数性能越优。

2.4 多源异构时序数据集成

多源异构时序数据集成就是利用时空聚类算法转换所有数据，数据集成主要分为两个过程，分别是数据分离与数据集成。通过数据集成的层次结构来选择集成的方式[16]。将每一条多源异构时序数据信息看作一个类，根据时空聚类算法规则集成越来越大的类，直到满足预设条件。通过时空聚类算法中的统计量G来判断多源异构时序数据期望，表达式为：

式中，E(G)为G统计量的期望值；wi为多源异构时序数据权重。

根据相似度的测量对时序聚类结果进行分组，比较数据库中的时间序列相似度，在同一个簇中相似度高的数据列为一组而不同簇中的信息数据相差较大。多源异构时序的集成是为了在不同时间域的同一个属性时间序列数据库中挖掘数据信息。无论是数据分离还是数据集成，用户都可以根据自己的要求来设计多源异构时序数据的分离和集成要求，从而更好地实现多源异构时序数据集成。

3 实验研究

为了研究该文提出的基于时空聚类的多源异构时序数据集成方法的实际应用效果，设计了相关实验。选用传统的基于多目标优化的多源异构数据集成方法和基于数据挖掘的多源异构时序数据集成方法与该文的集成方法进行对比。实验环境如图3 所示。

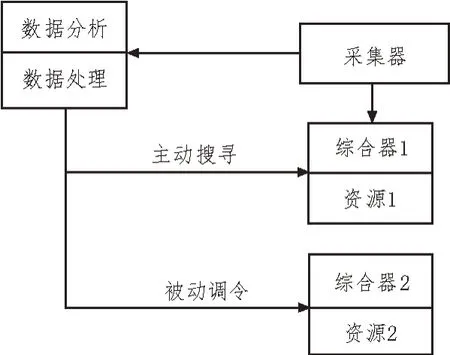
图3 实验环境

系统接口与数据库顺利连接后就会读取存储空间内的数据，采用自动抽取方式提炼图层要素，在后台完成数据执行和抽取，抽取过程不会显示详细的图形数据，抽取结果会直接输入到数据库内部。三种方法的数据执行时间和筛选时间实验结果分别如表1 和表2 所示。

表1 执行时间实验结果

根据表1 与表2 可知，该文提出的基于时空聚类的多源异构时序数据集成方法所用的数据执行和抽取时间都低于传统方法。由于用户具有多样性要求，因此需要抽取不同数据，该文提出的集成方法在数据抽取过程中，只针对数据库的部分数据进行提取，通过抽查分析解决这一问题，这样既能很好地存储相关数据，又能提高执行和抽取速度。

系统接口与数据库顺利连接后，需要重新获取数据库内部的空间数据，通过定义分析进行数据筛选，筛选准确率实验结果如图4 所示。

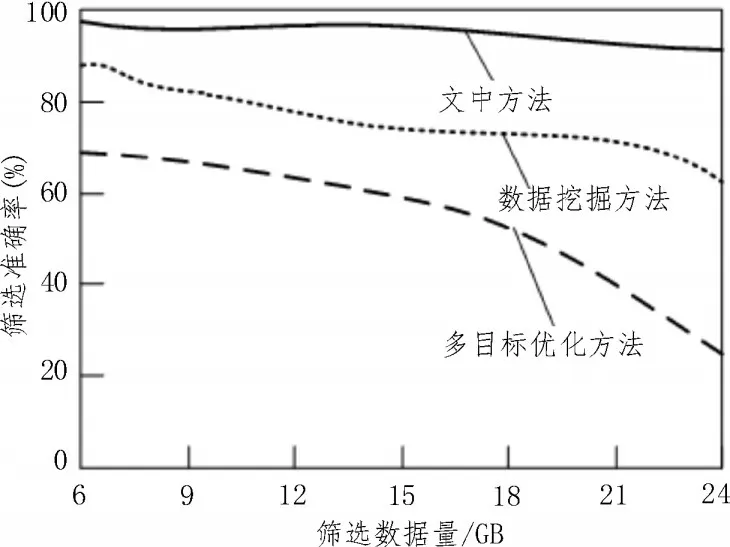
图4 筛选准确率实验结果

分析图4 可知，随着数据量的增加，筛选结果准确率开始呈现下降趋势，但是该文提出的集成方法的准确率始终保持较高水平，原因是该文的集成方法在筛选过程中会将数据转为shapefile 格式，采用时空聚类算法包含的时空数据库存放多源异构数据，并对其进行数据集成处理，通过数据命名确保筛选结果的正确性，而传统方法多采用盲目筛选的方式，筛选结果难以达到用户要求。

顺利完成筛选后对数据进行集成，实验结果如图5 所示。

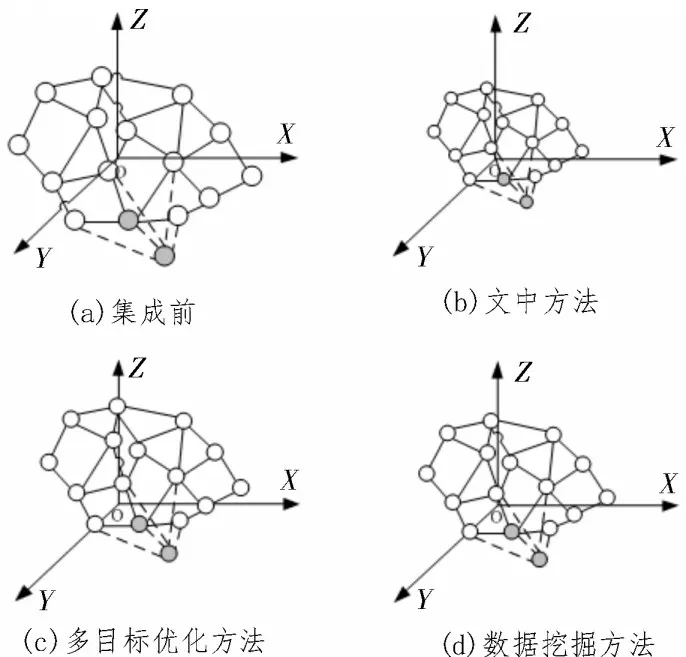
图5 数据集成实验结果

观察图5 可知，该文提出的集成方法的集成效果更加好，原因是该文方法在对数据进行处理时，能够很好地实现空间坐标转换，提高了集成效率，确保集成效果更好，而传统方法在集成过程中容易受到外界因素的影响，集成效果相对较差。

4 结束语

数据集成是解决大量数据信息存储与分析的方法之一，对于多源异构时序数据信息的集成需要加入具有针对性的算法来实现。该文通过时空聚类算法建立时空聚类矩阵，从而完成多源异构时序数据的集成。实验表明，所提出的基于时空聚类的多源异构时序数据集成解决了传统方式存在的不足，以此保障多源异构时序数据集成的速度与质量。