基于负荷分解与聚类融合的短期用电负荷预测研究

马晓琴，马占海，罗红郊，张华铭

（1.国网青海省电力公司信息通信公司，青海西宁 810000；2.北京清软创新科技股份有限公司，北京 100085）

短期负荷预测通常指预测最近几个小时内到不超过一周的负荷情况，并根据该情况调节近期的发电量，从而使电力能源的生产更加高效，同时还可以辅助电力公司采用动态定价的方案，以促进用户合理用电[1-3]。由于负荷的不确定性以及电网供电的复杂程度不同，负荷预测仍需更合理的算法来提高其精确性[4-5]。随着智能终端的广泛应用，基于智能算法的负荷预测也成为了研究热点，例如自回归综合移动平均模型（Autoregressive Integrated Moving Average Model，ARIMA）[6]、多线性高斯过程回归（Gaussian Process Regression，GPR）等[7-8]。而在机器学习（Machine Learning，ML）领域也有诸多方法可适用于短期负荷预测，例如支持向量回归（Support Vector Regression，SVR）、人工神经网络（Artificial Neural Network，ANN）及深度神经网络（Deep Neural Networks，DNN）等[9-11]。

智能电力仪表与通信系统可提供负载的详细信息，然而其在配电系统中的应用仍处于起步阶段。早期发表的关于负载分析的研究工作囊括了不同类型的聚类，包括K-均值（K-means Clustering Algorithm，K-means）、模糊聚类（Fuzzy C-means Algorithm，FCM）等。但大多数可用的基于机器学习的负荷预测方法，通常仅依赖单一数据源的历史记录，属于单任务学习方法的范畴。因此在分析负荷动态的随机特性时，上述方法均难以准确预测。该文探讨了基于负荷特征的多数据源负荷分解与聚类融合方法，并基于贝叶斯时空高斯过程（Gaussian Process，GP）模型提出了短期用电负荷预测算法。此外还通过对公开数据集进行预测研究，证明了所提算法的优越性。

1 负荷分解

大多数配电设施没有关于其负荷组成的准确信息，而这些信息对于充分且经济地规划电力网络则较为关键。该文针对这一问题采用惩罚最小二乘回归（Penalized least-squares Regression）和欧氏距离法（Euclidean Distance）来量化馈线负载的构成，以准确识别未知负荷情况的类型。

1.1 数据准备

为了提供有意义的数据分析，需要将负荷配置转换为可比较的形式。因此，可将每半小时的功耗转换为单位化的测量值。根据负荷特征，首先将五天工作日平均化为一天，而将周六和周日表示为一个单一的时间段，得到一周的负荷单馈电曲线，如图1 所示。

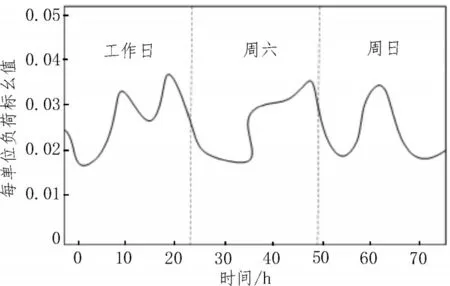
图1 单馈电线负荷曲线

然后将每个已知的负荷分配到正确的扇区，再通过使用不同负荷曲线间欧氏距离开发的程序分析数据并进行检查。欧氏距离由毕达哥拉斯公式推导而来，根据精度假设每个负荷图外形有144 个数据点，则其计算公式如下：

式中，a和b是计算负荷图外形之间距离的参数。该文采用欧氏距离法来检查分类假设，由于错误的分类可能会在错误的特征点形成聚类，所以该方法有助于聚类算法的实现。且当分解未知的负载分布时，其将显著改进结果的准确度。

1.2 分解方法

此外，欧氏距离法还可用于分析已知及未知的曲线轮廓。假设每个负荷曲线间的大部分差异是由具有其他部门影响因素的曲线来解释的，则基于这种假设是原因是电力线或变压器可能永远不会只向一个部门供电。通过比较每个负荷配置间的距离可重新分配一个新的部门细分比例，进而确保负荷配置的正确分配。

欧氏距离过程首先为每个负荷数据创建一个距离矩阵，并对每个距离进行4 次方缩放，具体如式（2）所示，从而使较近的轮廓具有更大的影响：

创建一个距离矩阵D，具体如式（3）所示：

式中，n是已知轮廓的数量，文中取值59。

为了重新分配每个轮廓的比例，将缩放距离倒置，并将每个轮廓的值之和线性缩放回1，如式（4）所示。由此，将迫使较小的距离比其他距离具有更高的值。又因为轮廓的分解不应由同一轮廓组成，因此对角线可以设置为0。

计算这些k值的目的是将每行的总和缩放为1，k值的计算方法如下：

通过使用这些值，能够确保每个轮廓的新比例之和均等于1。

2 聚类融合

上述方法着眼于负荷轮廓区别的距离，且使用大数据集进行负荷分解。而聚类方法则注重为每个部门创建一组特征轮廓，并为创建这些特征轮廓配置文件应用了K 均值聚类算法[12-14]，同时还将相似的配置文件集分为一组。与其他聚类方法一致，K 均值使用欧氏距离来确定向量轮廓是否与其他类似。为了保证该种聚类方法能产生最准确的结果，需确定每个部门的最佳聚类数。轮廓显示特定簇中指定的轮廓与其他簇的距离，而利用月平均值可显示数据的聚集程度。然后通过比较不同聚类值范围内的平均值，即可确定最佳聚类数。

对应于最大的负荷平均轮廓值，以月为单位的每个特征属性均会聚集到各自的部门分类中。随后可将每个集群中的配置文件平均化，并作为每个子聚类的基础，用于分解未知的负荷特征。最终再通过最小化完成这一过程，具体计算方式如下：

式中，yi是实际未知轮廓，X是特定月份的特征轮廓矩阵，J2(f)是粗糙度的惩罚，λ是平滑参数。将该方程最小化以找到贡献向量的最佳拟合p，从而给出特定月份的随机馈线贡献。并在研究中的每个月重复此种最小化处理算法，且允许按月计算贡献量。

表1 给出了使用这种负荷聚类方法对公开数据集上某区域每个未知馈线的分解聚类情况。其可分为8 个部分，分别为A1、A2、B1、B2、C以 及D1-D3。该程序通过选择配置的最佳线性组合，来最小化聚类误差。

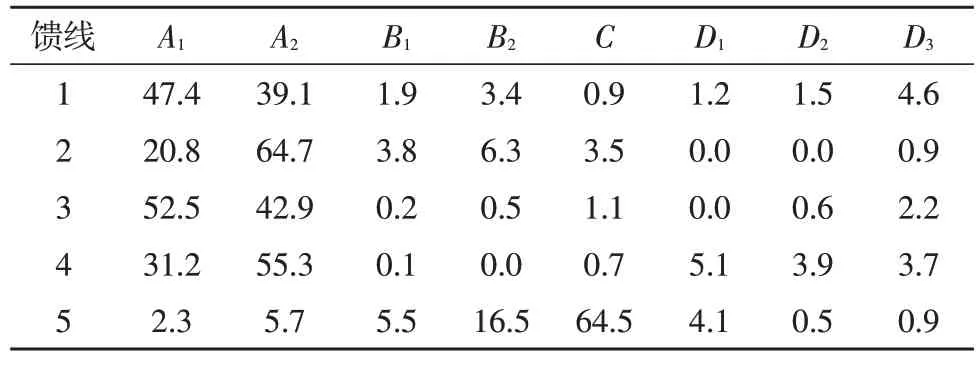
表1 负荷馈线分解各部分占比（%）

3 贝叶斯短期用电负荷预测算法

3.1 用电负荷空间依赖性

通过上述负荷分解以及聚类融合，可以将用电区域的负荷量（E）特征由下式分解表示：

式中，μ为用电量数据漂移均值，η为数据随机过程，e为负荷波动测量误差。式（7）反映了数据间的系统级相关性，并可用于提高预测精度。

短期用电负荷预测算法通过将μ、η及e相似或相关的行为分组到一个集群中，再根据用户的电力消费模式进行聚类，以量化获取各参量。需要注意的是，若在空间上的用户负荷呈现出一定的聚集规律，则η也会是有空间特征的随机过程。通常情况下，电网的配电拓扑布置与馈线的分支相连，距离较近的馈线负荷可能比相距较远的馈线负荷更为相似，这将导致用户负荷具有空间相关的可预测规律。

3.2 多区域贝叶斯高斯过程

随着电力智能检测设备实时性与精度的提升，负荷波动测量的误差e逐渐减小，故可忽略。因此，上述模型可简化为：

式（8）为贝叶斯时空高斯过程，其重点是获取特征值参量[15-16]。平均值μ通常被假定为与耗电量相关的变量线性模型，GP则指正态分布的高斯过程系数。

通过在众多预测任务进行的同时互相融合多个用电区域的负荷数据，能在一定程度上改进预测效果。假设有Z个用电区域，对于用电区域l，l=1,2,…,Z，通过上述负荷聚类融合后，获取的聚类类别包括N种。而拟建的多区域贝叶斯时空高斯过程模型具有以下模型结构：

式中，β是各相关变量的系数。同时，给出了每个区域的历史用电负荷数据集X以及区域间的初步相关信息。GPZ指第Z个区域正态分布的高斯过程系数，i=1,2,…,N。多区域贝叶斯时空高斯过程模型有两个预测目标，多区域预测的目标是评估β1,…,βZ的具体数值，而GP的目标则是每个用电负荷区域数据预测模型的参数估计。

3.3 多区域BSGP参数估计迭代算法

为了建立多区域贝叶斯时空高斯过程模型，应首先获取每个负荷区域的参数值。然后将结果联合，并按照区域之间的制衡关系衍生出综合参数值。其中μ的多区域预测评估系数βl应根据多区域数据联合估计，而GPl则是特定于用电区域的参数，可基于用电负荷区域l的编号分别估计获取。μl的估计精度会直接影响GPl的精度，反之GPl也会影响μl。该文提出了一种迭代融合算法，用于计算所有用电区域的参数，设计的短期用电负荷预测算法总体流程如图2 所示。

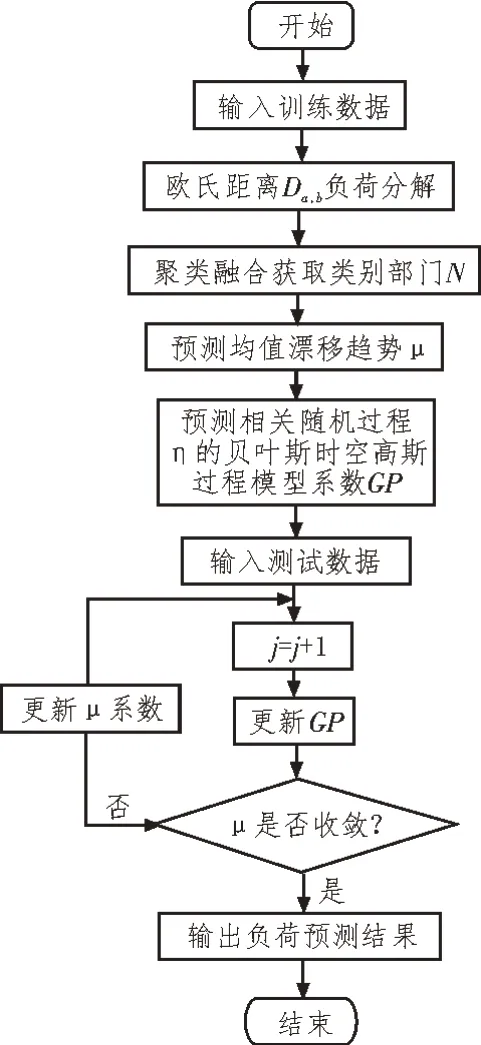
图2 短期用电负荷预测算法流程

输入训练数据后，在第j次迭代中，通过减去在j-1 次迭代中从电力消耗数据获得的高斯过程系数来更新μ的参数。然后预测相关随机过程的贝叶斯高斯模型系数GP，再输入测试数据进行收敛验证，进而根据μ的变化情况来判定收敛性能。若未达到收敛程度，则在下次迭代前，应减去第j次迭代时的μ值来更新GP系数。这一过程迭代循环进行，直至达到收敛标准后停止。最后将预测的用电量与实际负荷测量值进行比较，得出预测误差，从而评估预测算法的有效性[17]。

4 算法预测效果验证

为了验证基于负荷分解与聚类融合的短期负荷预测算法效果，在公开数据集上随机选择一周的负荷数据作为样本进行实验。在Matlab 平台上进行算法编程及数据处理，并将其与K-means 聚类负荷分析预测算法进行比较。图3 为使用该算法得到的短期用电负荷预测结果、实际负荷情况以及K-means算法负荷预测结果的对比图。

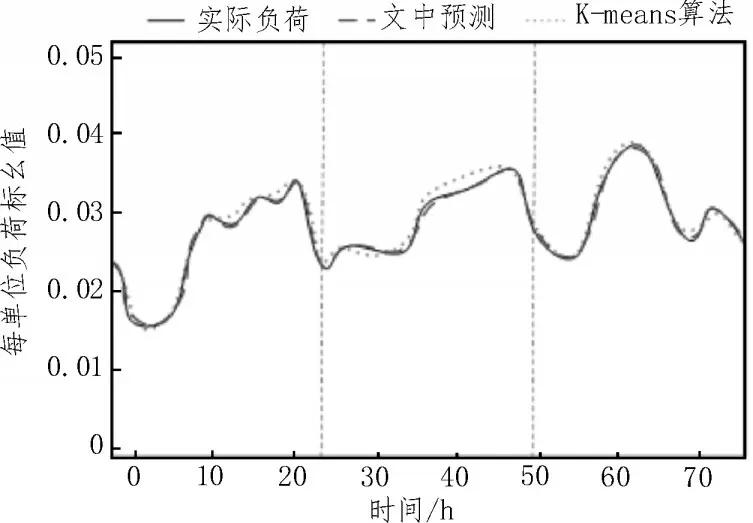
图3 预测负荷与实际负荷对比

从图中可看出，所提算法能够较好的预测实际用电负荷的走向。且与K-means 负荷预测算法相比，在负荷变化较快时的准确性更高。表2 则给出了两种负荷预测算法与实际测量负荷的误差对比。由表可知，该文所提算法的预测效果更优，尤其是在周末，K-means 负荷预测算法的误差较大，而该算法仍可保持较高的准确度。

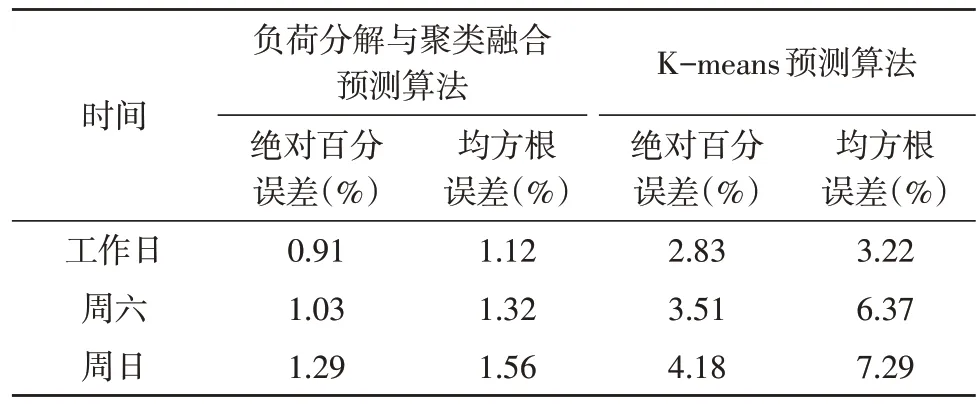
表2 预测误差结果对比

两种算法运行的消耗时间如图4 所示。从图中可看出，与K-means 算法相比，该文算法显著节约了运行时间。此外，随着预测区域的扩大，该算法仍能保持较快的运行速度及较高的预测精度。

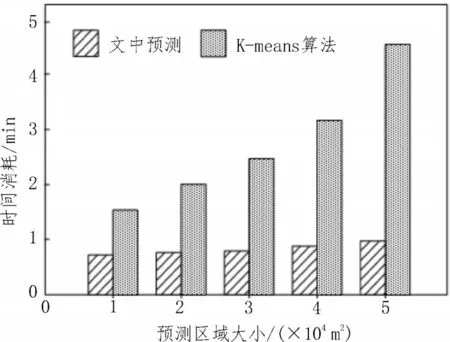
图4 不同算法运行消耗时间

5 结束语

文中通过采用贝叶斯时空高斯过程模型来描述不同用电区域之间的相关性，实现了对动态随机负荷的准确预测。同时，初始负荷分类需要具有一定的准确性才能实现正确的分解，该文使用欧氏距离来确定负荷曲线集之间的相关模式，保证了准确的负荷聚类。基于公开数据集的实验证实了算法具有较高的预测精度与较快的运行速度，该方法对于后期电网用电负荷的数字信息化管理预测具有重要意义。