An Optimal Control-Based Distributed Reinforcement Learning Framework for A Class of Non-Convex Objective Functionals of the Multi-Agent Network
Zhe Chen and Ning Li,,
Abstract—This paper studies a novel distributed optimization problem that aims to minimize the sum of the non-convex objective functionals of the multi-agent network under privacy protection, which means that the local objective of each agent is unknown to others.The above problem involves complexity simultaneously in the time and space aspects.Yet existing works about distributed optimization mainly consider privacy protection in the space aspect where the decision variable is a vector with finite dimensions.In contrast, when the time aspect is considered in this paper, the decision variable is a continuous function concerning time.Hence, the minimization of the overall functional belongs to the calculus of variations.Traditional works usually aim to seek the optimal decision function.Due to privacy protection and non-convexity, the Euler-Lagrange equation of the proposed problem is a complicated partial differential equation.Hence, we seek the optimal decision derivative function rather than the decision function.This manner can be regarded as seeking the control input for an optimal control problem, for which we propose a centralized reinforcement learning (RL) framework.In the space aspect, we further present a distributed reinforcement learning framework to deal with the impact of privacy protection.Finally, rigorous theoretical analysis and simulation validate the effectiveness of our framework.
I.INTRODUCTION
DISTRIBUTED optimization [1]–[4] has been widely applied to many scenarios such as smart grids [5], [6],traffic networks [7], [8], and sensor networks [9], [10].In these works, the whole task is accomplished by a group of agents with privacy protection, which means that the local objective function of each agent is unknown to others.
In this paper, the existing distributed optimization model is extended to a more complex one, where the global decision variable is a time-variant continuous function rather than just a vector.For each agent, its local objective is the integration of a non-convex function, which is known as the “functional”.These agents try to compute the decision function to minimize the sum of their functionals under privacy protection.The proposed problem is referred to as the minimization of the non-convex objective functionals of multi-agent network.
Most of the existing works [11]–[15] involving distributed optimization focus on the distributed gradient manner, where the agents reach the consensus to the optimal solution through communication with neighbors and the gradient information of its local function.Reference [11] combines the push-sum protocol with a distributed inexact gradient method to solve the distributed optimization problem.Reference [12] raises two bounded distributed protocols to address a global optimal consensus problem.However, these works are concerned with the minimization of the smooth and convex function.When it comes to the non-convex function, the global minimizer cannot be obtained through a derivative.Moreover, the decision variable in the above work is a vector.In contrast, our decision variable is a continuous time-variant function.Hence, the local change of the functional is represented with the variation rather than differential.Thus, these works cannot be directly applied to our problems.
Since the overall objective in our problem is the integration of a time-variant function, this problem behaves as a similar feature of a distributed online optimization problem.In[16]–[21], the agents aim to minimize the regret, which quantifies the error between the accumulated time-variant cost and the best-fixed cost knowing the overall objective functions in advance.In [22]–[25], the overall objective also behaves as the feature in the sum of the time-varying cost functions.The existence of the ramp-rate constraint increases its complexity.However, their decision variable is in the form of the discrete function, which means the amount of the variables is finite.In contrast, our decision variable is a continuous function over a bounded time interval.Since this kind of interval is uncountable [26], the amount of the variables is infinite.Moreover,our objective functional takes into account the influence of the derivative of the decision function.Therefore, these works cannot deal with our problem either.
The minimization of the overall objectives in this paper is essentially a problem in the calculus of variations (CVs).The core of CVs is mainly concerned with the solutions for the Euler-Lagrange (EL) equation.Due to unknown global information and non-convexity, the proposed problem in this paper is a complicated partial differential equation (PDE).Hence,we do not attempt to directly seek the decision function.Instead, a linear integral system is made up.In view of this system, the derivative of the decision function is regarded as the control input.Then instead of seeking a function to minimize the functional, we seek to obtain the optimal control input to minimize the cost function, which is essentially an optimal control problem [27].Each agent has its local cost function known only to itself.The target is to obtain the consistent optimal control input to minimize the sum of the cost functions of these agents under privacy protection.
Solving the optimal control problem is usually transformed into obtaining the optimal value function of the corresponding Hamilton-Jacobi-Bellman (HJB) equation [28].However,it is still challenging to solve due to the coupling between the control input function and the value function.To handle this,policy iteration (PI) [29] in reinforcement learning (RL) [30]is a valid technique.Therefore, we propose a centralized RL framework to obtain the centralized solution without the demand of solving a complicated PDE.The proposed RL framework is relevant to [31]–[35] that also apply RL to acquiring the solution of the HJB equation.However, these works have not considered privacy protection.
Considering the existence of privacy protection, we further design a distributed RL framework.In each iteration of this framework, the agents cooperatively evaluate the value function and update the control input.For value function evaluation, each agent approximates the value function through a time-varying neural network.Therefore, a static distributed optimization problem is generated to evaluate the value function at every time instant.A continuous protocol is designed to make the agents reach a consensus on the value function based on their local information.To update the control input cooperatively, these agents estimate the control input function at every time instant.Similarly, another continuous protocol is designed for the agents to update the control input cooperatively.The centralized RL framework and the two protocols make up the distributed RL framework.
The main contributions of this paper are as follows.
1) This paper raises a novel distributed optimization problem.Existing works involving distributed optimization seldom concern the difficulty in the time aspect where the decision variable is a time-varying continuous function.Moreover,our objective functional is the integration of a non-convex function over a continuous time interval.
2) Since the EL equation of the proposed problem is a complicated PDE difficult to solve, we convert the optimization of the functional into an optimal control problem.Then, the relationship between distributed optimal control and distributed optimization is built in this paper.Based on the transformed problem, this paper proposes a centralized RL framework.
3) To eliminate the influence caused by privacy protection,this paper further puts forward a distributed RL framework.The convergence analysis is also provided.
The structure of this paper is organized as follows.In Section II, some preliminary knowledge is given.Then, problem formulation for the proposed problem is represented.Section III illustrates problem transformation into the distributed optimal control problem.Section IV proposes a centralized RL framework for the transformed problem in Section III.Based on the centralized RL framework in Section IV, Section V raises a distributed RL framework for the agents.Section VI reveals the simulation result of our framework.Finally, conclusions and future orientation are stated in Section VII.
II.PROBLEM FORMULATION FOR THE NON-CONVEX OBJECTIVE FUNCTIONALS OF MULTI-AGENT NETWORK
This section firstly introduces some preliminary knowledge.Then the exact problem formulation for the non-convex objective functionals of the multi-agent network is given.
A. Preliminary Knowledge
Our preliminary knowledge mainly involves relevant graph theory, static distributed optimization, and the calculus of variations.

3)Calculus of Variations: The functional can be understood as a particular function whose domain of definition is composed of several continuous functions.For any functionx(t)in its domain of definition, there exists a unique real number that corresponds tox(t).The functional can be regarded as“the function of an function”.The mathematical model of a typical functional can be expressed as follows:
wherex(t)∈Rnis a continuous vector function with respect tot, and its first-order derivative isx˙(t).g(·) andh(·) are scalar functions.In this paper,t0,x0, andtfare fixed.
Calculus of variations is the origin of functional analysis in mathematics, and it is a method that aims to seek the decision function to optimize the functional.According to the definition in (2), the mathematical model can be expressed with
wherex(t) is the decision function.
The overallx(t) fromt=t0tot=tfcan be understood as a“special” vector.We know from functional analysis that the bounded interval [t0,tf] is uncountable, therefore this special vectorx(t) is with infinite dimensions.
B. Non-Convex Objective Functionals of Multi-Agent Network
Now a network composed of multi-agents withNnodes is given.The topology of this network is represented by the graphG.For the agenti(i=1,2,...,N) in this network, it is equipped with its local functional known only to itself
Remark 1: The functional (4) of the agentimaps the functionx(t),t∈[t0,tf] to a real number.The agents in this network share the same decision functionx(t).However, there is privacy protection where each agent only knows its own functional.
Assumption 1: In this paper, the functional (4) of the agentihas the following form:
where symmetric matricesRi>0 , andQi(x),hi(x) of some agentiare non-convex continuous functions.
Under privacy protection, each agent aims to communicate with its neighbour to find the consistent decision functionx(t)such that the sum of these functionalsJi(x(t)) is minimized.That is
Based on Assumption 1, the sum of these functionals is also non-convex with the following form:


III.PROBLEM TRANSFORMATION INTO DISTRIBUTED OPTIMAL CONTROL PROBLEM
The minimization of the overall objective functional in (6)is essentially a problem in the calculus of variations.The Euler-Lagrange (EL) equation for (6) is a complicated PDE.Moreover, non-convexity and privacy protection bring more difficulties of solving (6).This section mainly discusses how to handle non-convexity by converting the problem (6) to a distributed optimal control problem.Furthermore, this transformation is also the basis of the RL frameworks in the following two sections.
A. The Relationship Between Calculus of Variations and Optimal Control
According to the mathematical model defined in (2), the decision variable of the functionalJ(x(t)) is a functionx(t),which is essentially a trajectory starting fromx(t0)tox(tf).Its derivative functionx˙(t) can be regarded as its dynamics.Therefore, we regardx(t) as the system trajectory of the following control system:
whereu(t)∈Rnis the control input of this system.As long as the control inputu(t),t∈[t0,tf] is given, the corresponding system trajectoryx(t) can be generated.Therefore, the functionalJ(x(t)) in (2) could be transformed into
The value ofV(x0,u(t)) is essentially the same as that ofJ(x(t)).Since (9) can be regarded as the cost function for system (8), the minimization forJ(x(t)) is essentially the following optimal control problem:
As long as the optimal control inputu(t) for (10) is obtained, the system trajectoryx(t) together with its derivative functionx˙(t) , i.e.,u(t) can minimize the functional (2).Therefore, the minimization of (2) is transformed into the optimal control problem (10).
B. Distributed Optimal Control Problem
According to the discussion about optimal control, we can transform the minimization problem (6) into the following distributed optimal control problem.
For the linear system given by (8), each agent in the networkGis equipped with its own cost function unknown to other agents
With Assumption 1, the cost function for each agentiis represented with
Under privacy protection, the agents aim to find the consistent optimal control policyu∗(t) such that the sum of their cost functions can be minimized, that is
Remark 3: The transformed problem (13) belongs to a distributed control problem.However, this problem represents distinct philosophies compared with existing works [36], [37].The distributed control problems discussed in [36], [37]mainly concern the optimal control problem of large-scale interconnected systems.The distributed concept represented in the above works mainly lies in the decomposition of the large-scale system.Differently, the distributed concept shown in our problem (13) emphasizes more on the decomposition of the overall cost function.Due to privacy protection, the cost functionVi(x0,t0,u(t)) of agentiis unknown to other agents.The methods in the above works [36], [37] can not deal with the problem (13).
C. Centralized Solution for Distributed Optimal Control
Before solving the distributed optimal control problem (13),this subsection gives the property of the global solution.Similar to (7), the overall cost function is
Rewriting the minimization of the cost function (14) as
Similarly, we have
According to the Bellman principle of optimality, we have
WhenTis small enough, we have the Bellman equation
The corresponding Hamiltonian function is defined as

Remark 4:The target of (6) is to seek the optimal functionx(t).However, the non-convexity inQ(x),h(x) results in difficulty solving (6).In contrast, this subsection transforms (6)into (13), and turns to seek the optimalu∗(t) for (13) by minimizingH(x,t,u,V∗) at each time instantt.Foru, the Hamiltonian functionH(x,t,u,V∗) is convex.This is the reason whyu∗(t) can be derived through (20) even thoughQ(x),h(x) is non-convex.Moreover, the transformation in this section is the basis of the following two RL frameworks, where solving a PDE is avoided.
IV.CENTRALIZED REINFORCEMENT LEARNING FRAMEWORK
Recalling the Bellman principle of optimality, the key to obtaining the optimal control policyu∗for (17) is to accurately approximate the structure ofV∗, i.e., the solution for the HJB (21).However, we cannot directly obtainV∗by (21).One reason is that (21) is still a complicated PDE in second order,and another reason is that the global message involvingQ(x),Ris unknown to all agents.In this section, we mainly introduce a centralized reinforcement learning framework to deal with the former concerns.
A. Centralized Policy Iteration Framework for Optimal Control Problem
The reason why (21) is a complicated PDE lies in the coupling betweenV∗andu∗.Equation (20) implies that if we aim to obtain the optimalu∗,V∗should be known in advance.The origin of the HJB (21) is (18) whereu∗is substituted with(20).Equation (18) implies that if we aim to obtain the optimalV∗in (18),u∗should be known in advance.This phenomenon seems to be a “chicken-and-egg” problem.
To deal with the coupling betweenV∗andu∗, this subsection considers policy iteration of reinforcement learning.Then, (17) becomes
with
With (23), (22) is equivalent to

Fig.1.The structure diagram for the centralized PI framework.


Algorithm 1 Centralized Policy Iteration Framework j=1 uj 1: Initialization.Set.Start with a stabilizing control input.uj 2: Value function evaluation.Apply the current control policy to the system (8).Measure the corresponding system state trajectory.Evaluate by x(t) Vj Vj(x(t),t)=h(x(tf))+■t f (t Q(x)+ujT Ruj)dτ.(26)uj+1(t)3: Policy update.Update the control policy by uj+1(t)=-1 2R-1 ∂Vj∂x.(27)j= j+1 //Vj-Vj-1//≤δ0 δ0>0 4: Set , and go to Step 2 until where is a constant and is known as the cyclic tolerance error.
Remark 5: Reference [38] proposes the similar algorithm,and proves its convergence.However, when the global messages aboutQ,Rare unknown, the value function evaluation step in these algorithms cannot be directly implemented.This is also the motivation of the distributed algorithm in Section V.
B. Centralized Reinforcement Learning Framework With Value Function Approximation
For convenience, we denoteVj(x(t),t) asVj(x,t).The structure of Algorithm 1 is given in Fig.1.
The key for Algorithm 1 is determining how to evaluateVjin Step 2.Therefore, this subsection first approximatesVj(x,t)in (26) using the neural network with time-varying weights.That is
Based on (28), we have
Based on (28) and (29), Algorithm 1 becomes Algorithm 2.

Algorithm 2 Centralized Reinforcement Learning Framework With Value Function Approximation j=1 uj 1: Initialization.Set.Start with a stabilizing control input.uj 2: Value function evaluation.Apply the current control policy to the system (8).Measure the corresponding system state trajectory.Evaluate in by x(t) ˆWj(t) Vj ˆWj(t)T σ(x)=h(x(tf))+■t f (t Q(x)+ujT Ruj)dτ.(30)uj+1(t)3: Policy update.Update the control policy by[∂σ(x)]T uj+1(t)=-1 2 R-1∂x ˆWj(t).(31)j= j+1 //ˆWj- ˆWj-1//≤δ1 δ1>0 4: Set , and go to Step 2 until where is a constant and is known as the cyclic tolerance error.
Remark 6: In thej-th iteration of this framework, seeking the structure ofVjis transformed into seekingWˆj(t).
V.DISTRIBUTED REINFORCEMENT LEARNING FRAMEWORK
Algorithm 2 only settles the first concern that (21) is a complicated PDE in the second order.However, the second concern about privacy protection implies that the global message abouth(x(tf),tf),Q(x),Ris unknown for all the agents.Therefore, Steps 2 and 3 of Algorithm 2 can not be directly implemented under this privacy protection.To deal with this concern, this section introduces the distributed reinforcement learning framework.
A. Distributed Solution for Step 2 in Algorithm 2


At time instantt, the agentiestimatesθasθi∈Rlwith the corresponding equality constraint and the penalty item in the optimization function.On the basis of (36), the exact problem becomes
whereLis the Laplacian matrix of the graphG, and
According to [39], we know that the solution to the problem (37) is the saddle point of its Lagrangian function.Similar to the procedure in [39], the continuous protocol for the agenticould be derived as

B. Distributed Solution for Step 3 in Algorithm 2
In Step 3 of Algorithm 2, the target is to update the new control policyuj+1.SinceRis unknown for all the agents, (31)in Step 3 cannot be directly implemented.For agenti, onlyRiis known to itself.It can only try to update the new control policyuj+1to minimize the following Hamiltonian function:

The problem (41) is also the standard form of the static distributed optimization problem in (1).Note that the value ofVj,Qi(x)is changing over time.Therefore, for each time instantt, there is a static distributed optimization problem(41), which is diverse from that of other time instants.
Similar to the procedure from (37) to (38), the continuous protocol for the agentiis

C. Distributed Reinforcement Learning Framework
The protocols (38) and (42) are implemented without the demand of the global message.Each agent only needs its own local message.Now their convergence and optimality is given.
Theorem 1: The protocol (38) could converge.When it converges, θireach the consensus toWˆj(t) for Step 2 of Algorithm 2.
Proof: See Appendix.
Similar to the proof for the protocol (38), the protocol (42)
uj+1 could converge, and the new policy for the Step 3 in Algorithm 2 could also be obtained when (42) converges.
Since the convergence and the optimality of the protocols(38) and (42) has been proved, Steps 2 and 3 in thej-th iteration of Algorithm 2 could be implemented in a distributed manner.Then we give the following Algorithm 3 according to the framework in Algorithm 2.

Algorithm 3 Distributed Reinforcement Learning Framework j=1 uj 1: Initialization.Set.Start with a stabilizing control input.uj 2: Value function evaluation.Apply the current control policy to the system (8).Measure the corresponding system state trajectory.For each time instant from to , the agent i calculates defined in (35).Then, its is updated through the protocol x(t) t=t0 t=tf yi θi d ˙θi [∇θi fi(θi)N∑N∑]dτ =-α N +aij(θi-θj)+aij(λi-λj)j=1 j=1 d ˙λi [ N∑]dτ =α aij(θi-θj).(43)j=1 ˆWj(t)When (43) converges, is determined through the consistent value of.3: Policy update.[t0,tf]k=1 t0 x(t0)=x0 θi 3.1: Discretize the time interval with a small time period T.Set.For the initial time instant , is given.t=t0+(k-1)T ˆWj(t)x(t) ∂Vj 3.2: At the time instant , based on obtained in Step 2 and the current state , for the time instant t is obtained.The agent i is equipped with its own , and the initial value of is set as.Then, the agent i calculates its own, and updates its through the protocol∂x =[∂σ(x)∂x]T ˆWj(t)ρi ρi 0∇θi Hi(ρi)=2Riρi+ ∂Vj∂x ρi d ˙ρi [∇ρi Hi(ρi)N∑N∑]dτ =-β N +ai j(ρi-ρj)+aij(ηi-ηj)j=1 j=1 d ˙ηi [ N∑dτ =βaij(ρi-ρj)].(44)j=1 uj+1(t)ρi When the protocol (44) converges, is determined by the consistent value of.uj+1(t)x(t+T) k=k+1 t=t0+(k-1)T t=tf 3.3: Apply the updated to system (8) to generate the new state.Let , and go to Step 3.2 until.j= j+1 //ˆWj- ˆWj-1//≤δ2 δ2>0 4: Set , and go to Step 2 until where is a constant and is known as the cyclic tolerance error.

VI.NUMERICAL SIMULATION
In this section, the simulation results of Algorithm 3 are mainly discussed.The agents are distributed over the network in Fig.2 whose graph is represented with the following adjacency matrix:

Fig.2.The topological graph of the agents.

For the agenti∈{1,2,3,4}, its objective functionalJimaps the decision functionx(t) to a real number.These agents aim to minimize their overall functional

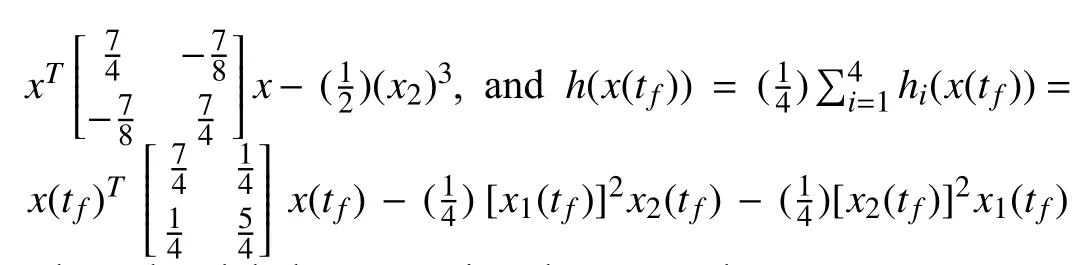
where the global message is unknown to the agents.
To seek the optimal decision functionx(t) minimizing (47)in a distributed manner, the following linear system is considered:
whereu(t)∈R2is the control input of this system.Then, the minimization for (47) is transformed into seeking the optimal control inputu∗(t) to minimize
The minimization of (49) is essentially an optimal control problem.Its HJB equation is
Since the agentionly knows its local messageQi,Ri,hiinQ,R,h, the optimal solution cannot be obtained by solving(50) directly.That is why we propose Algorithm 3 to deal with this problem.
Now, we show some settings before implementing our Algorithm 3.In thejiteration of this algorithm, the agents desire to cooperatively obtainmaking up the value functionVj=σ(x) that satisfies the HJB (50) as possible.For this problem, the basis function σ (x) is selected as
and the exact structure of the time-varying NN weights is



Fig.3.The convergence tendency of the first nine elements of

Fig.4.The convergence tendency of the last element of




Fig.5.The convergence of the error functionalEw(Wˆj(t)).

Fig.6.The exact procedure of how the agents reach the consensus to the consistent W ˆj,6(t) for the j=5 iteration.

Fig.7.The exact procedure of how the agents reach the consensus to the consistent W ˆj,8(t) for the j=5 iteration.

Fig.8.The exact procedure of how the agents reach the consensus to the consistent u j+1,1(t) in the new control policy of the j=5 iteration.
VII.CONCLUSIONS AND FUTURE ORIENTATION
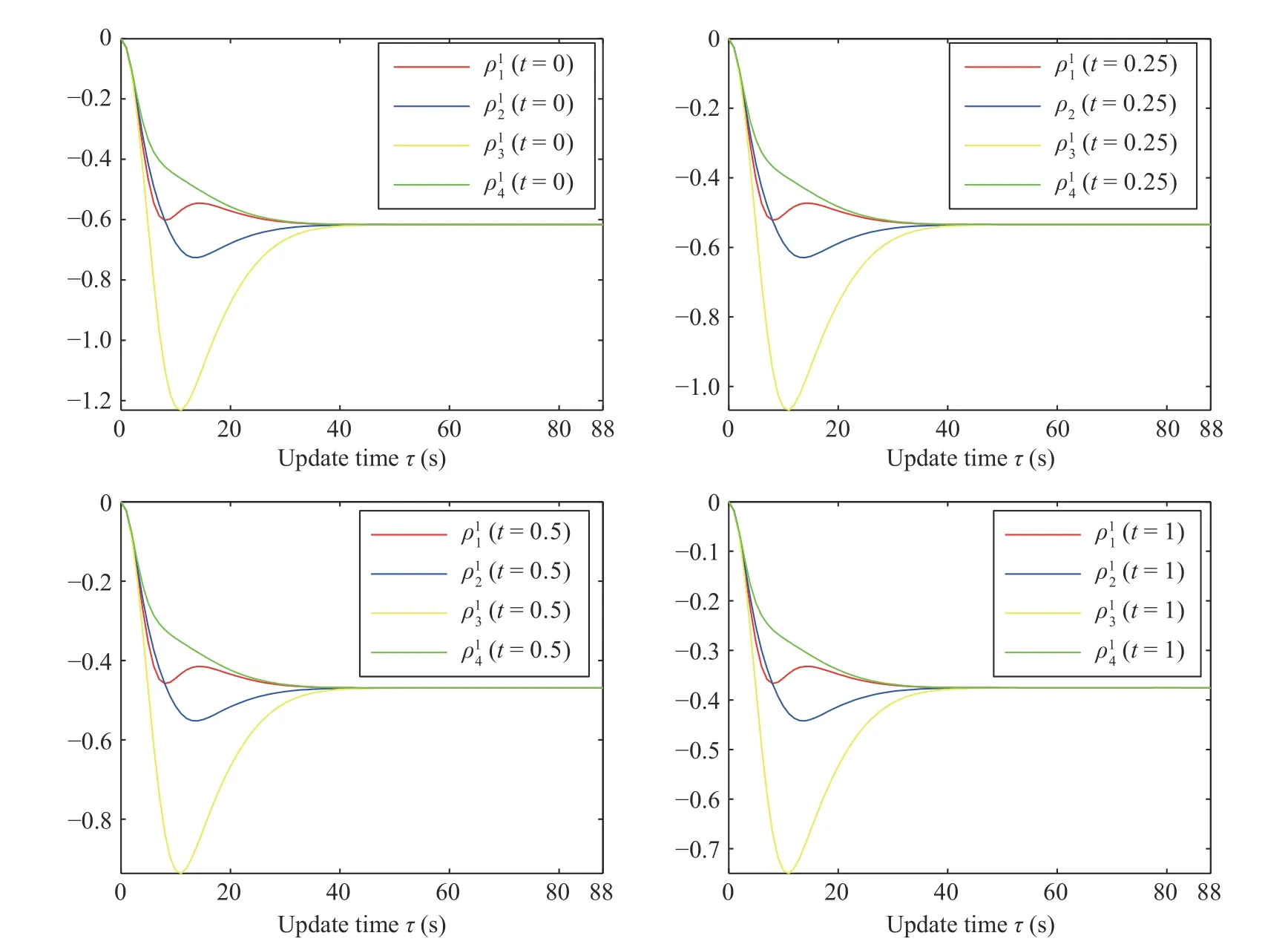
Fig.9.The exact procedure of how the agents reach the consensus to the consistentuj+1,1(t) at different time instants.
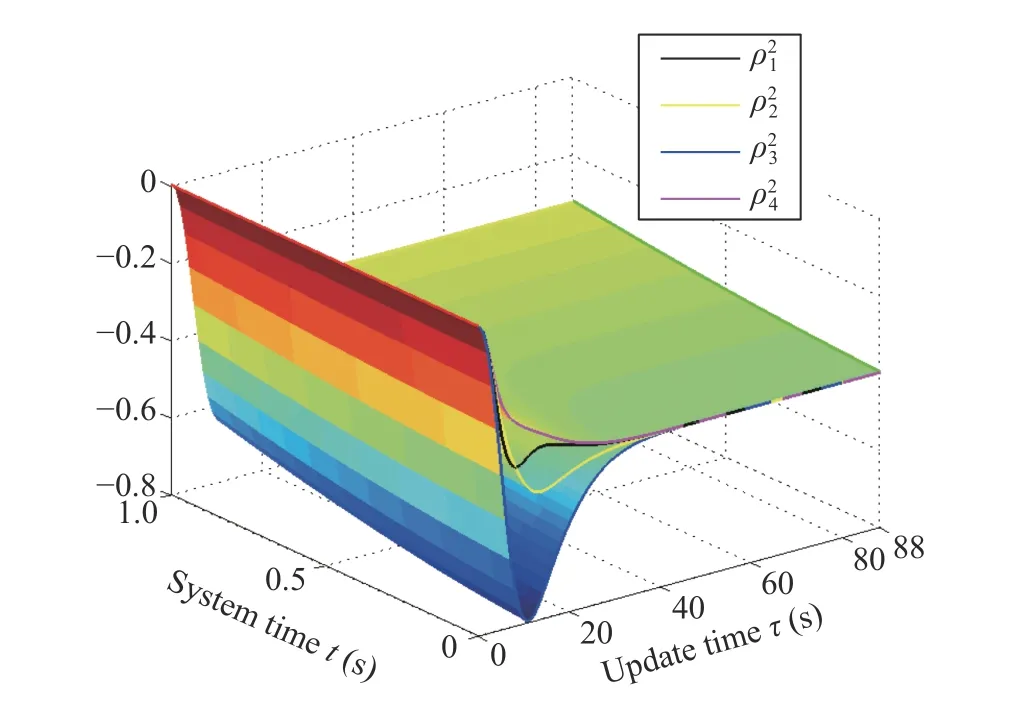
Fig.10.The exact procedure of how the agents reach the consensus to the consistent u j+1,2(t) in the new control policy of the j=5 iteration.
This paper studies a novel distributed optimization problem,where each agent is equipped with a local functional unknown to others.Besides the privacy protection discussed in the existing works about distributed optimization, the proposed problem involves the difficulty in the time aspect that the decision variable is a time-varying continuous function.Especially, the functionals of some agents are non-convex.Considering privacy protection and non-convexity, we transform the proposed problem into a distributed optimal control problem.Then, we propose a centralized RL framework to avoid solving a PDE directly.What’s more, we further put forward a distributed RL framework to handle the presence of privacy protection.The numerical simulation verifies the effectiveness of our framework.In the future, we will discuss a more representative case than that in Assumption 1.
APPENDIX PROOF OF THEOREM 1
Proof(Stability): For convenience, we analyze the matrix form of (38)

Differentiating both sides of (59) with respect to the update timeτ, we have
Differentiating both sides of (58), we have
Substituting (61) into (60) yields
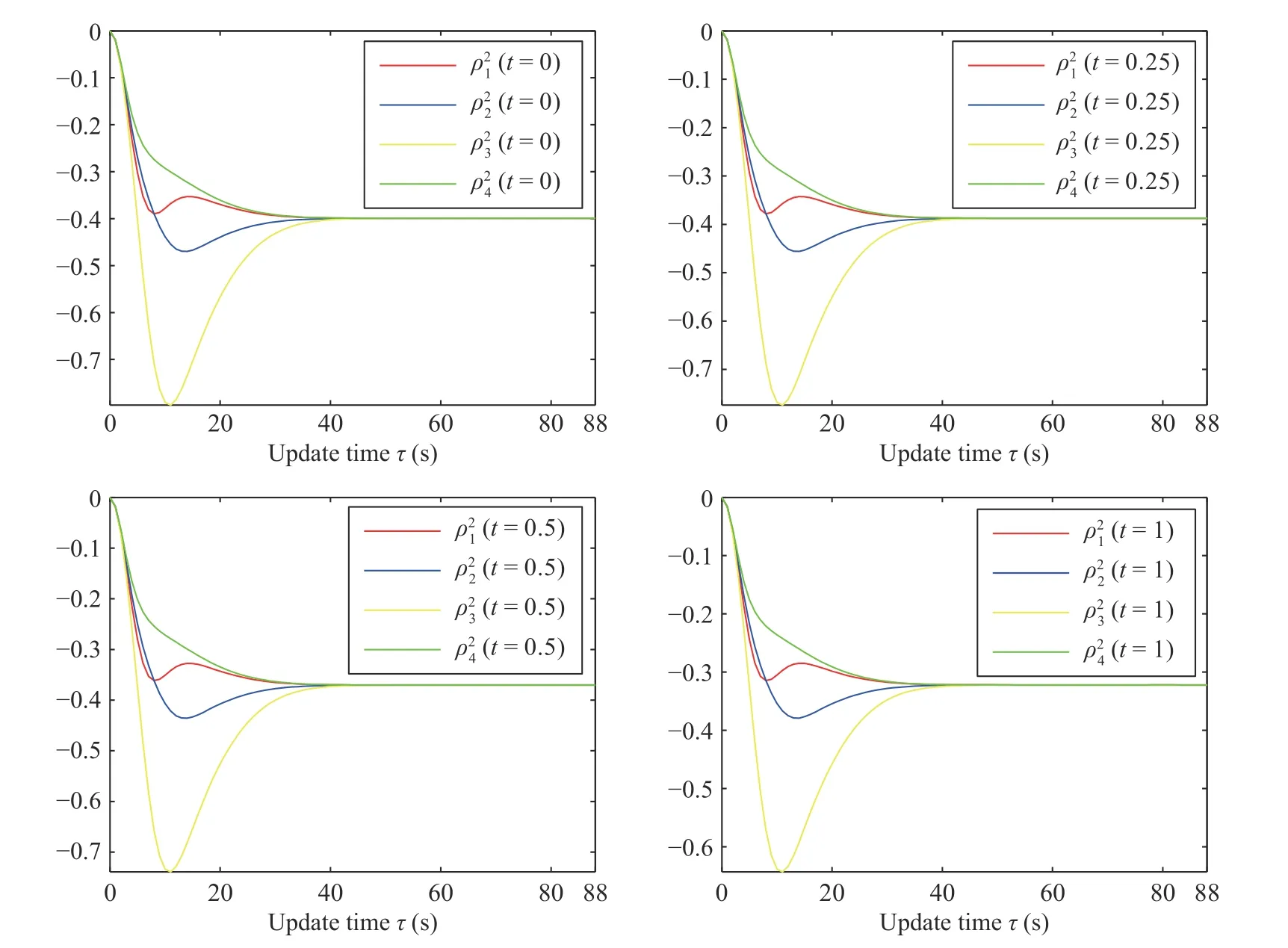
Fig.11.The exact procedure of how the agents reach the consensus to the consistentuj+1,2(t) at different time instants.

Fig.12.The optimal decision functionx∗(t) cooperatively obtained by the agents.
Considering (33) and (35), we have
Therefore,
Since (59) has implied ς is positive semi-definite, (58) will converge.
Proof(Optimality): The convergence of (38) has been proved.When it converges to the equilibrium point, we have
Based on (65), we have
and
Adding up (67) fromi=1 toi=N, we have
Therefore, the consistentθ, or equivalentlyWˆj(t) is the optimal solution for (34).Moreover, based on (68), (33), and (35),we have
Therefore, the consistentθsatisfies (30) in Step 2 of Algorithm 2.
 IEEE/CAA Journal of Automatica Sinica2023年11期
IEEE/CAA Journal of Automatica Sinica2023年11期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Multi-Objective Optimization for an Industrial Grinding and Classification Process Based on PBM and RSM
- Containment-Based Multiple PCC Voltage Regulation Strategy for Communication Link and Sensor Faults
- GraphCA: Learning From Graph Counterfactual Augmentation for Knowledge Tracing
- Adaptive Graph Embedding With Consistency and Specificity for Domain Adaptation
- The ChatGPT After: Building Knowledge Factories for Knowledge Workers with Knowledge Automation
- Can Digital Intelligence and Cyber-Physical-Social Systems Achieve Global Food Security and Sustainability?
