Disturbance Observer-Based Safe Tracking Control for Unmanned Helicopters With Partial State Constraints and Disturbances

Haoxiang Ma, Mou Chen,,, and Qingxian Wu

Abstract—In this paper, a disturbance observer-based safe tracking control scheme is proposed for a medium-scale unmanned helicopter with rotor flapping dynamics in the presence of partial state constraints and unknown external disturbances.A safety protection algorithm is proposed to keep the constrained states within the given safe-set.A second-order disturbance observer technique is utilized to estimate the external disturbances.It is shown that the desired tracking performance of the controlled unmanned helicopter can be achieved with the application of the backstepping approach, dynamic surface control technique, and Lyapunov method.Finally, the availability of the proposed control scheme has been shown by simulation results.

I.INTRODUCTION

IN recent decades, much attention has been attracted in the unmanned aerial vehicle (UAV), especially the unmanned autonomous helicopter (UAH), and much research has been reported [1]-[4].With the continuous development of UAH,the applications of medium-scale unmanned autonomous helicopters have been widely popularized in civilian and military fields, respectively [5]-[9].For the flexibility and effectiveness of the design, a specific backstepping approach was introduced for a six degrees of freedom (6-DOF) UAH system in [10].However, these feedback backstepping control schemes may result in the problem of computation burden due to repeated differentiation of virtual controllers.To overcome this problem, the dynamic surface control (DSC) technique was introduced in [11], and widely utilized in many feedback backstepping control problems [12]-[15].Combined with the radial basis function neural network, a DSC scheme was investigated for uncertain strict-feedback nonlinear systems in[16].In this paper, the first-order DSC is adopted to avoid the repeated differentiation of the virtual controller.Besides, during practical flight, the UAH is usually subjected to constraints of partial states, such as flight path, attitude angles,and flapping angles.

It is worth noting that these constraints are time-varying for executing some special missions such as geological prospecting in narrow spaces [17] and forest fire monitoring [18].Determining how to follow the original desired signal as far as possible on the basis of avoiding conflict with state constraints was developed in various methods, such as model predictive control (MPC) [19], the barrier Lyapunov function(BLF) method [20]-[24], the prescribed performance function (PPC) method [25], etc.Suzakiet al.[26] studied a model predictive controller for small unmanned helicopters to avoid collision.A barrier Lyapunov function based trajectory tracking controller was investigated for miniature unmanned helicopters flying in a narrow space [27].By combining this with a prescribed performance function, the authors in [28] designed an adaptive neural network controller for an UAH system with output constraints.Besides, a reactionary boundary protection method [29] was developed to calculate a new constrained desired trajectory for an unmanned helicopter [30].Considering the practicality and feasibility, the constraints of flight path, attitude angles, and flapping angles are taken into account for the UAH system in this paper.Enlightened by the reactionary boundary protection method, this paper proposes a safety protection algorithm (SPA) to tackle the time-varying partial state constraints obtained by sensors [31] and smoothing methods [32], [33].By calculating new safe desired trajectories which satisfy the partial state constraints, the system is expected to track them to keep every constrained state within the given constraint scope.Besides the partial state constraints,the unknown external disturbances need to be considered during the real-time flight of the UAH.

In order to improve the disturbance rejection performance of the UAH system, a lot of control methods have been investigated in recent decades, such as active disturbance rejection control (ADRC) [34], [35], adaptive control [36], extended state observer-based control [37], and disturbance observerbased control (DOBC) [38]-[40].Due to the online estimation ability of DOBC, many kinds of disturbance observers combined with other techniques have been further studied.For instance, sliding mode disturbance observers [41], fixed-time disturbance observers [42], adaptive disturbance observers[43], high-order disturbance observers [44], etc.In [45], a second-order disturbance observer (SODO) was adopted to compensate for complex disturbances.Inspired by this, to achieve the unbiased estimation of the time derivative of the disturbance, the SODO was developed in the paper.

In this paper, a SODO-based safe tracking controller is developed for the unmanned helicopter with rotor flapping dynamics in the presence of partial state constraints and unknown external disturbances by exploiting backstepping and DSC.The main contributions are illustrated as follows:

1) To handle the time-varying partial state constraints of the UAH, a SPA is proposed to generate the safe desired trajectories.A first-order DSC technique is utilized to deal with the piecewise differentiability of the safe desired trajectories.

2) A developed second-order disturbance observer method is investigated to estimate the disturbances, and the unbiased estimation of their time derivatives is achieved.

3) The closed-loop system convergence is guaranteed by the Lyapunov method, which shows that all closed-loop system signals are bounded.Namely, the UAH system can track the generated safe desired trajectories and satisfies partial timevarying state constraints.

The rest of this paper is organized in the following parts.Section II details the modeling of the UAH system with flapping dynamics and problem formulation.The SODO-based safe tracking control scheme is investigated in Section III.The simulation results are presented in Section IV to demonstrate the effectiveness of the proposed controller and Section V concludes the paper.

Notations:f(r)(·) stands for therth order time derivative of the functionf(·), andf(0)(·)=f(·).For a matrixA,//A//denotes the Euclidean norm or Frobenius norm, andA>0 means thatAis a positive definite matrix.Iirepresents the identity matrix withidimensions, and 0 represents the zero matrix or vector with compatible dimensions.

II.PROBLEM FORMULATION AND PRELIMINARIES

In this section, the 6-DOF full state model of a mediumscale UAH in the presence of time-varying partial state constraints and external unknown disturbances is described, and the problem is illustrated in detail.

A. Modeling of the UAH System

For convenience, two reference frames are defined as the inertial frame ℜeand the body-fixed frame ℜb.According to the flight dynamics and aerodynamics, the 6-DOF nonlinear model of a medium-scale UAH with external unknown disturbances can be expressed as [4]

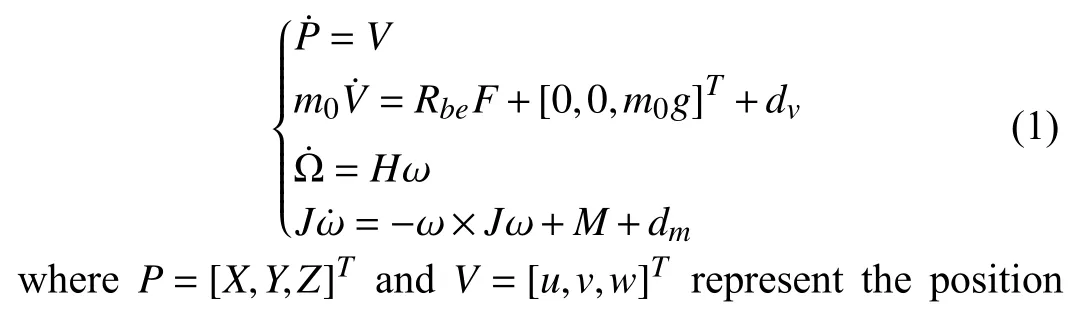
and

Generated by the tail rotor, the control force moment vectorMis given by [1]

B. Rotor Flapping Dynamics

The cyclic flapping dynamic model, that contains the longitudinal flapping angleaand lateral flapping angleb, can be represented by the following first-order equations [4]:

whereAlon,Blatand τa, τbdenote the effective steady-state gains,Ta,Tbdenote the longitudinal and lateral main rotor time constant, respectively,TaandTbare the longitudinal and lateral cyclic control inputs, andda,db∈R denote the timevarying external unknown disturbances in the rotor flapping loop.

Considering the external unknown disturbances of the main rotor, the flapping dynamics model Θfcan be rewritten as

where

C. Problem Formulation

Generally, in order to achieve mission objectives, the original reference flight trajectoryPdis formulated without considering various constraints.However, since the geographical conditions, the attitude constraints and the flapping dynamic limitations universally exist during most flight missions, it is of great significance to take the time-varying partial state constraints of the UAH into account.

Control objective:

1) Design a safe tracking controller to ensure all the variables involved in the resulting closed-loop system are uniformly ultimately bounded (UUB);

2) On the basis of tracking the original reference flight trajectoryPd=[Xd,Yd,Zd]Tas far as possible, every constrained state satisfies corresponding time-varying partial state constraints, that is, ∀t≥0,

wherex∈{X,Y,Z,ϕ,θ,ψ,a,b} denotes the constrained state in the UAH system.

Furthermore, to design a safe tracking controller of the UAH system (1) with time-varying partial state constraints and unknown external disturbances, the related assumptions are given as follows.

Remark 1:Generally speaking, the boundary information can only be obtained by an airborne sensor real-time scanning measurement.The time-varying partial state constraints in this paper is based on the sampling points of the boundary information obtained by sensors, and processed by the relevant smoothing methods, such as the B-spline curve method [32],interpolation fitting method [33], etc., which has real-time,smoothness and boundedness.

III.SODO-BASED SAFE TRACKING CONTROLLER DESIGN

In this section, to satisfy time-varying partial state constraints, the SPA is proposed to generate a safe desired trajectory.Since the safe desired trajectory is piecewise differentiable and using the phenomenon of repeated differentiation,DSC technology is utilized in the safe tracking problem.The SODO is introduced to estimate the disturbance and the upper bound of the derivative of disturbance.A second-order disturbance observer-based safe tracking control scheme is designed to ensure the convergence of the UAH system.

A. Calculation of the Safe Desired Signals

where β>2 is a design constant related to the following controller design.

It follows from (9) and (10) that the inequality:

Secondly, we define the following increments:

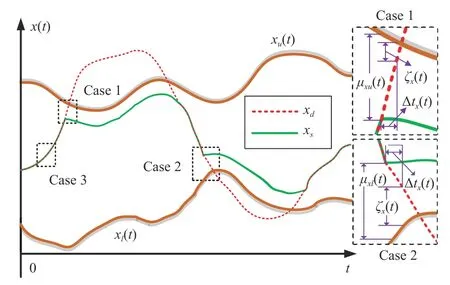
Fig.1.A new safe trajectory xs(t) obtained by SPA.

wherez∈{d,u,l}.

It follows from (12) and Fig.1 that the predictive marginsµxu(t) , µxl(t) can be obtained by:

The generation of the safe trajectoryxsobtained by SPA is shown as Fig.1.Through discussing whether the safety boundary violation (SBV) is predicted after ∆tx(t), the judging criteria of SPA can be described as a diagram in Fig.2,and the calculations of various cases have been presented as follows:

Case 1: In this case, we consider thatxd(t) will violate the upper state constraint with ςx(t) at timet+∆tx.Thus, the safe trajectory signalxsneeds to be reset as

Case 2: Similar to Case 1, at timet+∆tx(t),xd(t) is going to violate the lower state constraint with ςx(t) in such a case.xsis given by

Case 3: The system will normally track the original trajectoryxdin this case.Namely, we can obtain that

Fig.2.The diagram of the safe protection algorithm for xd(t).

Remark 5: Referring to Fig.1 and the computation rule of SPA, the variation tendency of the generated safe desired signals might be suddenly changed.To deal with this problem, a first-order filter is adopted to smooth the safe desired signals in this paper.On this basis, we consider that the flexibility of UAH can satisfy the control requirements without taking the constraints of the main rotor and tail rotor into account.

B. SODO-Based Safe Tracking Controller Design of the Position Loop

In this section, a safe tracking controller of the position loop will be proposed based on the SPA, DSC and SODO.

First, recalling Assumption 3 and Proposition 1, there exist positive constants κPsuch that //P˙s//≤κPfor the given initial conditions.

To deal with the piecewise differentiability of the safe flight trajectoryPs, letPspass through a first-order filter λPwhich is constructed as [11]

whereKλ1>0 ∈R3×3represents a design diagonal positive definite matrix.

Definingλ˜1=λP-Ps, one has

Design the tracking error vectors as

The virtual control lawVdis designed as

whereK1denotes a positive definite matrix to be designed.

Considering (2), (24), and (25), we have

To avoid repeated differentiation ofVd, letVdpass through a first-order DSC constructed as

whereKλ2∈R3×3represents a positive definite diagonal matrix.

Definingλ˜2=λV-Vd, one has

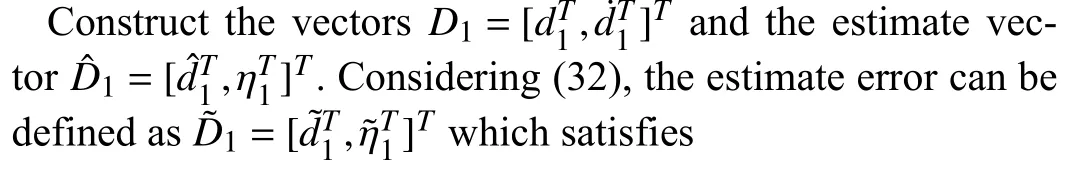
where

Based on the SODO (31), the original controller Σdis designed by

Remark 6: Different with traditional SODO, the developed SODO (31) added a error terme2which leads to a cross termin (39).This cross term then can further compensate for the effects of disturbances.

Consider the following Yang’s inequalities:

where σd1>0 and σ1>0 are the constants to be designed.

Thus, (39) can be rewritten as

C. SODO-Based Safe Tracking Controller Design of the Attitude Loop

In this section, a SODO-based safe tracking controller is investigated for the attitude subsystem of the UAH.

First, considering (34) and (35),

whereKλ3∈R3×3represents a positive definite diagonal matrix.

Definingλ˜3=λΩ-Ωs, one has

Design the tracking error vectors as

The virtual control law ωdis designed as

whereK3denotes a positive definite matrix to be designed.

Considering the (3), (44) and (45), we have

To avoid repeated differentiation of ωd, let ωdpass through a first-order DSC constructed as

whereKλ4∈R3×3represents a positive definite diagonal matrix.

Definingλ˜4=λω-ωd, one has

Specially, we design the actual force moment controllerMas

D. SODO-Based Safe Tracking Controller Design of the Rotor Flapping Loop

In this subsection, considering the safe desired flapping angles (21), a SODO-based safe tracking controller of the rotor flapping loop is investigated.

Firstly, considering (54) and (55),

is sufficiently smooth function vector about a set compact for the given initial conditions [11].Namely, αd(t) and α˙d(t) are bounded for allt≥0.Recalling Assumption 3 and Proposition 1, there exist positive constants καsuch that //α˙s//≤καfor the given initial conditions.

To deal with the piecewise differentiability of the safe desired signal αs, let αspass through a first-order filter λαwhich is constructed as

whereKλ5∈R2×2represents a positive definite diagonal matrix.

Design the tracking error vector as

where λαdenotes the output of DSC to be designed with αsbeing the input.Recalling (6) and (63), we have

Similarly, to estimate the unknown disturbanced3and its time derivatived˙3, a SODO can be designed as follows:

where

E. Stability Analysis

For convenience, define

and

The boundedness and safety of all the signals in the resulting closed-loop system is proved in the following theorem.

Theorem 1: Consider the 6-DOF full state UAH system (1)with time-varying partial state constraints and external unknown disturbances satisfying Assumptions 1-4.To limit all states within the time-varying partial state constraints, the safe desired signals and their time derivatives are designed in(17).The filters are designed as (22), (27), (42), (47), and (61)to smooth the safe desired signals and avoid repeated differentiation.To estimate the disturbances, the SODOs are designed as(31), (51) and (65).Then, for bounded initial conditions, all closed-loop signals are UUB under the proposed SODO-based safe tracking controller.Furthermore, the UAH system is able to track original desired trajectory when SBV is not predicted,and satisfy the time-varying partial state constraints when SBV is predicted, respectively, by choosing appropriate parameters such that

Proof: Choose the candidate Lyapunov functionWas

Invoking (40), (59) and (70), taking the time derivative ofW, we have

Integration of (75) yields

IV.SIMULATION STUDY

In this section, the effectiveness of the proposed SODObased safe tracking control scheme is presented for a mediumscale UAH with state constraints and unknown external disturbances.The physical parameters of the medium-scale UAH are given in Table I [4].

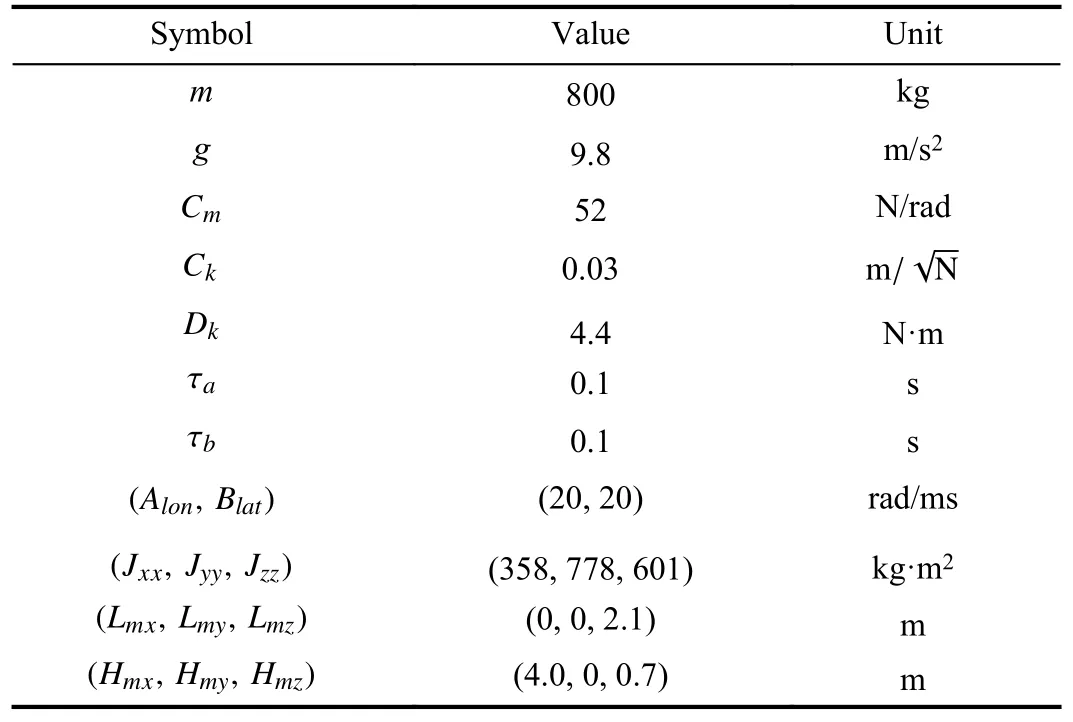
TABLE IPARAMETERS OF THE MEDIUM-SCALE UAH

In order to simulate the flight process of the UAH in the cave, the initial states, original desired trajectory, state constraints and external disturbances of this simulation are randomly set in Table II.

TABLE IIPREPARATIONS OF THE SIMULATION

Remark 7: Since the assumptive situation of this simulation is in a cave, we consider there are no constraints in the position onX-axis.To satisfy Assumption 5, the absolute value ofXuandXlis randomly set as a large one, such as 1 04m.

From the conditions above, the simulations can be obtained and expressed in Figs.3-14.

Fig.3.Tracking result of X with state constraints Xu and Xl.

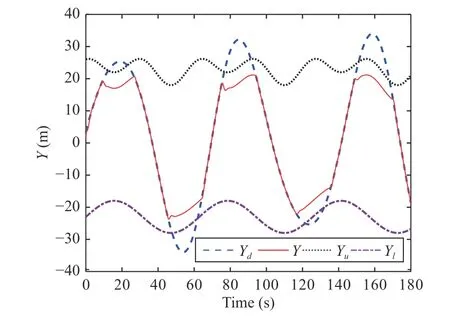
Fig.4.Tracking result of Y with state constraints Yu and Yl.

Figs.3-5 clearly show the flight tracking process when the UAH is passing through the cave, and the UAH system can realize the safety tracking response of the desired flight trajectoryPdwith state constraintsPu(t) andPl(t).The safety tracking response of the rest of the constrained states have been shown in Figs.6-9, which includes state constraints and unconstrained virtual signals.

For tracking the virtual controllersvd=[vxd,vyd,vzd]T,Ωd=[ϕd,θd,ψd]T, ωd=[pd,qd,rd]T, the tracking responses of these unconstrained states have been shown in Figs.10 and 11, which satisfy the tracking performance and the practicality of the designed control scheme.

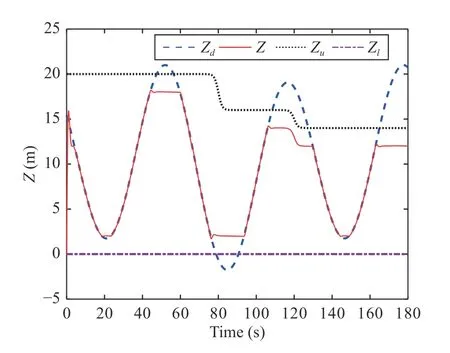
Fig.5.Tracking result of Z with state constraints Zu and Zl.

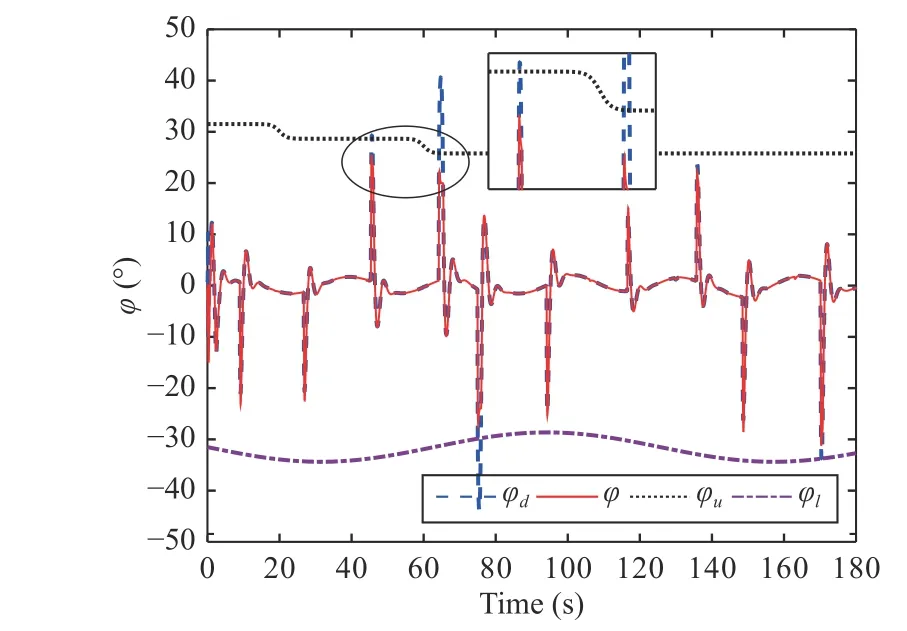
Fig.6.Tracking result of ϕ with state constraints ϕu and ϕl.

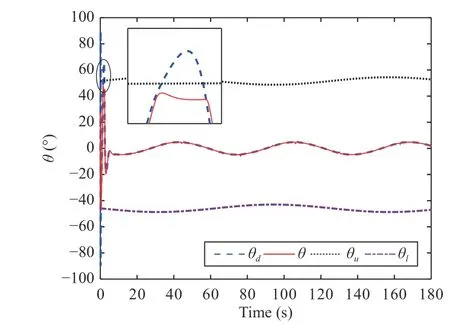
Fig.7.Tracking result of θ with state constraints θu and θl.

Fig.8.Tracking result of ψ with state constraints ψu and ψl.

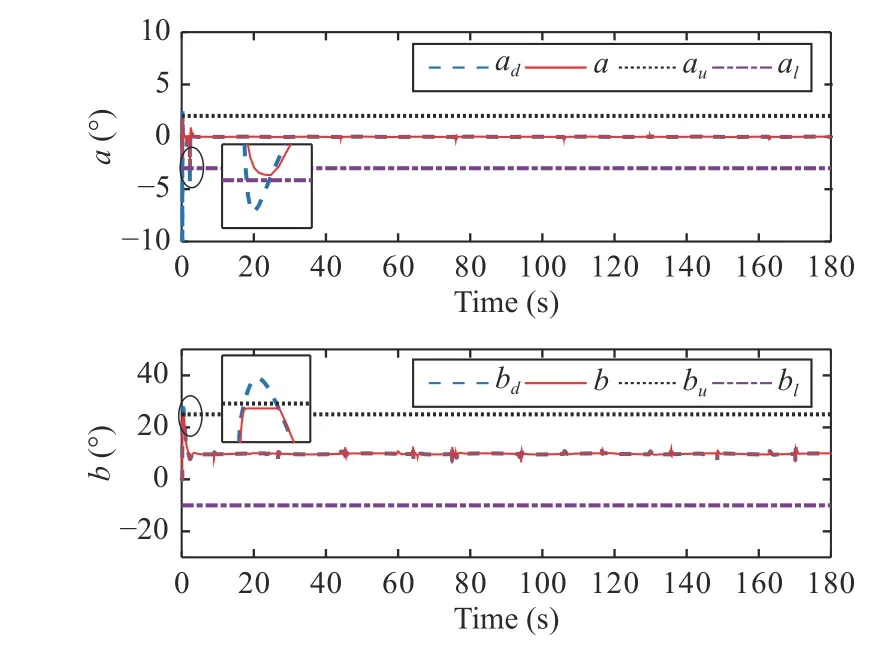
Fig.9.Tracking result of ψ with state constraints ψu and ψl.

Fig.11.Tracking results of the angular rates ω of the UAH.

Fig.12 shows the responses of the SODO-based safe tracking control inputs: the main rotor thrustTmr, tail rotor thrustTtr, and the longitudinal and lateral cyclic inputsTa,Tb.

The tracking responses of the SODOs are presented in Fig.13, which have classified the availability of the designed SODOs.

Fig.12.The response of SODO-based safe tracking control inputs.

Fig.13.Tracking responses of d1, d2, and d3 based on SODO.

In order to prove the effectiveness of the SPA and secondorder disturbance observer (SODO) designed in the proposed control scheme, Fig.14 is given by taking the constrained stateZas an example.Under the same control parameters and initial conditions as above, Fig.14 compares the tracking responses ofZwithout SPA or SODO, respectively.In Fig.14,although the response without SPA in gray can track original desired trajectoryZd, it conflicts with the constraintsZu,Zl,which leads to an irreversible accident.In addition, the response without SODO in orange cannot track the safety flight trajectoryZsin a reasonable range, which also may conflicts with the constraints.

Meanwhile, a reactionary boundary protection (RBP) method based control scheme [29] has been adopted to compare with the proposed control scheme in this paper.As shown in Fig.14, although the response with RBP in green satisfies the constraintsZu(t),Zl(t), the safety margin withZu(t) andZl(t)can not be guaranteed.On the contrary, the proposed control scheme in this paper is able to design the predictive marginsµxu(t) and µxl(t) in (13), which improves the safety of the proposed control scheme.

From the simulation results above, it can be concluded that the presented SODO-based safe tracking control scheme is effective and feasible for the UAH under the existence of the flight boundary constraints, uncertainties and external disturbances.

V.CONCLUSIONS

This paper purposes a SODO-based safe tracking control scheme for the unmanned helicopter system with main rotor flapping dynamics in the presence of partial state constraints and unknown external disturbances.A SPA is proposed to ensure the constrained states within the given safety scope.A SODO technique is utilized to estimate the external disturbances and their time derivatives.It is shown that the tracking performance of the controlled unmanned helicopter can be achieved by backstepping approach and the Lyapunov method.Finally, simulation results have been presented to demonstrate the effectiveness of the proposed scheme.