基于差分电压平台的锂电池自适应充电策略
段双明,董鹏来
(东北电力大学,现代电力系统仿真控制与绿色电能新技术教育部重点实验室,吉林 吉林 132012)
锂离子电池因具有能量密度高、循环寿命长、自放电率低和无记忆效应的优点,被广泛应用于移动设备、电动汽车、储能等领域[1-2]。然而,锂离子电池的充电过程存在多个问题,如小电流充电时间长、大电流充电易引起电池老化、过温等问题,限制了其在实际应用中的性能和可靠性[3]。因此,对锂离子电池的充电问题进行研究和优化具有重要意义。
传统的锂离子电池充电策略包括恒流恒压(CCCV)、恒功率(constant power,CP)及脉冲充电策略[4]。CC-CV充电策略易于实现、简单可控,已成为多数锂离子电池应用的标准充电策略[5]。然而,该策略在恒流阶段使用固定的经验电流值充电,优化变量单一,无法同时兼顾充电速度和电池寿命[6]。CP充电策略的充电电流会随电池电压动态变化,这会导致电池充电不均匀。同时,在电池电压达到较高水平时,充电电流可能会变得非常小,导致充电时间延长。脉冲充电策略在充电过程中会产生大电流脉冲,容易造成电池极化现象,影响电池使用寿命[7]。这些传统充电策略主要基于经验控制,无法根据电池内部的物理和电化学特性优化充电过程。因此,为克服这些局限性,众多国内外学者进行了改进研究。
为了实现更快速的电池充电,多阶恒流充电策略(multistage constant current,MCC)应运而生。相比于普通的恒流(CC)充电策略,MCC 由两个或更多个CC阶段组成,更为灵活多变。国内外研究表明,在充电过程中,通过调整电流值,可以有效降低电池温升、减小电池应力及充电损耗[8]。Zhao等[9]通过设立充电时间和SOH两个目标函数,分析比较了不同权重、不同截止电压和不同恒流阶段数对充电优化的影响。Jiang等[10]基于田口法进行正交实验,以充电容量、充电效率和充电时间为优化目标,得到基于截止电压的多阶恒流(VMCC)充电策略。与传统的CC-CV 充电策略相比,该策略可以在充电容量基本相同的条件下提高充电效率并降低电池温升,但该方法需要进行大量正交实验,求解过程较为复杂。Li等[11]以充电时间和SOH为优化目标,基于电-热-老化耦合模型提出了一种多阶段恒流恒压(multistage constant current-constant voltage,MCCCV)充电策略。该策略在电池的荷电状态(state of charge,SOC)达到预设阈值时切换到CV 充电模式,并维持恒定电压进行充电,直到充电过程结束。由于存在CV阶段,该方法较MCC充电策略会延长充电时间。Jiang 等[12]根据SOC 的变化将充电过程分段,并利用遗传算法优化充电电流。在优化过程中,他们发现SOC 超过70%后,相比CV 充电会增加损耗。由此限制,充电策略较早进入CV阶段,这不利于快速充电的需求。
上述研究基于不同的恒流切换条件划分充电过程以实现优化,但不能根据充电过程电池参数的动态变化做出优化调整。本文提出一种基于差分电压平台(DVP)的多阶恒流(DMCC)充电策略,将电池充电电压差分处理,并以差分电压平台区域为切换条件,在电池端电压达到切换条件后,以较上一阶段更低的电流值继续充电,重复该过程直到SOC 达到预设值。为获取电池的动态参数并进行优化,建立电-热-老化综合模型,以此为基础构建包括充电时间、充电效率和SOH 的多目标优化函数,利用改进的灰狼优化算法(GWO)求解各阶段优化电流,得到不同目标权重下的帕累托最优前沿。最后分析比较了VMCC、DMCC 和CC-CV 充电策略在充电时间、充电效率和循环寿命方面的充电性能。
1 电池模型
1.1 电模型
二阶RC 等效电路模型由于其简单高效且精度较高的特点,在电池研究领域被广泛应用。因此,本文选择采用二阶RC 等效电路模型来对锂离子电池进行建模,如图1 所示。图中:Uocv为电池开路电压,开路电压定义为电池在不受外部电流作用下的电压;Uk为电池端电压;R0为电池欧姆内阻;R1和R2为电池极化内阻,C1和C2为电池极化电容,用来描述电池充放电过程中电荷在电解质中的传递和储存现象[13]。

图1 二阶RC等效电路模型Fig.1 Second-order RC equivalent circuit model
模型参数关系可通过如下方程式表示:
电池的荷电状态SOC由安时积分法计算为:
式中,SOC(t0)为初始时刻电池的荷电状态;Cn为电池额定容量。
Uocv、R0、R1、R2、C1和C2是描述锂电池特性的参数,它们会随着电池的SOC 和温度的变化而变化[14]。因此,在进行电池模型仿真时,需要对这些参数进行辨识。混合脉冲功率特性实验(hybrid pulse power characterization,HPPC)可以通过施加脉冲信号,引发电池的动态响应,从而获取电池在不同SOC 和温度下的电压变化,进而进行参数辨识。如图2所示,在放电初始阶段,施加一个突增的脉冲电流信号,下降的这部分压降ΔU0由欧姆内阻R0引起;而在放电结束后产生的压降ΔU1,2由极化电容C1、C2和极化内阻R1、R2引起[15]。取充放电曲线的平均值作为电池的开路电压Uocv,SOCOCV特性曲线如图3所示。通过对相应阶段的电压曲线进行指数拟合,便可有效识别出R0、R1、R2、C1和C2,结果如图4所示。
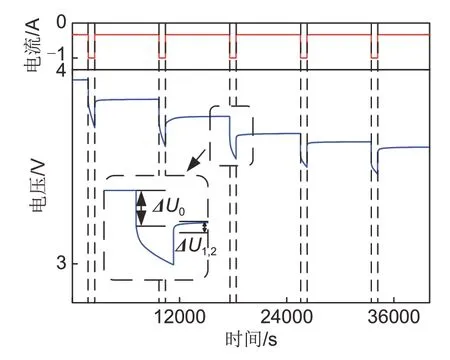
图2 HPPC实验Fig.2 HPPC experiment
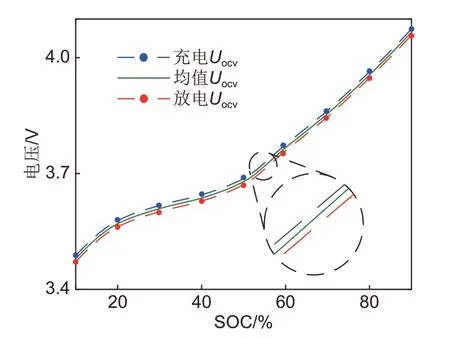
图3 SOC-OCV特性曲线Fig.3 SOC-OCV characteristic curve
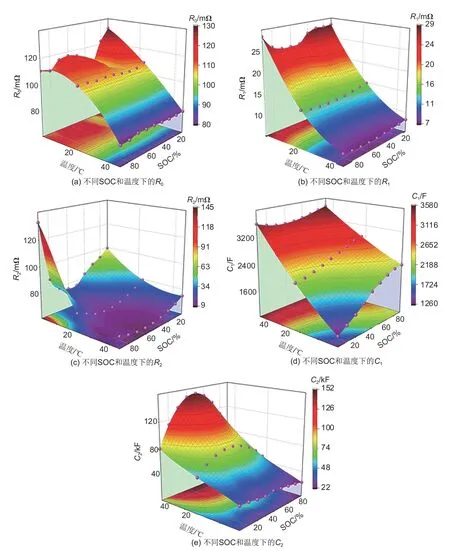
图4 不同SOC和温度下的R0、R1、R2、C1和C2Fig.4 R0, R1, R2, C1 and C2 at different SOCs and temperatures
1.2 热模型
若假设电池内部发热量分布均匀,并且电池比热容和传热系数为常数[16],则电池的发热功率可以用以下公式表示:
式中,Q0为电池总发热功率;Qj为电池内阻产生的焦耳热;Qr为电池内部产生的可逆热,这一部分的热功率描述了电池在充电过程中,由于内部锂离子在活性颗粒中脱嵌时伴随产生的活性颗粒晶体结构改变而引发的放热和吸热现象;Qe为热交换功率,用于反映电池与环境温度之间的热交换现象。电池总发热功率可表示如下:
式中,ch为电池的比热容;m为电池的质量;T为电池表面温度。
电池内阻产生的焦耳热可表示为:
由电池内部产生的可逆热如下式:
式中,∂Uocv/∂T表示电池开路电压随温度变化的温度系数,可以利用不同温度下的开路电压的差值与温度差的比值取平均值求得。
电池与环境温度之间的热交换功率可表示为:
式中,h为电池传热系数;S为电池表面积;Ta为电池环境温度。
综上可得到电池的温升模型:
1.3 老化模型
本文采用一种基于循环测试矩阵的老化模型[17]。基于测试结果可得到表征容量损失的半经验公式:
式中,Qloss为容量损失百分比;R为气体常数,其值为8.314 J/(mol·K);T为电池温度;Ah为电池从出厂到当前时刻的总放电容量;z为幂律因子,其值为0.55;B(C)为指前因子,表示为C倍率的非线性函数,见表1。

表1 不同充电电流倍率下的指前因子B(C)值Table 1 Pre-factor B(C) values at different charging current ratios
B(C)=-47.84C3+ 1215C2- 9419C+ 36040 (13)
电池的活化能Ea(C)与C倍率的关系式可表示如下:
一般认为,锂离子电池的容量损失达到20%时,电池寿命终止,即Qloss=20 时,电池的循环寿命耗尽[18]。因此,将Qloss=20 代入式(12)即可得到电池从出厂到寿命耗尽时的总放电容量[19]:
由于电池的一次循环包括充电和放电两个过程,而Atotal(C,T)仅表示放电过程,因此电池的总充电放电容量可近似表示为2Atotal(C,T)。单次充电过程电池的健康状态SOH可表示如下:
2 充电优化策略
2.1 自适应多阶段恒流充电策略
CC-CV 充电策略因其控制方法简单便捷、易于实现且成本较低,是目前应用最广泛的充电策略。然而,在整个充电过程中,优化变量仅限于恒流阶段的电流,控制方式不够灵活。仅仅提高恒流阶段的充电电流以追求更快的充电速度,可能会导致电池温度升高,从而加重电池老化,无法满足用户的需求。相比之下,多阶恒流(MCC)充电策略将恒流阶段分成多段,每个阶段采用不同的充电电流值,增加了优化空间,可根据电池充电状态动态调整充电电流值。可以更加灵活地控制充电电流,以最大限度地提高充电速度,同时避免电池温度升高过快,减轻电池老化的风险,从而更好地满足用户的需求。如图5所示,在充电初期,采用较大的电流对电池进行充电,以提高充电速度。当电池端电压达到设定的上限后,充电电流会被降低,以防止过充现象的发生。同时,随着充电电流的下降,电池端电压也会随之下降,直到趋于稳定后再继续上升。这个过程会不断重复,直到电池电量达到设定的阈值,从而完成充电过程。在充电过程中,充电电流呈逐阶段下降的趋势,这种机制有效抑制了电池温升的速度,从而降低了电池的老化程度。本文采用的电池型号为INR18650-20R,其额定容量为2000 mAh,充电截止电压为4.2 V。

图5 五阶段恒流充电曲线Fig.5 Five-stage constant current charging curve
2.2 优化目标
在电池充电优化过程中,电池的充电时间、充电效率、温升和循环寿命通常是最关键的评价指标。较高的充电速度可以缩短充电时间,提高充电效率,但会增加电池温度,从而加快老化速度,这些评价指标之间存在明显的矛盾。因此,在优化充电过程时,需要建立包含多目标的优化函数。根据式(16)可知,电池的健康状态(SOH)与温度(T)之间存在强烈的相关性,即SOH会随温度的变化而变化。因此,在本文的优化过程中,考虑充电时间、充电效率和SOH这3个因素。考虑到三者所对应的目标函数值存在较大差异,为便于权衡各目标,需对目标函数进行归一化处理。处理后的各目标函数可分别表示为:
式中,tend为充电结束时刻的时间;t0为充电开始时刻的时间;tmax为最大充电时间;ηtend为充电结束时刻的充电效率;ηmax为最大充电效率;ηmin为最小充电效率;SOHtend为充电结束时刻的电池健康状态;SOHmax为最大电池健康状态;SOHmin为最小电池健康状态。
对上述目标函数进行加权,可得到总目标函数:
式中,α、β和γ分别为充电时间、电池健康状态和充电效率的权重,权重值越大表示对应的优化目标越重要。
2.3 优化算法
为了获得最优的充电电流和相应的最佳适应度值,本文采用了一种改进的GWO算法作为迭代寻优的方法。针对传统的GWO算法容易陷入局部最优的问题,本文参考了文献[20]中的方法,对收敛因子进行非线性化处理,并引入了权重策略,以提高算法的性能。GWO 算法是一种基于自然界中灰狼行为的优化算法,通过模拟灰狼个体之间的社会行为和个体行为来进行优化搜索,从而在搜索空间中找到最优解。灰狼严格遵守社会等级关系,底层狼群听从顶层狼群指挥进行狩猎(寻优)行动。其中α、β和δ为算法迭代过程中的3个最优解,其他灰狼个体则需根据α、β和δ狼更新位置。个体更新迭代的过程如下式:
式中,Dα、Dβ和Dδ分别为灰狼个体与α、β和δ狼之间的距离;X1、X2和X3分别为灰狼个体向α、β和δ狼移动的趋势;A和C为系数向量,可表示为:
式中,r1和r2为[0,1]区间的随机向量;α为收敛因子,由于GWO算法寻优过程不是线性变化的,因此需对α进行非线性化处理,改进后可表示如下:
式中,t为当前迭代次数;T为最大迭代次数。改进后的收敛因子α在迭代初期减小速度变慢,这有利于狼群扩大搜索范围。而在迭代中期,收敛因子α的减小速度加快,这有利于狼群集中搜索猎物。这种非线性化处理的策略在GWO算法中起到了优化搜索性能的作用。
传统的GWO 算法在计算灰狼个体更新位置时没有充分考虑顶层α、β和δ狼的决策能力,容易陷入局部最优解。因此,可根据顶层α、β和δ狼的适应度值,计算相应的权重,并通过加权的方式利用式(24)来计算灰狼个体更新后的位置:
式中,ω1、ω2、ω3分别为α、β和δ狼的权重系数。这种引入权重的策略能够有效提升算法的全局搜索能力。
基于改进灰狼算法优化充电过程的包括以下步骤,流程如图6所示。

图6 GWO算法优化流程Fig.6 GWO algorithm optimization flowchart
步骤1:参数初始化。由于优化充电策略为五阶恒流充电策略,因此个体维度设置为5,狼群数量设置为30,最大迭代次数设置为200次;
步骤2:根据充电电流计算电池模型中的各参数值;
步骤3:根据式(21)和式(22)计算适应度值;
步骤4:根据式(31)迭代更新灰狼个体的位置,比较个体适应度值,得到全局最小值和全局最优位置。
步骤5:重复步骤3、4,直到达到最大迭代次数。
在每一代迭代中,根据灰狼个体之间的竞争和合作关系,更新每个灰狼个体的位置和适应度值。通过不断迭代更新,灰狼优化算法逐渐收敛到最优解,从而实现对优化问题的求解。
3 优化结果和讨论
本节将分别探讨以截止电压和差分电压平台(DVP)作为恒流切换条件,对充电优化效果的影响。在优化目标方面,将考虑充电时间、充电效率和电池健康状态,通过改变各目标权重值,生成优化策略。为确保充电优化模型的有效性和可行性,需对参数范围进行约束,具体情况见表2。在表中,值所在列表示模型中各项参数的优化限制范围,其中电流I、端电压Uk和温度T的取值参考了电池制造厂商提供的安全充电范围。初始SOC设定为10%,表示电池的电量非常低,需要进行充电操作;目标SOC 设定为90%,表示电池的电量接近满电,可以认为充电过程已经结束。为确保适应度值的准确计算,并实现充电优化目标的均衡求解,充电时间t、充电效率η和电池健康状态SOH 的优化取值范围基于仿真实验数据设定。

表2 优化约束和初始条件Table 2 Optimize constraints and initial conditions
3.1 VMCC充电优化策略
根据式(22)中的权重值约束,不同的权重值组合会得到不同的优化策略。为解决多目标优化问题中量纲不同、互相冲突的问题,采用帕累托最优前沿方法,该方法可以同时考虑多个优化目标,并以一种可视化的方式显示不同权重值下的优化策略,如图7所示。随着充电时间权重值的减小,优化充电策略在帕累托前沿上由策略1向策略4方向移动,这种反比例的三维界面移动趋势表明3个优化目标之间存在相互制约的关系。追求快速充电会导致电池老化加重且充电效率降低,不符合安全充电规范;而最小老化策略则会延长充电时间,显然这种策略无法满足用户需求。因此,可以在帕累托前沿曲线的拐点处寻找均衡充电策略。该区域的充电策略能够更好地平衡充电时间、充电效率和电池老化这3个优化目标,从而得到更为均衡的充电策略。

图7 三目标帕累托前沿Fig.7 Three goals Pareto frontier
为了选取最佳均衡充电策略,本研究比较了拐点区域的4 种充电策略,对应的权重值见表3。权重值的选择会影响优化目标的倾向程度。如图8所示,由于策略1中充电时间权重值较高,充电优化更加注重充电速度。因此,优化得到的最佳电流相对较大,有效减少了充电时间,整个充电过程仅持续2495 s。然而,与此同时,相应的效率和老化权重值会减小,导致效率的降低和老化的加重。策略4相较于其他策略更加注重充电效率和电池老化方面的优化。通过优化得到的最佳电流减小,进而使得电池端电压和温升降低。整个充电过程中,电池的SOH 仅衰减0.005583%,满足了低损充电的需求。然而,充电电流的减小也意味着要达到目标SOC需要更长的充电时间。图9比较了4种充电策略的充电时间,充电效率和循环寿命,与策略4相比,策略1 的充电时间减少了47.97%。然而,由于策略4更倾向于效率和老化,其最佳电流也偏向于小电流值。因此,在整个充电过程中,其最大温升仅为3.08 ℃。小电流及小温升的共同作用使得策略4 的老化减少了33.25%,充电效率增加了3.08%。

表3 4种充电策略的权重因子Table 3 Weight factors for the four charging strategies

图8 4种充电策略的电池状态变化Fig.8 Battery state changes for four charging strategies

图9 4种充电策略的充电时间、充电效率和循环寿命比较Fig.9 Comparison of charging time, charging efficiency and cycle life of four charging strategies
3.2 DMCC充电优化策略
本节将使用DVP 作为切换恒流充电的切换条件,以优化充电策略。采用策略4的第一阶段电流进行恒流充电,电池的端电压及差分充电电压(differential charging voltage,DCV)的变化趋势如图10(a)所示。其中,条形区域表明DCV曲线出现了平台现象。此时,电池的端电压不再增加,而是保持在一个相对稳定的电压水平上,电荷的输入无法进一步提高电池的端电压。这是因为电池负极上形成了固体电解质界面(SEI)膜和锂枝晶,阻碍了电荷的传输和储存,导致电池性能的衰退和容量的损失。因此,DCV 曲线出现平台可以用于检测电池的健康状况并判断是否发生了析锂现象。图10(b)显示了以DMCC 策略充电优化后的端电压及DCV变化。当DCV 达到平台时,调整充电电流可以抑制析锂的发生,从而减小电池老化程度。

图10 以恒流和DMCC策略充电时端电压及DCV变化Fig.10 Terminal voltage and DCV change when charging with constant current and DMCC strategies
为了验证本文提出的充电策略的优越性,以策略4的各目标权重值优化以得到对应的DMCC充电策略,同时进行了VMCC、DMCC 和0.5C-CCCV三种策略的比较分析。如图11 所示,DMCC 充电策略较VMCC充电策略更早达到恒流切换条件,其平均充电电流相对较小,从而产生的温升也较小,因此会产生更小的老化,将总适应度值减小了3.1%。与传统的0.5C-CCCV 充电策略相比,DMCC 策略在充电初期采用较大电流充电,提高了充电速度。从图12 的比较结果中可以看出,DMCC 策略处于较为均衡的位置,与0.5C-CCCV 策略相比,将充电时间缩短了10.46%,而增加的老化仅为0.99%,基本持平。
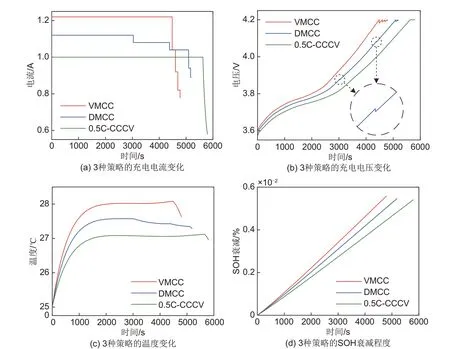
图11 3种充电策略的电池状态变化Fig.11 Battery state changes for the three charging strategies

图12 3种充电策略的充电时间、充电效率和循环寿命比较Fig.12 Comparison of charging time, charging efficiency and cycle life of three charging strategies
4 结 论
为平衡充电过程中充电时间、充电效率和SOH三个目标,以INR18650-20R锂离子电池为研究对象,建立了该电池的电-热-老化耦合模型,提出了一种基于改进GWO 算法的锂电池DMCC 充电策略,并与相同权重下的VMCC充电策略和传统0.5CCC-CV充电策略进行分析比较,得出以下结论。
(1)通过综合考虑充电时间、充电效率和SOH三个因素进行优化,得到的均衡充电策略能够更好地平衡充电过程中的各个参数,实现安全稳定的充电。
(2)改进的GWO算法在处理多目标优化问题时,具有全局搜索能力强、易于实现和收敛速度快的优点。通过结合帕累托最优前沿,可以根据不同场景和需求选择合适的充电策略。
(3)提出的DMCC 充电策略具备动态调整充电过程的能力,能够根据电池充电电压的变化进行灵活的优化求解。与VMCC策略相比,该策略能有效降低电池的老化程度,并将总体适应度值综合减少了3.1%。相对于0.5C-CCCV策略而言,该策略将充电时间缩短了10.46%。

