基于半监督判别分析的领域自适应方法研究∗
成佳骏 李 波
(1.武汉科技大学计算机科学与技术学院 武汉 430065)(2.武汉科技大学智能信息处理与实时工业系统湖北省重点实验室 武汉 430065)
1 引言
在计算机视觉领域中,许多机器学习方法被用来做图像分类任务。比如,线性回归[1]、逻辑回归[2]、k近邻[3]、决策树[4]、支持向量机[5]。但是,当图像特征表示过于冗余或质量较差时,其准确性将降低。因此,提取高质量图像特征非常重要。
特征提取是作为挖掘图像潜在特征的一种重要方式,不仅有利于对图像内容的深入理解,而且对于提高图像分类和识别的准确率也至关重要。有许多经典的特征提取方法。比如,主成分分析(Principal Component Analysis,PCA)[6]、独立成分分析(Independent Component Analysis,ICA)[7]、线性判 别 分 析(Linear Discriminant Analysis,LDA)[8]等。以上的算法是全局的,无法从中提取局部流形结构信息。为了发现隐藏在高维数据中的非线性结构并挖掘数据的局部几何结构信息。拉普拉斯特征映射(Laplacian Eigen-maps,LE)[9]、局部线性嵌入(Locality Linear Embedding,LLE)[10]和其他流形学习算法也被提出用于特征提取。此外,深度学习方法也应用于特征提取[11~12]。
然而,以上提出的算法通常需要大量与测试(目标域)样本具有相同分布的训练(源域)样本,并且当标记的训练样本不足且具有分布偏差时,算法性能将会受到很大影响。领域自适应(Domain Adaption)问题解决了源域和目标域之间的样本分布不一致的问题。如何有效地衡量域之间分布差异是领域自适应的关键步骤。常用的方法包括基于熵的KL 散度[13]、Bregman 散度[14]、最大均值差异(Maximum Mean Discrepancy,MMD)[15]。Zhuang等[16]通过将KL散度作为域间分布自适应提取深度特征,提出一种自编码的领域自适应方法。Si等[17]将Bregman 差异添加到子空间学习的目标函数中,提出了转移子空间学习(Transfer Subspace Learning,TSL)方法。然而,需要密度估计的流程阻碍了KL 和Bregman 散度的适用性。之后,香港大学的Pan等提出迁移成分分析(Transfer Component Analysis,TCA)[18],使用MMD 消除了再生核希尔伯特空间(Reproducing Kernel Hilbert Space,RKHS)中域之间分布差异,减少源域和目标域间的边缘分布差异。龙明盛等提出了迁移联合匹配方法(Transfer Joint Matching,TJM)[19],在优化目标中同时进行边缘分布自适应和源域样本选择。随后,龙明盛等提出的联合分布自适应方法(Joint Distribution Adaptation,JDA)[20]的目标是同时减少源域和目标域的边缘分布差异和条件分布差异。王晋东等提出平衡分布自适应(Balanced Distribution Adaptation,BDA)[21]方法来解决JDA 中忽略边缘分布和条件分布优先考虑的问题,该方法能够根据特定的数据领域,自适应地调整分布适配过程中边缘分布和条件分布的重要性。
虽然基于MMD 的领域自适应方法很方便,但是有必要构建一个与样本大小成正比的分布差异矩阵,增加了计算成本。另外,这些方法都没有考虑到源域和目标域样本的标签信息,没有保留投影到子空间后样本数据的流形结构。许多机器学习研究人员发现,未标记数据与少量标记数据结合使用时,可以大大提高学习准确性[22]。因此,基于LDA[8]的半监督判别分析(Semi-supervised Discriminant Analysis,SDA)[23]被提出。SDA 的目的是找到一个投影矩阵W,该投影从标记的数据点推断出判别结构,以及从标记和未标记的数据点推断出固有的几何结构。
为此,本文提出一种基于半监督判别分析和跨域均值差异(Semi-supervised Discriminant Analysis And Cross-domain Mean Measure,SDA-CDMD)的领域自适应方法。首先,用源域和目标域到彼此域均值距离的平方和表示两个域之间的差异(CDMD)。其次,将SDA 加入到优化目标,保证数据映射到子空间后的局部几何信息。最后,通过最小化CDMD 并结和SDA 来构造关于投影矩阵W 的目标函数。减少域之间的边缘分布差异和条件分布差异,促进域之间的知识迁移。与基于KL 散度、Bregman 散度和MMD 的领域自适应算法相比,基于SDA-CDMD 的方法具有计算成本低,所需内存少,知识传递效率高,易于推广和应用的优点。
2 半监督判别分析
半监督判别分析(Semi-supervised Discriminant Analysis,SDA)[23]的目标是学习一个全局的投影变换,使其不仅具有较好的分类判别能力,同时保持数据的局部分布特性。假设样本数据集X=XS∪XT=[x1,x2,…,xN]∈Rd×N,其中N=n+m。SDA 的目标函数如下所示:
其中,WTXLXTW 是一个正则项。a 是全局散度与正则项之间的平衡参数。正则项的拉普拉斯矩阵为L=D-S。其中,S 表示由X 组成的邻接矩阵。在本文中,矩阵S定义为
D是一个对角矩阵:其条目是S的列(或行)的总和,表示如下:
Sb和St分别表示样本X的类间散度矩阵和全局散度矩阵,具体定义如下所示:
Sw表示X 的类内散度矩阵,N(c)和u(c)分别表示X 中包含c类样本的数量和平均值。由于目标域是没有标签的,所以在标签迭代过程中用伪标签替代。每次迭代后都需要更新目标域标签。在式(4)和式(6)中,u 表示样本数量为n+m 的X 样本均值。如下所示:
本文中,X 由源域样本和目标域样本组成,n和m分别为源域样本数量和目标域样本数量。
3 跨域均值差异
为了衡量两个域之间的分布差异,本文提出了一种新的域之间度量准则:跨域均值差异(Corss-Domain Mean Discrepancy,CDMD)。
假设源域Ds和目标域Dt的样本数量固定,CDMD通过两个域之间到彼此域样本均值点欧式距离的平方和来评估Ds和Dt的分布差异。如图1 所示,在源域和目标域的原样本空间中分别有三类样本点及其均值:xS(1),xS(2),xS(3),uS和xT(1),xT(2),xT(3),uT。从xS(1),xS(2),xS(3)到uT的距离分别为dS(1),dS(2),dS(3)。而从xT(1),xT(2),xT(3)到uS的距离分别为dT(1),dT(2),dT(3)。可以用下式表示这两域之间的分布差异。
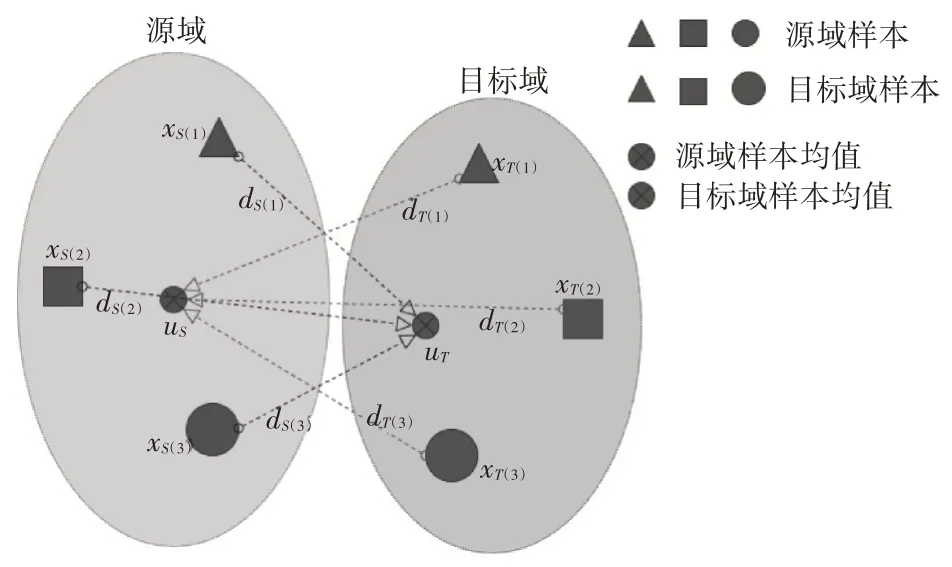
图1 原始样本空间
因此,通过CDMD计算Ds和Dt之间的分布差异公式为
图1和式(9)表明,当样本数量保持不变时,d2(Ds,Dt)越小,源域样本点越接近目标域样本均值点;目标域原本点越接近源域样本均值点,域之间的分布差异越小。
为了提取最佳的共享特征表示,本节通过学习一个基于CDMD 的最优特征子空间的投影矩阵W。如图2 所示,通过投影变换zS=WTxS和zT=WTxT,投影后源域和目标域样本点及其均值变为zS(1),zS(2),zS(3),ûS和zT(1),zT(2),zT(3),ûT。从zS(1),zS(2),zS(3)到ûT的距离分别为d̂S(1),d̂S(2),d̂S(3)。从zT(1),zT(2),zT(3)到ûS的距离分别为d̂T(1),d̂T(2),d̂T(3)。本章希望找到一个映射矩阵W使得式(11)成立,进而减少域之间的分布差异。
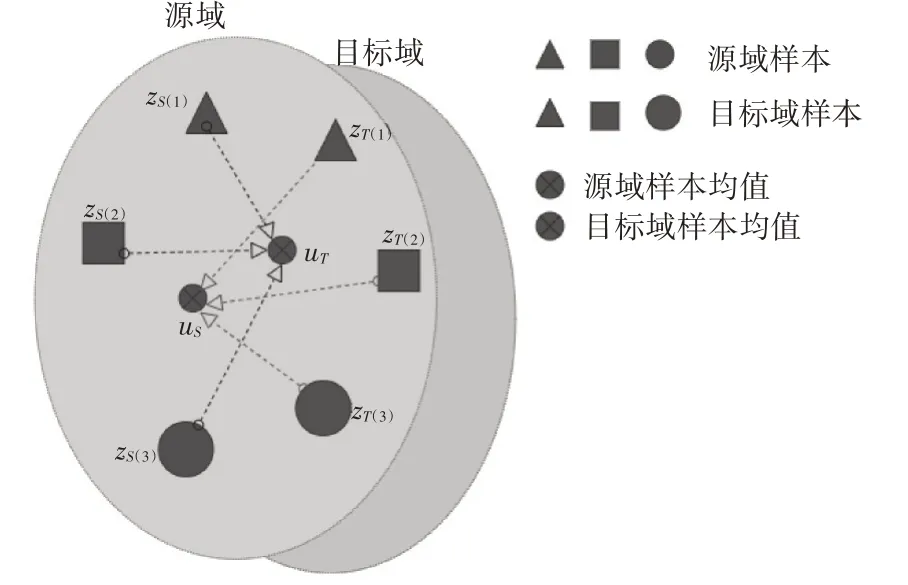
图2 投影后样本空间
因此,为了找到最佳的共享特征子空间,通过将低维投影矩阵W 加入到式(9)中,可以得到基于CDMD的优化目标函数如下所示:
其中,u 由式(10)表示,式(13)写成矩阵形式如下所示:
4 SDA-CDMD算法
在SDA-CDMD 方法中,给定有标签的源域数据集Xs={(x1,y1),(x2,y2),…,(xn,yn)}∈Rd×n和没有标签的目标域数据集XT={x1,x2,…,xm}∈Rd×m。其中n 和m 分别是源域样本和目标域样本数量,d 是原始特征空间维度。
4.1 目标函数
SDA-CDMD 算法将SDA 与CDMD 相结合构造出关于投影矩阵W的优化目标函数。另外,在目标函数上添加经典领域自适应方法TCA[18]和JDA[20]使用的正则化项。最终的目标函数为
其中,M=XXT-XuT-XTu+uuT。||W||2 F 是投影矩阵的稀疏约束项,l是平衡参数,||·||2 F是矩阵F-范数的平方运算。参数b 用于权衡SDA 与CDMD 之间的权重。
优化问题(14)的求解可以转换为拉格朗日乘数法求解广义特征值的问题。定义L=diag(l1,l1,…,lk)为拉格朗日乘子,式(14)的广义特征分解为
求解等式(15)得到的前k 个最大特征值对应的特征向量组成的矩阵即为投影矩阵W。
4.2 算法流程
在上述理论的基础上,本文提出的SDA-CDMD算法步骤见算法1。
算法1 基于SDA-CDMD领域自适应算法步骤
输入:源域样本XS和目标域样本XT,子空间维度k,参数a、b、l,最大迭代次数T。
输出:投影矩阵W
1)直接训练源域样本得到一个分类器f,通过f 得到目标域样本的伪标签。初始化矩阵St和Sb。
2)令跌代次数t=1;
3)求解式(15)得到投影矩阵W;
4)由W得到低维数据ZS=WTXS和ZT=WTXT;
5)用{ZS,YS}训练出一个分类器f,通过f 得到目标域样本的伪标签。更新矩阵St和Sb;
6)t=t+1;
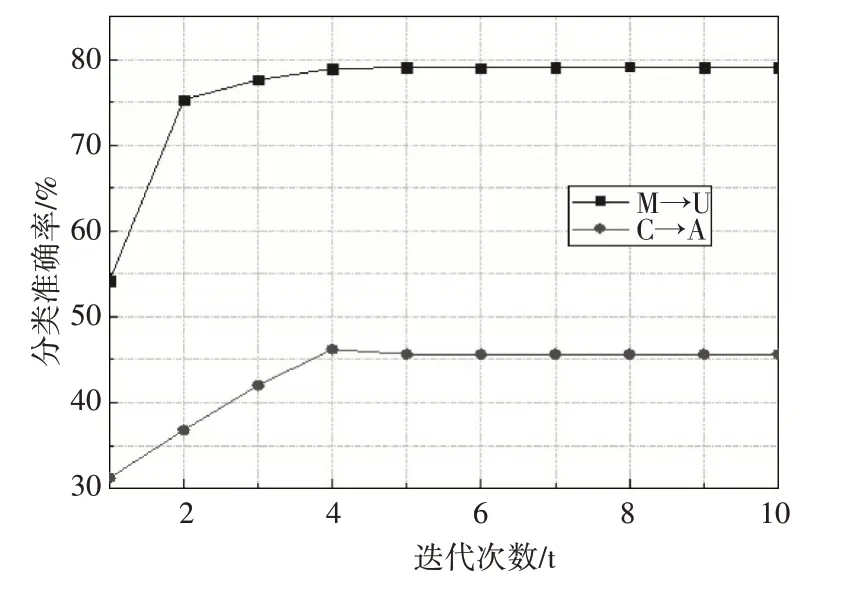
7)如果t 为了对本文提出的方法进行验证,将本文提出的SDA-CDMD 算法与传统的领域自适应算法进行实验结果比较,比较的方法包括GFK[24],TCA[18],TSL[17],JDA[20],TJM[19],BDA[21]。以此对本文所提出算法的有效性和实用性进行评估。 USPS 数据集和MINST 数据集都是手写数据集,具有手写的数字0-9 的十个类别。它们的分布不同但是联系紧密,都具有手写的数字0-9 的十个类别。在实验中,构建两组实验数据作为域适应问题:U→M(USPS 作为源域,MINST 作为目标域)和M→U(MINST作为源域,USPS作为目标域)。 Office+Caltech 数据集由Gong 等第一次被提出[25],它包含Office和Caltech两个数据集。有四个域C(Caltech),A(Amazon),W(Webcam)和D(DSLR)。在实验过程中,两个不同的域随机选取分别作为源域和目标域,比如C→A(Caltech 作为源域,Amazon 作为目标域)。一共有12 种域适应问题。 在对比实验中,设置本文算法的参数:子空间维度k=100,正则项系数a=0.001,最大迭代次数T=10。另外在USPS+MNIST 数据集上设置平衡参数b=1,正则项系数l=0.1。在Office+Caltech 数据集上设置b=0.5,l=1。其它方法的参数使用它们各自文献的最优参数,选用k-NN 分类器对USPS+MNIST数据集的两组域适应问题(U→M,M→U)和Office+Caltech 数据集的9 组域适应问题(C→A,C→W,…)使用7种领域自适应方法进行比较,比较结果如表1和表2所示。 表1 USPS+MNIST数据集分类准确率(%) 表2 Office+Caltech数据集分类准确率(%) 从表1和表2的结果分析中我们可以得出以下两点结论: 第一,BDA、JDA、SDA-CDMD 这些共享特征提取算法的准确率总体上高于TCA、GFK 和TSL。表明同时减少两个域之间的边缘分布差异和条件分布差异,更有利于对齐源域与目标域,保留数据的本质属性。 第二,SDA-CDMD 的平均准确率总体上优于其它几种传统的领域自适应算法,这就表明SDA-CDMD 在特征提取过程中充分利用了标签信息使得类内散度最小化,类间散度最大化,这样可以充分挖掘数据的局部几何结构信息。在投影到子空间后保留了样本的原始几何结构,同时通过CDMD减少了域之间的分布差异。 根据目标函数(14),SDA-CDMD 算法性能受参数a、b、l 和子空间维度k 的影响。因此,为了测试SDA-CDMD 对参数的敏感性并研究其随着迭代次数的增加算法的收敛性。我们分别选取USPS+MNIST 数据集的M→U 域适应问题和Office+Caltech 数据集的C→A 域适应问题。对这两组实验采用控制变量法找到每个最优的参数结果,图3分别展示了给定其他三个参数值,变换剩余一个参数值时分类准确率的变化趋势。 图3 参数设置 另外,记录这两组实验在每次迭代后的分类准确率,如图4所示。 图4 迭代次数分类准确率 通过图3 和图4 可以看出:1)随着迭代次数的增加SDA-CDMD 的精度在4 次迭代后逐渐增强并稳定下来,这说明算法具有很强的收敛性能。2)SDA-CDMD 的精度随着子空间维度的增加而提高,然后基本保持不变。3)正则化参数a的变化导致分类准确率的波动较大,并且两组实验的趋势不同。总体来说两组实验在区间a∈[0.0001,0.01]效果最好。4)平衡参数b 在区间[0.5,1]中,两组实验的分类准确率最高。5)随着正则化参数λ的增加,两组实验的分类准确率先升再降。M→U 实验在λ=0.1 处取得最优值,C→A 实验在λ=1 处取得最优值。 本文提出的基于半监督判别分析和跨域均值差异的领域自适应(SDA-CDMD)方法,通过三方面实现领域自适应:1)将源域和目标域映射到同一子空间,减少两个域之间的边缘分布差异和条件分布差异;2)利用半监督判别分析方法使数据在投影后保持原有的几何结构信息,同时使得同类样本更聚集、异类样本更分散;3)为了有效衡量域之间的分布差异同时提高计算效率,提出一种跨域均值差异的度量准则。在多个数据集上的对比实验可以看出,SDA-CDMD 算法效果总体上优于其它传统的领域自适应方法。 本文算法虽然相较于一些传统算法有一定的改进,但仍有不足之处。如本文算法中分类器仅选用k-NN,后续将尝试不同的分类方法来提高分类准确率。近年来,随着深度学习的发展,各种深度学习模型不断提出,后续会考虑将本文算法和深度学习相结合。5 实验与数据分析
5.1 数据集描述
5.2 方法比较


5.3 参数设置及收敛性分析

6 结语

