剪叉式升降台设计及结构优化
马向南
(中国南方电网超高压输电公司昆明局,云南 昆明 650217)
剪叉式升降平台具有结构简单、举升力大、可靠性高、通用性强等特点,举升过程中可以保持较好的平稳性,被广泛应用于现代物流、工业生产、设备安装与维护等领域[1-2]。
合理地设计剪叉臂的连接位置及优化机械臂结构对改善剪叉装置的工作压力、设备的轻量化设计有至关重要的作用。文献[3]利用有限元分析软件ANSYS Workbench建立了升降平台的有限元模型,对其在平台升、降以及台板合、张4种工作状态下的静态承载性能进行了仿真分析,为剪叉升降平台的力学性能分析提供了参考;文献[4]分析了升降平台的静强度,并利用ANSYS软件的优化模块对剪叉臂进行结构尺寸优化,从而减轻了剪叉臂质量;文献[5]基于响应面法对剪叉式升降平台进行结构优化,使液压缸的最大推力和整体最大应力均有所降低。传统剪叉式升降台的设计方法为经验设计法,即仅仅依靠经验拟定几组参数,分别进行数值分析,然后选取最优的参数组,这难以确保最终的方案为最优解。而响应曲面法(response surface methodology)是利用统计学综合实验技术解决复杂系统输入与响应关系的一种方法,基于样本点估计整个设计空间的变化规律,不必进行有限元求解,通过响应面就能得到输出函数值,大大减少了计算量,同时使用合理的优化算法,使各个子目标函数均能逼近全局最优解[6-7]。
本文设计了一种三级剪叉式升降台,为保障作业过程中剪叉装置能满足需求以及保障人员安全,对剪叉进行静力分析,在确保剪叉臂强度的前提下对其进行形状优化,建立剪叉平台遗传算法优化模型,通过遗传算法对剪叉装置进行优化,从而减小最大应力并改善应力分布,提高设备的安全性能及使用寿命。
1 剪叉式升降台有限元模型
1.1 剪叉式升降台结构
剪叉式升降台主要由底盘、剪叉内臂、剪叉外臂、液压缸、工作平台、辅助连接件等部件组成,为中心对称结构。其工作平台最小高度为4.2 m,最大高度为8.9 m,工作平台尺寸为5.0 m×2.5 m,额定承载质量为1 000 kg,其结构如图1所示。各剪叉臂通过销轴连接,最底层和最高层的剪叉臂通过滑块与底盘和工作平台连接,升降台由变幅液压缸驱动臂体实现升降[8-9]。

1—设备;2—机械臂装置;3—剪叉升降平台;4—地面;5—机器小车;6—转动装置
1.2 参数化有限元模型
剪叉材料为Q345低合金钢,在HyperMesh软件中采用焊接及梁单元的方式对剪叉装置连接部分进行连接,并根据剪叉装置结构特点及实际形状,把各个剪叉臂划分成壳单元并赋予其属性,以达到较高的计算精度。此外,由于本模型优化的重点在于剪叉臂部分,因此忽略剪叉支座、液压缸、底盘、工作平台等部件。剪叉的载荷为作用在工作平台上的质量为1 000 kg的外部载荷,为模拟其所受外部载荷情况,在HyperMesh软件中通过刚性单元REB3将力Fq连接到骨架相应位置,所建立的有限元模型如图2所示。
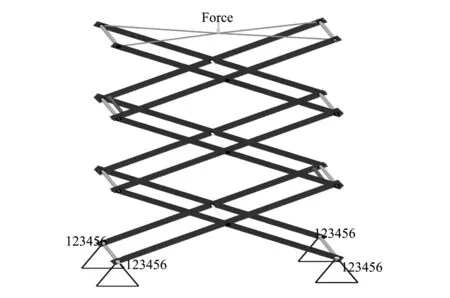
图2 剪叉有限元模型
对剪叉底部进行多点约束,约束所在的坐标系和剪叉为同一坐标系,图2中1、2、3分别为X轴、Y轴、Z轴的平动自由度,4、5、6分别为X轴、Y轴、Z轴的转动自由度。本文仿真分析是假设剪叉固定在地面上,因此6个自由度全部被约束。
2 实验设计
2.1 设计变量参数化建模
基于HyperMesh软件中的Shape功能,对所有剪叉臂进行形状设计变量参数化建模,对于空心矩形形状的剪叉臂结构,设计变量参数为其截面高度h、宽度b和型材厚度t,如图3所示。同时将连接两端剪叉臂的轴的厚度t2以及液压支撑杆的厚度t3设为尺寸变量。最终确定h、b为形状设计变量,t、t2、t3为厚度尺寸变量,一共5组设计变量。
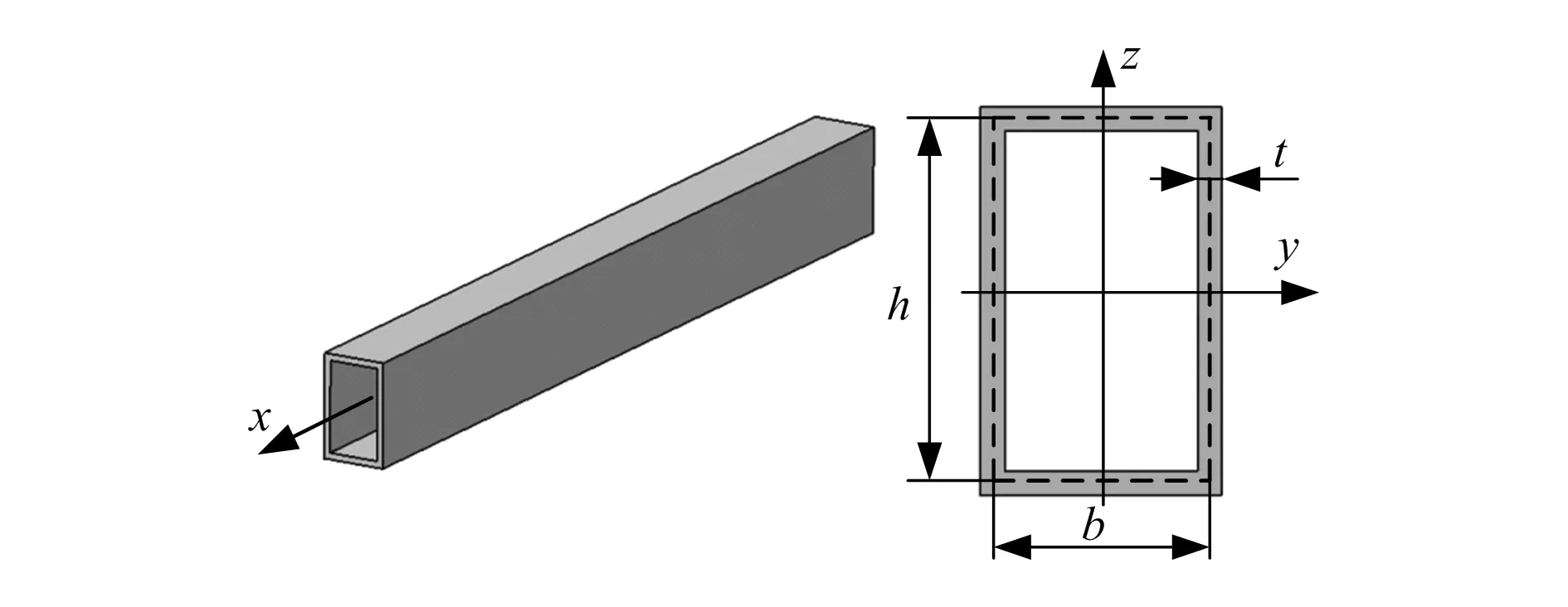
图3 剪叉臂截面及其局部坐标系
参数化建模时对剪叉臂组件的中性面网格按高度进行了20 mm的拉伸和压缩操作,按宽度进行了20 mm的拉伸操作,厚度变量的上下限分别为初始值的50%。参数化建模完成后的各组件参数的变化范围见表1。

表1 设计变量初始值及设计域
2.2 输出响应的设定
以有限元分析结果为基础,选择剪叉总质量,因变形而产生的最大变形、最大应力作为表征剪叉性能的评价指标,用作实验设计输出响应及优化设计的目标和约束,其基本信息见表2。

表2 输出响应性能指标的基本参数
2.3 实验设计采样
本文在HyperStudy中进行实验设计采样,提取剪叉装置有限元模型设计变量与性能响应的实验样本,可以采用的方法有拉丁超立方(Latin hypercube)法、哈默斯雷(Hammersley)法等。拉丁超立方法既能适应响应面为高度非线性的情况,又能保证样本点覆盖整个变量空间,因此实验使用拉丁超立方法来构造采样规模N=24的样本空间,并对各样本进行有限元求解。
3 响应面拟合
基于实验设计所采样的数据,本文采用最小二乘法(LSM)和径向基神经网络(RBFNN)法拟合模型,建立剪叉设计变量与性能指标之间的关系。
3.1 最小二乘法拟合
最小二乘法是一种用来获取一组独立的设计变量与系统输出响应之间某种近似关系的数学方法[10]。通过实验设计所采集的样本点,在HyperStudy中利用逐步回归的方法求得未知系数矩阵。为节省构建代理模型所需时间,只保留具有显著影响的回归项,建立多项式表达式如下:
D=101.569-11.218t-1.360t2-18.744h
(1)
F=659.231-203.955t-29.225b+20.259t2
(2)
M=0.040 1+0.172t+0.030t2+0.006t3+7.401×10-6h-1.306×10-5b+0.033th+0.033tb
(3)
3.2 径向基神经网络拟合
采用径向基神经网络得到3个性能响应与2个设计变量之间的关系如图4所示,图中所示是剪叉臂截面高度h和剪叉臂截面宽度b与各性能响应的3D等势面。对比各个3D等势面可以看出,位移和质量性能响应的非线性程度较高,质量响应的等势面比较线性,与实际情况相符。

图4 代理模型响应与设计变量关系图
3.3 拟合精度分析
本文采用统计学方法中决定系数R2(R-square)、绝对偏差均值比(relative average absolute error,RAAE)、均方根误差(root mean square error,RMSE)等误差评价指标,对模型预测值与仿真值之间的误差进行评价[10]。
1)决定系数表征代理模型与有限元模型的逼近程度,误差越大,R2的值越小,其定义为:
(4)
2)绝对偏差均值比是平均绝对误差与标准偏差之比,比值越低越好,其定义为:
(5)
3)均方根误差表示近似值与真实值之间的差异程度,是一种衡量加权平均误差的方法,精度越高均方根误差值越低,其定义为:
(6)
LSM和RBFNN拟合方法的精度对比见表3。

表3 LSM和RBF模型的精度比较
由表3可以得出:LSM方法拟合的M(剪叉总质量)响应精度更高;RBFNN方法拟合的F(最大应力)、D(最大变形)响应精度更高。
4 数学模型优化
4.1 目标函数和约束条件
优化目标是在减轻剪叉质量的同时,有效减少剪叉的工作压力,提高设备的安全性及使用寿命,因此将整个剪叉的质量作为优化目标。将剪叉起升过程中产生的最大位移和最大应力作为约束条件,使优化后所产生的变形值和应力值分别小于优化前,具体见表4。优化模型为:
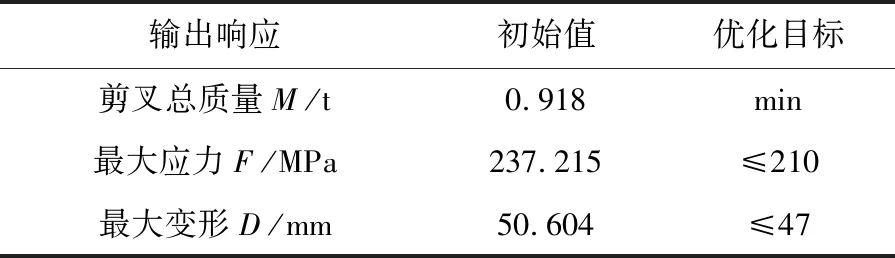
表4 响应初始值及优化目标
minM(x)=F1(x)
(7)
X=[Dtt2t3hbF]T
式中:F1=minM,t。
4.2 剪叉装置优化结果
基于Hyperstudy对剪叉模型进行优化,本文对质量响应采用拉丁超立方法拟合,对最大位移和最大应力采用径向基神经网络拟合,采用遗传算法(GA)进行优化[11-13]。基于GA对其进行迭代寻优,以寻求目标的最优解,同时也获得设计变量的解集[14]。在满足各个约束条件后,通过GA进行了迭代计算,得到40组解,其中包含1组违规解、38组可行解和1组最优解。各设计变量及响应优化前后的数值见表5。

表5 剪叉装置参数优化前后对比
从表5可以看出,基于响应面法对设计参数进行优化,剪叉的最大应力减小26.187 MPa,减小了11.04%;最大变形减小3.369 mm,减小了6.65%;剪叉质量减小0.037 t,减重率为4.03%。剪叉的工作压力明显减小,设备安全性能有较大幅度的提升。
5 优化前后性能对比及误差分析
5.1 优化前剪叉装置变形及强度分析
本文所采用的剪叉装置优化前的变形及强度如图5所示,由图5(a)可以看到,在剪叉平台施加1 000 kg载荷时,最大变形位于最上面第三阶剪叉臂位置,最大变形为50.604 mm,显然偏大。由图5(b)可以看到,最大应力值为237.215 MPa,主要集中在各个剪叉臂的连接位置,所用钢型材的结构安全系数为1.3~1.8,因此有较大的优化空间。

图5 优化前剪叉装置变形及强度
5.2 优化后剪叉装置变形及强度分析
优化后的变形及强度如图6所示,由图6(a)可看到,优化后变形产生的位移减小至47.27 mm;由图6(b)可知,优化后最大应力值为226.46 MPa。由此可知,本文优化结果使剪叉装置的综合性能得到了有效提升。优化前后剪叉装置位移最大的位置基本上都集中在各个剪叉臂最外端位置,因此要注重对各个剪叉臂的设计。
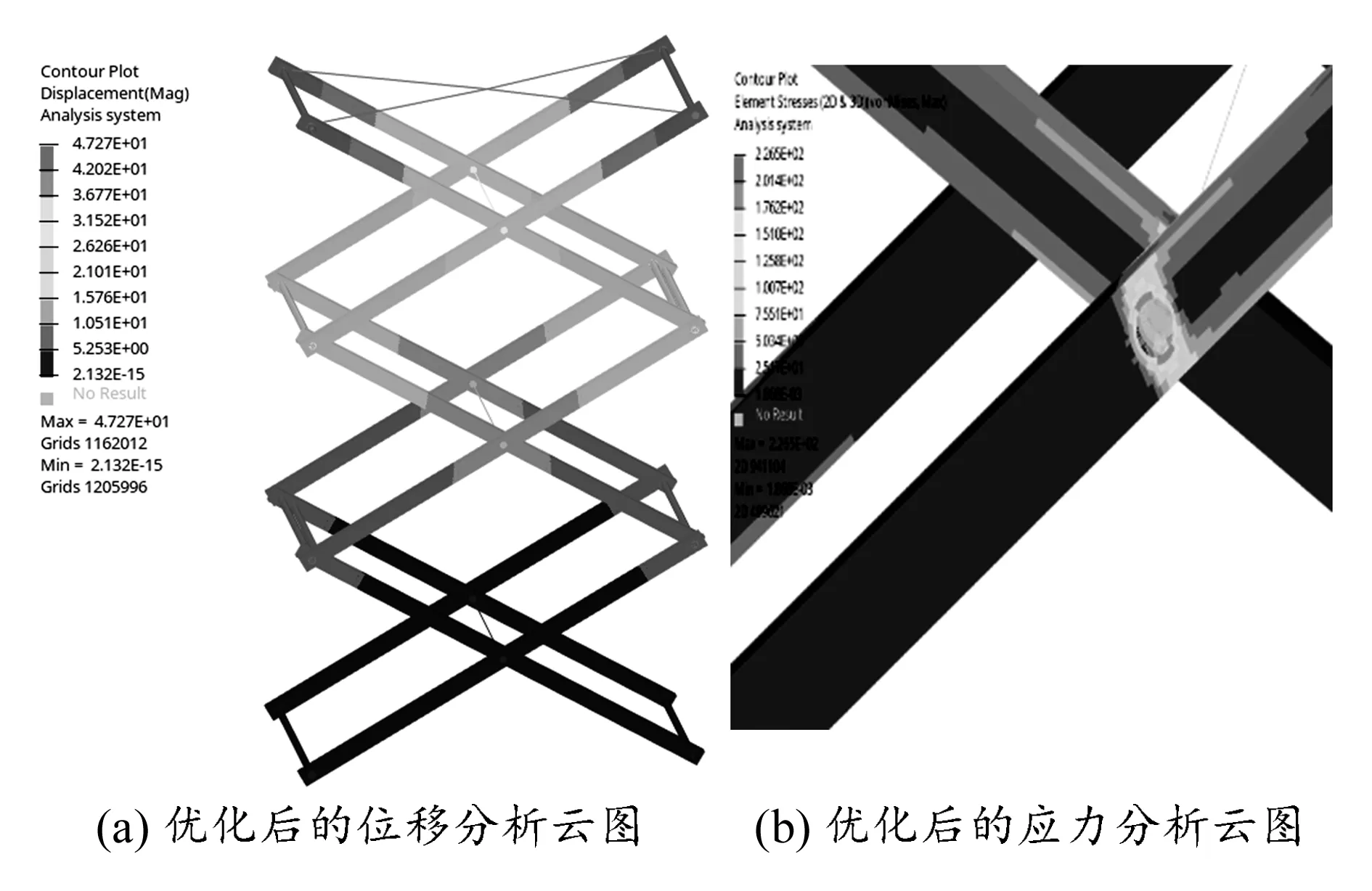
图6 优化后剪叉装置变形及强度
5.3 优化结果的误差分析
对优化后各项输出响应的有限元仿真值与代理模型的预测值进行相对误差分析,结果见表6。

表6 有限元仿真值与代理模型预测值的相对误差
6 结束语
本文设计了一种三级剪叉式升降台并以剪叉臂截面高度和宽度以及型材的厚度等作为设计变量对剪叉臂进行了优化。以剪叉质量为优化目标,以最大变形和最大应力为约束条件,基于响应面法构建代理模型,使用遗传算法完成剪叉装置优化,优化后的剪叉综合性能得到了有效提升。本文只针对剪叉装置进行了优化设计,以后还可从剪叉升降台关键部件入手,对升降台整体进行形状和尺寸优化,进一步提升优化效果。

