机械臂抓取避障路径修正虚拟仿真研究
赵启鹏
(枣庄市科技信息研究所,山东 枣庄 277800)
随着科学技术不断进步,机器人可以完成人类难以完成的工作。机械臂是机器人设计领域中较为重要的一项,能对困难、繁重的抓取工作提供极大帮助,工作内容包括货物分拣、电路安装、汽车装配等,可极大程度提升工作效率,降低用工成本[1-2]。近年来,随着生产技术的提升以及设备成本的降低,机械臂逐渐走入平常百姓的日常生活中,机械臂能够完美代替人力工作,实现拟人服务[3]。目前除了餐厅,大型图书馆也广泛应用机械臂服务读者,按照规划好的路线将读者归还的书籍抓取放置到合理位置;救援环境中安保人员也可以使用机械臂拆除危险物品。机械臂工作时会按照预先设定的轨迹工作,但是这种运行方式存在缺陷,导致机械臂不能在环境比较复杂的空间自如运作。实际工作中,需要稳定控制才能实现机械臂的稳定运行,所以合理规划机械臂的运行路径,是实现机械臂高效工作的手段之一[4-6]。合理规划机械臂的工作避障路径,能够使得机械臂在整个工作过程中始终保持无碰撞状态,沿着最佳路径工作。较为良好的路径规划能够保证机械臂在工作空间合理躲避障碍物,提升各个工作环节的结合度与配合度,提高机械臂的工作效率。
本文研究了机械臂抓取避障路径修正方法,在人工势场法基础上引入优化方法,提升机械臂路径避障优化效果。
1 基于改进人工势场法的机械臂抓取避障路径修正
1.1 机械臂运动学模型构建
使用沧州伟鹏机器人科技有限公司生产的GSK-RH06A3高精度机械臂作为本文避障路径修正研究对象,该机械臂属于经典6自由度机械臂,结构如图1所示。
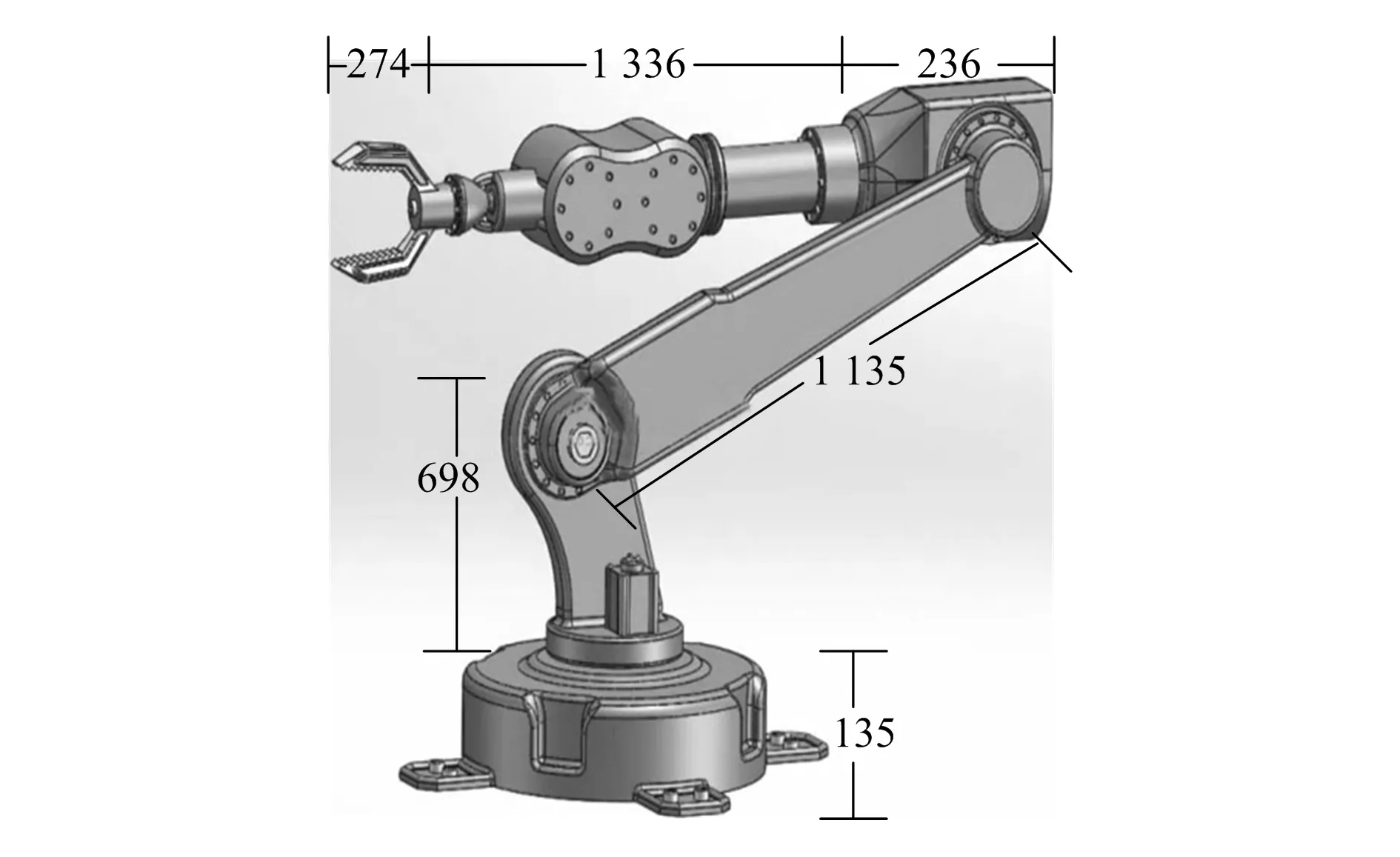
图1 机械臂结构
分析机械臂的运动学原理时,需要抓取机械臂末端结构的位姿[7],所以研究过程中需要利用Denavit-Hartenberg(D-H)方法构建机械臂各个连接杆的笛卡尔坐标系。本文所研究的机械臂是一个经典6自由度机械臂,各个机械关节在运行工作中都会与周围障碍物发生碰撞。为降低计算的复杂程度,需要抽象化绘制机械臂的各个结构[8-9]。把整个机械臂看作是一个刚性连杆,主臂与从臂是开链式多连杆机构。使用D-H法,结合机械臂的运动参数,绘制机械臂坐标系,如图2所示。

图2 机械臂坐标系
在机械臂的D-H参数中,通过4个参数描述机械臂各个连接部件之间的位置关系,设αi-1为关节夹角,由连杆属性决定该常量;θi为第i个自由度,即关节角;di和ai-1分别为连杆偏置距离和连杆长度,ai-1是常量。机械臂的D-H参数见表1。

表1 D-H参数
1.2 基于改进人工势场法的机械臂避障修正流程
机械臂θi邻近的空间即为人工势场算法的搜索空间,设该空间为(θi-λ,θi,θi+λ),其中λ为搜索步长,θi-λ、θi+λ分别是关节角θi逆时针和顺时针旋转λ后的角度。机械臂存在6个自由度,在抓取过程中,各个关节均有3种不同的取值,所以计算过程中遍历搜索空间(θi-λ,θi,θi+λ)的机械臂结构类型存在36种。根据机械臂整体综合势能确定和势场,通过与36种机械臂结构类型的和势场的比较确定和势场关节角组合为无碰撞避障修正路径,此时的关节角组合也是机械臂下一步移动路径。循环获取移动路径,机械臂不断向和势场降低速度最快的方向移动,最终进入目标范围。如果这一过程中路径陷入局部极值,则引入A*算法重新搜索最优解,跳出局部极值。确定跳出局部极值后,使用人工势场法搜索最优避障修正路径。机械臂避障修正路径流程如图3所示。
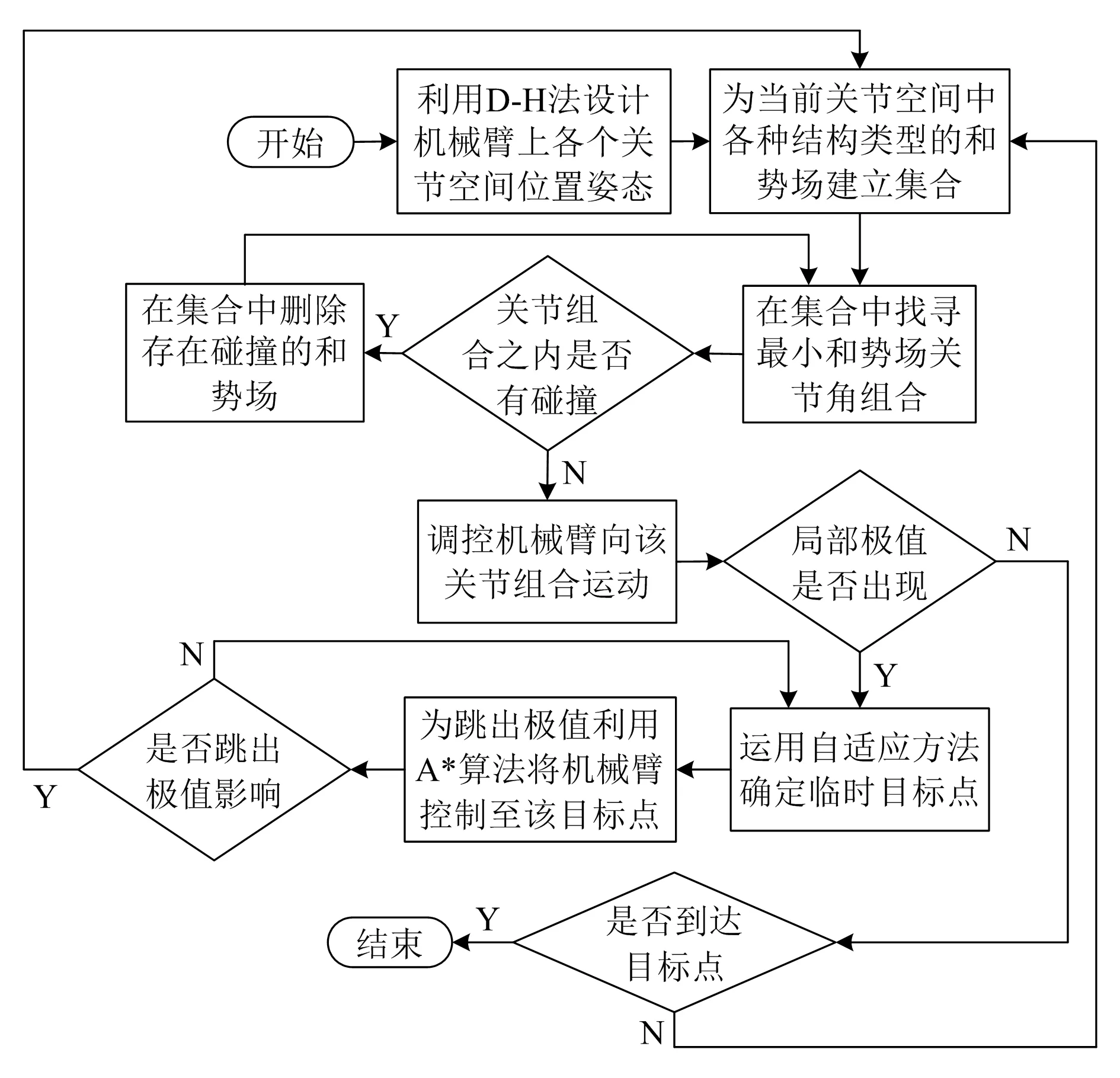
图3 机械臂避障修正路径流程
当人工势场法控制机械臂陷入极值时,利用A*算法帮助机械臂跳出极值:假设存在一个空间位置P0,在该位置机械臂运行轨迹进入极值,把P0看作是A*算法规划路径的起始位置,通过自适应计算后得出的临时目标Pgoat看作轨迹终点。(θi-λ,θi,θi+λ)是A*算法的搜索空间。假设Pn是第n步机械臂空间构型,Pbest(n)是第n步最好的一个搜索空间的构型。
A*算法的实际花费g(n)为:
(1)
式中:c为机械臂关节变量;Pm为第m步机械臂空间构型,m=1,2,…,n。采用度量法计算估计花费h(n):
h(n)=max[d(Pn,Pgoat)]
(2)
式中:d()为欧氏距离。
将搜索获得的路径信息保存在所构建Open表与Close表中,这两个表分别保存待查空间构型与无需再查空间构型。采用A*算法改进后的人工势场法计算步骤如下:
1)机械臂从P0开始搜索,在Open表中添加Pm,并计算该构型的花费。按照步长在关节空间中遍历邻近P0的构型,在Open表中记录没有出现碰撞的构型,表明当前路径没有障碍物。反之,如果出现碰撞的构型,将P0视为邻近构型前驱,在Close表中添加Pm-1,同时在Open表中删除Pm。
2)遍历Open表,探索出没有发生碰撞且最小总花费的空间构型,设置Pbest(n)成第n步最佳构型。同样在Close表中添加Pbest(n),Open表中删除Pbest(n)。
3)检验临时目标点Pgoat与Pbest(n)是否一致,倘若一致,表示使用A*算法能够帮助机械臂修正避障路径;如果不一致,按照步长继续搜索邻近构型。检测全部构型是否发生碰撞,将未发生碰撞的构型记录为Pson(n)。如果Pson(n)不在Open表中,则添加至Open表,同时跳转到步骤5),否则跳转至步骤4)。
4)假设Open表中已有Pson(n),该构型之前的实际花费g(n)删除,并计算Pbest(n)至该构型的实际花费gnew。比较两次花费,如果g(n)比gnew大,表示Pbest(n)至Pson(n)花费少,因此修改Pbest(n)作为Pson(n)的前驱;假如g(n)比gnew小,则不作处理。
5)计算保存在Open表中的所有构型的实际花费g(n),跳转至步骤2)。如果在Open表中能搜索到临时目标点Pgoat,说明已经找出路径。依照前驱后继关系在Close表中搜索原始构型Pn,确定该路径是起始于空间位置P0、以临时目标点Pgest作为终点的机械臂避障修正最佳路径。
2 虚拟仿真分析
本文所研究的机械臂由沧州伟鹏机器人科技有限公司生产,使用数控智能全自动化技术,发生故障的概率较低,操作方式较为简单,生产原材料严格挑选,不易出现生锈情况,细节设计严格。安装过程中使用支架式或者壁挂式,具有较高的稳定性,相关尺寸参数如图1所示。本文在三维场景中验证避障路径规划的效果,为达到高质量的可视化虚拟仿真效果,使用MATHEMATICA仿真软件开展模拟实验,该仿真软件的视觉效果好,构建模型时效率高。在仿真软件中使用椭圆球模拟障碍物,将椭圆球的中心点看作障碍物的中心点。实验共模拟两种障碍物环境,使用仿真软件模拟机械臂的形态。在仿真软件中设定实验所需要的参数:1)障碍物1坐标(2.5,-1.3,1.3),障碍物2坐标(1.6,0.6,1.8),单位mm;2)搜索步长为0.06 rad,最大遍历次数为360;3)引力、斥力比例参数分别为35、25;4)斥力作用半径为1 mm;5)原始关节角与目标关节角的坐标分别为(-1.2,0.7,1.1,-0.1,0.5,1.3)、(1.5,0.5,1.3,1.4,1.2,1.0),单位rad。
在仿真软件中同时使用未经优化的人工势场法与本文方法规划机械臂避障修正路径,两种方法路径搜索时关节角的变化趋势如图4所示。

图4 路径搜索坐标变化
由图4(a)可知,关节角最终位置为(0.5,0,1.25,-1.05,-1.0,1.3),与目标关节角(1.5,0.5,1.3,1.4,1.2,1.0)差距较大,不属于目标有效范围。由此可以看出,单独使用人工势场法修正机械臂避障路径容易陷入局部极值,造成路径规划无法到达最终目标。由图4(b)可知,遍历360次后,到达目标关节角位置,即到达目标构型位置,说明修正避障路径达到实验目标。从图4中还可看出,关节角θ4和θ5在遍历中间阶段出现明显局部极值,但是θ4在遍历320次后跳出极值,θ5在遍历200次后跳出极值,继续向目标点运动,最终到达目标位置。由此可以看出,使用改进后的人工势场法能够摆脱极值约束,获得最优避障修正路径。
在仿真平台中模拟机械臂避障修正路径,虚拟仿真结果如图5所示。

图5 机械臂避障修正路径
由图5可知,机械臂能够准确避开仿真平台上设定的障碍物,按照改进人工势场法规划后的避障路径开展工作,在完成既定工作的同时,有效躲避障碍物的干扰,通过该虚拟仿真实验能够明显看出该避障修正路径的优势。
将本文方法应用于实际机械臂工作中,通过实验,验证机械臂避障修正效果,结果如图6所示。

图6 实际应用机械臂避障修正
由图6可知,机械臂能够从初始坐标出发,准确躲避提前设定好的障碍物,按照本文方法设定的避障修正路径,到达既定目标点,这一避障修正结果与虚拟仿真结果一致,说明使用本文方法能够准确实现机械臂避障修正。
3 结束语
本文通过研究机械臂抓取避障路径修正方法,利用D-H法构建机械臂坐标系,使用A*算法改进的人工势场法,可避免路径规划时陷入极值,使得机械臂能够及时躲避障碍物按照设定路径到达目标位置,提升避障修正效果。使用MATHEMATICA仿真软件模拟该方法避障路径修正结果,仿真结果显示能够准确躲避工作环境中的多个障碍物,获得良好的工作效果。

