基于Gauss羽流模型低阶预估旋流燃烧室中守恒标量的空间分布*

吴子恒, 张 弛, 张世红, 王柏森

(北京航空航天大学 航空发动机研究院 航空发动机气动热力国家级重点实验室, 北京 102206)

0 引 言

随着先进燃气轮机性能提升,其对燃烧室高效稳定燃烧和高出口温度场品质的需求也在增加[1],对涡轮叶片可靠性与寿命也具有重要意义．燃烧室内复杂的旋流流动和油气混合是影响燃烧高温区和出口温度分布的关键因素,空气通过头部旋流器进入到火焰筒中,与燃料混合燃烧后产生局部高温区,其在旋流作用下在下游发生迁移,影响燃烧室出口温度分布的不均匀性．为了改善燃烧室出口温度场品质,通过头部旋流流动和燃料-空气混合方法来控制旋流燃烧局部高温区的生成具有重要意义．混合分数是表征燃料-空气混合效果的守恒标量[2],其三维空间分布对于燃气轮机燃烧室混合设计具有重要的指导意义．混合分数也是燃烧室湍流燃烧建模的关键参考标量,如概率密度函数输运(PDF)[3]、条件矩(CMC)[4]、层流小火焰等模型[5]通过混合分数构建小尺度混合模型或基于温度、组分与混合分数的关联函数封闭湍流-火焰的相互作用．国内外学者利用非接触光学测量了简单典型燃烧器的混合分数[6-8],然而目前还无法准确测量复杂非典型燃烧器的混合分数场,且通过实验指导燃烧室设计成本高、效率低,测试方案数量有限,参数颗粒度跨度大,对方案的精细化寻优难度极大[9]．燃气轮机燃烧室等复杂燃烧器的混合分数场空间分布往往通过三维数值仿真获得．Kim等[10]采用Reynolds时均(RANS)数值模拟方法探究了不同入口速度和当量比条件下直叶片和扭曲叶片旋流对燃料-空气混合和燃烧特性的影响．Lv等[11]通过大涡模拟(LES)方法研究了燃料-空气混合和分级旋流火焰燃烧稳定性．Steinhausen等[12]消耗了1 800万核时(计算时处理器核心数量乘以小时数),通过直接数值模拟(DNS)的方法,采用详细化学反应机理,研究了湍流火焰-壁面的相互作用．目前三维数值模拟方法广泛应用于燃烧室混合、燃烧高温区、出口温度分布评估和气动设计的过程中,但对于复杂燃烧器,存在算不动、算不起的问题,这对燃烧室方案设计的迭代效率产生很大的影响．低阶预估模型可以规避上述劣势,目前鲜有对于燃烧室混合分数场低阶预估的研究．发展混合分数场的低阶预估模型,以加速燃料-空气混合策略的评估和燃烧室参数化设计过程,具有很高的工程应用价值．

Gauss羽流模型可以用来描述点源在主流来流中的扩散过程[13]．Sánchez-Sosa等[14]将Gauss羽流模型应用于移动机器人室内气体源定位．李万莉[15]将Gauss羽流模型应用到了复杂地形下天然气泄露这一场景,对模型进行了校验．目前,鲜有研究将Gauss羽流模型应用于燃烧室中湍流燃烧混合过程的预测．传统Gauss羽流模型没有考虑径向对流对混合过程的影响,且不能应用于存在旋流来流、多点源和限制域壁面的场景．

本文从混合分数控制方程出发,同时考虑了标量的对流与扩散,推导出考虑对流影响的Gauss烟团方程,从而得到了考虑对流影响的Gauss羽流模型．进一步考虑了旋流来流和多点源场景,发展了镜像反射模型来模拟壁面-羽流雾相互作用,并引入相关修正来确保质量守恒,将新推导的Gauss羽流模型应用于甲烷旋流燃烧室混合分数场的低阶预测．对甲烷旋流燃烧室开展三维数值仿真计算,获得了数值收敛的混合分数场数据库．采用最小二乘法对模型参数进行优化,在宽范围条件下验证了模型的的预测精度．

1 理 论 模 型

1.1 模型推导

图1所示为点源释放气体在直流空气来流速度U=(u,v,w)条件下、开放空间中的发展示意图,针对该过程开展模型推导,对Gauss羽流模型进行二次发展．点源来流在空气来流输运过程中,守恒标量混合分数ξ的控制方程可以写为

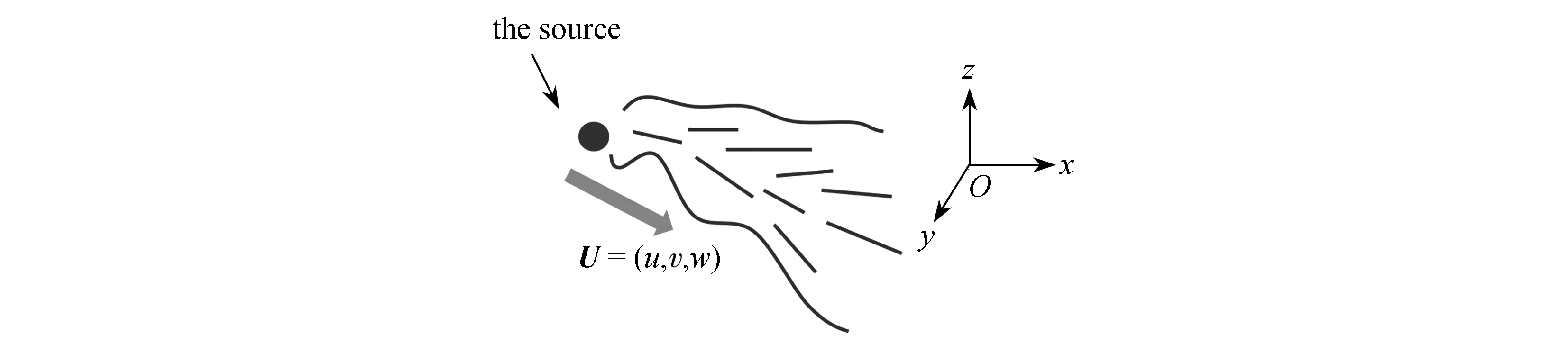
图1 点源释放气体在直流空气来流中的发展示意图Fig. 1 Schematic diagram of the development of a point source releasing gas in a straight air stream

(1)

其中ρ为密度,D为扩散系数[16],在Gauss羽流模型中两者均假设为定值,根据来流工况确定．将ρξ记为C(x,y,z,t),引入三个方向速度分量u,v,w,同样满足Gauss羽流模型假设,u,v,w为定值．式(1)可以写为

(2)

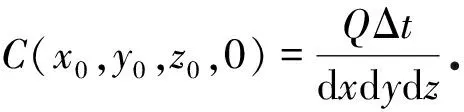
(3)

其中F为Fourier变换,i为虚数单位．

进一步解析式(3)得[18]

(4)

通过Fourier逆变换获得

C(x,y,z,t)=F-1[F(λ1,λ2,λ3,t)]=

(5)

基于式(4),定义函数G(λ1,λ2,λ3,t):

(6)

设函数g(x,y,z,t)的Fourier变换为G(λ1,λ2,λ3,t),即

F[g(x,y,z,t)]=G(λ1,λ2,λ3,t)．

(7)

在t=0 s时刻,上述定义的Fourier变换函数为

F(λ1,λ2,λ3,0)=F[C(x,y,z,0)]．

(8)

根据Fourier卷积定理[19],对于任意函数f和h有

f*h=F-1[F(f)·F(h)]．

(9)

其中*表示卷积运算．

根据式(5)—(9),可以推导获得

C(x,y,z,t)=C(x,y,z,0)*g(x,y,z,t)．

(10)

为获得C(x,y,z,t)的解析式,则需要求解函数g(x,y,z,t):

g(x,y,z,t)=F-1[G(λ1,λ2,λ3,t)]=

(11)

由式(10)和(11)可得

(12)

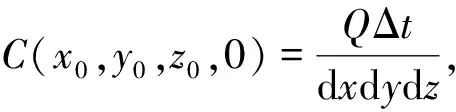
(13)

式(13)便是考虑对流影响的Gauss烟团方程(Gaussian puff equation)．

需要说明的是:式(13)表征点源瞬态释放的气体的空间分布．若要得到式(13)的等效三维稳态方程,即考虑径向对流影响的Gauss羽流模型,可将点源上游来流空间离散为厚度为dx的薄板,并对每个薄板采用Lagrange观点进行分析[21]．图2为将来流离散为薄板扫略点源的示意图．

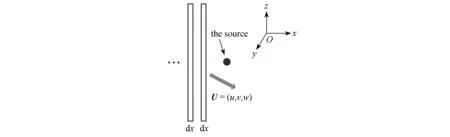
图2 将来流离散为薄板扫略点源的示意图Fig. 2 Schematic diagram of discretizing the flow stream into thin sheets sweeping the point source

参考式(2),离散薄板上的二维输运方程为

(14)

参考式(3)—(13)的推导过程可得到

(15)

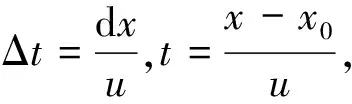
(16)

式(16)可表征不同轴向位置薄板上的浓度分布．每个薄板厚度为dx,将式(16)除以dx,即可得到三维稳态空间分布,即考虑径向对流的Gauss羽流模型

(17)

Gauss羽流模型的有效范围为x轴下游x≥x0．基于C=ρξ,同时考虑点源处混合分数ξ上限为1,将式(17)进一步变换为

(18)

其中a,b为待定模型参数．

如图3所示,当考虑旋流来流的影响时,该点源位置y和z方向上的速度分量v和w分别记为

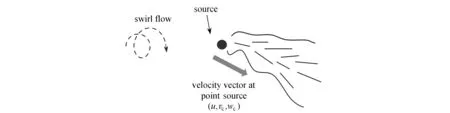
图3 点源释放气体在旋流空气来流中的发展简图Fig. 3 Schematic diagram of the development of a point source releasing gas in a swirling air stream

v=vc,

(19)

w=wc．

(20)

由于燃烧室实际的燃烧室燃料喷射方式存在一个喷嘴具有多个燃料喷射点的情况,因此需要发展多点源模型,以图4所示三点源为例．通过“像源法”[15]建模,引入镜像羽流(mirror-image plume)[21]对应的虚拟等效“点源”,对壁面-羽流相互作用建模．

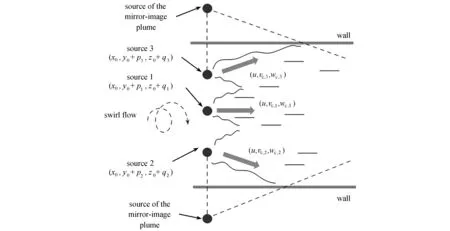
图4 多点源释放气体在旋流空气来流中的发展和镜像反射模型示意图Fig. 4 Schematic diagram of the development of multi-point sources releasing gas in a swirling air stream and the mirror reflection model

若引入N个点源,则点源k处y和z方向上的速度分量分别为

vk=vc,k,

(21)

wk=wc,k．

(22)

由此可获得由多点源表征的混合分数场预估模型

(23)

其中(x0,y0+pk,z0+qk)为点源的位置．引入多点源的同时会产生质量守恒的问题[21],为了模型在预估混合分数场的同时保证质量守恒,并将混合分数限定于0≤ξ(x,y,z)≤1,可将式(23)修正为

(24)

m为待定参数．由于燃烧室限制域的影响,最小混合分数为非0定值,进一步引入燃烧室下游混合分数边界ξfinal,得到

(25)

α,β为待定参数,x′为基于燃烧室长度的无量纲轴向距离．

2 三维数值仿真数据

2.1 模型燃烧室

图5所示为甲烷旋流燃烧室几何结构图,其基于GT2500燃气轮机燃烧室头部旋流方案构建．火焰筒长为345 mm,直径为77 mm,旋流器分内外两级,内旋流叶片角度和数目分别为35°和12,旋流数为0.8．外旋流叶片角度和数目分别为30°和18,旋流数为0.6．喷嘴前端有喷孔24个,每个喷孔直径为2 mm．表1所示为燃烧室工况条件,进口压力为1 554 800 Pa,进口空气流量为0.625 kg/s,通过改变燃料流量来改变燃烧室当量比．分别在燃烧室当量比为0.8,0.9,1.0,1.1的工况下(class 1)开展Reynolds平均计算,获得三维数值仿真数据库,校验模型参数并验证模型准确性;在当量比为0.7,0.75,1.2三个外推工况条件下(class 2)验证模型的宽范围适用性．

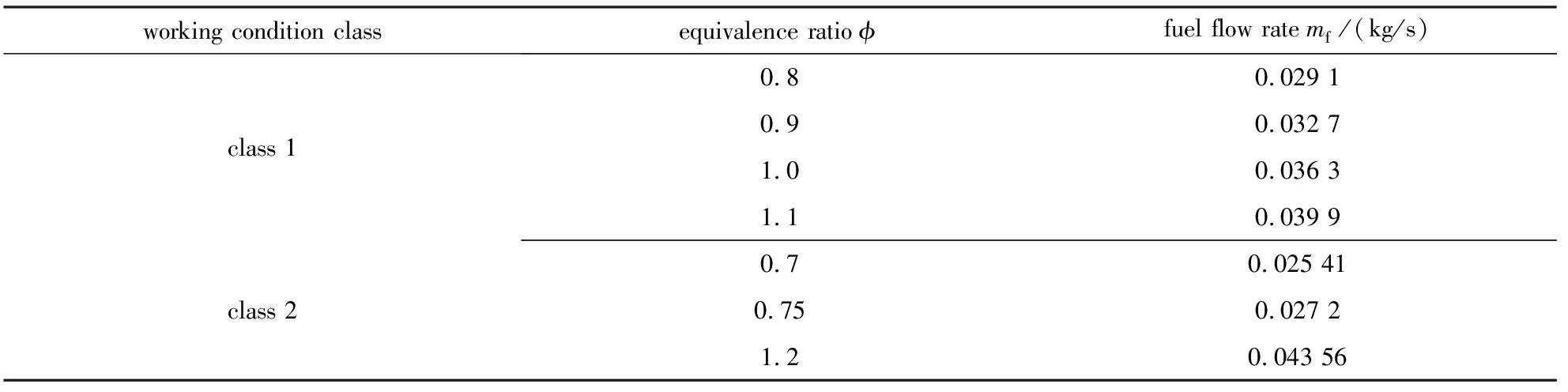
表1 工况条件

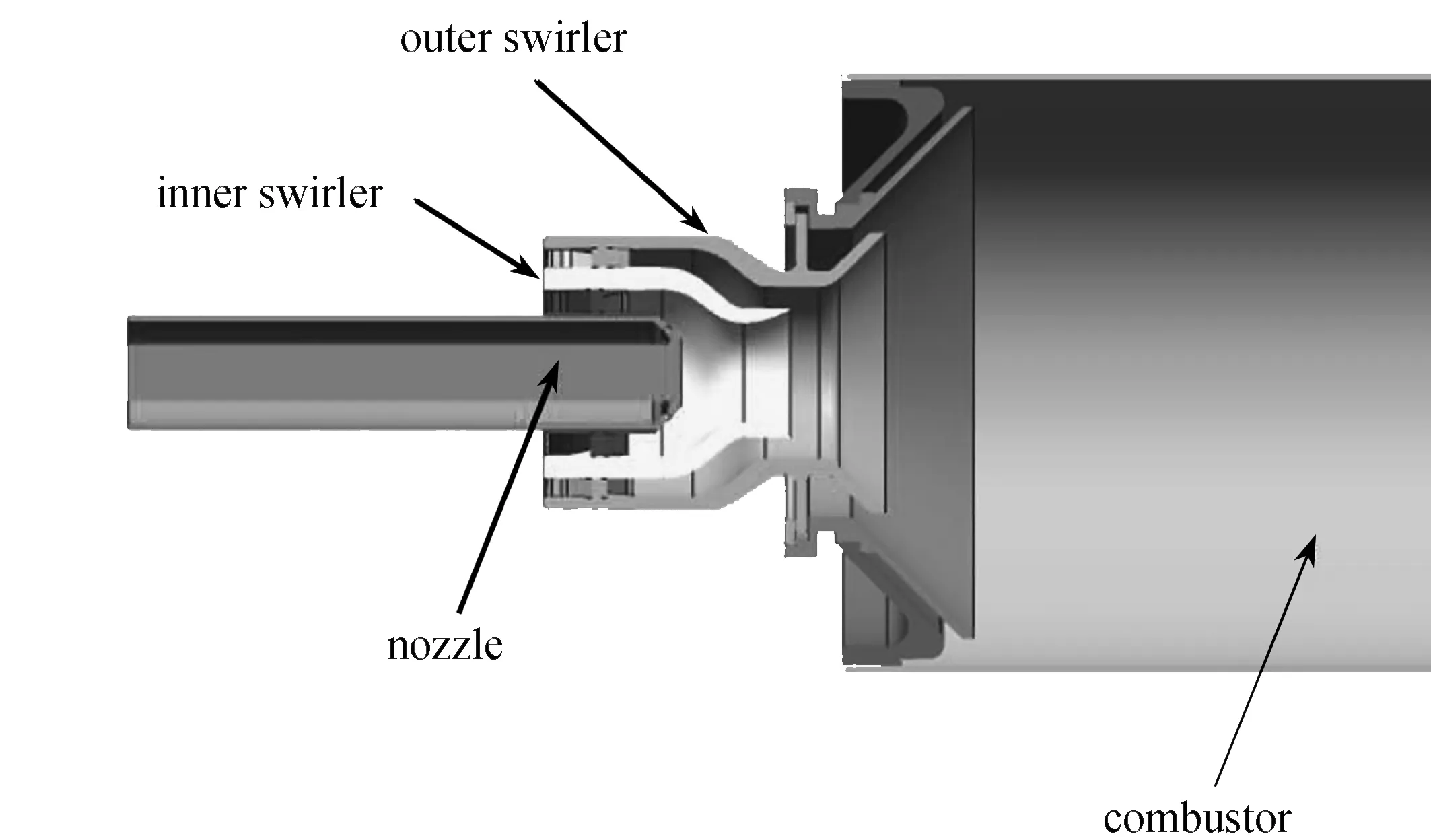
图5 甲烷旋流燃烧室几何结构Fig. 5 The configuration of the methane swirl combustor

在三维数值仿真中[22],采用realizablek-ε模型来描述带旋流特征的湍流流动,壁面处湍流通过可伸缩壁面函数实现,同时采用壁面绝热、无滑移假设．燃烧室进口空气速度脉动和喷嘴出口速度脉动设置为平均速度的5%,密度通过理想气体状态方程求解,黏度值计算遵循Sutherland定律,分别定义Schmidt数和Prandtl数将浓度和温度扩散系数与气体黏度关联．湍流燃烧模型采用FGM(flamelet generated manifold)模型,化学反应机理为GRI3.0,压力-速度耦合算法采用SIMPLE算法．采用有限体积法求解,离散精度为二阶．

2.2 网格无关性验证

针对上述燃烧室流体域,分别生成了384万、520万、890万和1 153万四套离散网格．在当量比φ为1.1的工况下开展计算,取燃烧室中轴线上的CH4质量分数进行网格无关性验证,如图6所示．从图中可以看出,当网格数量大于890万时,燃烧室轴线上CH4质量分数分布不再发生改变,满足网格无关性的基本要求．因此选用890万的网格生成三维数值仿真数据,作为低阶模型的验证依据．

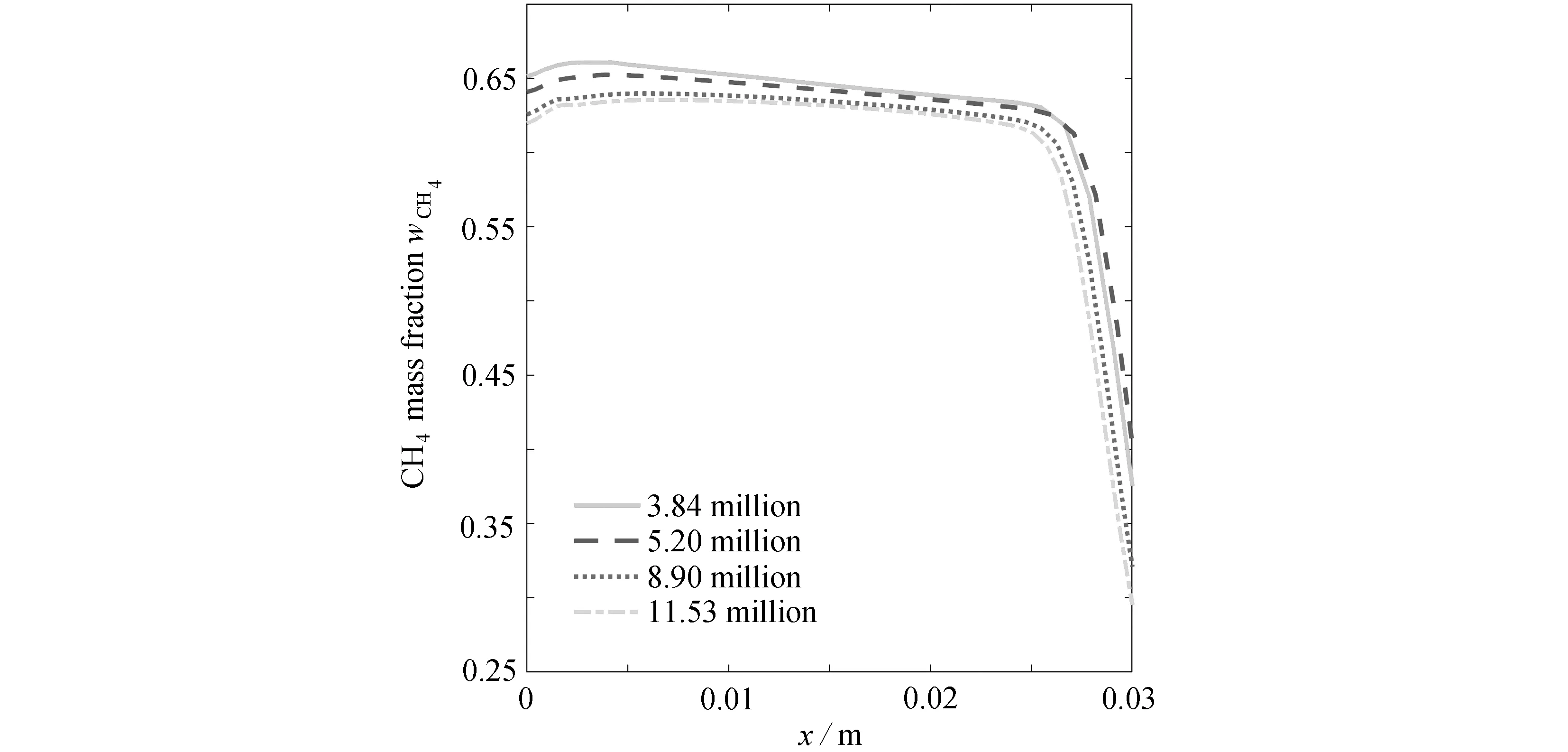
图6 中轴线上甲烷质量分数的分布Fig. 6 Mass fractions of CH4 on the centerline of the axial direction

3 模 型 验 证

3.1 点源数量选取

从低阶预估模型的推导过程看,点源数量与喷嘴的喷射点数量有一定关联,此外考虑壁面反射的影响,通过镜面反射模型引入虚拟等效“点源”．为了保证混合分数场的预估精度,点源数量可能需要大于等于喷嘴实际喷射点的数量．为进一步测试点源数量对预估结果的敏感性,以当量比1.1的工况为例,分别设置点源数量为N=12,24,36开展预估模型的测试,并选取轴向距离x=30 mm和x=60 mm的低阶预估与三维数值仿真云图对比,如图7和图8所示．在x=30 mm处,N=12,24,36的预测结果差异不大．随着轴向距离增大,如在x=60 mm处,N=12导致模型预测的混合分数场出现不平滑、“失真”的现象,而N=24和36的结果基本一致,可以看到混合分数较高的区域均为光滑的同心圆,与CFD结果相符．

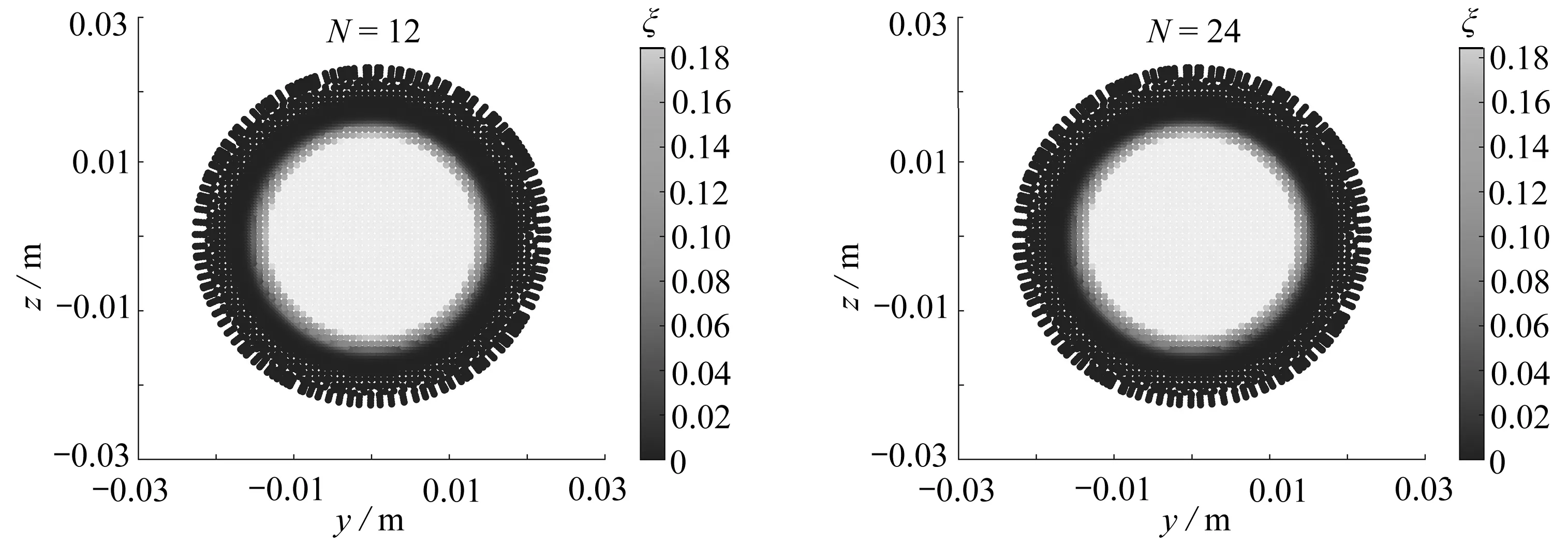
(a) 混合分数模型预估结果(N=12) (b) 混合分数模型预估结果(N=24)(a) Model results of the mixture fraction(N=12)(b) Model results of the mixture fraction(N=24)

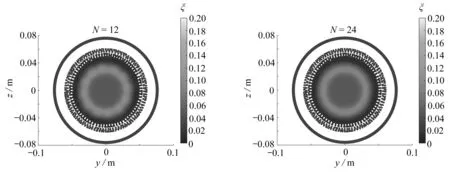
(a) 混合分数模型预估结果(N=12)(b) 混合分数模型预估结果(N=24)(a) Model results of the mixture fraction(N=12)(b) Model results of the mixture fraction(N=24)

如图9所示,取x=60 mm处的径向分布曲线,对不同N的预估结果进行定量比较,N=24和36的预估结果几乎一致,与N=12的结果略有差异．综上所述,将点源数量N=24应用于该案例的模型验证是合理的．

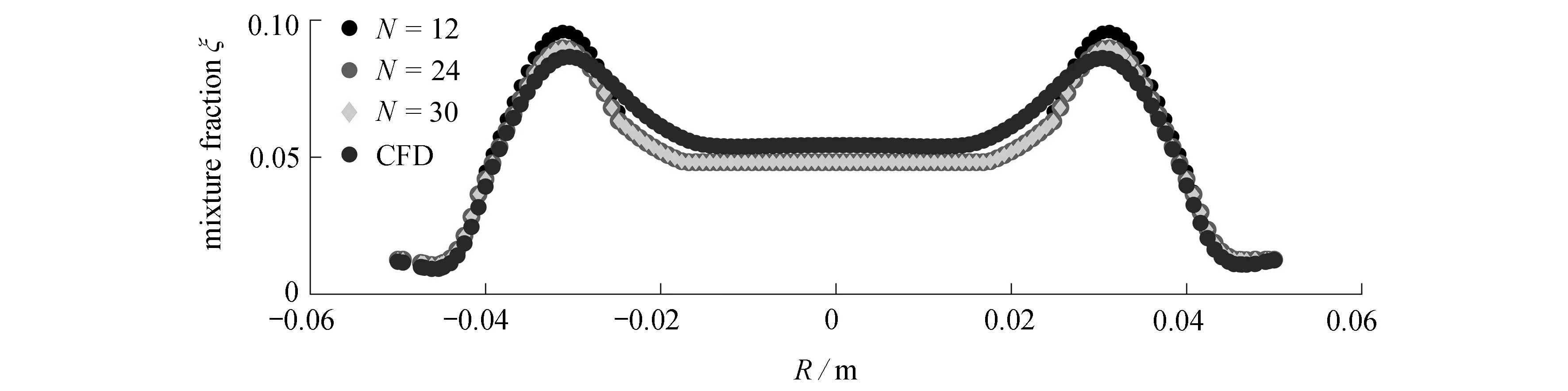
图9 不同点源数量的低阶模型预估结果与三维数值模拟结果对比 (x=60 mm,径向分布, N=12, N=24, N=36)Fig. 9 Comparison of low-order model prediction results of different numbers of point sources and the 3D numerical simulation results (x=60 mm, radial distribution,N=12, N=24, N=36)

3.2 参数寻优以及确定

将式(25)中的N取为24,根据当量比0.8,0.9,1.0,1.1四个工况的混合分数场,使用最小二乘法对模型的参数进行寻优,确定的参数α,β,a,b,m,vc,k,wc,k,pk,qk的取值见附录．

3.3 预估结果与三维数值模拟结果对比分析

3.3.1 参考工况对比分析

取中截面云图,将模型的预估结果与对应的三维数值模拟结果进行对比,如图10所示．模型预估的云图与CFD结果具有一致性,混合分数从喷嘴开始向下游沿着头部壁面不断减小直至消失,整体呈“V”形区域,下游回流区同一轴向位置混合分数最高点不在中轴线上．本文发展的低阶模型考虑旋流来流和径向对流的影响,可以较好地预测上述特征．

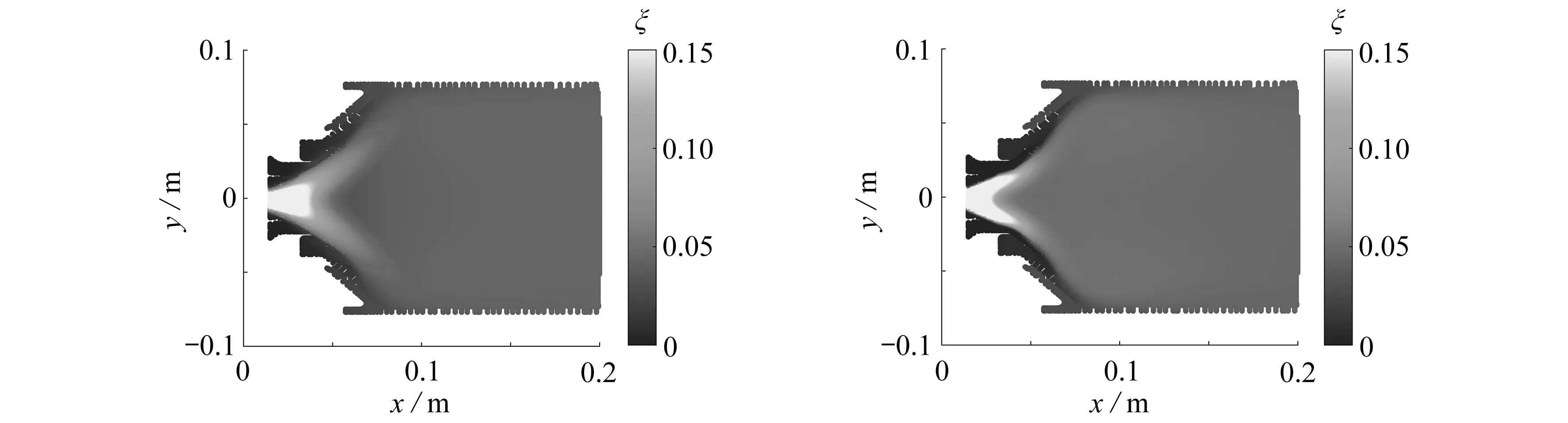
(a) 中截面混合分数低阶模型预估结果(φ=0.8)(b) 中截面混合分数CFD计算结果(φ=0.8) (a) Model results of the mixture fraction (b) CFD results of the mixture fraction at the central plane (φ=0.8) at the central plane (φ=0.8)

将模型预估与三维数值模拟结果进行定量对比,如图11所示．从结果中可以看出,低阶模型可以准确预估混合分数沿中轴线的分布,混合分数在x<0.05 m的区域迅速降低,之后基本保持很小的定值不变,且随头部当量比的升高而升高．

(a) 模型与CFD结果对比(φ=0.8)(b) 模型与CFD结果对比(φ=0.9)(a) Comparison of the results from the model and (b) Comparison of the results from the model and the CFD(φ=0.8) the CFD(φ=0.9)

图12所示为x=0.05 m处的混合分数径向分布,模型的计算结果和CFD的计算结果均是中部较低,两侧较高,且随着头部当量比的减小,峰值逐渐增大,径向边界值逐渐降低．

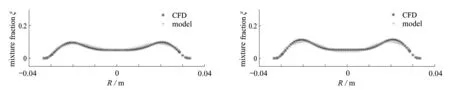
(a) 模型与CFD结果对比(φ=0.8)(b) 模型与CFD结果对比(φ=0.9)(a) Comparison of the results from the model and (b) Comparison of the results from the model and the CFD(φ=0.8) the CFD(φ=0.9)

同样由于低阶模型考虑了旋流来流对标量迁移的影响,模型可以准确地预估径向混合分数“双峰”和“低谷”值及其所在位置．

3.3.2 外推工况对比分析

在参考工况下将预估模型的参数进行校验,并与三维数值模拟结果对比分析后,为验证宽范围下模型的预测精度,对当量比为0.7,0.75,1.2的数据开展验证分析．如图13所示,预估模型依然可以获得混合分数场的“V”形分布特征．图14和图15轴向和径向混合分数变化趋势可以被预估模型准确捕捉．与参考工况相比,模型预估误差和最大误差的位置相似,并对定量对比数据进行分析,模型的预估结果和三维数值仿真结果的平均误差为11.19%．

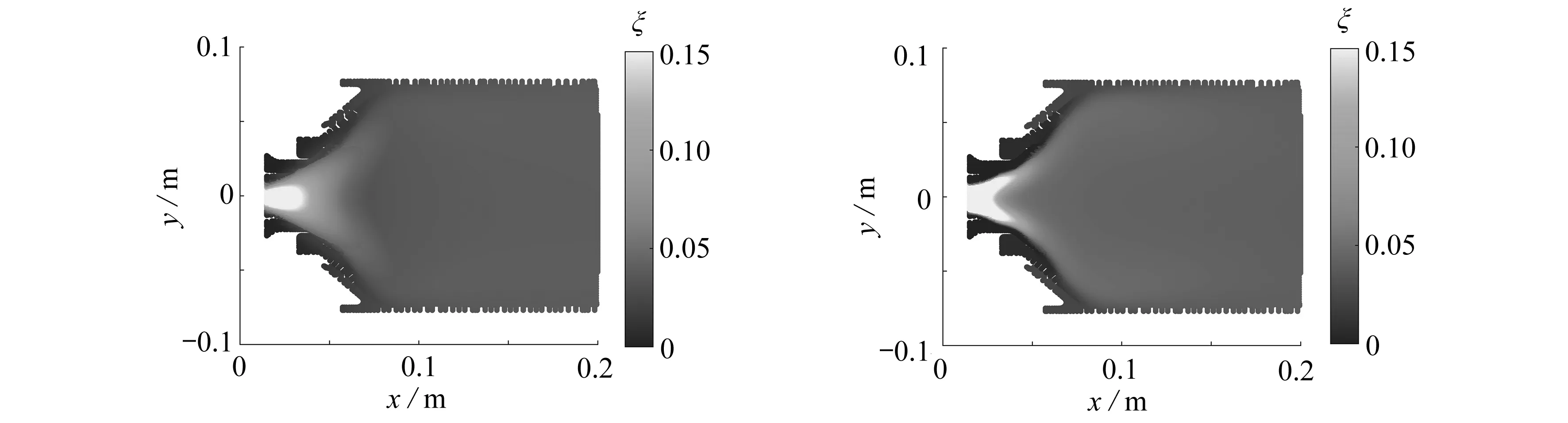
(a) 中截面混合分数模型计算结果(φ=0.7) (b) 中截面混合分数CFD计算结果(φ=0.7)(a) Model results of the mixture fraction (b) CFD results of the mixture fraction at the central plane (φ=0.7) at the central plane (φ=0.7)

(a) 模型与CFD结果对比(φ=0.7)(a) Comparison of the results from the model and the CFD (φ=0.7)

3.4 计算效率

图16所示为低阶预估模型与三维数值仿真模型在参数化设计过程中的耗时对比．本研究需要四个工况下的三维数值仿真数据对所发展的低阶预估模型将进行模型参数校验,三维数值仿真每个算例开销为120核并行迭代2 800步,3 h之后结果收敛,之后低阶模型可以应用于外推工况的混合分数场预估,每算例仅耗时1 s,故低阶模型的开销基本由模型校验所需的算例数量决定．若使用三维数值仿真开展参数化研究,计算开销随算例数量呈线性增长．本研究发展的低阶模型可以极大加快混合分数的计算效率,加快燃烧室混合方案评估和参数化研究．

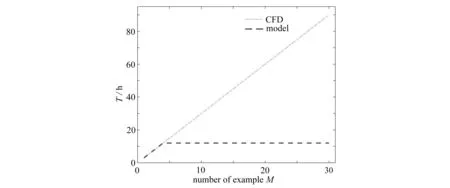
图16 两种方法耗时随算例个数的对比Fig. 16 Comparison of the computational time costs with the number of cases

3.5 低阶预估模型误差

为了更好地评估模型误差,我们将模型外推应用于DLR旋流燃烧室混合分数场预估[23]．如图17所示,与高精度实验数据(experiment)进行定量比对,低阶预估模型(model)的平均误差为10.02%,且低阶模型预估与三维数值仿真(CFD)预测[23]效果相当．综上所述,该低阶预估模型在追求效率的同时,仍然具有较好的预测精度,符合工程应用的需求．

4 结论与展望

1) 本研究对传统的Gauss羽流模型进行了二次开发,考虑了径向对流、旋流来流和壁面的影响,建立了能够应用于甲烷旋流燃烧室的混合分数场低阶预估模型．

2) 基于模型燃烧室当量比0.8,0.9,1.0,1.1四个工况的三维数值模拟数据库,通过最小二乘法对低阶预估模型开展参数寻优,验证了混合分数场的预估精度,在外推工况条件下验证了模型的适用性．

3) 由于最小二乘法对于初值的敏感性, 且容易陷入局部最优解, 会影响混合分数场局部细节的预测, 接下来可以发展更精确的模型参数寻优方法[24],进一步增强模型的宽适用性及其在燃烧室设计应用时的鲁棒性．

附 录

参数α,β,a,b,m的值如表A1所示．

表A1 参数α,β,a,b,m的值

参数vc,k,wc,k,pk,qk的值如表A2—A5所示．

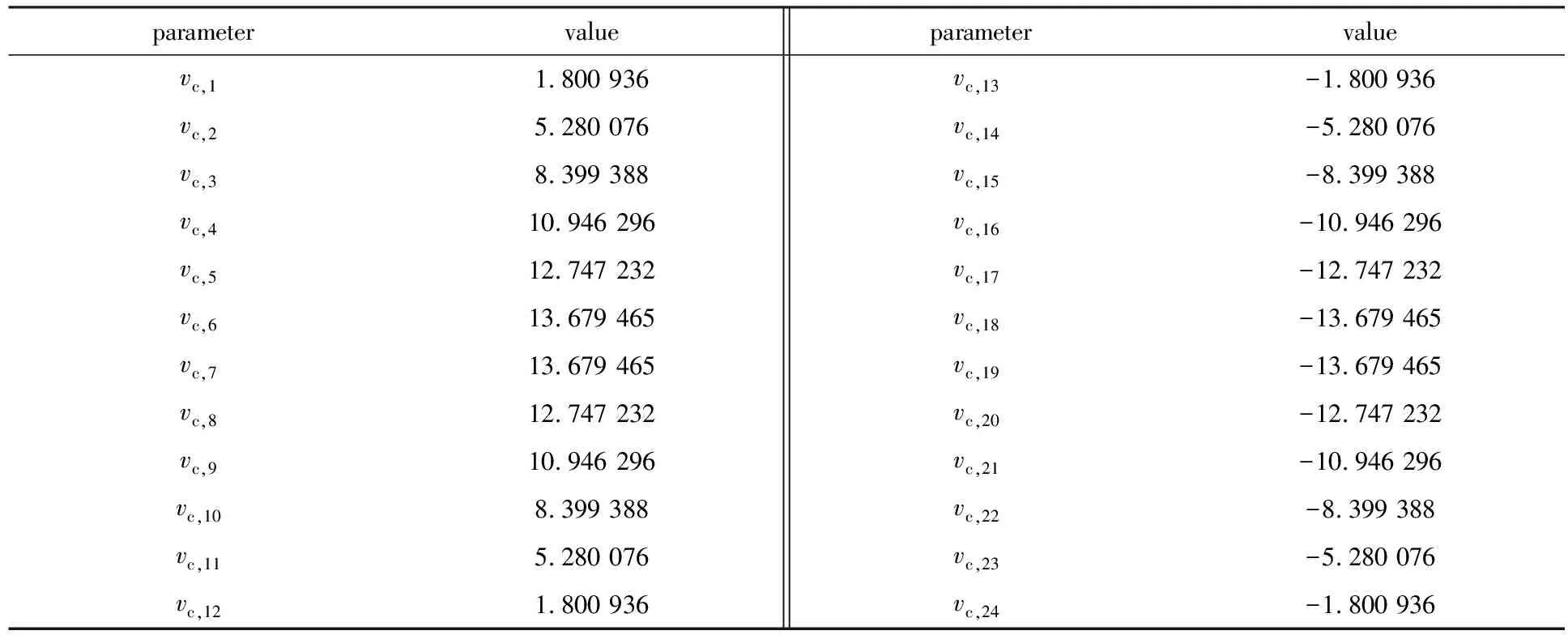
表A2 参数vc,k的值

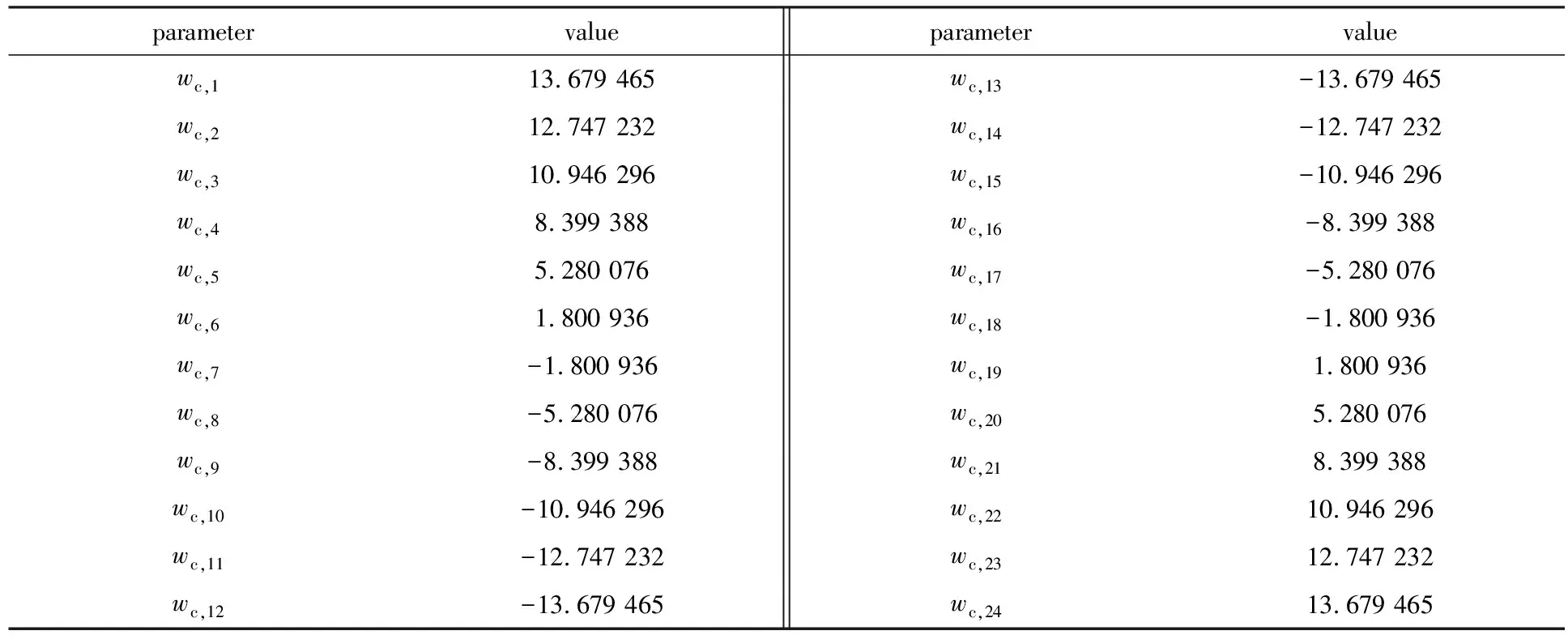
表A3 参数wc,k的值

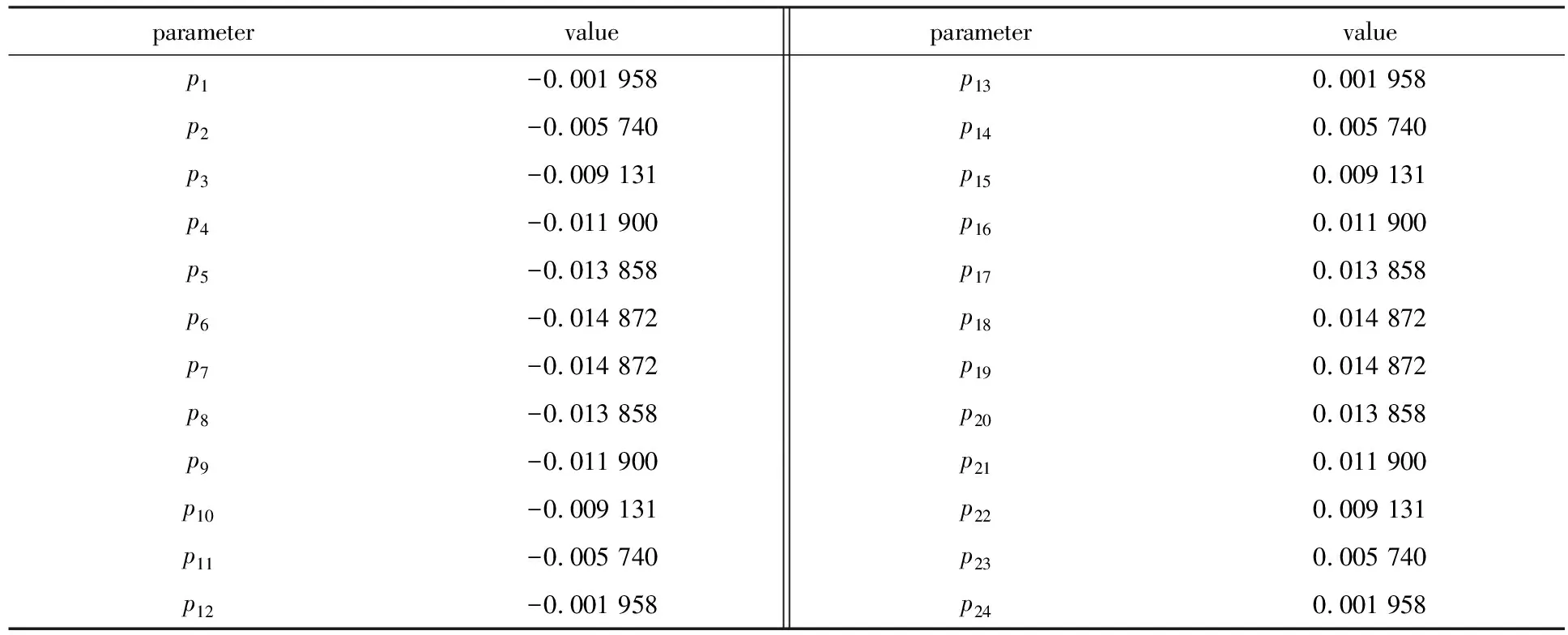
表A4 参数pk的值

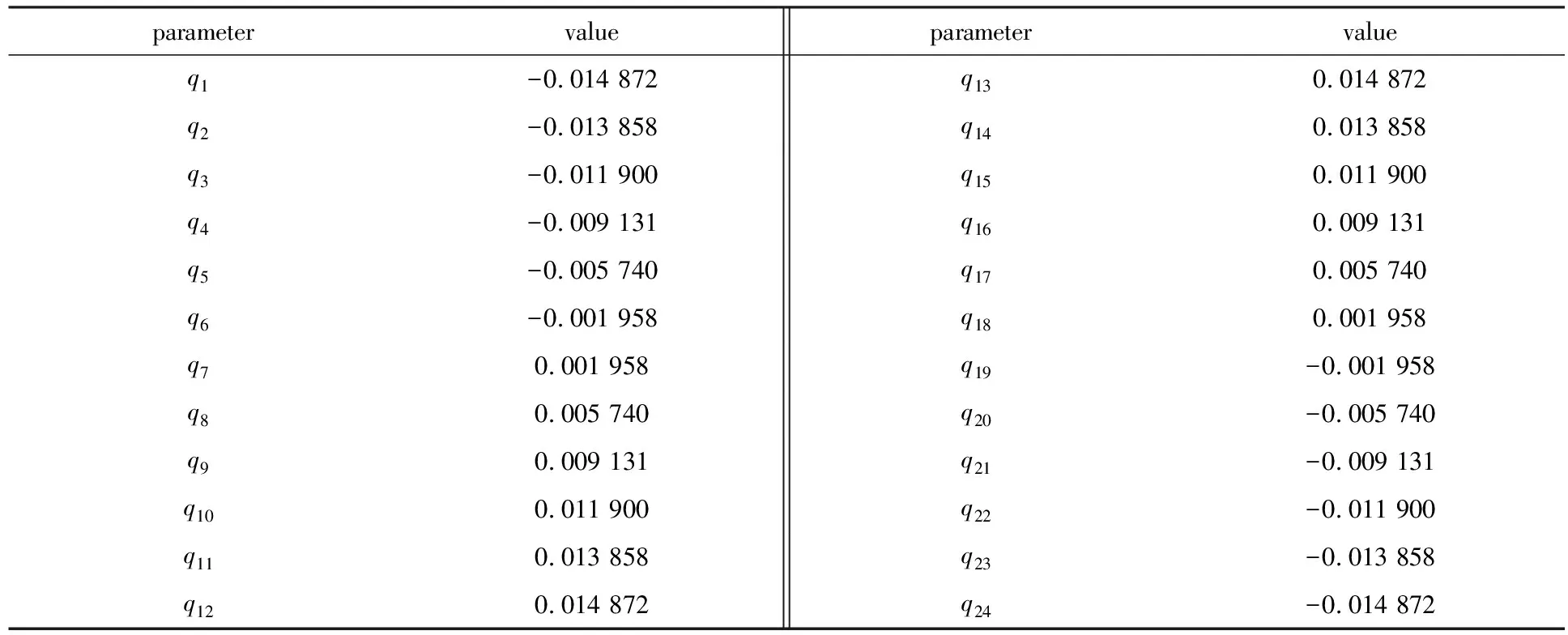
表A5 参数qk的值